110 Stability of Genetic Oscillators with Distributed Delayed Feedback

ABSTRACT

Genetic oscillators govern periodic phenomena in biology including circadian rhythms and are also the basis of biological clocks used in the design of synthetic genetic circuits. Models of genetic oscillators tend to neglect biological detail, however, because biological systems tend to be too complicated to model efficiently. One way to incorporate additional biological detail into models of genetic oscillators is to use distributed delay differential equations. To investigate the utility of distributed delay differential equations for modeling genetic oscillators, we constructed delayed differential equation models of genetic oscilla- tory motifs. We found that these models are equivalent to higher-dimension models, which are reflective of more granular biological detail. We also characterized the stability of these models. Our findings may inform future modeling efforts in the domains of synthetic and systems biology, where delayed differential equations could pose advantages over ordinary differential equation models.

INTRODUCTION

Genetic oscillators, which are intrinsic time-keeping devices in living organisms, have been the subject of research in the field of mathematical biology for some time [1, 2]. The study of these oscillators has led to a deeper understanding of the molecular mechanisms that underlie a wide range of biological processes, including circadian rhythms [3], cell cycle regulation [4], and developmental processes [5]. Circadian rhythms, for instance, are endogenous rhythms that persist in the absence of external cues and are responsible for co- ordinating a wide range of physiological and behavioral processes [6]. Biological clocks, based on the principles of genetic oscillators, have been engineered to regulate the expres- sion of genes in synthetic circuits [7, 8], with applications ranging from biosensors [9] to drug delivery systems [10].

While genetic oscillators have become increasingly well understood, modeling their behavior presents a significant challenge [11]. Mathematical models of genetic oscilla- tors must balance the need for accuracy with computational efficiency, as the large number of molecular interactions involved in these systems can be computationally expensive to model in detail [12]. As a result, models of genetic oscillators tend to simplify the un- derlying biology, often neglecting important biological details in favor of simplicity and efficiency [13, 14]. These simplified models may fail to reflect dynamics observed in vivo by, for example, altering system stability [11].

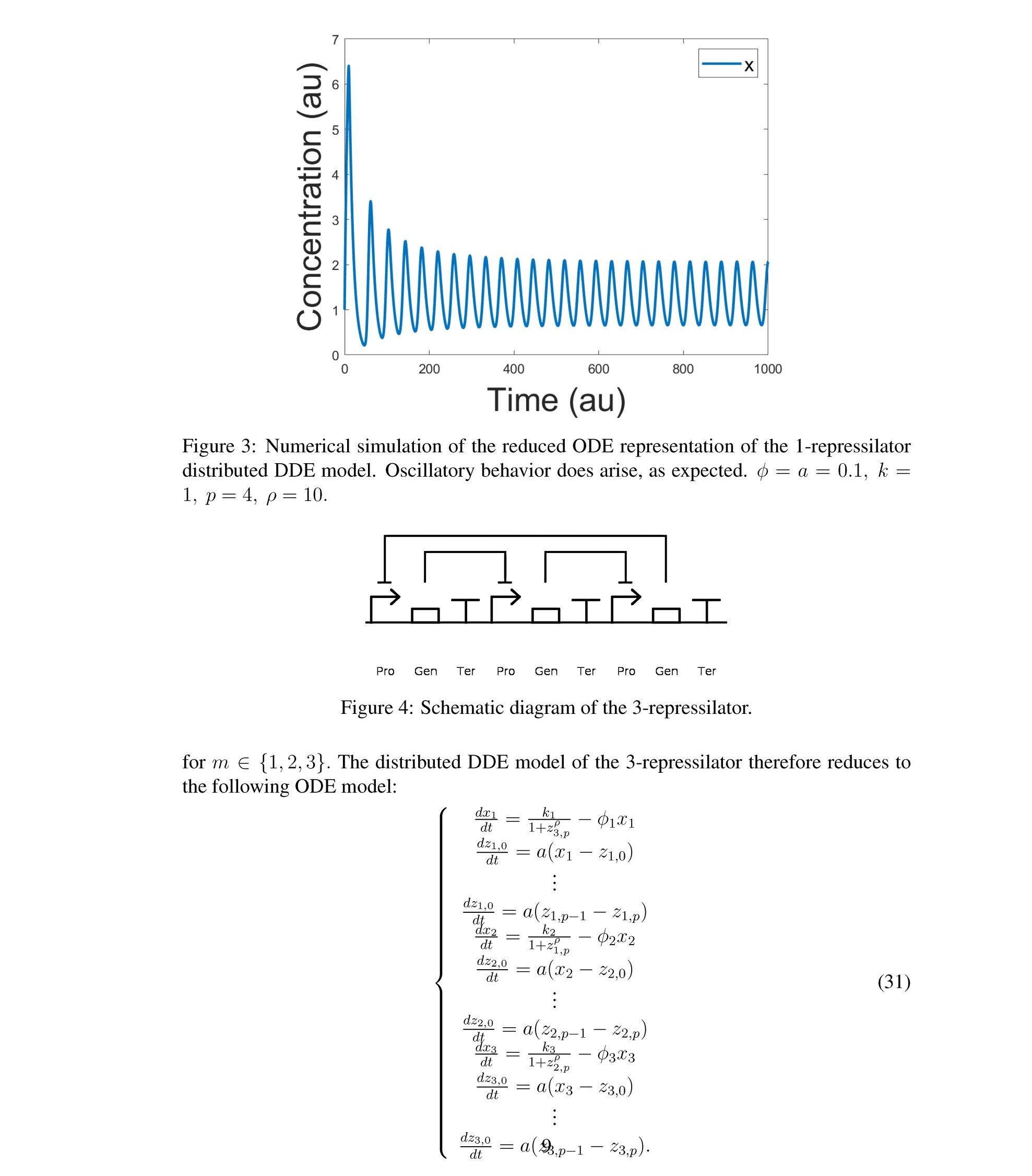
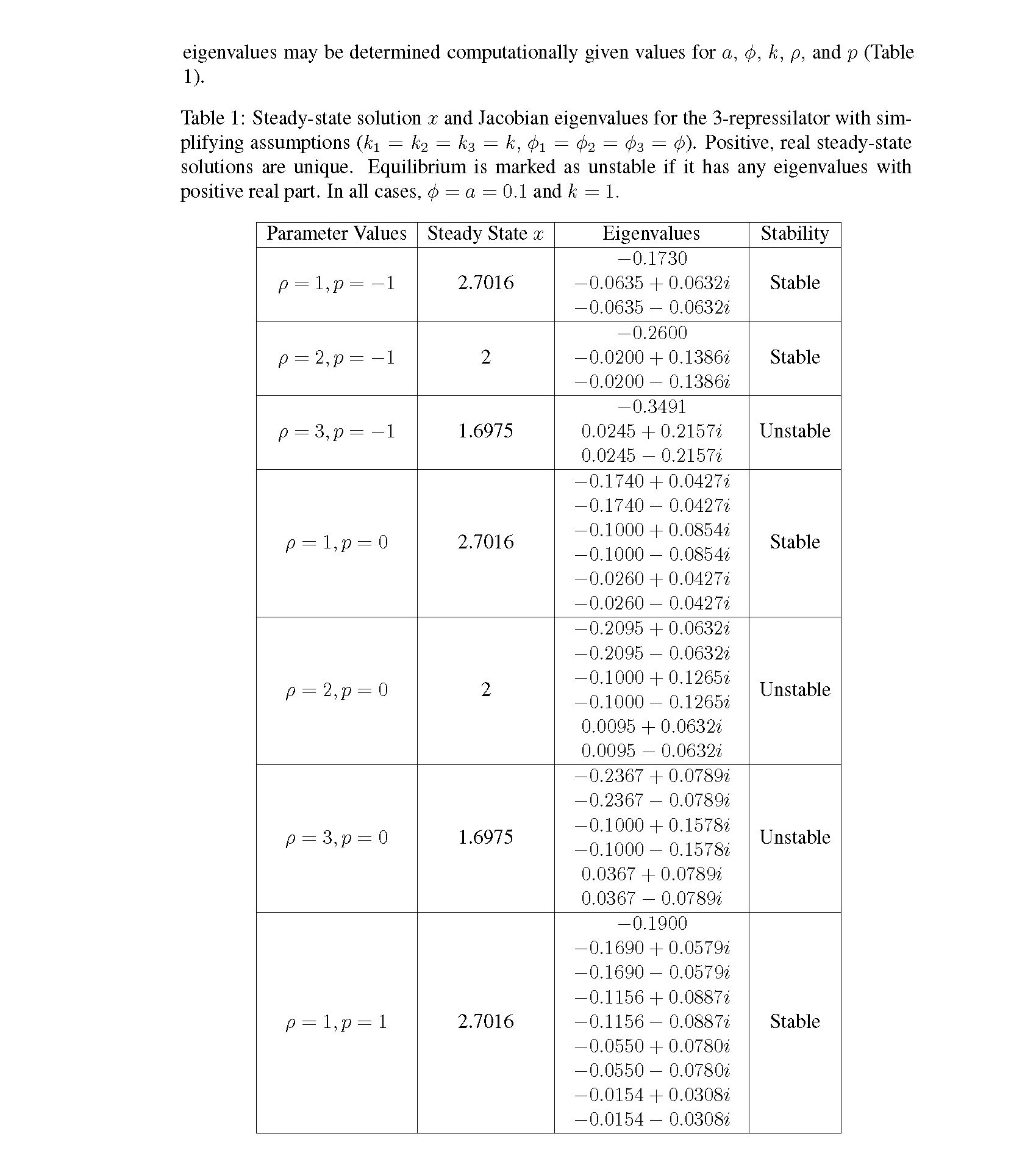
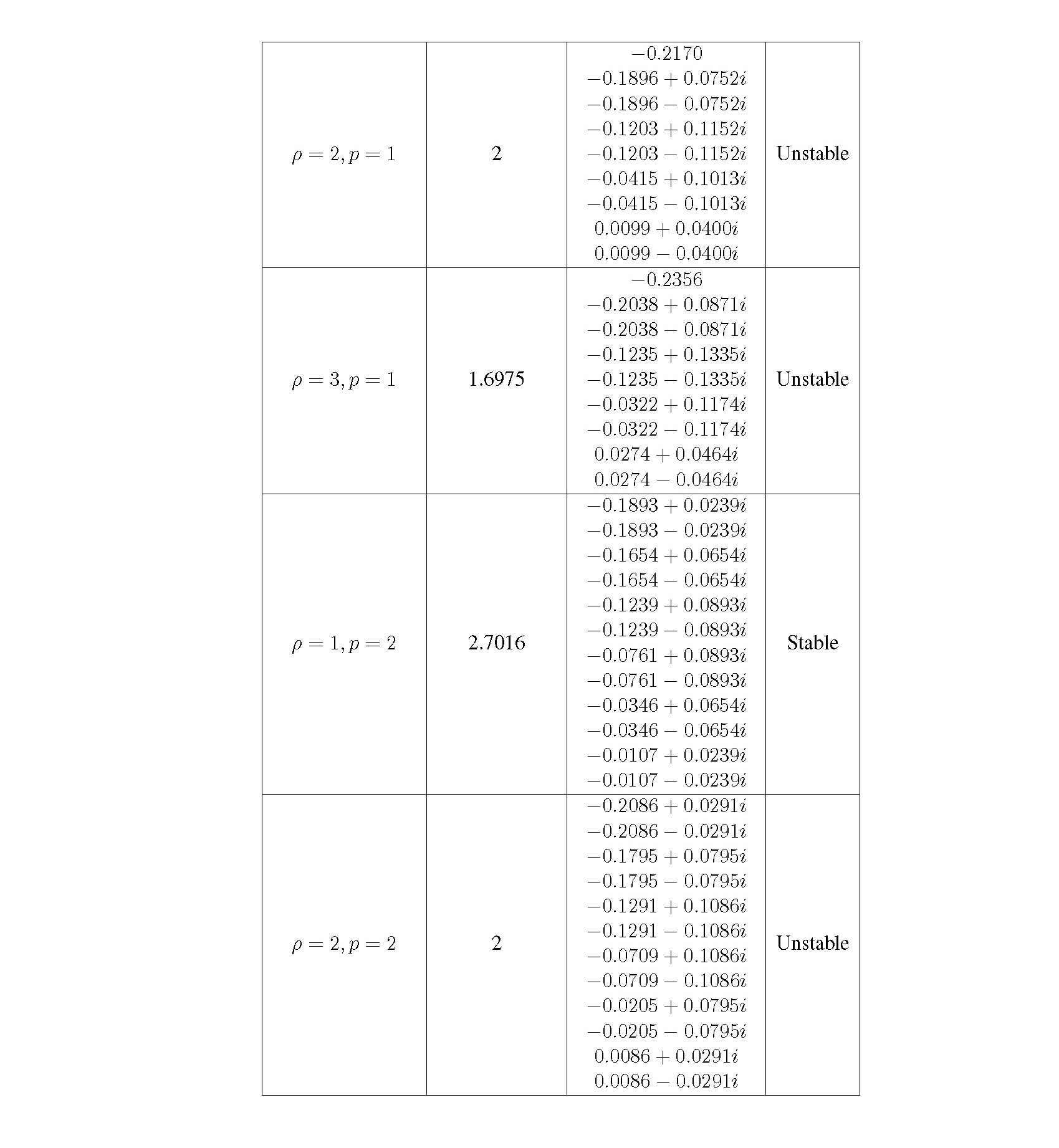
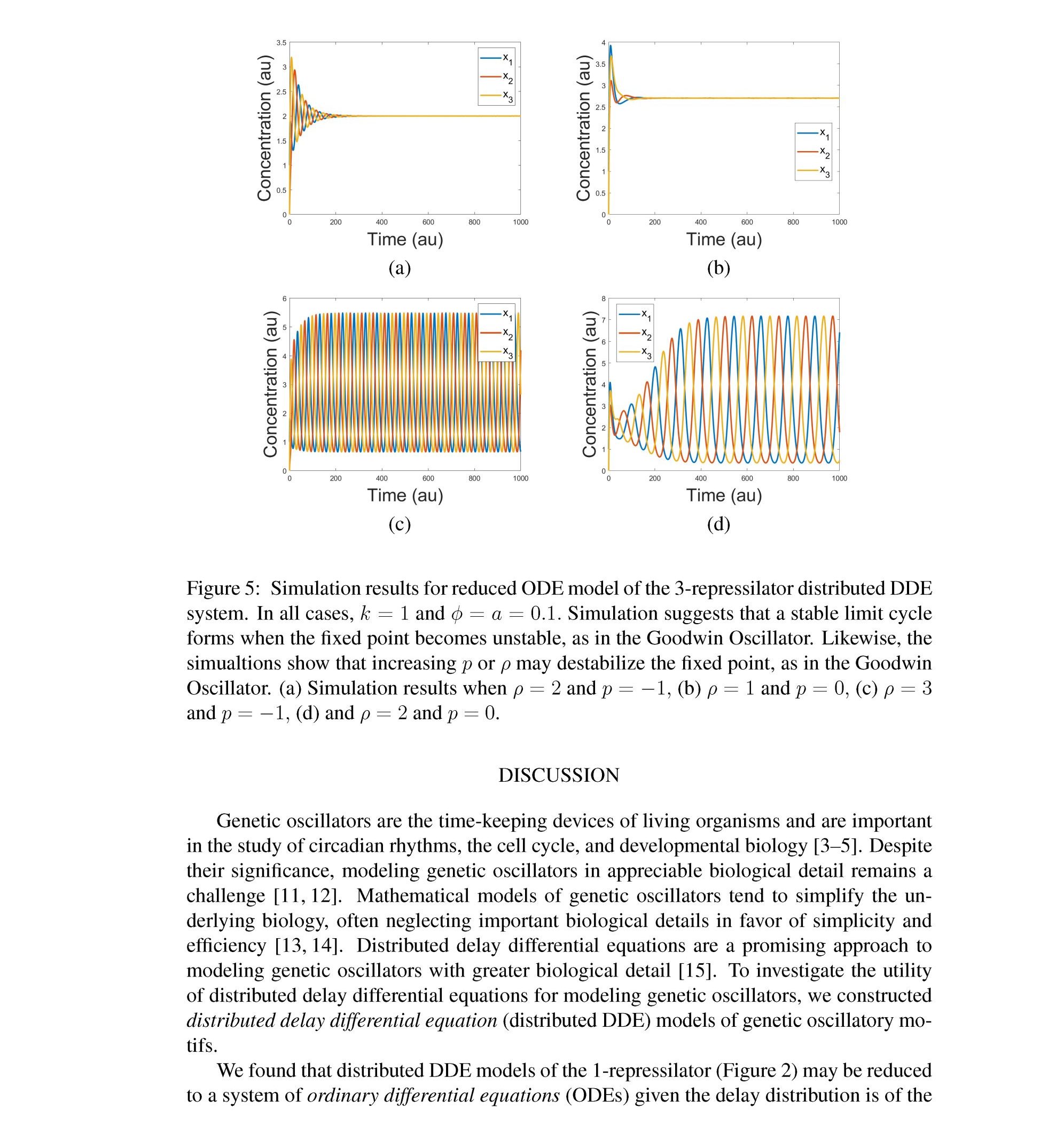
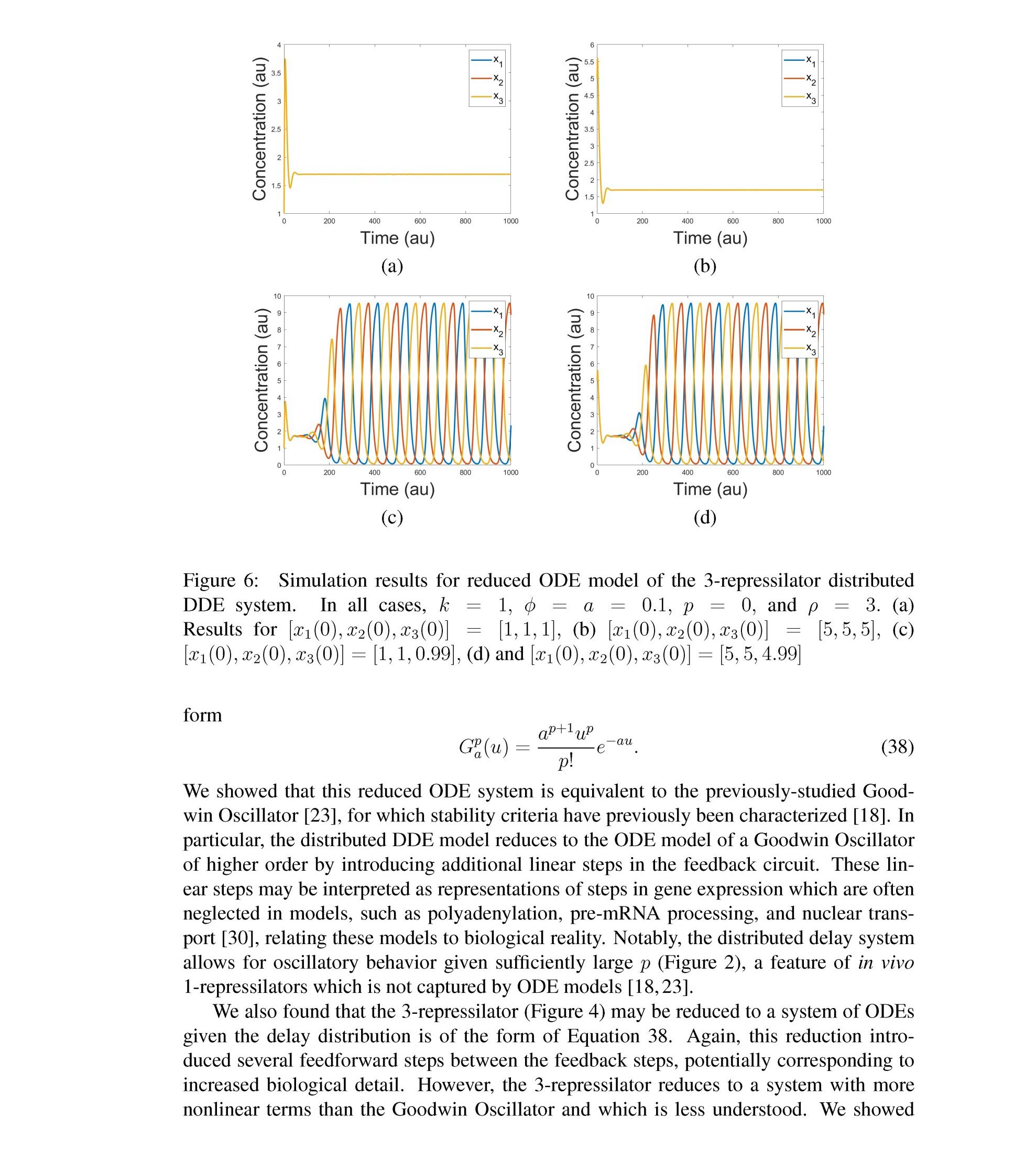
Distributed delay differential equations are a promising approach to modeling genetic oscillators with greater biological detail [15]. Unlike ordinary differential equations which ignore time delays entirely and discrete delay differential equations which assume constant delay in feedback steps [16, 17], distributed delay differential equations allow for a distri- bution of delays that more closely approximates the complex biological interactions that occur in living organisms. These models have been shown to accurately capture the be- havior of some simple genetic oscillators [18], while also remaining intuitive and simple to simulate. To investigate the utility of distributed delay differential equations for model- ing genetic oscillators, we constructed and analyzed distributed delay differential equation models of repressilators, one important class of synthetic genetic oscillator [2, 7].

ACKNOWLEDGEMENTS

We would like to thank Professor Elena Cherkaev at the University of Utah who pro- vided mentorship and expertise throughout this project.

REFERENCES

[1]      Deborah Bell-Pedersen, Vincent M. Cassone, David J. Earnest, Susan S. Golden, Paul E. Hardin, Terry L. Thomas, and Mark J. Zoran. Circadian rhythms from multiple oscillators: Lessons from diverse organisms. Nature Reviews Genetics, 6(7):544–556, 2005.

[2]      Michael B. Elowitz and Stanislas Leibler. A synthetic oscillatory network of tran- scriptional regulators. Nature, 403(6767):335–338, 2000.

[3]      P Smolen and JH Byrne. Circadian rhythm models. Encyclopedia of Neuroscience, pages 957–963, 2009.

[4]      Sean Crosson, Harley McAdams, and Lucy Shapiro. A genetic oscillator and the regulation of cell cycle progression in caulobacter crescentus. Cell Cycle, 3(10):1252– 1254, 2004.

[5]      Charisios Tsiairis and Helge Großhans. Gene expression oscillations in c. elegans underlie a new developmental clock. In Current Topics in Developmental Biology, volume 144, pages 19–43. Elsevier, 2021.

[6]      Martha Hotz Vitaterna, Joseph S Takahashi, and Fred W Turek. Overview of circadian rhythms. Alcohol research & health, 25(2):85, 2001.

[7]      Oliver Purcell, Nigel J Savery, Claire S Grierson, and Mario Di Bernardo. A compar- ative analysis of synthetic genetic oscillators. Journal of The Royal Society Interface, 7(52):1503–1524, 2010.

[8]      Peng-Fei Xia, Hua Ling, Jee Loon Foo, and Matthew Wook Chang. Synthetic ge- netic circuits for programmable biological functionalities. Biotechnology advances, 37(6):107393, 2019.

[9]      Cong Gao, Peng Xu, Chao Ye, Xiulai Chen, and Liming Liu. Genetic circuit-assisted smart microbial engineering. Trends in microbiology, 27(12):1011–1024, 2019.

[10]      Pu Shi, Joshua A Gustafson, and J Andrew MacKay. Genetically engineered nanocar- riers for drug delivery. International journal of nanomedicine, 9:1617–1626, 2014.

[11]      Alexander N Churilov, Alexander Medvedev, and Zhanybai T Zhusubaliyev. Delay- induced dynamical phenomena in impulsive goodwin’s oscillator: What we know so far. In 2015 54th IEEE Conference on Decision and Control (CDC), pages 590–595. IEEE, 2015.

[12]      Michael A Gibson and Jehoshua Bruck. Efficient exact stochastic simulation of chem- ical systems with many species and many channels. The journal of physical chemistry A, 104(9):1876–1889, 2000.

[13]      Payton J Thomas, Mohammad Ahmadi, Hao Zheng, and Chris J Myers. A comparison of weighted stochastic simulation methods. bioRxiv, pages 2021–09, 2021.

[14]      Mohammad Ahmadi, Payton J Thomas, Lukas Buecherl, Chris Winstead, Chris J Myers, and Hao Zheng. A comparison of weighted stochastic simulation methods for the analysis of genetic circuits. ACS Synthetic Biology, 2022.

[15]      Marcella Gomez and Richard M Murray. Delay-based approximations of biological systems for analysis and design. In Am. Contr. Conf., 2012.

[16]      Franco Blanchini and Elisa Franco. Structural analysis of biological networks. A Systems Theoretic Approach to Systems and Synthetic Biology I: Models and System Characterizations, pages 47–71, 2014.

[17]      David S Glass, Xiaofan Jin, and Ingmar H Riedel-Kruse. Nonlinear delay differen- tial equations and their application to modeling biological network motifs. Nature communications, 12(1):1788, 2021.

[18]      N MacDonald. Time lag in a model of a biochemical reaction sequence with end product inhibition. Journal of Theoretical Biology, 67(3):549–556, 1977.

[19]      Marc R Roussel. Delay-differential equations. In Nonlinear Dynamics, 2053-2571, pages 12–1 to 12–14. Morgan Claypool Publishers, 2019.

[20]      Jean-Pierre Richard. Time-delay systems: an overview of some recent advances and open problems. Automatica, 39(10):1667–1694, 2003.

[21]      Philip Doldo and Jamol Pender. A note on the interpretation of distributed delay equations, 2021.

[22]      Luo Albert C J. and Jian-Qiao Sun. Chapter 3: Differential-Delay Equations, page 85–119. Springer Berlin Heidelberg, 2012.

[23]      Brian C. Goodwin. Oscillatory behavior in enzymatic control processes. Advances in Enzyme Regulation, 3:425–437, 1965.

[24]      Rudolf Gesztelyi, Judit Zsuga, Adam Kemeny-Beke, Balazs Varga, Bela Juhasz, and Arpad Tosaki. The hill equation and the origin of quantitative pharmacology. Archive for History of Exact Sciences, 66(4):427–438, 2012.

[25]      Maya Mincheva and Marc R. Roussel. Turing-hopf instability in biochemical reaction networks arising from pairs of subnetworks. Mathematical Biosciences, 240(1):1–11, 2012.