14 Middle School Student-Generated Ideas About Math: Definitions and Utility

Abstract

 This study investigates student-generated ideas about mathematics, focusing specifically on students’ definitions of math and their notions of math’s utility. The study is designed to explore these concepts concurrently through two research questions: (1) How do middle school students define mathematics? (2) How do those definitions connect with or relate to their ideas of math utility? Student-generated ideas are central to this exploration because they offer more insight into what students are learning and how they are motivated to learn (Canning & Harackiewicz, 2015; Eccles & Wigfield, 2002; Johansson & Sumpter, 2020). I focus on middle- school students as they are at a critical period in their educational careers and perceptions of math (Priniski & Thoman, 2020). Students participated in semi-structured interviews, and select questions were chosen for analysis. Findings reveal that most students primarily thought about math content over math processes when offering ideas about defining math. Additionally, there were connections between which areas of math were mentioned in connection with which domains of utility. Among content areas defined by the National Council for Teachers of Mathematics (NCTM), Numbers & Operations and Measurement were most frequently connected to Daily Activities. Among math processes defined by the NCTM, Problem Solving and Connections were most frequently connected to Future Job/Career. However, there was not a connection between the breadth of a student’s math definitions and the breadth of their notions of math’s utility. These findings have implications for what kinds of instructional decisions teachers make in their classrooms, and how they try to connect math content and processes to their students’ personal lives.

IntroductionMany educators like to project the idea that “math is everywhere” to ingrain a sense of its utility in students. Students frequently echoed this idea when asked questions about the usefulness of math (Dobie, 2019a). However, when students are given the opportunity to discuss mathematics, they experience difficulties when making these connections beyond the classroom (McDonough & Sullivan, 2014) or when thoughtfully and meaningfully applying a math concept to a real-world context (Metzger et al., 2019). Thus, students are not finding examples of math’s utility “everywhere.” Students mostly refer to money and future jobs when thinking about math utility (Dobie, 2019b). Existing literature has shown that when students think of math as useful, they are likely to have improved academic achievement and higher personal interest in math, and this can be especially impactful and beneficial for students with lower mathematics performance (Hulleman & Harackiewicz, 2009). However, it is important that researchers understand students’ ideas about utility rather than just asking if students think math is useful (Dobie, 2019b; McDonough & Sullivan, 2015). This difference is important because when students are only given the opportunity to think of usefulness in terms of teachers’ examples, it can be detrimental for students who have a low sense of personal math competence and who have not personally connected with those notions of utility (Hulleman & Harackiewicz, 2009). Additionally, this difference between students’ own ideas of utility and the generalized belief that math is useful is important when considering the scope of ideas represented in research on math utility. The representation of more diverse notions of math utility can lead to more equitable math classrooms (Dobie, 2019b). Thus, there is a need to consider what students’ perspectives may add to knowledge of effective math instruction.

While past studies point to limited perceptions of math utility, other research demonstrates that students may also have limited definitions of math. In one study, student- generated definitions of mathematics from students in grades one through four were limited to numbers, counting, and basic operations, which left out many math domains including algebra, geometry, measurement, and problem solving (Metzger et al., 2019). Other research with students in grades two through eight in elementary and middle school demonstrated that students simply struggle when tasked with defining math (McDonough & Sullivan, 2015).

Emotional responses are tied to conceptions about math, and the emotional experiences of math are shown to become more negative from year to year starting as early as elementary school from grades two to five (Johansson & Sumpter, 2010). Students express more frustration as the math becomes more complex. As a result, elementary students may disengage from expanding their scope of what math is. However, this disengagement is not the choice of students; it is the result of math instruction that teaches them to understand math as something that exists in the classroom, in a book, and at a desk (Johansson & Sumpter, 2010). Interview responses from students showed that students do not associate math learned in school with daily math encounters beyond the classroom (Metzger, et al., 2019). Because math instruction is often abstract and not explicitly tied to these daily encounters, students are not offered channels to make meaningful math connections that would expand their scope and definition of mathematics. Understanding student definitions of math is important for teachers to be responsive to what students already know for effective instruction including making more explicit math connections to real world contexts (McDonough & Sullivan, 2015; Metzger, et al., 2019; Moll et al., 1992).

Both ideas of math utility and definition are important for effective instruction that maintains student motivation. Given that one’s way of defining math is likely to play a role in where one sees math in the world, there is a need to study these concepts concurrently. Studying these concepts through middle school student ideas provides insight into a critical period in students’ formation of their math identities and ideas (Priniski & Thoman, 2020). The current study explores two research questions: (1) How do middle school students define mathematics (2) How do those definitions connect with or relate to their ideas of math utility? Exploring these questions may have implications for how teachers make instructional decisions in math.

Literature Review

The research questions rely on existing literature about students and their ideas about mathematics. First, I consider research about how students construct their own definitions of math and how math is defined by instructional standards. Then, I consider Expectancy-Value Theory to understand how notions of utility are related to students’ learning motivation. Next, we discuss the importance of using student-generated ideas.

Definitions of Math

To explore how students define mathematics, it is important to consider what is involved in the formation of their conceptions. Johansson and Sumpter (2020) define “conception’’ in relation to students: “…an abstract or general idea that may have both affective and cognitive dimensions inferred or derived from specific instances. Hence, students’ conceptions consist of their belief systems, values, and attitudes reflecting their experiences” (Johansson & Sumpter, 2020, p. 78). Establishing this definition allows an open-ended exploration of student ideas as to not limit student-generated ideas, which are essential to the research purpose.

There are multiple aspects to consider with this definition. First, a conception is general in the sense that it is not comprehensive or absolute, and it is dynamic. Second, student ideas or conceptions will involve affective characteristics. These include how they feel about math, what they think math is for, and what they think math looks like. Conceptions also involve cognitive dimensions where students might give more explicit and tangible answers of what math is through examples. Considering these components that make up students’ ideas, teachers and researchers should be mindful that student responses are limited to their personal experiences and perspectives.

Because student conceptions of math are dependent on their own experiences, it is important to consider existing research that focuses on how students imagine themselves in relation to math. Johansson and Sumpter (2020) explored this element in a qualitative analysis by asking students to draw a picture of themselves when they are engaging with math. Second and fifth grade student illustrations led to the same conclusion where students imagined themselves alone and working in a book; this was their image of what it means to do math (Johnasson & Sumpter, 2020). The researchers compared these findings to observations of the students in class. Those observations revealed that these depictions were in line with the kinds of math activities that happened in their classrooms, where students were observed working alone or in small groups and with their textbooks. While this encourages teachers to re-evaluate their instructional strategies in math, it also demonstrates that students’ ideas are clearly reflective of their lived experiences in line with Johansson and Sumpter’s definition of “conception” related to math ideas.

In addition to allowing student responses to incorporate their personal experiences, a thorough analysis of definitions requires mechanisms for coding student ideas to understand them in collection. Metzger and others (2019) provide ways to decipher students’ math definitions using standards from the National Council of Teachers of Mathematics (NCTM) (NCTM, 2000). Using standards that guide teachers’ math instruction, they divide students’ math knowledge into content and processes: “Content includes number and operations, algebra, geometry, measurement, and data analysis and probability. Processes include problem solving, reasoning and proof, communication, connections, and representations” (Metzger et al, 2019, p. 432; NCTM, 2000). By presenting a way to dissect student definitions, these authors offer a way to evaluate and compare student responses.

This organization of math ideas into either content or process is central to Metzger’s exploration of student knowledge of math across grade levels and how students conceptualize its usefulness (Metzger et al., 2019). As part of their method, students were interviewed and asked several questions about math. One key question was: “What is math?” (Metzger et al, 2019).

Based on their coding of student responses, a vast majority (91.9%) of students from grades one through four talked about math through its content. In contrast, only 12.1% of responses involved math processes, demonstrating a limited scope in thinking about math. Even when looking at those 91.9% of responses that talked about math content, most of those responses primarily focused on Numbers & Operations (89.9% of all responses). Other areas of math content including Algebra, Geometry, and Measurement were all mentioned by fewer than 10% of students (Algebra was discussed by 3.0% of students, Geometry was discussed by 8.1% of students, and Measurement was discussed by 7.1% of students) (Metzger et al., 2019). These results indicate that students have very limited definitions of math when compared to standards of math instruction as defined by the NCTM. Metzger suggests that this may be because students’ engagement with mathematics beyond the classroom is not explicitly connected to math, indicating a potential connection between students’ ideas of definitions and utility (Metzger et al., 2019).

Expectancy-Value Theory and Utility Value

Theories of learning and motivation in educational psychology are useful for teachers to increase students’ academic performance and engagement. Modern Expectancy-Value Theory (EVT) is a comprehensive and research-based model to consider the relationship between multiple variables related to student motivation. Some of those variables include students’ perceptions of their own competencies, perceptions of the difficulty of various tasks, and personal goals. Through considering these complex variables together, Eccles and Wigfield (2002) provide a guide for educators and researchers in understanding students’ motivations and how to tap into their potential.

Eccles and Wigfield dive into student expectations of success, as well as their beliefs about their own abilities, which are tied to their motivation to participate in class. When students believe they can be successful and that they are capable, it is easier to justify expended effort in learning. However, if they conclude that they will not be successful or are not capable, students are less likely to engage (Eccles & Wigfield, 2002). However, it is not enough for students to believe they will be successful; they must also have a purpose to attempt achievement. Thus, the theory also includes task-values, which are broken into four components: attainment value, intrinsic value, utility value, and cost (Eccles & Wigfield, 2002). Attainment value is related to personal importance and identity-building. This may include a sense of pride by being successful at a given task or acquiring prestige. Intrinsic value is the enjoyment brought on by completing the task itself and the inherent value of the task. Utility value is the perception of how useful engaging in a given task will be for future goals such as career planning. Finally, cost considers the associated negative aspects of a task, such as loss of time or energy, or potential trade-offs. Utility value is a worthwhile component to investigate further because of its malleability.

Within science and mathematics instruction, a number of studies show that utility-value interventions have positive effects on students’ academic outcomes. Hulleman and Harackiewicz (2009) demonstrated that when students are tasked with creating personal connections with the learning in their science courses, their interest and grades increased, and the effect size was greater for those who had low expectations of success. Canning and Harackiewicz (2015) reinforced those findings through their study on mathematics education, and they also emphasized that students are active in making these connections to their personal lives rather than just accepting the connections that their instructors have offered. Brown et al. (2015) explored how interventions focused on expanded notions of utility, such as including communal utility with existing ideas of self-oriented utility, led to both short-term and long-term increases in learning motivation in biomedical sciences. While these utility-value interventions demonstrated increased academic performance and motivation, another study found that a high perception of utility value in science and mathematics was a significant factor contributing to students’ self-selection of those courses in the earlier stages of students’ education (Caspi et al., 2019). Thus, a student’s perception of math’s utility value greatly influences their access to and selection for future math learning.

Student-Generated Utility

Utility value interventions that directly communicate the usefulness of math are not effective in improving academic performance for all students (Canning & Harackiewicz, 2015). In Canning and Harackiewicz’s studies, they compared the effect of directly communicated utility math interventions and self-generated utility math interventions on students. Forms of directly communicated utility value come from sources like parents or teachers. In their design, participants were randomly assigned to one of two utility value interventions. They first had students participate in a self-generated utility value intervention where they generated examples of math’s utility related to their own lives. The second had students participate in a directly communicated utility value intervention where students listened to an instructional presentation (Canning & Harackiewicz, 2015). Their findings reveal that directly communicated ideas of usefulness promoted performance for students with higher confidence in their math abilities, but they were detrimental to the performance of students who lacked confidence in math. In contrast, self-generated ideas of usefulness promoted math performance for all students, and this intervention was even more impactful for students with lower levels of confidence in their math abilities (Canning & Harackiewicz, 2015).

Student-generated ideas of utility allow students to imagine themselves as the users of math concepts. This research does not suggest that all directly communicated ideas of math utility value should be removed from the classroom. In the related studies, students’ perceived utility value of math increased in settings where direct communication and student-generated ideas of utility value happened concurrently (Canning & Harackiewicz, 2015). They suggest this may be because when done together, students have the opportunity to put directly communicated ideas about usefulness in their own words. Thus, direct communication of utility value in instruction is still valuable. But Dobie (2019a) points out the potential harm of emphasizing the usefulness of content when students do not feel that they are capable of using it. Remembering EVT, students will not feel motivated to engage in a task if they do not feel they can expect success or if they perceive that they are not capable.

Incorporating student-generated ideas of math expands notions of what could be useful beyond what instructors are currently offering through direct communication and direct teaching. Dobie (2019a) asserts that math instruction should be designed for student populations beyond the dominant cultural group by discussing a previously ignored way to think about utility. She highlights the need to attend to models of the self (Grossmann & Varnum 2011; Stephens et al. 2007) and discusses the differences between independent and interdependent conceptions of usefulness. Independent conceptions of usefulness focus on individual performance while interdependent conceptions of usefulness consider connectedness amongst individuals. Math instruction often focuses solely on independent conceptions of usefulness, but Dobie (2019a) suggests that some populations may benefit from expanded notions of utility that consider both perspectives. Other literature discusses similar ideas through agentic utility value which focuses on self-oriented usefulness and communal utility value which focuses on usefulness to help others (Brown et al., 2015). The effects of expanded notions of utility that include both self- oriented and communal utility values benefit all students in the classroom (Brown et al., 2015). Through acknowledging groups not previously considered, novel ideas emerge with serious potential to elevate student learning motivation. These expanded notions of utility are essential to consider when analyzing student-generated ideas about utility in math.

Approach to the Research

The current study focuses on understanding student-generated math definitions and notions of math utility concurrently. This is because there may be a correlative relationship between students’ definitions and their sense of its utility. Metzger and her colleagues (2019) show that students had a narrow scope of mathematics within their study on student conceptions of math utility. This research aligns with Johansson and Sumpter’s (2010) study about how students think of math as something that occurs at a desk in class. This reinforces Metzger’s (2019) findings where students shared math ideas demonstrating math as content where something is learned in school, and not a process or something they engage with or do as an action. To improve student motivation through utility value, existing research demonstrates that students must envision themselves as actors and users of math through generating their own ideas of its usefulness (Canning & Harackiewicz, 2015). Expanding their definitions of math to include processes and expanding their notions of its utility are thus related and should be studied concurrently.

The current study focuses on middle school students and their ideas about math because this age group is specifically important to consider as they are in a critical period regarding their relationship with math learning. During these years, in which there is greater emphasis on math and science learning, students display significant declines in learning motivation and begin to develop deeper personal identities as individuals and as learners (Dweck & Master, 2009; Eccles, 2009). Priniski and Thoman (2020) highlight that in the broader school structure of the United States, middle school years are also the first time that students have autonomy in course selection and are more subject to being put on different course tracks. Thus, this time is indispensable in setting up the future of their opportunities for math education. With all these factors together, middle school students are an excellent group of sample participants for on-going research.

Methods

Data were collected through interviews with 8th-grade students attending an urban charter school in the Mountain West. These interviews were conducted between April and May of 2022. Interviews ranged from 26 to 45 minutes (mean = 35.7 minutes) and included questions focusing on students’ ideas about mathematics and its usefulness. Student definitions of math were coded using the content and process standards from the National Council of Teachers of Mathematics similar to the coding in Metzger’s study (Metzger et al., 2019; NCTM, 2023). Student conceptions of utility were coded using categories from Dobie’s previous research (2019b) on student perspectives of math utility. The relationship between definition and utility was further explored by looking at the most common utility connections made with each math definition category.

Participants

Participants were identified for this study through a cooperating teacher. Students who volunteered to participate received a $10 gift card incentive. Each of the 10 participants were in 8th-grade and aged between 13 and 14 years old (mean age = 13.4 years). Six students described their gender as male, 3 as gender non-conforming, and 1 as female. Students were asked to describe their race or ethnicity using as many identifications as they felt appropriate. Of the 10 participants, 40% identified as white, 40% identified as Hispanic or Latino, and 20% reported as both African American and Hispanic or Latino. In a post-interview survey, students were asked to answer a few questions about their own competencies in math on a scale from 1 to 7. The first of these questions asked: “How good at math do you think you are?” with 1 being “Not good at all” and 7 being “Very good.” The mean response from participants was 4.8 (ranging from 3 to 6). Second, the students were asked: “If you were to rank all the students in your math class from the worst to the best in math, where would you put yourself?” with 1 being “The worst” and 7 being “The best.” The mean response from participants was 4.5 (ranging from 3 to 6). Third, the students were asked: “How well do you think you will do in math this year?” with 1 being “Not well at all” and 7 being “Very well.” The mean response from participants was 4.5 (ranging from 4 to 6).

Interviews

Interviews were semi-structured and largely guided by predetermined questions, but follow-up questions were integral to the interview process. For the present study, select questions were chosen from the interviews to focus on the research questions.

Key questions used to analyze responses for student-generated definitions came from the early portions of the interview, and students were asked: “Imagine that a new kid moved to your neighborhood and that kid has never taken a math class before or even heard the word ‘math’. Can you pretend I’m that new kid and tell me, what is math?” Some follow-up questions asked for more explanation or clarification. To expand their thinking on this question, students were also asked: “When I say the word ‘math’, what words or pictures come to mind?” The key question used to analyze and code responses related to math definitions differs from prior research. In Metzger’s study, they asked: “What is math?” (Metzger et al., 2019). This difference in framing of the question was part of the design because of the difficulties students experienced in defining mathematics in prior research (McDonough & Sullivan, 2014). Thus, the question’s framing is intended to offer context for students. It is intended to create better access to understanding what the question is asking and to create a launching point for students to craft their answers.

Key questions used to analyze responses for student-generated notions of math utility were pulled from the beginning of the interview and from the later portions of the interview. One key question about utility from the beginning of the interview asked: “When I was a teacher, some of my students would say math is useful, and some of them would ask when we’re ever going to use math and say it’s not useful. What do you think? Who do you agree with?” Some common follow-up questions include: “Why do you think math is useful/not useful?”, “Why do you think some of my students said math isn’t useful?”, and “If someone disagrees with you, how could you try to prove to them that math is (or isn’t) useful?” The interviewers offered their own experiences through this question to encourage students to be more honest in their own responses when thinking about whether math is useful, so they do not say only what they think the interviewer wanted to hear. Additionally, this framing of the question asked students to explain why math is useful rather than just offer examples. While their answers may have included examples, it was focused on answering why math is useful rather than just how it is useful. This allowed more alignment with the coding scheme for math utility whereas examples of math being useful may have led them to continue answering how they would define math and what they think math includes.

Additional questions were selected for analysis from the end of the interview. The first of these questions asked students, “Can you think of any people in your life who use math regularly?” This question is aimed to have students think about where they see math used and to frame it through their own experiences rather than just offer directly communicated forms of utility they may have received from teachers or others. This question required the notion of utility to come from the students’ own observations. Similarly, the students were asked, “Do you use math regularly in your life?” to learn more about their personal experiences and conceptions of math. Follow-up questions were asked about when they use math, how they use math, and what kinds of math they use.

Next, students were asked, “Do you have a job or career in mind that you want to pursue in the future?” and if students responded with an example job or career, they were asked, “Do you think you will need to know math to get that job or to do that kind of work?” They were asked about how these related to math, and these questions allowed students to offer notions of utility that connected to their futures and not just their current experiences and daily routines. This connection to their future is essential to fully analyzing their sense of math’s utility as it is a key component of utility value in EVT (Eccles & Wigfield, 2002).

Finally, students were asked, “Do you have any other kinds of goals for your future, or things that are really important to you in your life?” and if they responded with examples, then they were asked: “Do you imagine math being helpful with those in any way? Why or why not?” It was important to not just ask about one potential area where they may use math in the future. For example, it would have limited the analysis if students were only asked about math in relation to their future career as this does not reflect diverse notions of utility (Dobie,

2019b). The end of the interview was left open for students to share any additional thoughts or to ask questions; however, these did not contribute to the data analysis regarding student definitions and notions of utility.

Data Analysis

After the data was collected from the interviews, responses to the key questions were sorted into a coding scheme that included definition and utility sections. One key question with follow-up answers was used to code for student-generated definitions. Each student response to this question was analyzed for evidence of student ideas related to the NCTM standards. These standards were split into Content and Process. Content standards include Number & Operations, Algebra, Geometry, Measurement, and Data Analysis & Probability (NCTM, 2023). Process standards include Problem Solving, Reasoning & Proof, Communication, Connections, and Representations (NCTM, 2023). The descriptions of these standards from NCTM were used in sorting responses. Responses were then assigned a raw score out of the 10 total standards that represented the scope of the student definition. This raw scope only measured the breadth of student responses and did not represent the quality of their connections to these different standards.

Five key questions were used in the coding scheme to analyze students’ notions of math’s utility. Answers from these five questions were then coded, and responses were analyzed for evidence related to four utility domains using Dobie’s previous research on utility value related to math education (2019b). The first utility domain was titled Everyday Life (General) in the coding scheme. This domain focused on broader claims about math being useful such as “Math is everywhere!” or “Math can be used in anything!” The second utility domain was titled Future Job/Career. The third utility domain was titled Daily Activities, and this domain was focused on specific examples of how math is useful in day-to-day life. Common examples were cooking, budgeting, and time management. The fourth utility domain was titled Current or Future Schooling. Some student connections to these utility domains were explicit, but other coding decisions were made by the judgment of the coder. Similar to the coding of responses to the definition question, responses were assigned a raw score out of 4 to represent the 4 utility domains, and this score only demonstrated the breadth of their sense of math’s utility, not the thoroughness or quality of student responses.

After responses were coded, the data was analyzed to look for connections between students’ math ideas of definitions and utility. Initially, connections were analyzed to see which areas of math defined by the NCTM standards were most frequently paired with which utility domains. Then, each students’ breadth of math definition ideas and math utility ideas were compared to see if a wider breadth of math definition was related to a wider breadth of thinking about math’s utility.

Findings

Using the selected questions from the interview and the coding scheme, students’ responses were analyzed. First, the definition question was used to connect student ideas with the NCTM standards. Second, the utility questions were used to connect student ideas with the utility domains. Then, the data was analyzed together to look for connections in students’ ideas about defining math and using math.

Student-Generated Definitions and Notions of Utility

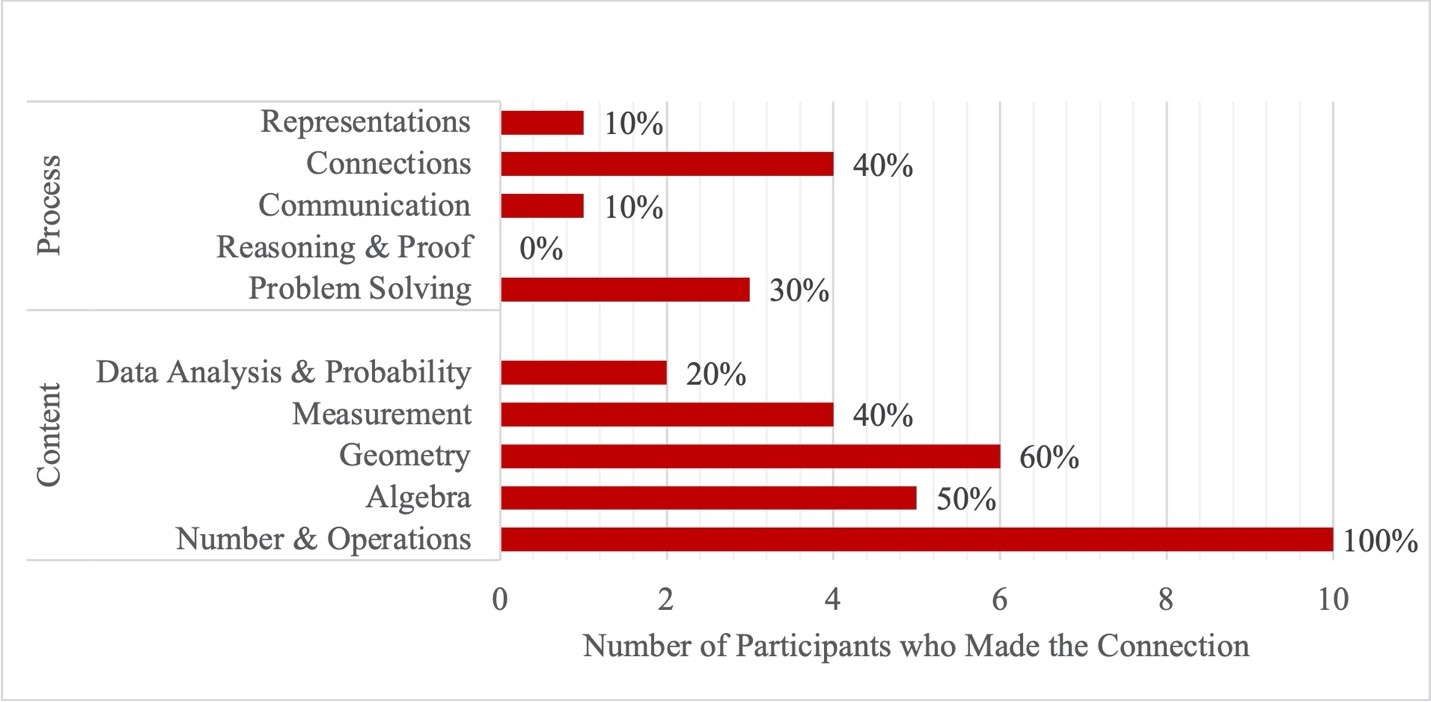
Responses were analyzed for evidence of connections to the different NCTM standards. The standard with the most frequent student-made connections was Number & Operations, which was mentioned by 100% of participants. Students frequently began their definitions by listing operations such as multiplication or division. Many others mentioned numbers and fractions. One student’s initial response was: “I think I would say math is pretty much these numbers that you can add, subtract, multiply, or divide with and they come up with a number that you can like do some more with the number you got.” The standard with the least frequent student-made connections was Reasoning & Proof, which was not mentioned in any of the interviews. Overall, content standards emerged with much greater frequency than process standards, as seen in Figure 1. It seems that the majority of students in the sample were more likely to imagine math as a topic and as content while fewer students imagined math as something that is practiced through processes.

Figure 1: Frequency of Mathematical Ideas Emerging in Student Definitions

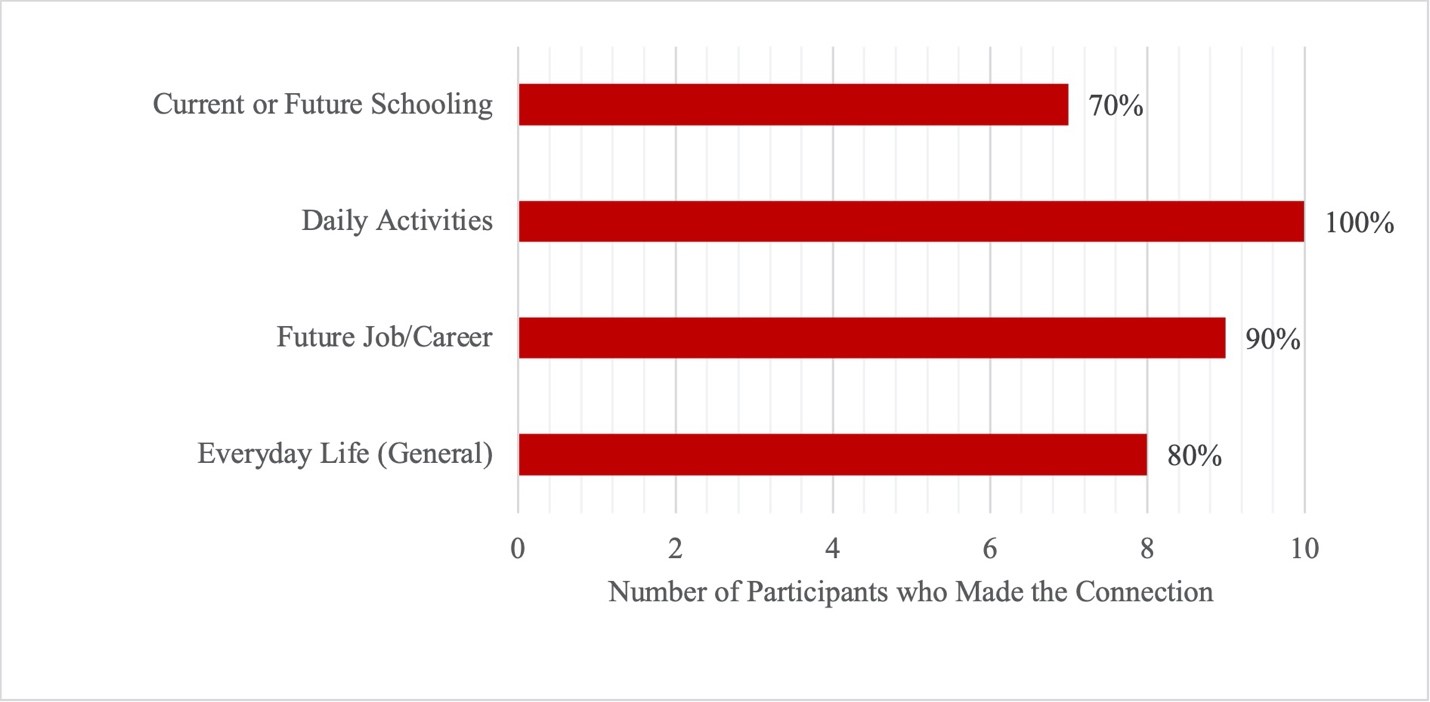
Additionally, all participating students were able to generate some ideas of math’s utility, as represented in Figure 2. The domain with the most frequent student-made connections was Daily Activities, which was mentioned in 100% of the interviews. Responses frequently involved money, measurements for various purposes, and time management. Related to time management, one student shared: “…when I’m trying to figure out like, uh, time management, which I struggle with a lot, so when I’m trying to plan my day, I have to do math on like, okay, estimating how much time I’m going to walk my dog, how much time I’m going to work on my homework, that kind of stuff.” Some began detailing rich examples of math’s usefulness in daily activities by talking about instances of specific problem solving such as with vaccines: “I believe that it is useful, and um, that you are going to need it in some scenarios because it’s such a relevant thing in our society. Um, especially if you’re working in jobs like engineers. And, um, people who need to know math to make our world work … people who make the vaccines, and, um, health administration. And just in general, people who, everyday people who, who come across a problem they need to solve, most of them are math-related.” Connections to the utility domain Future Job/Careers were made in 90% of responses. The most frequently mentioned jobs and careers were cashiers, engineers, and teachers. Connections to the utility domain Everyday Life (General) were made in 80% of responses. These responses usually communicated that math is simply needed to do many things like survive. One student shared: “… if they think it’s not useful, like how they’re gonna survive without like knowing how to multiply or like adding or something for like the real world because they’re gonna need it either way.” Connections to the utility domain Current or Future Schooling were mentioned in 70% of responses. These responses typically discussed using math in school, doing homework, or seeing other students use math for school. Many students articulated that math can be useful without any awareness that it is being used. Thus, students’ sense of usefulness is not limited to their definitions of math.

Figure 2: Frequency of Utility Domains Across Student Responses

Definition and Utility Connections

After analyzing student-generated definitions and notions of utility, the ideas were looked at concurrently. This was done in two ways. First, the NCTM standards that were mentioned by each student in response to the definition question were compared with their answers to utility questions. Some ideas related to NCTM standards were mentioned with no utility connection, but this analysis was specifically looking at the frequency of a definition area being connected to a utility domain. This analysis explores how students think of different areas of math as useful in specific ways. Second, the overall breadth in emerging ideas from students related to their definitions of math and notions of utility were compared. Their individual responses were scored comparing the breadth of NCTM standard connections and utility domains mentioned in their interview. This analysis helps us to see whether having a broader definition of math is connected with a broader sense of its utility.

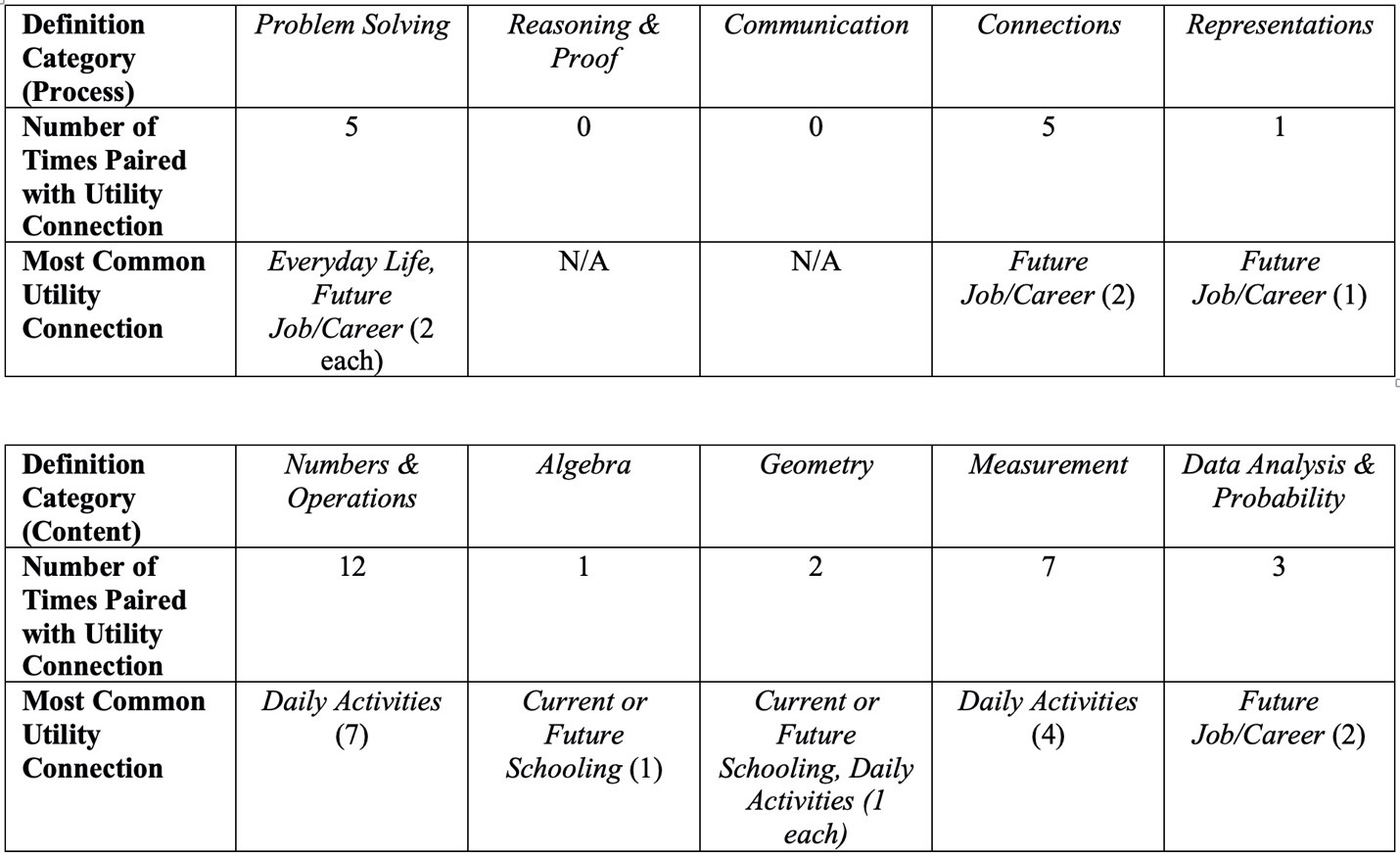
The frequency of definition areas being connected to utility domains represents how different NCTM standards are perceived as useful and in what ways a certain area of math is considered useful by students. These findings can be seen in Table 1. Among the content standards, Number & Operations had the most connections to utility domains with 12 total mentions. Of those 12 connections to utility areas, seven were to Daily Activities. Not all students mentioned examples of Number & Operations in their interviews, but other students connected this standard to multiple utility domains. A handful of students specifically connected Number & Operations to both Future Job/Career and Daily Activities. This meant that the overall utility connections made for this standard exceeded the total number of participants. Number & Operations having the most utility connections makes sense as it was also the most frequently mentioned NCTM standard from the definition questions. However, the definition area with the second most utility connections was only mentioned by 40% of participants, and this definition area was the NCTM standard, Measurement. Responses contained seven connections between Measurement and utility domains with four of those connections being related to Daily Activities. Some definition areas and NCTM standards had no utility domain connections, such as Communication and Connections.

Table 1: NCTM Definition Areas and Most Frequent Utility Domain Connections

After looking at the kinds of connections made between definition areas and utility domains, the overall breadth of definitions and notions of utility were compared for each student. Each student response was given a score for their scope of definition and a score for their scope of utility. Their responses to the definition question were scored out of 10 with a percentage.

This score reflected how many of the 10 NCTM standards emerged in their response. Students’ scopes and breadth in response to the definition question ranged from 10% to 60% with a mean of 37%. Furthermore, their responses to the utility questions were scored together out of 4 with a percentage. This score represented how many connections were made to the 4 utility domains.

Students’ scopes and breadth in response to the utility questions ranged from 75% to 100% with a mean of 87.5%. There were no overarching patterns in students’ scope of mathematics in relation to their scope of utility notions as seen in Table 2. What was interesting from this analysis was the comparison between students with the greatest and smallest scope in definition. Both the student with the widest definition scope score (60%) and the student with the narrowest definition scope score (10%) had a 75% scope score in response to the utility questions. Thus, students’ ability to explain examples of math utility was not related to their scope in definition.

Table 2: Individual Students’ Definition Breadth Score and Utility Notion Breadth Score

Discussion

These findings connect to prior research in important ways. However, we must also consider the limitations of this work. Finally, we can consider the implications of the present study for future research and for future practice.

Relation to Metzger’s Work

The present study’s methods of analyzing student-generated definitions of mathematics were influenced by Metzger’s work (2019) to understand students’ conceptions of mathematics. However, there are some important differences between these studies. First, the framing of the questions asked in the interviews to collect data on student ideas was different. In Metzger’s interviews, they asked students: “What is math?” whereas in the current study, students were asked: “Imagine that a new kid moved to your neighborhood and that kid has never taken a math class before or even heard the word ‘math’. Can you pretend I’m that new kid and tell me, what is math?” Additionally, the age of participants across these studies differed. Metzger’s work focused on elementary aged students entering grades one through four (2019). In the current study, middle students were the focus with participants all being in eighth grade. The sample size of these studies also differed. In the 2019 study, there were 99 participants compared to the 10 participants in the current study, and the 2019 sample had greater racial and ethnic diversity than the current study (Metzger et al., 2019). While there are some differences between the studies, important insights can still be made by comparing the two.

Results from Metzger’s study showed a large majority of students focused their ideas about math on content areas of math (91.9% of responses) over processes with the majority of those responses focused on Number & Operations (89.9% of responses) (Metzger et al., 2019). These findings align with the current study where 100% of participants mentioned ideas related to Number & Operations. However, the present study had more diverse ideas emerge related to the NCTM standards than Metzger’s work. Focusing on just content standards, Algebra was discussed by 3% of students in Metzger’s study compared to 50% in the present study. Geometry was discussed by 8.1% of students in Metzger’s study compared to 60% in the present study. Measurement was discussed by 7.1% of students in Metzger’s study compared to 40% of students in the present study. Metzger’s work did not report data on how many students mentioned Data Analysis & Probability, but the present study had 20% of students mention ideas related to this standard. When looking at process standards, the present study also shows a greater percentage of students mentioning ideas related to NCTM process standards. In Metzger’s work, they only reported data for Problem Solving and Connections. In their study, 5.1% of students mentioned ideas related to Problem Solving compared to 30% in the present study. Connections were discussed by 5.1% of students in Metzger’s study compared to 40% of students in the present study. We can see two potential reasons for a greater scope in defining mathematics amongst the participants in the present study. First, this difference may be because students in the present study are older and have had more math education. Thus, students’ conceptions of mathematics may continue to expand as they enter junior high, and these conceptions are not fixed. Second, this difference may be a result of the difference in framing the question. There is potential that the framing of the question in the present study with follow-up questions encouraged students to think about the prompt more deeply and to extend the scope of their thinking.

Limitations and Future Directions for Research

While there are practical applications for teachers and future research from this study, there are also limitations to consider. First, there are some limitations from the study’s sample. The sample size was very limited with only 10 participants. This makes it difficult to generalize the results to other contexts. Additionally, there is a lack of gender diversity in the demographics of participants.

Second, there were some limitations related to the interview process. The framing of the definition question was intentional to offer students more context and access to sharing their ideas about math. However, some of the interviews revealed potential issues with this framing. The question asks students to explain what math is to someone who had never heard of math or taken a math class. In response, one student had started to include concepts like numbers, adding, symbols, equations, and more. They were explaining these concepts in a sequence in which they thought math should be taught. They began to explain the reasoning behind this thinking: “I probably wouldn’t want to instantly start teaching the dude [the imagined new student] square roots and cubic roots and division.” This response spurs questions about other students who potentially interpreted the question as a way to teach math rather than define math. Perhaps the framing of the question removed students’ intention to define mathematics and limited their answers to their perceptions of the more accessible parts of math. Within this study, this limitation is partially remedied by the follow-up question where students were asked about other words and pictures that come to mind when thinking about math. However, this question does not directly prompt students with the intention to define math; it asks students to think about ideas related to math. Thus, future research that aims to understand how students define math should offer more access and launching points, but should also ask follow-up questions that allow students to attempt to define math. Future interviews may start with questions like this interview that offer launching points for students without influencing their responses with other stimuli and follow these questions with explicit questions about defining math.

Additionally, connections might have emerged in students’ responses on some questions other than those selected for the present study. This means that students’ scope of math’s usefulness may not be totally represented in this data analysis. On the opposite end, follow-up questions that connected to other portions of the interview may have caused students to give more detail that was then coded for the data analysis. These follow-up questions might not have been offered equitably across participants. This limitation is because the data analysis was organized after the interviews were conducted. Future research that asks about the relationship between student-generated ideas, whether that be definitions and utility or other concepts, should ask these questions in a sequential order at the start of the interview without other questions in between that may influence student responses.

Third, there are some potential issues related to data analysis. One of these issues was that there was only one coder. Thus, there is no inter-rater reliability for these findings. Another issue with data analysis concerns a question selected for coding responses. This question asked about students’ future career aspirations with follow-up questions about how math may be related to those careers. This greatly increased the probability that students would offer ideas in their interview that demonstrated connection to the utility domain, Future Job/Career. While this question and other questions did not guarantee that students would make mentions of ideas related to Future Job/Career, there is a strong likelihood that student responses were influenced by the direct questioning related to this utility domain. Thus, future analyses should explore how frequently job and career connections emerged solely on questions where students were not explicitly asked about their future career interests.

The last potential issue related to data analysis was the way the breadth of students’ definitions was evaluated. The way students’ answers were compared to NCTM standards only accounted for whether a connection was made based on the coder’s interpretation. If a student made several connections to one NCTM standard, this still only expanded their breadth score by 10% and would reflect the same breadth in definition as a student who only offered one example. Additionally, this method did not allow any analysis of the quality of students’ connections to reflect how deeply they understand how math is used in various ways. Future research should consider ways to evaluate multiple aspects of a student’s definition about math including the breadth of math topics, the quantity of examples, and the quality of their thinking.

Implications for Future Research

The present study cannot make a definitive conclusion about the nature of students’ conceptions about mathematics and whether they are fixed or dynamic. However, the comparison between Metzger’s study and the current study suggests students are able to expand their definitions to include a broader scope of ideas in both content areas and processes of math (Metzger et al., 2019). Thus, future research should continue to inquire about student-generated definitions of math to examine how those definitions change over time, what factors change those definitions, and at what point in students’ educational career their ideas are most fluid and adaptive.

Furthermore, the definition-focused questions about math in the interviews in the present study diverged from previous research. Where existing studies have asked more direct questions such as, “What is math?” or “What is maths all about?”, the current study offered more context to the question in efforts to offer a point of entry to the question to enrich students’ opportunities to offer rich answers (McDonough & Sullivan, 2014; Metzger et al., 2019). This difference in setting up the interview question may have strengths and weaknesses. Thus, future research should focus on the most effective ways to collect students’ conceptions about math and what they include in their personal definitions.

Implications for Practice

Teachers should informally collect information about their students’ math definitions and notions of math utility. Teachers do not need to sit down and record student answers, but as they get to know their students, they can use these findings to guide in-class discussions related to math. As they move between math concepts and topics in their curriculum, they should invite students to share where they imagine they can use what they learn. This information sharing will both lead to more meaningful learning for students as they practice generating their own notions of math utility (Hulleman & Harackiewicz, 2009) and will also inform teachers about the specific utility values of the unique students in their classroom. This will allow the teacher to make instructional decisions that are most relevant to their classrooms and most individualized to their students. This is a particularly valuable change to instruction for teachers to make as it may include expanded notions of utility that have previously not been the focus of utility interventions in math (Dobie, 2019b).

Teachers should consider how much emphasis they place on various math standards in their classrooms that may be leading to such a preference for students to discuss topics like Number & Operations over Reasoning & Proof or Representations. Additionally, they should think about the framing of their math instruction that leads students to think of math as a topic that is studied through content areas rather than by participating in processes, and this commonality in student thinking is supported both by the present study and by previous findings (Metzger et al., 2019). Teachers should rethink the opportunities they facilitate in their classrooms to allow students to use math in practice instead of what previous research has shown where students think about math as something done alone, at a desk, and in a math book (Johnasson & Sumpter, 2020). Metzger et al. (2019) suggest that there is a lack of meaningful math connections explicitly made for students; however, other researchers argue that students benefit more from opportunities to create their own notions of utility (Hulleman & Harackiewicz, 2009). The present study showed that students are able to generate a broad range of examples where math is useful. To build students’ conceptions about math including both their definitions and sense of usefulness, instead of making explicit math connections to real-world contexts, teachers should create opportunities for students to generate their own sense of utility related to each math topic and process they use in their classroom throughout the year. Elementary and middle-school students might need more support in thinking about possibilities since their world experiences are more limited than the participants in some of the previous studies. These opportunities may benefit students’ learning in broadening their conceptions of math while simultaneously building their motivation through math’s utility value (Eccles & Wigfield, 2002). Teachers should use their own expertise about their classrooms and the age groups they work with to determine what this looks like, whether it be math journaling, writing story problems, more in-class discussions, or other.

Conclusion

This research echoes previous literature and urges teachers and researchers to consider student-generated ideas. Returning to the research questions, middle school students define math primarily through its content over its processes. Math content was most frequently seen as useful through Daily Activities, while math processes were most frequently seen as useful in Future Job/Careers. However, there was no evidence of a correlative relationship between students’ math definitions and their notions of math’s utility. Thus, teachers should take every opportunity to expand their students’ definitions of math while simultaneously providing opportunities for students to make personally meaningful connections with their math learning.

References

Brown, E. R., Smith, J. L., Thoman, D. B., Allen, J. M., & Muragishi, G. (2015). From bench to bedside: A communal utility value intervention to enhance students’ biomedical science motivation. Journal of Educational Psychology, 107(4), 1116-1135. Retrieved from http://dx.doi.org/10.1037/edu0000033

Canning, E. A., & Harackiewicz, J. M. (2015). Teach it, don’t preach it: The differential effects of directly-communicated and self-generated utility–value information. Motivation Science, 1(1), 47–71. Retrieved from https://doi.org/10.1037/mot0000015

Caspi, A., Gorksy, P., Nitzani-Hendel, R., Zacharia, Z., Rosenfeld, S., Berman, S., & Shildhouse,

B. (2019). Ninth-grade students’ perceptions of the factors that led them to major in high school science, technology, engineering, and mathematics disciplines. Science Education, 103(5), 1176-1205. Retrieved from https://doi.org/10.1002/sce.21524

Eccles, J. (2009). Who am I and what am I going to do with my life? Personal and collective identities as motivators of action. Educational Psychologist, 44(2), 78–89. Retrieved from https://doi.org/10.1080/00461520902832368

Eccles, J. S., & Wigfield, A. (2002). Motivational Beliefs, Values, and Goals. Annual Review of Psychology, 53(1), 109-132. Retrieved from http://doi.org/10.1146/annurev.psych.53.100901.135153

Dobie, T. (2019a). A sociocultural examination of utility value in mathematics: The role of interdependence in middle school students’ perceptions of usefulness. In M. Hannula, G. Leder, F. Morselli, M. Vollstedt & Q. Zhang (Eds.), Affect and Mathematics Education, 67-88. Springer. Retrieved from https://link.springer.com/chapter/10.1007/978-3-030-13761-8_4

Dobie, T. (2019b). Expanding conceptions of utility: middle school students’ perspectives on the usefulness of mathematics. Mathematical Thinking and Learning, 21(1), 28-53. Retrieved from https://doi.org/10.1080/10986065.2019.1564969

Dweck, C. S., & Master, A. (2009). Self-theories and motivation: Students’ beliefs about intelligence. In K. R. Wenzel & A. Wigfield (Eds.), Handbook of motivation at school, 123–140. Routledge/Taylor & Francis Group. Retrieved from https://psycnet.apa.org/record/2009-24219-007

Grossmann, I., & Varnum, M. E. W. (2011). Social Class, Culture, and Cognition. Social Psychological and Personality Science, 2(1), 81–89. Retrieved from https://doi.org/10.1177/1948550610377119

Hulleman, C. S., & Harackiewicz J. M. (2009). Promoting interest and performance in high school science classes. Science, 326(5958). Retrieved from https://www.science.org/doi/10.1126/science.1177067

Johansson, A. D., & Sumpter, L. (2020). Children’s conceptions about mathematics and mathematics education. Current State of Research on Mathematical Beliefs XVI. Retrieved from https://www.researchgate.net/publication/339413153_CHILDREN%27S_CONCEPTIONS_ABOUT_MATHEMATICS_AND_MATHEMATICS_EDUCATION

Moll, L. C., Amanti, C., Neff, D., & Gonzalez, N. (1992). Funds of knowledge for teaching: using a qualitative approach to connect homes and classrooms. Theory Into Practice, 31(2), 132–141. Retrieved from http://www.jstor.org/stable/1476399

McDonough, A., & Sullivan, P. (2014). Seeking insights into young children’s beliefs about mathematics and learning. Educational Studies in Mathematics, 87(3), 279–296. Retrieved from https://doi.org/10.1007/s10649-014-9565-z

Metzger, S. R.; Sonnenschien, S.; & Galindo C. (2019). Elementary-age children’s conceptions about mathematics utility and their home-based mathematics engagement. The Journal of Educational Research, 112(4), 431-446. Retrieved from https://doi.org/10.1080/00220671.2018.1547961

National Council of Teachers of Mathematics (NCTM). (2000). Principles, standards, and expectations. Reston, VA: NCTM. Retrieved from https://www.nctm.org/Standards-and- Positions/Principles-and-Standards/Principles,-Standards,-and-Expectations/

Stephens, N. M.; Markus, H. R.; & Townsend, S. S. M. (2007). Choice as an act of meaning: The case of social class. Journal of Personality and Social Psychology, 93(5), 814–830. Retrieved from https://doi.org/10.1037/0022-3514.93.5.814

Priniski, S. J., & Thoman, D. B. (2020). Fostering an Inclusively Relevant Mathematics Environment: The Case for Combining Social-Justice and Utility-Value Approaches. Retrieved from https://doi.org/10.31219/osf.io/wsx9d