4 Measurements
OpenStax
LEARNING OBJECTIVES
- Explain the process of measurement.
- Identify the three basic parts of a quantity.
- Describe the properties and units of length, mass, volume, density, temperature, and time.
- Perform basic unit calculations and conversions in the metric and other unit systems.
Measurements provide much of the information that informs the hypotheses, theories, and laws describing the behavior of matter and energy in both the macroscopic and microscopic domains of chemistry. Every measurement provides three kinds of information: the size or magnitude of the measurement (a number), a standard of comparison for the measurement (a unit), and an indication of the uncertainty of the measurement. While the number and unit are explicitly represented when a quantity is written, the uncertainty is an aspect of the measurement result that is more implicitly represented and will be discussed later.
The number in the measurement can be represented in different ways, including decimal form and scientific notation. (Scientific notation is also known as exponential notation; a review of this topic can be found in Appendix B.) For example, the maximum takeoff weight of a Boeing 777-200ER airliner is 298,000 kilograms, which can also be written as [latex]\text{2.98 }\text{x 10}^5\text{ kg}[/latex]. The mass of the average mosquito is about 0.0000025 kilograms, which can be written as [latex]\text{2.5 }\text{x 10}^{-6}\text{ kg}[/latex].
Units, such as liters, pounds, and centimeters, are standards of comparison for measurements. A 2-liter bottle of a soft drink contains a volume of beverage that is twice that of the accepted volume of 1 liter. The meat used to prepare a 0.25-pound hamburger weighs one-fourth as much as the accepted weight of 1 pound. Without units, a number can be meaningless, confusing, or possibly life threatening. Suppose a doctor prescribes phenobarbital to control a patient’s seizures and states a dosage of “100” without specifying units. Not only will this be confusing to the medical professional giving the dose, but the consequences can be dire: 100 mg given three times per day can be effective as an anticonvulsant, but a single dose of 100 g is more than 10 times the lethal amount.
The measurement units for seven fundamental properties (“base units”) are listed in the table below. The standards for these units are fixed by international agreement, and they are called the International System of Units or SI Units (from the French, Le Système International d’Unités). SI units have been used by the United States National Institute of Standards and Technology (NIST) since 1964. Units for other properties may be derived from these seven base units.
| Base Units of the SI System | ||
|---|---|---|
| Property Measured | Name of Unit | Symbol of Unit |
| length | meter | m |
| mass | kilogram | kg |
| time | second | s |
| temperature | kelvin | K |
| electric current | ampere | A |
| amount of substance | mole | mol |
| luminous intensity | candela | cd |
Everyday measurement units are often defined as fractions or multiples of other units. Milk is commonly packaged in containers of 1 gallon (4 quarts), 1 quart (0.25 gallon), and one pint (0.5 quart). This same approach is used with SI units, but these fractions or multiples are always powers of 10. Fractional or multiple SI units are named using a prefix and the name of the base unit. For example, a length of 1,000 meters is also called a kilometer because the prefix kilo means “one thousand,” which in scientific notation is 103 (1 kilometer = 1,000 m = 103 m). The prefixes used and the powers to which 10 are raised are listed in the table below.
| Common Unit Prefixes | |||
|---|---|---|---|
| Prefix | Symbol | Factor | Example |
| femto | f | 10−15 | 1 femtosecond (fs) = 1 × 10−15 s (0.000000000000001 s) |
| pico | p | 10−12 | 1 picometer (pm) = 1 × 10−12 m (0.000000000001 m) |
| nano | n | 10−9 | 4 nanograms (ng) = 4 × 10−9 g (0.000000004 g) |
| micro | µ | 10−6 | 1 microliter (μL) = 1 × 10−6 L (0.000001 L) |
| milli | m | 10−3 | 2 millimoles (mmol) = 2 × 10−3 mol (0.002 mol) |
| centi | c | 10−2 | 7 centimeters (cm) = 7 × 10−2 m (0.07 m) |
| deci | d | 10−1 | 1 deciliter (dL) = 1 × 10−1 L (0.1 L) |
| kilo | k | 103 | 1 kilometer (km) = 1 × 103 m (1000 m) |
| mega | M | 106 | 3 megahertz (MHz) = 3 × 106 Hz (3,000,000 Hz) |
| giga | G | 109 | 8 gigayears (Gyr) = 8 × 109 yr (8,000,000,000 yr) |
| tera | T | 1012 | 5 terawatts (TW) = 5 × 1012 W (5,000,000,000,000 W) |
SI Base Units
The initial units of the metric system, which eventually evolved into the SI system, were established in France during the French Revolution. The original standards for the meter and the kilogram were adopted there in 1799 and eventually by other countries. This section introduces four of the SI base units commonly used in chemistry. Other SI units will be introduced in subsequent chapters.
Length
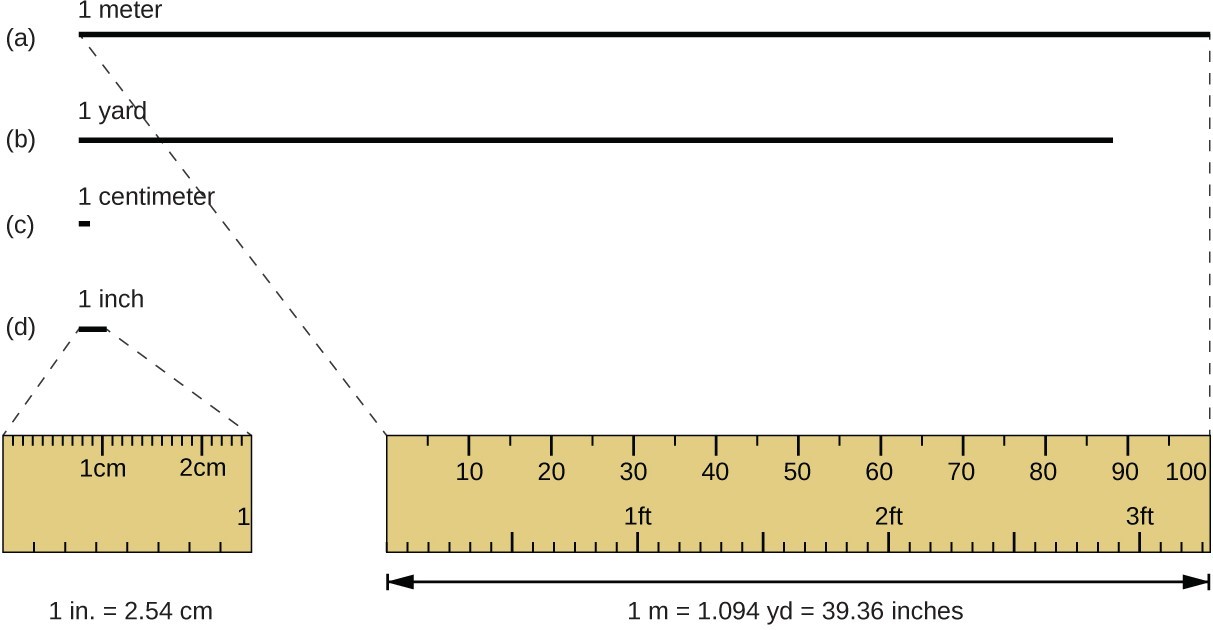
The standard unit of length in both the SI and original metric systems is the meter (m). A meter was originally specified as 1/10,000,000 of the distance from the North Pole to the equator. It is now defined as the distance light in a vacuum travels in 1/299,792,458 of a second. A meter is about 3 inches longer than a yard; one meter is about 39.37 inches or 1.094 yards. Longer distances are often reported in kilometers (1 km = 1000 m = 103 m), whereas shorter distances can be reported in centimeters (1 cm = 0.01 m = 10−2 m) or millimeters (1 mm = 0.001 m = 10−3 m).
Mass
The standard unit of mass in the SI system is the kilogram (kg). The kilogram was previously defined by the International Union of Pure and Applied Chemistry (IUPAC) as the mass of a specific reference object. This object was originally one liter of pure water, and more recently it was a metal cylinder made from a platinum-iridium alloy with a height and diameter of 39 mm. In May 2019, this definition was changed to one that is based instead on precisely measured values of several fundamental physical constants1. One kilogram is about 2.2 pounds. The gram (g) is exactly equal to 1/1000 of the mass of the kilogram (10−3 kg).

Temperature
Temperature is an intensive property. The SI unit of temperature is the kelvin (K). The IUPAC convention is to use kelvin (all lowercase) for the word, K (uppercase) for the unit symbol, and neither the word “degree” nor the degree symbol (°). The degree Celsius (°C) is also allowed in the SI system, with both the word “degree” and the degree symbol used for Celsius measurements. Celsius degrees are the same magnitude as those of kelvin, but the two scales place their zeros in different places. Water freezes at 273.15 K (0 °C) and boils at 373.15 K (100 °C) by definition, and normal human body temperature is approximately 310 K (37 °C). The conversion between these two units and the Fahrenheit scale will be discussed later in this chapter.
Time
The SI base unit of time is the second (s). Small and large time intervals can be expressed with the appropriate prefixes; for example, 3 microseconds = 0.000003 s = 3 × 10−6 and 5 megaseconds = 5,000,000 s = 5 × 106 s. Alternatively, hours, days, and years can be used.
Derived SI Units
We can derive many units from the seven SI base units. For example, we can use the base unit of length to define a unit of volume, and the base units of mass and length to define a unit of density.
Volume
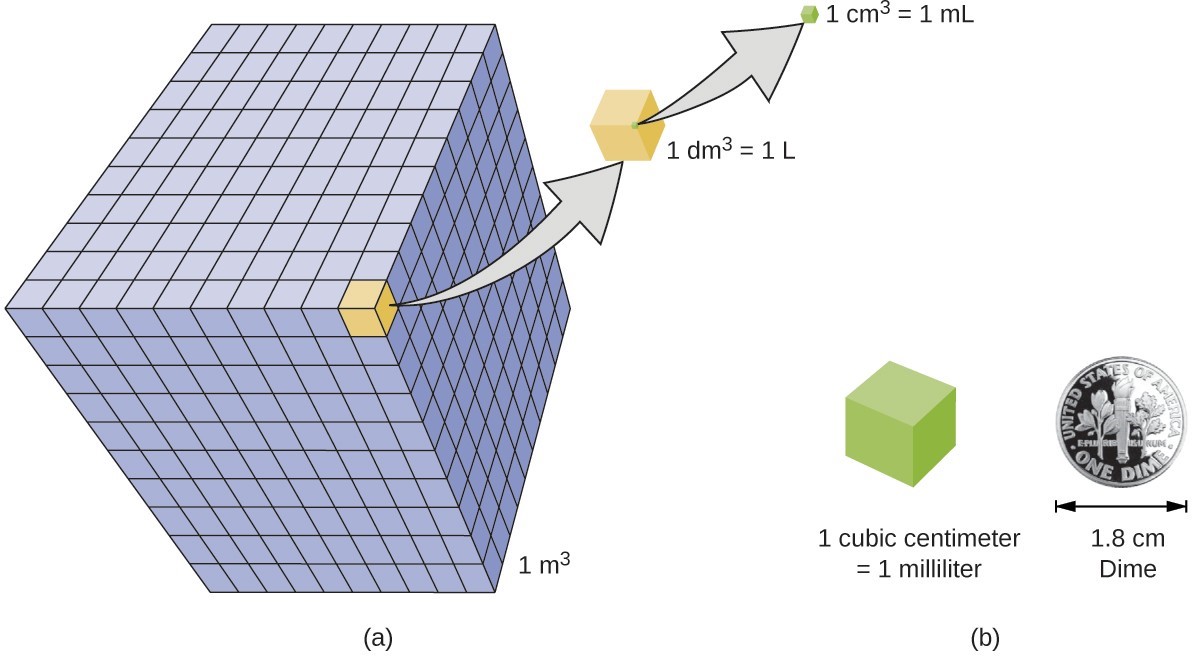
Volume is the measure of the amount of space occupied by an object. The standard SI unit of volume is defined by the base unit of length. The standard volume is a cubic meter (m3), a cube with an edge length of exactly one meter. To dispense a cubic meter of water, we could build a cubic box with edge lengths of exactly one meter. This box would hold a cubic meter of water or any other substance.
A more commonly used unit of volume is derived from the decimeter (0.1 m, or 10 cm). A cube with edge lengths of exactly one decimeter contains a volume of one cubic decimeter (dm3). A liter (L) is the more common name for the cubic decimeter. One liter is about 1.06 quarts.
A cubic centimeter (cm3) is the volume of a cube with an edge length of exactly one centimeter. The abbreviation cc (for cubic centimeter) is often used by health professionals. A cubic centimeter is equivalent to a milliliter (mL) and is 1/1000 of a liter.
Density
We use the mass and volume of a substance to determine its density. Thus, the units of density are defined by the base units of mass and length.
The density of a substance is the ratio of the mass of a sample of the substance to its volume. The SI unit for density is the kilogram per cubic meter (kg/m3). For many situations, however, this as an inconvenient unit, and we often use grams per cubic centimeter (g/cm3) for the densities of solids and liquids, and grams per liter (g/L) for gases. Although there are exceptions, most liquids and solids have densities that range from about 0.7 g/cm3 (the density of gasoline) to 19 g/cm3 (the density of gold). The density of air is about 1.2 g/L. The table below shows the densities of some common substances.
| Densities of Common Substances | ||
|---|---|---|
| Solids | Liquids | Gases (at 25 °C and 1 atm) |
| ice (at 0 °C) 0.92 g/cm3 | water 1.0 g/cm3 | dry air 1.20 g/L |
| oak (wood) 0.60–0.90 g/cm3 | ethanol 0.79 g/cm3 | oxygen 1.31 g/L |
| iron 7.9 g/cm3 | acetone 0.79 g/cm3 | nitrogen 1.14 g/L |
| copper 9.0 g/cm3 | glycerin 1.26 g/cm3 | carbon dioxide 1.80 g/L |
| lead 11.3 g/cm3 | olive oil 0.92 g/cm3 | helium 0.16 g/L |
| silver 10.5 g/cm3 | gasoline 0.70–0.77 g/cm3 | neon 0.83 g/L |
| gold 19.3 g/cm3 | mercury 13.6 g/cm3 | radon 9.1 g/L |
While there are many ways to determine the density of an object, perhaps the most straightforward method involves separately finding the mass and volume of the object, and then dividing the mass of the sample by its volume. In the following example, the mass is found directly by weighing, but the volume is found indirectly through length measurements.
[latex]density=\frac{mass}{volume}[/latex]
EXAMPLE 1.1
Calculation of Density
Gold—in bricks, bars, and coins—has been a form of currency for centuries. In order to swindle people into paying for a brick of gold without actually investing in a brick of gold, people have considered filling the centers of hollow gold bricks with lead to fool buyers into thinking that the entire brick is gold. It does not work, lead is a dense substance, but its density is not as great as that of gold, 19.3 g/cm3. What is the density of lead if a cube of lead has an edge length of 2.00 cm and a mass of 90.7 g?
The density of a substance can be calculated by dividing its mass by its volume. The volume of a cube is calculated by cubing the edge length.
[latex]\text{ volume of lead cube} = 2.00 \text{ cm} \times 2.00 \text{ cm} \times 2.00 \text{ cm} = 8.00 \text{ cm} ^{\text{3}}[/latex]
[latex]\text{ density} = \frac{\text{ mass}}{\text{ volume}} = \frac{90.7 \text{ g}}{8.00 \text{ cm} ^{\text{3}}} = 11.3 \text{ g/cm} ^{\text{3}}[/latex]
(We will discuss the reason for rounding to the first decimal place in the next section.)
Check Your Learning
(a) To three decimal places, what is the volume of a cube (cm3) with an edge length of 0.843 cm?
(b) If the cube in part (a) is copper and has a mass of 5.34 g, what is the density of copper to two decimal places?
(a) 0.599 cm3; (b) 8.91 g/cm3
LINK TO LEARNING
To learn more about the relationship between mass, volume, and density, use this interactive simulator to explore the density of different materials, like wood, ice, brick, and aluminum.
KEY CONCEPTS
Measurements provide quantitative information that is critical in studying and practicing chemistry. Each measurement has an amount, a unit for comparison, and an uncertainty. Measurements can be represented in either decimal or scientific notation. Scientists primarily use SI (International System) units such as meters, seconds, and kilograms, as well as derived units, such as liters (for volume) and g/cm3 (for density). In many cases, it is convenient to use prefixes that yield fractional and multiple units, such as microseconds (10−6 seconds) and megahertz (106 hertz), respectively.
KEY EQUATIONS
- [latex]\text{ density} = \frac{\text{ mass}}{\text{ volume}}[/latex]
CONCEPTUAL PROBLEMS
- Is one liter about an ounce, a pint, a quart, or a gallon?
- Is a meter about an inch, a foot, a yard, or a mile?
- About a yard
- Indicate the SI base units or derived units that are appropriate for the following measurements: (a) the length of a marathon race (26 miles 385 yards), (b) the mass of an automobile, (c) the volume of a swimming pool, (d) the speed of an airplane, (e) the density of gold, (f) the area of a football field, and (g) the maximum temperature at the South Pole on April 1, 1913.
- Indicate the SI base units or derived units that are appropriate for the following measurements: (a) the mass of the moon, (b) the distance from Dallas to Oklahoma City, (c) the speed of sound, (d) the density of air, (e) the temperature at which alcohol boils, (f) the area of the state of Delaware, and (g) the volume of a flu shot or a measles vaccination.
- (a) kilograms, (b) meters, (c) kilometers/second, (d) kilograms/cubic meter, (e) kelvin, (f) square meters, (g) cubic meters
- Give the name and symbol of the prefixes used with SI units to indicate multiplication by the following exact quantities: (a) 103, (b) 10−2, (c) 0.1, (d) 10−3, (e) 1,000,000, (f) 0.000001
- Give the name of the prefix and the quantity indicated by the following symbols that are used with SI base units. (a) c, (b) d, (c) G, (d) k, (e) m, (f) n, (g) p, (h) T
- (a) centi-, × 10−2; (b) deci-, × 10−1; (c) Giga-, × 109; (d) kilo-, × 103; (e) milli-, × 10−3; (f) nano-, × 10−9; (g) pico-, × 10−12; (h) tera-, × 1012
- A large piece of jewelry has a mass of 132.6 g. A graduated cylinder initially contains 48.6 mL water. When the jewelry is submerged in the graduated cylinder, the total volume increases to 61.2 mL. (a) Determine the density of this piece of jewelry. (b) Assuming that the jewelry is made from only one substance, what substance is it likely to be? Explain.
- Visit this PhET density simulation and select the Same Volume Blocks. (a) What are the mass, volume, and density of the yellow block? (b) What are the mass, volume, and density of the red block? (c) List the block colors in order from smallest to largest mass. (d) List the block colors in order from lowest to highest density. (e) How are mass and density related for blocks of the same volume?
- (a) 8.00 kg, 5.00 L, 1.60 kg/L; (b) 2.00 kg, 5.00 L, 0.400 kg/L; (c) red < green < blue < yellow; (d) If the volumes are the same, then the density is directly proportional to the mass.
- Visit this PhET density simulation and select Custom Blocks and then My Block. (a) Enter mass and volume values for the block so that the mass in kg is less than the volume in L. What does the block do? Why? Is this always the case when mass < volume? (b) Enter mass and volume values for the block so that the mass in kg is more than the volume in L. What does the block do? Why? Is this always the case when mass > volume? (c) How would (a) and (b) be different if the liquid in the tank were ethanol instead of water? (d) How would (a) and (b) be different if the liquid in the tank were mercury instead of water?
- Visit this PhET density simulation and select Mystery Blocks. (a) Pick one of the Mystery Blocks and determine its mass, volume, density, and its likely identity. (b) Pick a different Mystery Block and determine its mass, volume, density, and its likely identity. (c) Order the Mystery Blocks from least dense to most dense. Explain.
- (a) (b) Answer is one of the following: A/yellow: mass = 65.14 kg, volume = 3.38 L, density = 19.3 kg/L, likely identity = gold. B/blue: mass = 0.64 kg, volume = 1.00 L, density = 0.64 kg/L, likely identity = apple. C/green: mass = 4.08 kg, volume = 5.83 L, density = 0.700 kg/L, likely identity = gasoline. D/red: mass = 3.10 kg, volume = 3.38 L, density = 0.920 kg/L, likely identity = ice. E/purple: mass = 3.53 kg, volume = 1.00 L, density = 3.53 kg/L, likely identity = diamond. (c) B/blue/apple (0.64 kg/L) < C/green/gasoline (0.700 kg/L) < D/red/ice (0.920 kg/L) < E/purple/diamond (3.53 kg/L) < A/yellow/gold (19.3 kg/L)
Footnotes
- 1 For details, see https://www.nist.gov/pml/weights-and-measures/si-units-mass.
Glossary
- Celsius (°C)
- unit of temperature; water freezes at 0 °C and boils at 100 °C on this scale
- cubic centimeter (cm3 or cc)
- volume of a cube with an edge length of exactly 1 cm
- cubic meter (m3)
- SI unit of volume
- density
- ratio of mass to volume for a substance or object
- kelvin (K)
- SI unit of temperature; 273.15 K = 0 ºC
- kilogram (kg)
- standard SI unit of mass; 1 kg = approximately 2.2 pounds
- length
- measure of one dimension of an object
- liter (L)
- (also, cubic decimeter) unit of volume; 1 L = 1,000 cm3
- meter (m)
- standard metric and SI unit of length; 1 m = approximately 1.094 yards
- milliliter (mL)
- 1/1,000 of a liter; equal to 1 cm3
- second (s)
- SI unit of time
- SI units (International System of Units)
- standards fixed by international agreement in the International System of Units (Le Système International d’Unités)
- unit
- standard of comparison for measurements
- volume
- amount of space occupied by an object
This chapter is an adaptation of the chapter “Measurements” in Chemistry: Atoms First 2e by OpenStax and is licensed under a CC BY 4.0 license.
Access for free at https://openstax.org/books/chemistry-atoms-first-2e/pages/1-introduction
Nuclear Fusion
Nuclear fusion is the process by which two or more atomic nuclei join together to form a single heavier nucleus and large amounts of energy.
LEARNING OBJECTIVES
Describe the electrostatic and strong nuclear forces and how they act to oppose or promote a fusion reaction
KEY TAKEAWAYS
Key Points
- The origin of the energy released in fusion of light elements is due to an interplay of two opposing forces: the nuclear force that draws together protons and neutrons, and the Coulomb force that causes protons to repel each other.
- Fusion reactions of light elements power the stars and produce virtually all elements in a process called nucleosynthesis.
- A substantial energy barrier of electrostatic forces must be overcome before fusion can occur.
Key Terms
- nuclear binding energy: The energy required to split a nucleus of an atom into its component parts.
- nucleon: One of the subatomic particles of the atomic nucleus, i.e. a proton or a neutron.
- nucleosynthesis: Any of several processes that lead to the synthesis of heavier atomic nuclei.
- nuclear force: The force that acts between nucleons and binds protons and neutrons into atomic nuclei; the residual strong force.
- nuclear fusion: A reaction in which two or more atomic nuclei collide at very high speed and join to form a new type of atomic nucleus
Nuclear Fusion
Nuclear fusion is the process by which two or more atomic nuclei join together, or “fuse,” to form a single heavier nucleus. During this process, matter is not conserved because some of the mass of the fusing nuclei is converted to energy, which is released. Fusion is the process that powers active stars, releasing large quantities of energy.
The origin of the energy released in fusion of light elements is due to an interplay of two opposing forces: the nuclear force that draws together protons and neutrons, and the Coulomb force that causes protons to repel each other. The protons are positively charged and repel each other, but they nonetheless stick together, demonstrating the existence of another force referred to as nuclear attraction. This force, called the strong nuclear force, overcomes electric repulsion in a very close range.
Fusion and Strong Nuclear Force
The effect of nuclear force is not observed outside the nucleus, hence the force has a strong dependence on distance; it a short-range force. The same force also pulls the nucleons, or neutrons and protons, together. The nuclear force is stronger than the Coulomb force for atomic nuclei smaller than iron, so building up these nuclei from lighter nuclei by fusion releases the extra energy from the net attraction of these particles. For larger nuclei, no energy is released, since the nuclear force is short-range and cannot continue to act across an even larger atomic nuclei. Therefore, energy is no longer released when such nuclei are made by fusion; instead, energy is absorbed.
Examples of Fusion
Fusion reactions of light elements power the stars and produce virtually all elements in a process called nucleosynthesis. The fusion of lighter elements in stars releases energy, as well as the mass that always accompanies it. For example, in the fusion of two hydrogen nuclei to form helium, seven-tenths of one percent of the mass is carried away from the system in the form of kinetic energy or other forms of energy, like electromagnetic radiation.
Requirements
A substantial energy barrier of electrostatic forces must be overcome before fusion can occur. At large distances, two nuclei repel one another because of the repulsive electrostatic force between their positively charged protons. If two nuclei can be brought close enough together, however, the electrostatic repulsion can be overcome by the attractive nuclear force, which is stronger at close distances.

When a nucleon is added to a nucleus, the nuclear force attracts it to other nucleons, but primarily to its immediate neighbors due to the short range of the force. The nucleons in the interior of a nucleus have more neighboring nucleons than do those on the surface. The binding energy per nucleon generally increases with the size of the nucleus but approaches a limiting value corresponding to that of a nucleus with a diameter of about four nucleons.
The electrostatic force, on the other hand, is dependent upon the inverse-square of the distance between two like-charged particles, so a proton added to a nucleus will feel an electrostatic repulsion from all the other protons in the nucleus. The electrostatic energy per nucleon increases without limit as nuclei get larger due to the electrostatic force.
Fusion Reactors
A fusion reactor is designed to use the thermal energy from nuclear fusion to produce electricity.
LEARNING OBJECTIVES
State the Lawson criterion for a fusion reactor to be viable
KEY TAKEAWAYS
Key Points
- In fusion reactions, two light atomic nuclei fuse together to form a heavier nucleus and release a large amount of energy.
- The basic concept behind any fusion reaction is to bring two light nuclei close enough so the residual strong force (nuclear force) in their nuclei will pull them together.
- The fused nuclei of two smaller atoms form a single nucleus with a slightly smaller mass, providing energy according to [latex]\text{E = mc}^2[/latex].
- Fusion between the nuclei is opposed by the repulsive positive electrical charge common to all nuclei because they contain protons.
Key Terms
- plasma: A state of matter consisting of partially ionized gas.
Reviewing Fusion
Fusion power is the power generated by nuclear fusion processes. In fusion reactions, two light atomic nuclei fuse together to form a heavier nucleus. In doing so, they release a comparatively large amount of energy that arises from the binding energy, creating an increase in temperature of the reactants. To harness fusion power, a fusion reactor must be built to turn the energy released by fusion into electricity.
Harnessing Fusion Power
The term “fusion power” is commonly used to refer to potential commercial production of net usable power from a fusion source, similar to the usage of the term “steam power.” Heat from the fusion reactions is used to operate a steam turbine which in turn drives electrical generators. This is similar to the process used in fossil fuel and nuclear fission power stations.
Conflicting Energies
The basic concept behind any fusion reaction is to bring two or more nuclei close enough so that the residual strong force (nuclear force) in their nuclei will pull them together into one larger nucleus. Fusion between the nuclei is opposed by the repulsive positive electrical charge common to all nuclei because they contain protons. To overcome this electrostatic force, or “Coulomb barrier,” the kinetic energy of the atoms must be increased. The easiest way to do this is to heat the atoms, which has the side effect of stripping their electrons and leaving them as bare nuclei.
Fusion and Energy Concerns
If two light nuclei fuse, they will generally form a single nucleus with a slightly smaller mass than the sum of their original masses; this is not true in every case, though. The difference in mass is released as energy according to Albert Einstein’s mass-energy equivalence formula, [latex]\text{E = mc}^2[/latex]. If the input nuclei are sufficiently massive, the resulting fusion product will be heavier than the sum of the reactants’ original masses, in which case the reaction requires an external source of energy. The dividing line between “light” and “heavy” is iron-56. Above this atomic mass, energy will generally be released by nuclear fission reactions; below this mass, energy will be released by fusion.
In most experiments, the nuclei and electrons are left in a fluid known as a plasma, which is a state of matter that occurs when a gas is heated to extreme temperatures. The temperatures required to provide the nuclei with enough energy to overcome their repulsion is a function of the total charge. Therefore, hydrogen, which has the smallest nuclear charge, fuses at the lowest temperature, and is often used as fuel. Helium has an extremely low mass per nucleon and therefore is energetically favored as a fusion product. As a consequence, most fusion reactions combine isotopes of hydrogen (protium, [latex]^1\text{H}[/latex]; deuterium, [latex]^2\text{H}[/latex] or D; and tritium, [latex]^3 \text{H}[/latex] or T) to form isotopes of helium ([latex]^3\text{He}[/latex] or [latex]^4\text{He}[/latex]) as the fusion end product.
Fuel cycles
The choice of fuel for a fusion reactor is dictated by a term called the Lawson criterion. It was first derived for fusion reactors by John D. Lawson in 1955, and published in 1957. The Lawson criterion is an important general measure of a system that defines the conditions needed for a fusion reactor to reach ignition. Namely, the heating of the plasma by the products of the fusion reactions must be sufficient to maintain the temperature of the plasma against all losses without external power input.
According to the Lawson criterion, the easiest and most immediately promising nuclear reaction for fusion power is:
[latex]_1^2 \text{D} + \ _1^3 \text{T} \rightarrow \ _2^4 \text{He} + \ _0^1 \text{n}[/latex]

Hydrogen-2, called deuterium, is a naturally occurring isotope of hydrogen and is commonly available. The large mass ratio of the hydrogen isotopes makes their separation easy compared to the difficult uranium enrichment process. Hydrogen-3, called tritium, is also an isotope of hydrogen, but it occurs naturally in only negligible amounts due to its half-life of 12.32 years. Consequently, the deuterium-tritium fuel cycle requires the breeding of tritium from lithium using one of the following reactions:
[latex]_0^1 \text{n} + \ _3^6 \text{Li} \rightarrow \ _1^3 \text{T} + \ _2^4 \text{He}[/latex]
[latex]_0^1 \text{n} + \ _3^7 \text{Li} \rightarrow \ _1^3 \text{T} + \ _2^4 \text{He} + \ _0^1 \text{n}[/latex]
The reactant neutron is supplied by the D-T fusion reaction shown earlier. It is the one that has the greatest yield of energy. The reaction with [latex]^6\text{Li}[/latex] is exothermic, providing a small energy gain for the reactor. The reaction with [latex]^7\text{Li}[/latex] is endothermic but does not consume the neutron. At least some [latex]^7\text{Li}[/latex] reactions are required to replace the neutrons lost to absorption by other elements.
The Hydrogen Bomb
The hydrogen bomb is a nuclear weapon that uses a mixture of fission and fusion to produce a massive explosion.
LEARNING OBJECTIVES
Recognize the components of a hydrogen bomb
KEY TAKEAWAYS
Key Points
- A thermonuclear weapon is a nuclear weapon design that uses the heat generated by a fission bomb to compress a nuclear fusion stage.
- The basic principle of the Teller–Ulam configuration, the most common configuration of hydrogen bombs, is the idea that different parts of a thermonuclear weapon can be chained together in “stages,” with the detonation of each stage providing the energy necessary to ignite the next stage.
- The nuclear fusion in an H-bomb releases neutrons much faster than a fission reaction, and these neutrons then bombard the remaining fissile fuel, causing it to undergo fission much more rapidly.
Key Terms
- thermonuclear: Of, or relating to, the fusion of atomic nuclei at high temperatures. Also, relating to the use of atomic weapons based on such fusion.
- fusion: A nuclear reaction in which nuclei combine to form more massive nuclei with the concomitant release of energy and often neutrons.
Thermonuclear Weapons
A thermonuclear weapon is a nuclear weapon designed to use the heat generated by a fission bomb to compress a nuclear fusion stage. This indirectly results in a greatly increased energy yield, i.e., the bomb’s “power.” This type of weapon is referred to as a hydrogen bomb, or H-bomb, because it employs hydrogen fusion. Oddly, in most applications, the majority of its destructive energy comes from uranium fission, not hydrogen fusion alone. The fusion stage in these types of weapons is required in order to efficiently create the large quantities of fission that are characteristic of most thermonuclear weapons.
Features of a Hydrogen Bomb

The essential features of a mature, thermonuclear weapon design, which officially remained secret for nearly three decades, are the following:
- First, the stages of the weapon are separated into a triggering, primary explosive and a much more powerful secondary explosive.
- After this, the secondary explosive is compressed by X-rays coming from the nuclear fission of the primary explosive. This process is called the “radiation implosion” of the secondary explosive.
- Finally, the secondary explosive is heated, after cold compression, by a second fission explosion that occurs inside the secondary explosive.
The most common bomb design that employs these features is called the Teller-Ulam configuration. It should be noted that no hydrogen bomb has ever been used during the course of an actual war. The only two nuclear weapons that have been used were both fission-based.
The most important principle of the Teller–Ulam configuration is the idea that different parts of a thermonuclear weapon can be chained together in “stages,” in which the detonation of each stage provides the energy necessary to ignite the next stage. At a bare minimum, this includes a primary section, which consists of a fission bomb (a “trigger”) and a secondary section which consists of fusion fuel. The energy released by the primary section compresses the secondary through a process called “radiation implosion,” at which point it is heated and undergoes nuclear fusion.
The nuclear fusion releases neutrons much faster than a fission reaction, and these neutrons then bombard the remaining fissile fuel, causing it to undergo fission much more rapidly. As such, the main explosive force for the explosion still arises from a fission reaction, but the neutron source for it arises from fusion.
Due to the staged design, it is thought that a tertiary section, again comprised of fusion fuel, could be added after the first two stages, based on the same principle that governs the secondary. A different design, the AN602 “Tsar Bomba,” is thought to have been a three-stage device.
LICENSES AND ATTRIBUTIONS
CC LICENSED CONTENT, SHARED PREVIOUSLY
- Curation and Revision. Provided by: Boundless.com. License: CC BY-SA: Attribution-ShareAlike
CC LICENSED CONTENT, SPECIFIC ATTRIBUTION
- Nuclear fusion. Provided by: Wikipedia. Located at: http://en.wikipedia.org/wiki/Nuclear_fusion. License: CC BY-SA: Attribution-ShareAlike
- nuclear fusion. Provided by: Wikipedia. Located at: http://en.wikipedia.org/wiki/nuclear%20fusion. License: CC BY-SA: Attribution-ShareAlike
- nucleosynthesis. Provided by: Wiktionary. Located at: http://en.wiktionary.org/wiki/nucleosynthesis. License: CC BY-SA: Attribution-ShareAlike
- nuclear binding energy. Provided by: Wikipedia. Located at: http://en.wikipedia.org/wiki/nuclear%20binding%20energy. License: CC BY-SA: Attribution-ShareAlike
- nucleon. Provided by: Wiktionary. Located at: http://en.wiktionary.org/wiki/nucleon. License: CC BY-SA: Attribution-ShareAlike
- nuclear force. Provided by: Wiktionary. Located at: http://en.wiktionary.org/wiki/nuclear_force. License: CC BY-SA: Attribution-ShareAlike
- Nuclear fusion. Provided by: Wikipedia. Located at: http://en.wikipedia.org/wiki/Nuclear_fusion. License: Public Domain: No Known Copyright
- Fusion power. Provided by: Wikipedia. Located at: http://en.wikipedia.org/wiki/Fusion_power. License: CC BY-SA: Attribution-ShareAlike
- Lawson criterion. Provided by: Wikipedia. Located at: http://en.wikipedia.org/wiki/Lawson_criterion. License: CC BY-SA: Attribution-ShareAlike
- plasma. Provided by: Wiktionary. Located at: http://en.wiktionary.org/wiki/plasma. License: CC BY-SA: Attribution-ShareAlike
- Nuclear fusion. Provided by: Wikipedia. Located at: http://en.wikipedia.org/wiki/Nuclear_fusion. License: Public Domain: No Known Copyright
- Nuclear%252520fusion. Provided by: Wikipedia. Located at: http://en.wikipedia.org/wiki/Nuclear_fusion. License: Public Domain: No Known Copyright
- Hydrogen bomb. Provided by: Wikipedia. Located at: http://en.wikipedia.org/wiki/Hydrogen_bomb. License: CC BY-SA: Attribution-ShareAlike
- fusion. Provided by: Wiktionary. Located at: http://en.wiktionary.org/wiki/fusion. License: CC BY-SA: Attribution-ShareAlike
- thermonuclear. Provided by: Wiktionary. Located at: http://en.wiktionary.org/wiki/thermonuclear. License: CC BY-SA: Attribution-ShareAlike
- Nuclear fusion. Provided by: Wikipedia. Located at: http://en.wikipedia.org/wiki/Nuclear_fusion. License: Public Domain: No Known Copyright
- Nuclear%252520fusion. Provided by: Wikipedia. Located at: http://en.wikipedia.org/wiki/Nuclear_fusion. License: Public Domain: No Known Copyright
- File:Teller-Ulam device 3D.svg – Wikipedia, the free encyclopedia. Provided by: Wikipedia. Located at: http://en.wikipedia.org/w/index.php?title=File:Teller-Ulam_device_3D.svg&page=1. License: Public Domain: No Known Copyright
measure of one dimension of an object
standard metric and SI unit of length; 1 m = approximately 1.094 yards
standard SI unit of mass; 1 kg = approximately 2.2 pounds
SI unit of temperature; 273.15 K = 0 ºC
unit of temperature; water freezes at 0 °C and boils at 100 °C on this scale
SI unit of time
amount of space occupied by an object
SI unit of volume
(also, cubic decimeter) unit of volume; 1 L = 1,000 cm3
1/1,000 of a liter; equal to 1 cm3
volume of a cube with an edge length of exactly 1 cm
ratio of mass to volume for a substance or object
standards fixed by international agreement in the International System of Units (Le Système International d’Unités)
standard of comparison for measurements

