60 Entropy

Microstates and Entropy

Energy can be shared between microstates of a system. With more available microstates, the entropy of a system increases.

Entropy of the Playroom: Andrew Vanden Heuvel explores the concept of entropy while cleaning the playroom.

Second Law of Thermodynamics

In classical thermodynamics, the second law of thermodynamics states that the entropy of an isolated system always increases or remains constant. Therefore, entropy is also a measure of the tendency of a process, such as a chemical reaction, to be entropically favored or to proceed in a particular direction. It determines that thermal energy always flows spontaneously from regions of higher temperature to regions of lower temperature, in the form of heat.

These processes reduce the state of order of the initial systems. As a result, entropy (denoted by S) is an expression of disorder or randomness. Thermodynamic entropy has the dimension of energy divided by temperature, which has a unit of joules per kelvin (J/K) in the International System of Units.

The interpretation of entropy is the measure of uncertainty, which remains about a system after its observable macroscopic properties, such as temperature, pressure, and volume, have been taken into account. For a given set of macroscopic variables, the entropy measures the degree to which the probability of the system is spread out over different possible microstates. In contrast to the macrostate, which characterizes plainly observable average quantities (temperature, for example), a microstate specifies all molecular details about the system, including the position and velocity of every molecule. With more available microstates, the entropy of a system increases. This is the basis of an alternative (and more fundamental) definition of entropy:

[latex]\text{S} = \text{kln} \Omega[/latex]

in which k is the Boltzmann constant (the gas constant per molecule, [latex]1.38 \times 10^{-23} \frac{\text{J}}{\text{K}}[/latex]) and Ω (omega) is the number of microstates that correspond to a given macrostate of the system. The more such microstates, the greater is the probability of the system being in the corresponding macrostate. For any physically realizable macrostate, the quantity Ω is an unimaginably large number.

Even though it is beyond human comprehension to compare numbers that seem to verge on infinity, the thermal energy contained in actual physical systems manages to discover the largest of these quantities with no difficulty at all, quickly settling in to the most probable macrostate for a given set of conditions.

Phase changes and entropy

In terms of energy, when a solid becomes a liquid or a liquid a vapor, kinetic energy from the surroundings is changed to ‘potential energy‘ in the substance (phase change energy). This energy is released back to the surroundings when the surroundings become cooler than the substance’s boiling or melting temperature, respectively. Phase-change energy increases the entropy of a substance or system because it is energy that must be spread out in the system from the surroundings so that the substance can exist as a liquid or vapor at a temperature above its melting or boiling point. Therefore, the entropy of a solid is less than the entropy of a liquid, which is much less than the entropy of a gas:

S_solid < S_liquid << S_gas

Changes in Energy

The concept of entropy can be described qualitatively as a measure of energy dispersal at a specific temperature.

Entropy

The concept of entropy evolved in order to explain why some processes (permitted by conservation laws) occur spontaneously while their time reversals (also permitted by conservation laws) do not; systems tend to progress in the direction of increasing entropy. For isolated systems, entropy never decreases. This fact has several important consequences in science: first, it prohibits “perpetual motion” machines; and second, it implies the arrow of entropy has the same direction as the arrow of time. Increases in entropy correspond to irreversible changes in a system. This is because some energy is expended as heat, limiting the amount of work a system can do.

In classical thermodynamics the entropy is interpreted as a state function of a thermodynamic system. A state function is a property depending only on the current state of the system, independent of how that state came to be achieved. The state function has the important property that in any process where the system gives up energy ΔE, and its entropy falls by ΔS, a quantity at least TR ΔS of that energy must be given up to the system’s surroundings as unusable heat (TR is the temperature of the system’s external surroundings). Otherwise the process will not go forward. The entropy of a system is defined only if it is in thermodynamic equilibrium. In a thermodynamic system, pressure, density, and temperature tend to become uniform over time because this equilibrium state has a higher probability (more possible combinations of microstates) than any other.

Ice Water and Entropy

For example, consider ice water in a glass. The difference in temperature between a warm room (the surroundings) and a cold glass of ice and water (the system and not part of the room) begins to equalize. This is because the thermal energy from the warm surroundings spreads to the cooler system of ice and water. Over time, the temperature of the glass and its contents and the temperature of the room become equal. The entropy of the room decreases as some of its energy is dispersed to the ice and water. However, the entropy of the system of ice and water has increased more than the entropy of the surrounding room has decreased.

In an isolated system such as the room and ice water taken together, the dispersal of energy from warmer to cooler always results in a net increase in entropy. Thus, when the “universe” of the room and ice water system has reached a temperature equilibrium, the entropy change from the initial state is at a maximum. The entropy of the thermodynamic system is a measure of how far the equalization has progressed.

The second law of thermodynamics shows that in an isolated system internal portions at different temperatures will tend to adjust to a single uniform temperature and thus produce equilibrium. A recently developed educational approach avoids ambiguous terms and describes such spreading out of energy as dispersal. Physical chemist Peter Atkins, for example, who previously wrote of dispersal leading to a disordered state, now writes that “spontaneous changes are always accompanied by a dispersal of energy”.

Standard Entropy

The standard entropy of a substance (its entropy at 1 atmospheric pressure) helps determine if a reaction will take place spontaneously.

Defining Standard Entropy

The standard entropy of a substance is its entropy at 1 atm pressure. The values found in the table are normally those for 298K, and are expressed in units of [latex]\frac{\text{J}}{\text{K} \cdot \text{mole}}[/latex]. Some typical standard entropy values for gaseous substances include:

• [latex]\text{He}[/latex]: [latex]126 \ \frac{\text{J}}{\text{K} \cdot \text{mole}}[/latex]
• [latex]\text{Xe}[/latex]: [latex]170 \ \frac{\text{J}}{\text{K} \cdot \text{mole}}[/latex]
• [latex]\text{O}_2[/latex]: [latex]205 \ \frac{\text{J}}{\text{K} \cdot \text{mole}}[/latex]
• [latex]\text{CO}_2[/latex]: [latex]213 \ \frac{\text{J}}{\text{K} \cdot \text{mole}}[/latex]
• [latex]\text{H}_2\text{O} (g)[/latex]: [latex]187 \ \frac{\text{J}}{\text{K} \cdot \text{mole}}[/latex]

Scientists conventionally set the energies of formation of elements in their standard states to zero. Entropy, however, measures not energy itself, but its dispersal among the various quantum states available to accept it, and these exist even in pure elements.

Comparing Entropy

It is apparent that entropies generally increase with molecular weight. For the noble gases, this is a direct reflection of the principle that translational quantum states are more closely packed in heavier molecules, allowing them to be occupied. The entropies of the diatomic and polyatomic molecules show the additional effects of rotational quantum levels.

Entropy in Solids

The entropies of solid elements are strongly influenced by the type of atom packing in the solid. Although both diamond and graphite are types of carbon, their entropies differ significantly. Graphite, which is built up of loosely-bound stacks of hexagonal sheets, soaks up thermal energy twice as well as diamond. The carbon atoms in diamond are tightly locked in a three-dimensional lattice, preventing them from vibrating around their equilibrium positions.

There is an inverse correlation between the hardness of a solid and its entropy. For example, sodium, which can be cut with a knife, has almost twice the entropy of iron, which cannot be easily cut. These trends are consistent with the principle that the more disordered a substance, the greater its entropy.

Entropy in Gases and Liquids

Gases, which serve as efficient vehicles for spreading thermal energy over a large volume of space, have much higher entropies than condensed phases. Similarly, liquids have higher entropies than solids because molecules in a liquid can interact in many different ways.

The standard entropy of reaction helps determine whether the reaction will take place spontaneously. According to the second law of thermodynamics, a spontaneous reaction always results in an increase in total entropy of the system and its surroundings:

[latex]\Delta \text{S}_\text{total} = \Delta \text{S}_\text{system} + \Delta \text{S}_\text{surroundings}[/latex]

The Third Law of Thermodynamics and Absolute Energy

The third law of thermodynamics states that the entropy of a system approaches a constant value as the temperature approaches absolute zero.

The Basic Law

The third law of thermodynamics states that the entropy of a system approaches a constant value as the temperature approaches zero. The entropy of a system at absolute zero is typically zero, and in all cases is determined only by the number of different ground states it has. Specifically, the entropy of a pure crystalline substance at absolute zero temperature is zero.

At zero temperature the system must be in a state with the minimum thermal energy. This statement holds true if the perfect crystal has only one state with minimum energy. Entropy is related to the number of possible microstates according to [latex]\text{S} = \text{k}_\text{Bln} (\Omega)[/latex], where [latex]\text{S}[/latex] is the entropy of the system, [latex]\text{k}_\text{B}[/latex] is Boltzmann’s constant, and [latex]\Omega[/latex] is the number of microstates (e.g. possible configurations of atoms).

At absolute zero there is only 1 microstate possible ([latex]\Omega = 1[/latex]) and [latex]\text{ln(1) = 0}[/latex]. A more general form of the third law applies to systems such as glasses that may have more than one minimum energy state: the entropy of a system approaches a constant value as the temperature approaches zero. The constant value (not necessarily zero) is called the residual entropy of the system. Physically, the law implies that it is impossible for any procedure to bring a system to the absolute zero of temperature in a finite number of steps.

Absolute Entropy

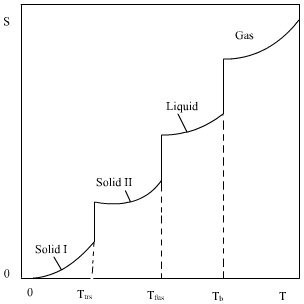
The entropy determined relative to this point (absolute zero) is the absolute entropy. Mathematically, the absolute entropy of any system at zero temperature is the natural log of the number of ground states times Boltzmann’s constant [latex]\text{k}_\text{B}[/latex]. The entropy of a perfect crystal lattice is zero, provided that its ground state is unique (only one), because [latex]\text{ln(1) = 0}[/latex].

An example of a system which does not have a unique ground state is one containing half-integer spins, for which there are two degenerate ground states. For such systems, the entropy at zero temperature is at least [latex]\text{ln(2)k}_\text{B}[/latex], which is negligible on a macroscopic scale.

In addition, glasses and solid solutions retain large entropy at absolute zero, because they are large collections of nearly degenerate states, in which they become trapped out of equilibrium. For the entropy at absolute zero to be zero, the magnetic moments of a perfectly ordered crystal must themselves be perfectly ordered. Only ferromagnetic, antiferromagnetic, and diamagnetic materials can satisfy this condition. Materials that remain paramagnetic at absolute zero, by contrast, may have many nearly-degenerate ground states, as in a spin glass, or may retain dynamic disorder, as is the case in a spin liquid.