49 Molecular Geometry

Table of Geometries

The VSEPR theory detremines molecular geometries (linear, trigonal, trigonal bipyramidal, tetrahedral, and octahedral).

VSEPR Model

The valence shell electron pair repulsion (VSEPR) model focuses on the bonding and nonbonding electron pairs present in the outermost (valence) shell of an atom that connects with two or more other atoms.

Fundamentally, the VSEPR model theorizes that these regions of negative electric charge will repel each other, causing them (and the chemical bonds that they form) to stay as far apart as possible. Therefore, the two electron clouds contained in a simple triatomic molecule [latex]\text{AX}_2[/latex] will extend out in opposite directions. An angular separation of 180° places the two bonding orbitals as far away from each other as possible; we therefore expect the two chemical bonds to extend in opposite directions, producing a linear molecule.

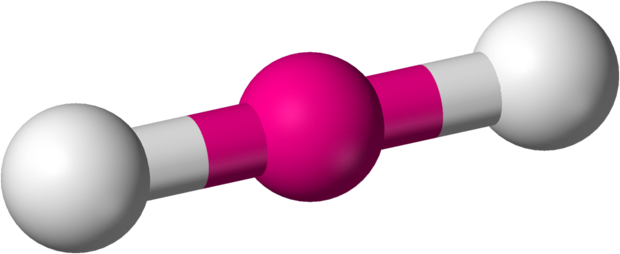
If the central atom also contains one or more pairs of non-bonding electrons, these additional regions of negative charge will behave much like those associated with the bonded atoms. The orbitals containing the various bonding and non-bonding pairs in the valence shell will extend out from the central atom in directions that minimize their mutual repulsions. If the central atom possesses partially occupied d-orbitals, it may be able to accommodate five or six electron pairs, forming what is sometimes called an “expanded octet.”

Molecular Geometries

Molecular geometries (linear, trigonal, tetrahedral, trigonal bipyramidal, and octahedral) are determined by the VSEPR theory. A table of geometries using the VSEPR theory can facilitate drawing and understanding molecules. The table of molecular geometries can be found in the first figure. The second figure serves as a visual aid for the table.

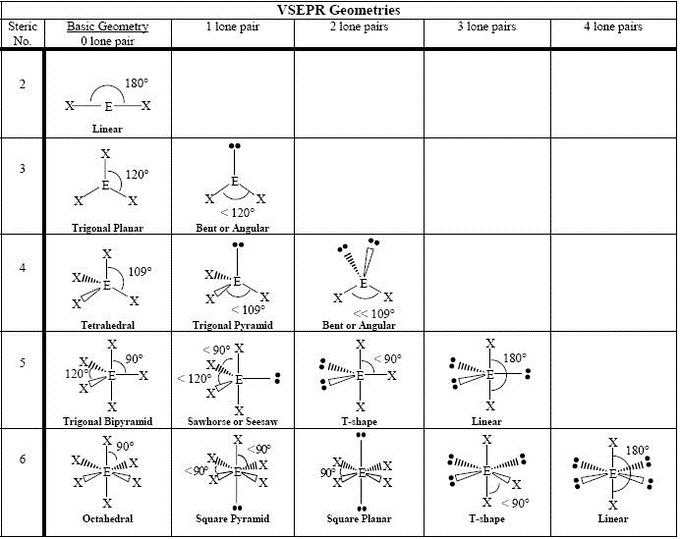
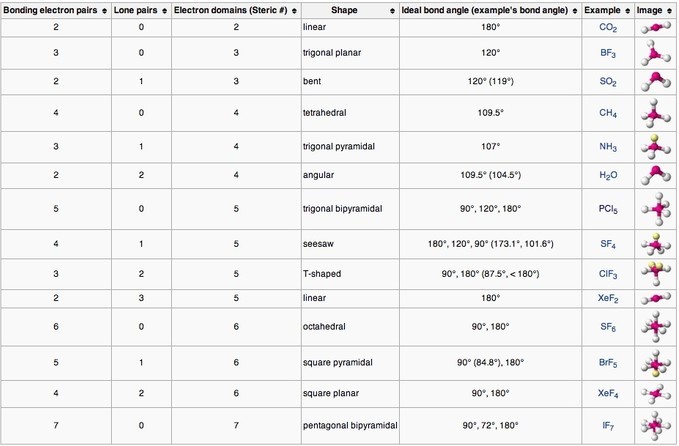
How to Determine Molecular Geometry – YouTube: This video describes one method for quickly finding the major geometrical shapes for simple molecules.

Molecular Geometries

The VSEPR theory describes five main shapes of simple molecules: linear, trigonal planar, tetrahedral, trigonal bipyramidal, and octahedral.

AXE Method

Another way of looking at molecular geometries is through the “AXE method” of electron counting. A in AXE represents the central atom and always has an implied subscript one; X represents the number of sigma bonds between the central and outside atoms (multiple covalent bonds—double, triple, etc.— count as one X); and E represents the number of lone electron pairs surrounding the central atom. The sum of X and E, known as the steric number, is also associated with the total number of hybridized orbitals used by valence bond theory. VSEPR uses the steric number and distribution of X’s and E’s to predict molecular geometric shapes.

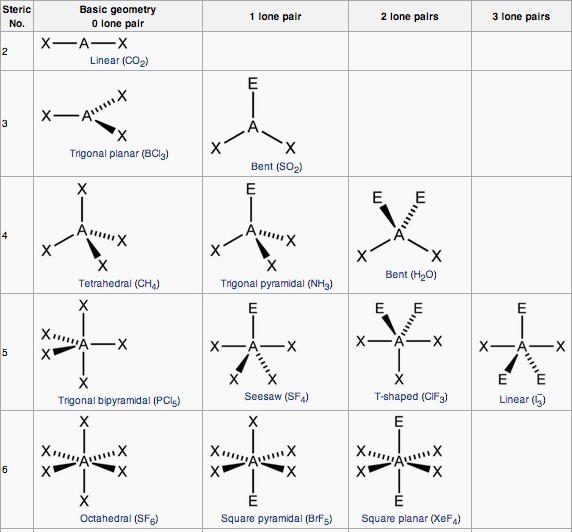
Note that the geometries are named according to the atomic positions only, not the electron arrangement.

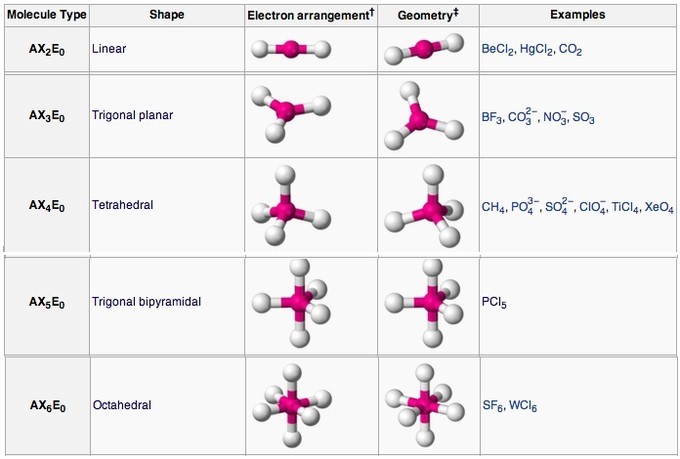
Main geometries (without lone pairs of electrons):

Linear

In a linear model, atoms are connected in a straight line, and a bond angle is simply the geometric angle between two adjacent bonds. A simple triatomic molecule of the type [latex]\text{AX}_2[/latex] has its two bonding orbitals 180° apart. Examples of triatomic molecules for which VSEPR theory predicts a linear shape include [latex]\text{BeCl}_2[/latex] (which does not possess enough electrons to conform to the octet rule) and [latex]\text{CO}_2[/latex]. When writing out the electron dot formula for carbon dioxide, notice that the C-O bonds are double bonds; this makes no difference to VSEPR theory. The central carbon atom is still joined to two other atoms. The electron clouds that connect the two oxygen atoms are 180° apart.

Trigonal Planar

Molecules with the trigonal planar shape are triangular and in one plane, or flat surface. An [latex]\text{AX}_3[/latex] molecule such as [latex]\text{BF}_3[/latex] has three regions of electron density extending out from the central atom. The repulsion between these will be at a minimum when the angle between any two is 120^o.

Tetrahedral

Tetra- signifies four, and -hedral relates to a face of a solid; “tetrahedral” literally means “having four faces. ” This shape is found when there are four bonds all on one central atom, with no lone electron pairs. In accordance with the VSEPR theory, the bond angles between the electron bonds are 109.5^o. An example of a tetrahedral molecule is methane [latex]( \text{CH}_4 )[/latex]. The four equivalent bonds point in four geometrically equivalent directions in three dimensions, corresponding to the four corners of a tetrahedron centered on the carbon atom.

A trigonal bipyramidal shape forms when a central atom is surrounded by five atoms in a molecule. In the geometry, three atoms are in the same plane with bond angles of 120°; the other two atoms are on opposite ends of the molecule. Some elements in Group 15 of the periodic table form compounds of the type [latex]\text{AX}_5[/latex]; examples include [latex]\text{PCl}_5[/latex] and [latex]\text{AsF}_5[/latex].

Octahedral

Octa- signifies eight, and -hedral relates to a face of a solid, so “octahedral” literally means “having eight faces.” The bond angles are all 90°, and just as four electron pairs experience minimum repulsion when they are directed toward the corners of a tetrahedron, six electron pairs try to point toward the corners of an octahedron. An example of an octahedral molecule ([latex]\text{AX}_6[/latex]) is sulfur hexafluoride ([latex]\text{SF}_6[/latex]).

https://lab.concord.org/embeddable.html#interactives/jsmol/electron-geometry.json

Interactive: Electron Geometry: Molecules assume different shapes due to patterns of shared and unshared electrons. In these examples all electrons affecting the shape of the molecules are shared in the covalent bonds holding the atoms together to form the molecules.

Lone Electron Pairs

Nonbonding electrons are in orbitals that occupy space, repel the other orbitals, and change a molecule’s shape.

Molecular Geometries with Lone Pair Electrons

So far, we have only discussed geometries without any lone pairs of electrons. As you likely noticed in the table of geometries and the AXE method, adding lone pairs changes a molecule ‘s shape. We mentioned before that if the central atom also contains one or more pairs of nonbonding electrons, these additional regions of negative charge will behave much like those associated with the bonded atoms. The orbitals containing the various bonding and nonbonding pairs in the valence shell will extend out from the central atom in directions that minimize their mutual repulsions.

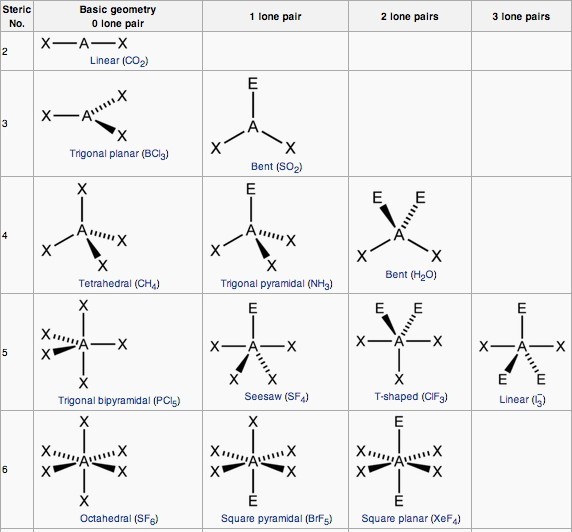
Coordination Number and the Central Atom

Coordination number refers to the number of electron pairs that surround a given atom, often referred to as the central atom. The geometries of molecules with lone pairs will differ from those without lone pairs, because the lone pair looks like empty space in a molecule. Both classes of geometry are named after the shapes of the imaginary geometric figures (mostly regular solid polygons) that would be centered on the central atom and have an electron pair at each vertex.

In the water molecule ([latex]\text{AX}_2\text{E}_2[/latex]), the central atom is [latex]\text{O}[/latex], and the Lewis electron dot formula predicts that there will be two pairs of nonbonding electrons. The oxygen atom will therefore be tetrahedrally coordinated, meaning that it sits at the center of the tetrahedron. Two of the coordination positions are occupied by the shared electron-pairs that constitute the O–H bonds, and the other two by the non-bonding pairs. Therefore, although the oxygen atom is tetrahedrally coordinated, the bonding geometry (shape) of the [latex]\text{H}_2\text{O}[/latex] molecule is described as bent.

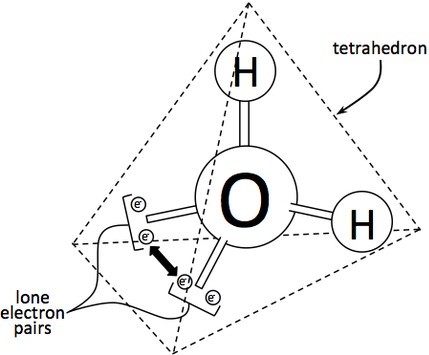
The Repulsive Effect of the Lone Pair Electrons

There is an important difference between bonding and non-bonding electron orbitals. Because a nonbonding orbital has no atomic nucleus at its far end to draw the electron cloud toward it, the charge in such an orbital will be concentrated closer to the central atom; as a consequence, nonbonding orbitals exert more repulsion on other orbitals than do bonding orbitals. In [latex]\text{H}_2\text{O}[/latex], the two nonbonding orbitals push the bonding orbitals closer together, making the H–O–H angle 104.5° instead of the tetrahedral angle of 109.5°.

The electron-dot structure of [latex]\text{NH}_3[/latex] places one pair of nonbonding electrons in the valence shell of the nitrogen atom. This means that there are three bonded atoms and one lone pair for a coordination number of four around the nitrogen, the same as occurs in [latex]\text{H}_2\text{O}[/latex].

We can therefore predict that the three hydrogen atoms will lie at the corners of a tetrahedron centered on the nitrogen atom. The lone pair orbital will point toward the fourth corner of the tetrahedron, but since that position will be vacant, the [latex]\text{NH}_3[/latex] molecule itself cannot be tetrahedral; instead, it assumes a pyramidal shape, more specifically, that of a trigonal pyramid (a pyramid with a triangular base). The hydrogen atoms are all in the same plane, with the nitrogen outside of the plane. The non-bonding electrons push the bonding orbitals together slightly, making the H–N–H bond angles about 107°.

In 5-coordinated molecules containing lone pairs, these non-bonding orbitals (which are closer to the central atom and thus more likely to be repelled by other orbitals) will preferentially reside in the equatorial plane. This will place them at 90° angles with respect to no more than two axially-oriented bonding orbitals. We can therefore predict that an [latex]\text{AX}_4\text{E}[/latex] molecule (one in which the central atom A is coordinated to four other atoms X and to one nonbonding electron pair) such as [latex]\text{SF}_4[/latex] will have a “see-saw” shape.

Substituting nonbonding pairs for bonded atoms reduces the triangular bipyramid coordination to even simpler molecular shapes.

https://lab.concord.org/embeddable.html#interactives/jsmol/unshared-electrons.json

Interactive: Unshared Electrons and the “Bent” Shape: Use the 3D model to see how unshared electrons repel those that are shared in the bonds between hydrogen and oxygen, causing the molecule to have a “bent” shape.