CHAPTER 5: LINEAR EQUATIONS IN ONE VARIABLE
5-3: Properties of Equality
Introduction
Properties that allow us to manipulate an algebraic equation without changing the solution of the equation are called properties of equality. We can use properties of equality to write equivalent equations that look different from the original equation but have exactly the same solution as the original equation. Conditional linear equations in one variable always have exactly one solution. Given a linear equation, we can use the properties of equality to help determine the solution of the equation.
 Properties of Equality
Properties of Equality
The properties of equality can be used to solve conditional linear equations in one variable. The first property is the property of symmetry, which says that if ![]() , then
, then ![]() . So, if we know that
. So, if we know that ![]() , the property of symmetry tells us that
, the property of symmetry tells us that ![]() . This may appear to be trivial, but it has important ramifications in higher level mathematics.
. This may appear to be trivial, but it has important ramifications in higher level mathematics.
Explore 1 – Subtraction property of equality
Brendon and Julie are packing up for a trip. They want to know the weight of their luggage. Julie picks up a piece of luggage and stands on a scale. It reads 188 pounds. Julie then stands on the scale again without the piece of luggage and it reads 145 pounds.
- Julie claims that the weight of the luggage is 188 lb – 145 lb = 43 lb. Do you agree? Explain your reasoning
Solution
Yes. It is correct. Since Julie and the luggage together weigh 188 pounds and Julie weighs 145 pounds, we can subtract Julie’s weight to get the weight of the luggage: 188 lb – 145 lb = 43 lb.
- Julie writes an equation to explain what she just did. She defines
 to represent the weight of the luggage. The equation she writes is
to represent the weight of the luggage. The equation she writes is 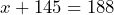 : the weight of the luggage plus the weight of Julie equals the weight of the luggage and Julie. To solve for
: the weight of the luggage plus the weight of Julie equals the weight of the luggage and Julie. To solve for  , Julie wants an equivalent equation where
, Julie wants an equivalent equation where  is on one side of the equation by itself. On the left side of the equation, 145 is added to
is on one side of the equation by itself. On the left side of the equation, 145 is added to  , so Julie removes 145 by subtracting 145 from both sides of the equation:
, so Julie removes 145 by subtracting 145 from both sides of the equation: 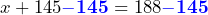 which simplifies to
which simplifies to 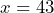 . Is it valid to subtract 145 from both sides of the equation? Explain your reasoning.
. Is it valid to subtract 145 from both sides of the equation? Explain your reasoning.
Solution
Yes, it is valid. Since both sides of the equation are equal, both sides will still be equal if we subtract the same amount from both sides of the equation.
Subtracting the same number to both sides of an equation results in an equivalent equation with the same solution as the original equation.
Explore 2 – Addition property of equality
In a fast-food restaurant, Brendon purchases a meal that costs him $8.23. Brendon wants to give the cashier enough money so that he can get a $5 bill back.
- Brendon writes the equation
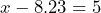 . What does the variable
. What does the variable  represent? Explain your reasoning.
represent? Explain your reasoning.
Solution
The variable ![]() represents the money Brendon should pay in order to get a $5 bill back.
represents the money Brendon should pay in order to get a $5 bill back.
- In an attempt to solve for
 , Brendon adds 8.23 to both sides of the equation:
, Brendon adds 8.23 to both sides of the equation: 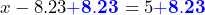 which simplifies to
which simplifies to 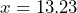 . Is it true that the cashier will return a $5 bill to Brendon if Brendon gives the cashier $13.23 to pay for his meal. Explain your reasoning.
. Is it true that the cashier will return a $5 bill to Brendon if Brendon gives the cashier $13.23 to pay for his meal. Explain your reasoning.
Solution
Yes, it is true. If Brendan pays $13.23, the cashier should only take $8.23 from Brendon and return the change to Brendon. The change is $13.23 – $8.23 = $5.
- Is it valid to add 8.23 to both sides of the equation?
Solution
Yes, it is valid. The equation shows that the amount on the left side is equal to the amount of the right side, adding the same number to both sides of the equation will not change the value of ![]() and will not change the equality relation.
and will not change the equality relation.
Adding the same number to both sides of an equation results in an equivalent equation with the same solution as the original equation.
Explore 3 – Division property of equality
Nadia attended therapy sessions and paid a total of $128 for four sessions. How much did each session cost?
- Write an equation to model the total cost of four sessions with respect to the price of each session.
Solution
First we have to define a variable to represent the cost of a single session: Let ![]() the cost of a single session.
the cost of a single session.
Since 4 sessions cost $128, then 4 times the cost of one session must equal $128: ![]()
- Nadia divides both sides of the equation by 4, and gets $32 as the price of each session. What does it mean to divide each side of the equation by 4?
Solution
![]() simplifies to
simplifies to ![]()
On the left side of the equation, dividing the total price of four sessions (i.e., ![]() ) by 4, we get the price of each session. (i.e.,
) by 4, we get the price of each session. (i.e., ![]() ).
).
On the right side of the equation, dividing the total price $128 by 4, we get the price of each session, $32.
- Is it valid to divide both sides of the equation by 4? Explain your reasoning.
Solution
Yes, it is valid. The equation shows that the amount on the left side is equal to the amount on the right side, dividing the same amount by the same number will not change the value of ![]() and will not change the equality relation.
and will not change the equality relation.
Dividing both sides of an equation by the same number results in an equivalent equation with the same solution as the original equation.
Explore 4 – Multiplication property of equality
Saar and her family are embarking on a long road trip. There is 3/4 of a tank of gas in the car. Saar goes to a gas station and spends $23 to fill up the gas tank. Saar writes the equation ![]() to model the relation between the gas required to fill up the gas tank and the price it cost, $23.
to model the relation between the gas required to fill up the gas tank and the price it cost, $23.
- What does
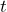 represent? Where does 1/4 come from? What does
represent? Where does 1/4 come from? What does 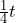 mean?
mean?
Solution
![]() the cost of fuel for a full tank of gas
the cost of fuel for a full tank of gas
The tank is ![]() full, so Saar needs to buy
full, so Saar needs to buy ![]() tank of gas to fill the tank:
tank of gas to fill the tank: ![]()
![]() the cost of a quarter tank of gas
the cost of a quarter tank of gas
- Saar multiplies both sides of the equation by 4:
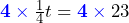 which simplifies to
which simplifies to 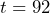 . Is it valid to do so? Explain your reasoning.
. Is it valid to do so? Explain your reasoning.
Solution
Yes, it is valid. Since the amount on the left side of the equation (i.e., the cost for 1/4 tank of fuel) is equal to the amount on the right side (i.e., the price paid for the 1/4 tank of fuel), we can divide both sides by the same number as doing so will not change the value of ![]() and will not change the equality relation.
and will not change the equality relation.
Multiplying both sides of an equation by the same number results in an equivalent equation with the same solution as the original equation.
- What does the solution of the equation
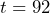 mean?
mean?
Solution
![]() was defined as the cost of fuel for a full tank of gas. So, the solution
was defined as the cost of fuel for a full tank of gas. So, the solution ![]() means the cost of fuel for a full tank of gas is $92.
means the cost of fuel for a full tank of gas is $92.
Properties of Equality*
*These are not the only properties of equality, but these are the ones we need to solve linear equations.
- Symmetry: If
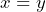 , then
, then 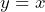 .
.
Switching the sides of an equation does not change the solution of the equation.
- Addition and subtraction: If
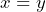 , then
, then 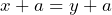 and
and 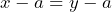
We may add or subtract the same term to both sides of an equation. The result will be an equivalent equation.
- Multiplication and division: If
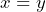 , then
, then 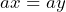 for all
for all 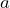 and
and 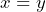 for all
for all 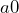 .
.
We may multiply or divide the same amount to both sides of an equation. The result will be an equivalent equation.
Example
In a math class, in order to illustrate equality, a teacher had a balance scale on the front desk with small colored wooden blocks on each side. On the left side she had 3 green blocks and two red blocks. On the right side, she has eight red blocks. The scale is balanced. Suppose each red block has a weight of 1 and we define ![]() to represent the weight of a green block.
to represent the weight of a green block.
- Draw a picture that represents the balance scale.
Solution

- Write an equation that represents the balanced scale.
Solution
![]()
“One property of equality,” she demonstrated, “is that we can take off blocks from each side and the scale remains balanced.” She removed 2 red blocks from each side, and the scale remained balanced.
- Write an equation that represents what she did to the original equation, then simplify it.
Solution
![]() which simplifies to
which simplifies to ![]()
- How would this instructor illustrate the multiplication property of equality?
Solution
Multiplication is repeated addition. For example, ![]() . So to multiply either side of an equation by 3, the teacher would add exactly what is on that side so there three sets of the original amount.
. So to multiply either side of an equation by 3, the teacher would add exactly what is on that side so there three sets of the original amount.
For example if the scale is balanced with 1 red block and 2 green blocks, and we want to multiply by 3, the teacher would add 2 more red blocks to the left side to get a total of 3 red blocks. On the right side she would add 2 more sets of 2 green blocks to have a total of 6 green blocks.

- When would you use the subtraction property of equality? Explain your reasoning.
Show/Hide Answer
When there is variable plus a number in an equation, you may use the property to remove the number to isolate the variable and solve the equation.
- When do you use the division property of equality? Explain your reasoning.
Show/Hide Answer
When there is a variable multiplied by a number in an equation, you may use the property to simplify the number to 1 to isolate the variable and solve the equation.
Practice Exercises
- Francesco is explaining properties of equality to his classmate. He states that, “If you have the equation
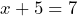 , then by subtracting 5 from both sides of the equation, we can determine that x = 2.” Is Francesco correct? If so, what property of equality is he using? If not, how would you change his statement to be correct?
, then by subtracting 5 from both sides of the equation, we can determine that x = 2.” Is Francesco correct? If so, what property of equality is he using? If not, how would you change his statement to be correct? - Bridget goes to the store and purchases 30 reams of paper. Her total before taxes is $90. Defining
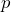 as a variable that represents the cost of each ream of paper, an equation that represents this situation is
as a variable that represents the cost of each ream of paper, an equation that represents this situation is 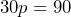 . a) Explain, in words, how to solve this equation? b) What property of equality do you use? c) Why does this property of equality work?
. a) Explain, in words, how to solve this equation? b) What property of equality do you use? c) Why does this property of equality work? - Hayley has $1200 saved to buy a new tv. She knows she will have to pay tax on the tv so she is trying to figure out the maximum price of tv she can afford. The tax rate is 6.75% and she has defined
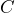 to represent the total cost, and
to represent the total cost, and 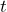 to be the price of the tv. She writes the equation
to be the price of the tv. She writes the equation 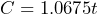 . a) Is this the correct equation that relates total cost to the price of the tv? Explain your reasoning. b) What value should she substitute for
. a) Is this the correct equation that relates total cost to the price of the tv? Explain your reasoning. b) What value should she substitute for 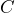 ? Write the equation with this substitution. c) What property of equality should she use to solve the equation for
? Write the equation with this substitution. c) What property of equality should she use to solve the equation for 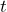 ? Rewrite the equation after using this property of equality. d) What property of equality should she use to rearrange the solved equation to the form
? Rewrite the equation after using this property of equality. d) What property of equality should she use to rearrange the solved equation to the form 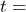 a number? e) What is the maximum price of tv Hayley can afford to buy?
a number? e) What is the maximum price of tv Hayley can afford to buy?
Show/Hide Answer
- Yes, he is correct. The subtraction property of equality allows us to subtract the same number from both sides of an equation to write an equivalent equation.
- a) 30 is multiplied onto
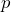 so to get rid of the 30, we need to divide both sides of the equation by 30. This will get
so to get rid of the 30, we need to divide both sides of the equation by 30. This will get 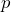 on its own since the 30s will cancel to 1 on the left side of the equation. b) The division property. c) Dividing both sides of an equation is equivalent to dividing the same amount on both sides by the same value. So an equivalent equation will be formed that does not affect the value of the variable.
on its own since the 30s will cancel to 1 on the left side of the equation. b) The division property. c) Dividing both sides of an equation is equivalent to dividing the same amount on both sides by the same value. So an equivalent equation will be formed that does not affect the value of the variable. - a) Yes; Total cost = tv price + tax, so
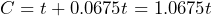 b)
b) 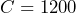
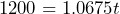 c) Division property of equality.
c) Division property of equality. 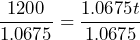 which simplifies to
which simplifies to 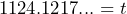 d) Symmetric property:
d) Symmetric property: 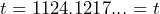 e) $1124.12
e) $1124.12
 In this section, we will take what we have learned and apply the concepts to new situations.
In this section, we will take what we have learned and apply the concepts to new situations.
Perspectives
- Gary is buying an engagement ring for his girlfriend. The ring they have chosen costs $12,500. Gary has saved $3600 towards the ring. a) Define a variable and write an equation that could be solved to find the amount Gary will need to finance. b) What property of equality should be used to solve the equation? c) Solve the equation to determine the amount Gary will finance.
- Pierre rents a bicycle when he is on holiday in Amsterdam. The cost was 8 euros per day. If Pierre paid 104 euros for the rental, define a variable and set up an equation that could be solved to determine the number of days Pierre rented the bicycle. b) What property of equality should be used to solve the equation? c) Solve the equation to determine the number of days Pierre rented the bicycle.
- Debra is selling a pair of designer shoes on an online store, Posh Stuff. The site charges a standard fee of 5% of the item’s selling price. Debra bought the shoes on sale for $220, and wore them once. They retail for $380. Debra would like to make $100 in profit from the sale. a) Define a variable and write an equation to determine the selling price on Posh Stuff. b) Use the equation to determine the selling price to the nearest ten dollars.
- The Red Cross claims that “on average, 90 cents of every dollar we spend is invested in delivering care and comfort to those in need.”[1] a) Define a variable and write an equation that could be solved to find the amount that is donated if $8.2 million was invested in delivering care and comfort to those in need. b) Solve the equation to determine the amount donated. Round your answer to the nearest hundred thousand dollars.
Show/Hide Answer
- a) Let
 = the amount Gary will finance, then
= the amount Gary will finance, then 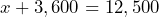 b) subtraction property: subtract 3,600 from both sides c) $8900
b) subtraction property: subtract 3,600 from both sides c) $8900 - a) Let
 = the number of days, then
= the number of days, then 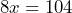 b) division property: divide both sides by 8 c) 13 days
b) division property: divide both sides by 8 c) 13 days - a) Let
 = the selling price, then
= the selling price, then 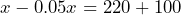 b) $340
b) $340 - a) Let
 = the amount donated, then
= the amount donated, then 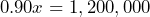 b) $1.3 million
b) $1.3 million
 In this section, we will use what we have learned so far to practice skill problems.
In this section, we will use what we have learned so far to practice skill problems.
Skill Exercises
Solve the equation:
Show/Hide Answer
two or more equations that look different but have the same solution
if a = b, then b = a

