5-4: Solving Linear Equations in One Variable

Hazel McKenna; Leo Chang; Roxanne Brinkerhoff

CHAPTER 5: LINEAR EQUATIONS IN ONE VARIABLE

5-4: Solving Linear Equations in One Variable

Introduction

Being able to solve linear equations in one variable is necessary to support learning of other topics in mathematics. It is also necessary to be able to transfer the skill of equation solving to other subject areas. But this can only happen if we understand the conceptual knowledge surrounding solving linear equations and don’t rely on procedural knowledge. In other words, knowing the steps required to solve linear equations is not going to get us very far. Understanding what a linear equation is telling us is the key to solving linear equations and being able to transfer our knowledge to other fields of inquiry.

Solving Linear Equations in One Variable

To solve an equation is to determine the value of the variable that will satisfy or make the conditional equation true. To satisfy or make an equation true means the left side and the right side of an equation will be equal once we substitute the variable with the correct value (i.e., the solution). For example, in the equation $x+3=5$ , the value of $x$ cannot be 4 because 4+3 is not equal to 5. Indeed, $x=2$ is the only value that makes the equation true, so $x=2$ is the solution of the equation.

A linear equation in one variable has only one variable whose exponent is 1 (e.g., $x$ ). Such equations often come from simplifying linear equations with more than one variable by substituting specific values for all but the one variable we are interested in. For example, knowing that $C=20$ in the equation $C=(F-32)\div1.8$ simplifies the linear equation in two variables (i.e., $C$ and $F$ ) to $20=(F-32)\div1.8$ . This results in a linear equation in one variable that can be solved for the only variable $F$ .

To solve a linear equation in one variable, we use the properties of equality to isolate the variable on one side of the equation. That is, to end up with an equation of the form variable = number.

Explore 1 – Solving a linear equation

Calum owns a 1973 Mini Cooper. He needs to buy a new clutch for the car but only has $250 to spend. Tax on his purchase is 6.5%. What is the maximum price he can pay for the new clutch?

Solution

Before we write an equation we need to think about what makes up that equation. We need to understand the equation by asking questions: What do we know and what do we need to find? How are the known and unknown related?

Known: total cost = $250; tax rate = 6.5% Unknown: price of the clutch; tax paid on the price of the clutch Relationship: The total cost of the clutch = price + tax

So, if we define $p=$ price, then tax = 6.5% of $p$ and the equation $250=p+0.065p$ can be used to determine the price $p$ . (Remember: tax = tax rate $\times$ price)

$250=p+0.065p$ is a linear equation in one variable (i.e., $p$ ).

Before we get into solving for $p$ , we can simplify the right side of the equation by adding like terms: $250=1.065p$ Always simplify as much as possible before applying the properties of equality: $1p+0.065p=(1+0.065)p=1.065p$

To solve for $p$ means we have to get $p$ on its own on one side of the equation. This is called isolating the variable.

Notice that in the equation $250=1.065p$ , $p$ is multiplied by 1.065. To isolate the variable $p$ we must undo the multiplication by dividing by 1.065. We use the division property of equality and divide both sides of the equation by 1.065: $\dfrac{250}{1.065}=\dfrac{\cancel{1.065}p}{\cancel{1.065}}$ This allows us to cancel 1.065/1.065 = 1 and simplify $1p=p$ .

After canceling the right side of the equation, the equation simplifies to: $234.7417...=p$

The property of symmetry then allows us to switch sides so that $p=234.7417...$

Finally, we get to answer the question. Since we defined $p$ , we need to go back to English to answer the question, and since we are working with money, we will round to the nearest cent.

The maximum price Calum can afford for the clutch is $234.74.

Solving the equation is written mathematically as:

$\begin{aligned}250&=p+0.065p\\250&=1.065p\\\dfrac{250}{1.065}&=\dfrac{\cancel{1.065}p}{\cancel{1.065}}\\234.7417...&=p\end{aligned}$

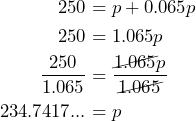
Any time a variable term has a number (coefficient) multiplied onto it, we must undo the multiplication by dividing by that number to isolate the variable (i.e., get the variable on its own).

Most linear equations cannot be solved by using only one property of equality. Most will require two or more properties of equality to be used to isolate the variable.

Explore 2 – Solving a linear equation

Dasan bought two pairs of shoes for his twins. He noticed that shipping cost $5.99 and the total cost was $93.49. Write an equation that represents this situation then solve the equation to determine the price of each pair of shoes.

Solution

Before we write an equation we need to think about what makes up that equation. We need to understand the equation by asking questions: What do we know and what do we need to find? How are the known and unknown related?

Known: shipping = $5.99; total cost = for $93.49; number of pairs of shoes bought = 2. Unknown: price of a pair of shoes

Relationship: (number of pairs of shoes) times (price of a pair of shoes) + shipping = total cost

To write the equation, we must define a variable to represent the price of a pair of shoes. So, we define $s$ =price of a pair of shoes. Then, $2s+5.99=93.49$

To solve the equation $2s + 5.99 = 93.49$ we first want to isolate the variable term (i.e., $2s$ ). The variable term has 5.99 added to it. To isolate the variable term we must undo that addition by subtracting 5.99 from both sides of the equation using the subtraction property of equality: $2s+5.99\color{blue}-5.99 \color{black}= 93.49\color{blue}-5.99$

This simplifies to the equivalent equation: $2s=87.5$

Now that we have the variable term isolated, we can isolate the variable $s$ . The variable $s$ is multiplied by 2, so we must undo the multiplication by dividing by 2. This means that we use the division property of equality to cancel the 2 to 1.

Divide both sides of the equation by 2: $\dfrac{\cancel{2}s}{\color{blue}\cancel{2}}\color{black}=\dfrac{87.5}{\color{blue}2}$

This simplifies to the equivalent equation: $s=43.75$

We have solved the equation for $s$ and since $s$ was defined as the price of one pair of shoes, we can answer the question.

The price of each pair of shoes was $43.75.

Solving the equation is written mathematically as:

$\begin{aligned}2s+5.99 &= 93.49 \\ 2s+5.99\color{blue}-5.99 \color{black}&= 93.49\color{blue}-5.99\color{black} \;\;\; \text{(subtraction property of equality)} \\2s&=87.5 \\ \frac{2s}{\color{blue}2\color{black}} &= \frac{87.5}{\color{blue}2\color{black}} \;\;\; \text{(division property of equality)} \\ s&=43.75\end{aligned}$

Applying the properties of equality results in equivalent equations that have the same solution as the original equation. These equations get simpler the closer we get to a solution. When we have a number added to a variable term, we use the subtraction property of equality to isolate the variable term. Once the variable term is isolated, we can solve for the variable by applying the division property of equality.

Explore 3 – Solving a linear equation

Uber charges a base fee of $10 per ride, then charges $1.50 per mile for each mile traveled. Jose would like to limit how much he spends on Uber to $35, how many miles can he travel?

Solution

We need to write an equation that we can solve to determine the number of miles Jose can travel.

We start by defining a variable to represent the unknown number of miles: Let $x=$ the number of miles traveled.

We know the total charge is $35, the base fee is $10, and the mileage charge is $1.50 $\times$ (the number of miles traveled).

The equation is: total charge = base fee + mileage charge

So: $35=10+1.50x$

To solve this equation we will first isolate the variable term, then isolate the variable:

$\begin{aligned}1.5x+10 &= 35 \\ 1.5x+10\color{blue}-10\color{black} &= 35\color{blue}-10 \color{black}\;\;\; \text{(subtraction property of equality)} \\1.5x&=25 \\ \frac{1.5x}{\color{blue}1.5\color{black}} &= \frac{25}{\color{blue}1.5\color{black}} \;\;\; \text{(division property of equality)} \\ x&=16.66\overline{6}\end{aligned}$

Finally, we answer the question: Jose can travel 16.67 miles for $35.

It is often useful to write the equation in English before jumping in with numbers and variables. This makes us stop to think about how the equation is put together, and by doing this we are less likely to make an error. After we have solved the equation, there are a couple of things we can do to make sure the solution is correct. First, we can check that the equation has been solved correctly by substituting our answer back into the equation to make sure it is a solution. For example, in Explore 3, if we substitute $x=16.67$ into the original equation $1.5x+10=35$ , the equation becomes $1.5(16.67)+10=35$ , which simplifies to $35.005 \approx 35$ . Given that we rounded our answer $x=16.66\overline{6}$ to 16.67, the result $35.005 \approx 35$ is good enough to be equal. So now we know we solved the equation correctly. The second thing we need to consider is whether or not our equation was correct to start with. We can do this by checking the critical thinking we used to write the equation (i.e., total charge = base fee + mileage charge) and by considering whether or not the answer we got is reasonable. In other words, does the answer make sense? In this case, does it seem reasonable that an Uber ride of 16.67 miles would cost $35? We have to use common sense and lived experience to make such judgements. Of course, it’s always easier to catch an obviously unreasonable answer. For example, if our decimal point was in the wrong place and we got an answer of either 1.667 miles or 166.7 miles we’d realize that both are off for a charge of $35!

Explore 4 – Variable terms on both sides

A bake sale committee would like to determine how many cupcakes they need to sell in order to break even. The location for their bake sale will cost $200. Every dozen cupcakes costs $8 to make. Every cupcake will be sold for $1.50. How many cupcakes will the committee need to sell in order to break even?

Solution

To break even means that the amount they spend to make and sell the cupcakes (the cost) equals the amount of money they will bring in from selling the cupcakes (the revenue). In other words, they will neither make a profit nor a loss.

Their cost consists of $200 for the location and $8 for every dozen cupcakes. Their revenue consists of $1.50 for each cupcake they sell.

If 12 cupcakes costs $8 to make, then each cupcake costs $8/12 = $0.67.

The unknown quantity is the number of cupcakes that need to be sold, so we define $x=$ number of cupcakes sold.

At the break even point, cost = revenue, with cost = $200 for the location + $0.67 times the number of cupcakes sold, and revenue = $1.50 times the number of cupcakes sold.

The equation is then $200+0.67x=1.5x$

Notice that there are $x$ -terms on both sides of the equation. So our first goal is to get all the variable terms on the same side of the equation by subtracting $0.67x$ from both sides using the subtraction property of equality: $200+0.67x\color{blue}-0.67x\color{black}=1.5x\color{blue}-0.67x$

Simplifying results in the equivalent equation: $200=0.83x$

Now that the variable term is isolated, we can isolate the variable $x$ using the division property of equality. $x$ is multiplied by 0.83 so we divide both sides by 0.83: $200\color{blue}\div0.83\color{black}=0.83x\color{blue}\div0.83$ which simplifies to $240.96=x$

Now that we have solved the equation, we can answer the question: They will have to sell 241 cupcakes to break even.

To write this mathematically, each equation is equivalent to the one above it:

$\begin{aligned}200+0.67x &= 1.5x \\ 200+0.67x\color{blue}-0.67x\color{black}&=1.5x\color{blue}-0.67x \color{black}\;\;\; \text{(subtraction property of equality)} \\ 200&=0.83x\;\;\;\text{(simplify by subtracting like terms)}\\200\color{blue}\div0.83\color{black}&=0.83x\color{blue}\div0.83\color{black}\;\;\;\text{(division property of equality)}\\240.96&=x\end{aligned}$

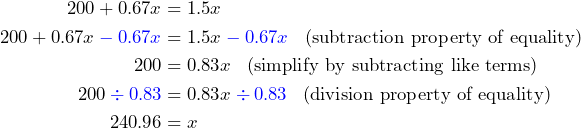
To check this for reasonability we can think of 240 cupcakes as 20 dozen cupcakes (20 · 12 = 240). And the cost of baking 20 dozen is $8 · 20 = $160. That added to the location cost of $200 = $360. On the other hand, their revenue is $1.50 per cupcake which amounts to $1.50(240) – $360. So our answer appears to make sense.

When we solve equations it is customary to write each equivalent equation directly below the equation we manipulate, with the = signs lined up. This makes it much easier to see what is happening, and to catch any errors that may occur.

Explore 5 – Variable terms on both sides

At a baseball game, Enola goes to the concession stand and buys 3 hot dogs and a $6 soda. Her friend, Malia also goes to the concession stand and buys 4 hot dogs. They are comparing the receipts and find that they both spent the same amount on their purchases. Determine the price of a hot dog.

Solution

First we define a variable to represent the unknown: Let $x=$ price of a hot dog

Enola’s receipt: $3x+6$

Malia’s receipt: $4x$

Since the receipts total the same amount, we can set them equal then solve for $x$ :

$\begin{aligned}3x+6&=4x\\3x\color{blue}-3x\color{black}+6&=4x\color{blue}-3x\color{black}\;\;\;\text{(subtraction property of equality)}\\6&=x\end{aligned}$

The hot dogs cost $6 each.

Since concessions are notoriously overpriced at ball games, a $6 hot dog seems reasonable.

Solving a linear equation in one variable

Simplify each side of the equation, if required. Use the distributive property to eliminate parentheses, and combine like terms.
Isolate the variable term on one side of the equation and numbers on the other side. Use the addition or subtraction property of equality.
Isolate the variable. Use the multiplication or division property of equality.
Check your answer in the original equation to make sure it is a solution.
Check your answer for reasonability using common sense and lived experience.

Reflect Icon

What is the purpose of solving an equation?

Show/Hide Answer

The purpose of solving an equation is to determine the value of the variable that will satisfy the equation or make the equation true.

What is a solution of an equation?

Show/Hide Answer

The solution of an equation is a number that will satisfy the equation or make the equation true if the value of the variable is substituted into the equation.

Exactly how many solutions does a conditional linear equation in one variable have?

Show/Hide Answer

One.

How would we undo subtraction in an equation?

Show/Hide Answer

To undo subtraction, we add the same amount to both sides of the equation.

How would we undo multiplication in an equation?

Show/Hide Answer

To undo multiplication, we divide both sides of the equation by the same amount.

Practice Exercises

Forensic scientists use the equation 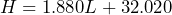$H=1.880L+32.020$ to estimate the height in inches of an adult male whose skeletal remains include a femur bone of length 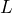$L$ inches. A lab technician measures a femur bone at 16.5 inches. Determine the approximate height of the man the femur bone belonged to.
The equation 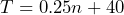$T=0.25n+40$ represents the ambient air temperature ( 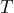$T$ related to the number of chirps per minutes ( 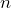$n$ ) of a cricket. a) If a cricket chirps 100 times per minute, use the equation to determine the ambient air temperature. b) If the ambient air temperature is 46°F, how many chirps per minute can you expect from the crickets?
The 2021 Census counted 1.8 million Indigenous people, accounting for 5.0% of the total population in Canada^[1]. Write an equation then use it to determine the population of Canada.

Show/Hide Answer

63.04 inches = 5 ft 3 in
a) 65°F b) 24 chirps per minute
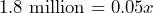$1.8 \text{ million} =0.05x$ Population of Canada is 36 million.

In this section, we will take what we have learned and apply the concepts to new situations.

Perspectives

In 2021, there were 70,545 Inuit living in Canada, with 69.0% living in Inuit Nunangat—the homeland of Inuit in Canada. Write an equation and use it to determine how many Inuit live in Inuit Nunangat.
A popular donut shop spends $0.13 per donut to produce their award-winning donuts. In addition, they pay $1350 in utilities and $5300 in salaries and benefits per month. a) Defining 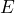$E$ as the total monthly expenses and 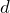$d$ as the number of donuts produced, write an equation that relates 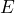$E$ in terms of 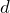$d$ . b) The store manager calculated the total expenses for March as $13,150. Use the equation to determine many donuts were produced in March? c) The shop sells each donut for $0.75. What was the shop’s revenue in March? d) How much profit did the store make in March? e) Write an equation that could be used to calculate the monthly break even point. f) Calculate the monthly break even point g) Write an equation that relates the monthly profit to the number of donuts sold. Define 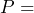$P=$ monthly profit. h) If the store manager plans to make a profit of $30,000 in April, how many donuts will the shop have to sell?
Working as an insurance salesman, Brian makes a base wage of $35,000 plus a commission of $80 on every policy he sells. a) If 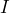$I$ represents his yearly income and 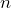$n$ represents the number of policies he sells in a year, write an equation that relates his income in terms of the number of policies he sells. b) Use the equation to determine Brian’s income if he sells 160 policies. c) Use the equation to determine how many policies Brian needs to sell to have an income of $60,000.
The number of American military fatalities from WWI (1917-18) and WWII (1939-45) combined was less than those of the American Civil War (1861-65). 288,883 more military personnel were killed in WWII than WWI. The American Civil War accounted for 98,085 more military fatalities than WWI and WWII combined. If there were an estimated 620,000 military fatalities in the American Civil War, how many military fatalities were there in WWI and WWII?
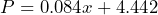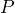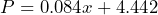Between 1980 and 2021 the world population increased from 4.442 billion to 7.888 billion almost linearly^[2]. The equation $P=0.084x+4.442$ approximates the population $P$ in billions between 1980 and 2021, $x$ years after 1980. a) In which year did the population reach 6 billion? b) In which year did the population reach 7 billion? c) How do the solutions from the model $P=0.084x+4.442$ compare to the actual world population data? If there are differences, how would you account for those differences?
If 75 gallons of water are added to a pool that is already half full, the pool becomes two-thirds full. a) Define a variable and write an equation to determine the capacity of the pool. b) Use the equation to determine the capacity of the pool.
On the same day that Calum bought a $40,000 car, Kirsty bought a plot of land for $6000. Calum’s car is expected to lose $1450 per year, while Kirsty’s land is expected to gain $550 per year. a) Define a variable and write an equation to determine when the value of Calum’s car will equal that of Kirsty’s land. b) Use the equation to determine when the two values will be the same.
In a survey on civics, Americans were asked the question, “How many branches does the U.S. government have?” The number of people who answered correctly, 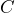$C$ , can be determined using the equation 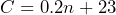$C = 0.2n + 23$ , where 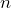$n$ represents the total number of people who took the test. a) If 120 Americans took the survey, how many of them answered the question correctly? b) Suppose 200 Americans answered the question correctly, how many of them took the test?

Show/Hide Answer

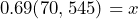$0.69(70,545)=x$ 48,767 Inuit live in Inuit Nunangat.
a) 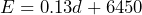$E=0.13d+6450$ b) 51,538 c) $38,653.50 d) $25,503.50 e) 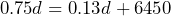$0.75d=0.13d+6450$ f) 10,403 donuts sold g) 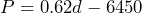$P=0.62d-6450$ h) 37,984 donuts
a) 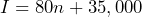$I=80n+35,000$ b) $47,800 c) 313 policies
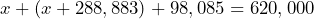Let $x$ = number of military fatalities in WWI. Equation: $x + (x + 288,883) + 98,085 = 620,000$ WWI = 116,516 WWII = 405,399
a) 1998 b) 2010 c) They are very close; just off my a few months. The differences can be accounted for by rounding in the model.
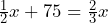a) Let $x$ = the capacity of the pool, then $\frac{1}{2}x+75=\frac{2}{3}x$ b) 450 gallons
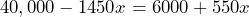a) Let $x$ = the number of years, then $40,000-1450x=6000+550x$ b) 17 years
a) Only 47 of the 120 answered the questions correctly. b) 885 Americans had to take the survey to get 200 correct answers.

Skills Icon In this section, we will use what we have learned so far to practice skill problems.

Skill Exercises

Solve the equation:

$x+4=9$
$x-8=-2$
$3x=-9$
$\frac{1}{2}x=5$
$3x+4=10$
$2x-7=11$
$\frac{1}{3}x-1=2$
$2(x+4)=-12$
$-3x+8=9$
$-3(x+4)=2x$
$2x+5=9x-2$
$5x-3(2x+1)=9$
$\frac{3}{4}x-4=\frac{1}{4}x+3$
$-2(x-5)+4=9(x-4)+6$
$0.2x+7.3=0.5x$

Show/Hide Answer

$x=5$
$x=6$
$x=-3$
$x=10$
$x=2$
$x=9$
$x=9$
$x=-10$
$x=-\frac{1}{3}$
$x=-\frac{12}{5}$
$x=1$
$x=-12$
$x=14$
$x=4$
$x=2.19$

https://www150.statcan.gc.ca/n1/daily-quotidien/220921/dq220921a-eng.htm ↵
https://datacommons.org/place/Earth?utm_medium=explore&mprop=count&popt=Person&hl=en ↵

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License