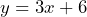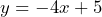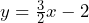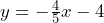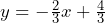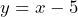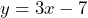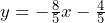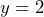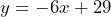CHAPTER 6: LINEAR GROWTH
6-5: Solving Linear Equations in Two Variables
Introduction
In addition to modeling and translating a linear pattern into a linear equation, we can go on to use the linear equation to solve problems. As long as the linear pattern continues we can solve the equation for specific values of either the dependent variable or the independent variable.
 Solving a Linear Equation for an Independent Value
Solving a Linear Equation for an Independent Value
Explore 1 – Determining an independent value
There is a fiber infrastructure construction project along a road. The project completes 20 meters along the road every day. So far 200 meters have been completed from the starting point.
- Define the independent and dependent variables, and write the units of each variable.
Solution
Let ![]() = the number of days and
= the number of days and ![]() = the number of meters completed.
= the number of meters completed.
- Write an equation to represent the linear progress of the construction project.
Solution
The initial value is 200m and the rate of change is 20 meters per day, so ![]()
- How many more days will it take for the project to reach your house if your house is 800 meters from the starting point?
Solution
Since the unit of the variable ![]() is meters, we substitute 800 for
is meters, we substitute 800 for ![]() and then solve for
and then solve for ![]() :
:
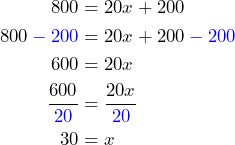 .
.
It will take 30 days more for the project to reach your house.
- Suppose the road is 1500 meters long. How many more days will it take to complete the project?
Solution
Since the unit of the variable ![]() is meters, we substitute 1500 for
is meters, we substitute 1500 for ![]() and then solve for
and then solve for ![]() :
:
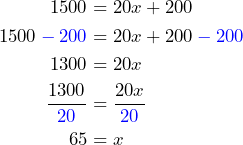
It will take 65 days more for the project to be completed.
Explore 2 – Determining an independent value
Automated speed cameras are becoming more and more common on interstates throughout the U.S. The way that these automated cameras work is that they record your license plate number and the time that you pass a camera. With this information, your average speed between cameras can be calculated and speeding tickets can be issued based on these calculations.
- Suppose that Evan goes through the first speed camera at 8:00 and at 8:30 he arrives at the second speed camera, which is 45 miles away. What is Evan’s average speed (rate) between the two cameras?
Solution
The independent variable is time in minutes and the dependent variable is distance in miles.
The rate is ![]() 1.5 miles per minute
1.5 miles per minute
To convert this to miles per hour we use the fact that 1 hour = 60 minutes:
![]()
Therefore, Evan’s average speed is 90 mph.
- If the speed limit of the highway is 70 mph will Evan be given a speeding ticket?
Solution
Yes, Evan averaged 20 mph over the speed limit so he will be given a speeding ticket.
- Define the variables and write an equation to model the distance traveled at a speed of 70 miles per hour.
Solution
Let ![]() = time in hours and
= time in hours and ![]() = distance traveled in miles.
= distance traveled in miles.
The initial value is 0 miles since if no time has elapsed no distance has been traveled, and the rate is 70 miles per hour:
![]()
- What time will Evan get to the second speed camera if he drives at an average speed of 70 mph?
Solution
Since we are looking for time, we will be solving the equation for ![]() . The unit of the variable
. The unit of the variable ![]() is miles, so we substitute 45 for
is miles, so we substitute 45 for ![]() and solve for
and solve for ![]() :
:
 .
.
It will take 0.64 hours to reach the second camera.
We can change hours into minutes using the fact that 1 hour = 60 minutes:
![]() .
.
Therefore, it takes Evan 38.4 minutes to reach the second camera. The time will be at 8:38.
Example
- Jane plants a timber bamboo[1] plant that is 3 inches tall. She measures the height of the plant daily:
| Time (days) | 0 | 1 | 2 | 3 | 4 | 5 |
| Height (in) | 3 | 5 | 7 | 9 | 11 | 13 |
a) Define the independent and dependent variables along with their units.
b) Determine the initial value and rate of change.
c) Write an equation that represents the height of the plant over time.
d) How long will it take the plant to grow to 3 feet?
e) How long will it take the plant to grow to 150 feet?
f) Will the pattern of growth stay linear forever? State your reasoning.
Show/Hide Answer
- a) Let
 = times in days and
= times in days and  = height in inches b) initial value = 3 inches. Rate of change = 2 inches per day. c)
= height in inches b) initial value = 3 inches. Rate of change = 2 inches per day. c) 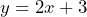 d) 3 feet = 36 inches:
d) 3 feet = 36 inches: 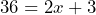 so it will take 33/2 days = 16.5 days. e) 150 feet = 1800 inches:
so it will take 33/2 days = 16.5 days. e) 150 feet = 1800 inches: 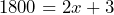 so it will take 898.5 days = 2 years 168.5 days. f) No. Plant growth declines as the plants gets older.
so it will take 898.5 days = 2 years 168.5 days. f) No. Plant growth declines as the plants gets older.

- How do you determine whether a number you are given is an independent value or a dependent value? In other words, how do you know whether you need to substitute the number for
 or for
or for  in a linear equation?
in a linear equation?
Show/Hide Answer
The substitution is based on the units of the number we are given. If the units match the units of the independent variable we substitute the number for ![]() , and if the units match the units of the dependent variable we substitute the number for
, and if the units match the units of the dependent variable we substitute the number for ![]() .
.
 Using Linear Reasoning to Determine an Initial Value
Using Linear Reasoning to Determine an Initial Value
It is not uncommon to have to solve a problem where the initial value is not given. Rather we are given other data values and we can use linear reasoning to determine the initial value and write an equation to represent the situation.
Explore 3 – Find the initial value using linear reasoning
Jake is having a potluck party at a friend’s house. It’s 5pm. It has been snowing the whole day. The snow accumulates at a rate of 2 inches per hour.
1. Define the independent and dependent variables along with their units.
Solution
Independent Variable: ![]() Time in hours
Time in hours
Dependent Variable: ![]() Depth of snow in inches
Depth of snow in inches
2. At 10 pm, the depth of snow is 18 inches. What is the depth of snow at 5pm?
Solution
Since the snow accumulates in a linear rate, the depth of snow may be represented by the equation ![]() where b is the initial depth of snow at 5pm. Since the depth of snow is 18 inches after 5 hours starting at 5pm, the equation
where b is the initial depth of snow at 5pm. Since the depth of snow is 18 inches after 5 hours starting at 5pm, the equation ![]() becomes
becomes ![]() or
or ![]() . Therefore,
. Therefore, ![]() .
.
The depth of snow is 8 inches at 5pm.
3. Use linear reasoning to determine if Jake would have difficulty driving home at 2:00 am?
Solution
At 5pm, the depth of snow is already 8 inches. Since the snow accumulates at the rate of 2 inches per hour, the depth of snow will be ![]() inches, which is 2 feet and 2 inches. This means Jake might have difficulty driving home if the road was not plowed.
inches, which is 2 feet and 2 inches. This means Jake might have difficulty driving home if the road was not plowed.
4. Write an equation to represent the linear relation between time and the depth of snow.
Solution
The initial value at 5pm is 8 inches, and the snow cumulation rate is 2 inches per hour. Therefore, the equation is ![]()
5. Use the equation to determine how long it would take for the snow to accumulate to 5 feet.
First, we will convert 5 feet to 60 inches (![]() ) because the unit used in the equation is in inch.
) because the unit used in the equation is in inch.
If the depth of snow = 60 inches, then ![]() :
: ![]()
Solving for ![]() :
: ![]()
So, ![]()
After 26 hours (one day and two hours), the depth of snow will be 5 feet.
Explore 4 – Find the initial value using a linear equation
Emily is a college student in Utah. She saved a certain amount of money and spent her summer in Seattle using the money she saved. When living in Seattle, Emily spent $450 each week on rent, food, and activities. She still has $2,000 left after 8 weeks of living in Seattle.
- Define the independent and dependent variables along with their units.
Solution
The independent variable is ![]() = time in weeks and the dependent variable is
= time in weeks and the dependent variable is ![]() = money left from savings in dollars.
= money left from savings in dollars.
- Determine the rate of change of Emily’s savings.
Solution
Rate of change = –$450 per week.
- Write an equation to represent the linear relation between the amount of money remaining and the rate of spending money. Use
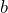 to represent the initial value of the money Emily saved.
to represent the initial value of the money Emily saved.
Solution
![]()
- How much money did Emily save?
Solution
Emily saved a total of ![]() , the initial value. We need to determine the value of
, the initial value. We need to determine the value of ![]() .
.
We know that ![]() and that an
and that an ![]() data point is (8, 2000). Therefore, we can use the equation and substitute
data point is (8, 2000). Therefore, we can use the equation and substitute ![]() and
and ![]() to determine the value of
to determine the value of ![]() :
:
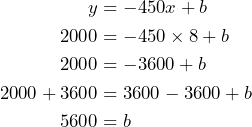
Therefore, Emily saved $5600.
- How long will Emily be able to live in Seattle before she runs out of money?
Solution
Since ![]() . the linear equation is
. the linear equation is ![]() .
.
Emily runs out of money when ![]() :
:
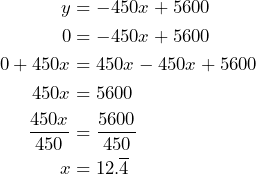
Emily will run out of money after 12 weeks.

- What information do you need to determine the initial value given a linear equation with the initial value unknown?
Show/Hide Answer
We need to know the rate of change and a pair of data values; an independent value and the corresponding dependent value. Then we substitute the two values into the equation, and solve for the unknown initial value.
Practice Exercises
- The price of a movie ticket is $8.50. a) Define variables to represent the independent and dependent variables along with their units. b) Write an equation that represents the cost of buying some quantity of movie tickets. c) How much will it cost to buy 12 tickets? d) If James has $50, how many tickets can he buy?
- Erin and Rachel bought a house together in 2016 for $365,000. In 2021, the house was valued at $520,000. Assuming a constant price increase per year, calculate the cost of the house when it was first built in 2012.
- Chris works at an aquarium and needs to clean a 175 gallon reef tank. After carefully removing the fish, Chris Chris must use a siphon to drain the tank. The siphon drains the tank at 6.25 gallons every 15 minutes. a) Calculate the drainage rate per hour. b) Define the variables and write an equation that represents the amount of water in the tank based on the time the siphon has been running. c) How much water is in the tank after 1.5 hours? d) How long will it take to drain the tank?
Show/Hide Answer
- Let
 = number of tickets (a whole number) and
= number of tickets (a whole number) and  = total cost in dollars. b)
= total cost in dollars. b) 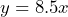 c) $102 d) 5 tickets
c) $102 d) 5 tickets - $241,000
- a) 25 gallons per hour b) Let
 = time in hours and
= time in hours and  = amount of water in the tank in gallons, then
= amount of water in the tank in gallons, then 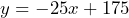 c) 137.5 gallons d) 7 hours
c) 137.5 gallons d) 7 hours
 In this section, we will take what we have learned and apply the concepts to new situations.
In this section, we will take what we have learned and apply the concepts to new situations.
Perspectives
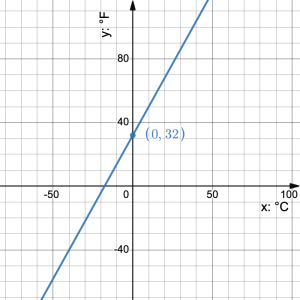 The graph represents the relationship between temperatures
The graph represents the relationship between temperatures  in degrees Fahrenheit and
in degrees Fahrenheit and  in degrees Celsius. a) What is the
in degrees Celsius. a) What is the  -intercept? b) At what point does °C = °F? c) Determine the slope of the line. d) Write an equation that represents the relationship between temperatures in degrees Fahrenheit and degrees Celsius. e) If it is –5°C outside, what is the temperature in degrees Fahrenheit? f) If an oven temperature is 375°F, what is the same temperature in Celsius?
-intercept? b) At what point does °C = °F? c) Determine the slope of the line. d) Write an equation that represents the relationship between temperatures in degrees Fahrenheit and degrees Celsius. e) If it is –5°C outside, what is the temperature in degrees Fahrenheit? f) If an oven temperature is 375°F, what is the same temperature in Celsius?- A truck rental agency charges a fixed daily rate to hire a truck plus a set fee of $30 for insurance coverage. Betsy hired a truck for 4 days for a total cost of $420. When she hired a truck for 7 days the total cost was $712.50. a) Calculate the fixed daily rate to hire a truck. b) Define the variables and write an equation that represents the total cost of hiring a truck for any number of days. c) What would be the cost to hire a truck for 14 days? d) Betsy’s friend Dan has a budget of $1500 to rent a truck for his company for as long as possible. How many days can Dan rent the truck?
- A small company sells handmade surfboards. They incur a fixed monthly cost of $8500 for rent, utilities, insurance, and other expenses. It costs $1750 in time and materials to build a surfboard. a) Define the variables and write an equation that represents the total cost of building a number of surfboards. b) If they sell the surfboards for $3500, write an equation that would represent the revenue they would receive from selling a number of surfboards. c) Write an equation that represents the profit they would make from selling a number of surfboards. d) Determine how many surfboards they would have to make and sell to make a profit of $20,000 per month.
- At the start of 2020, the World’s proven oil reserves 1,779,685 million barrels, and were produced at a rate of 29,427 million barrels per year.[2] Assume the rate of production stays constant. a) Define the variables and write an equation that represents the World’s oil reserves in terms of the number of years since 2020. b) Use the equation to determine the World’s oil reserves in 2030. c) Determine the number of years of oil production left to diminish the World’s oil reserves to zero. d) INVESTIGATE: What would save the World’s oil reserves from extinction?
- A band is performing at a club for a fee of $1500 plus 20% of all ticket sales. A ticket for the concert is $55. The maximum capacity of the club is 900 people. a) Define the variables and write an equation that represents the total owed to the band. b) What is the minimum fee the band will receive? c) What is the maximum fee the band will receive? d) If the band wants to make at least $5000 for the gig, how many tickets will need to be sold?
- A coffee roaster offers a club membership for $45 to join and $75 per month. Each month the members receive a package of their favorite freshly roasted coffee along with a sample of a different roast. a) Define the variables and write an equation that represents the total cost of belonging to the club for a number of months. b) How much would it cost to be in the club for one year? c) Millard calculates that he has spent about $3000 with the club. Determine how long he has been with the club.
- Bert bought a new car in 2016. In 2018, it was valued at $22,500. The same car was valued at $14,500 in 2022. a) Assuming a constant drop in the value of the car each year, define the independent and dependent variables along with their units. b) Calculate the rate of depreciation regarding the car’s value. c) Use linear reasoning to calculate the value of the car in 2016 when it was new. d) Write an equation to represent the linear relation between the car’s value and year. e) When will the car’s value drop to $5000?
Show/Hide Answer
- a) (0, 32) b) (–40, –40) c) 9/5 d)
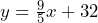 e) –5°C = 23°F f) 375°F = 190.6°C
e) –5°C = 23°F f) 375°F = 190.6°C - a) $97.50 b) Let
 = number of days and
= number of days and  = the total cost in dollars, the
= the total cost in dollars, the 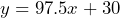 c) $1395 d) 15 days
c) $1395 d) 15 days - a) Let
 = number of surfboards and
= number of surfboards and  = the total cost in dollars, then
= the total cost in dollars, then 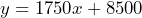 b) Let
b) Let  = number of surfboards and
= number of surfboards and 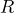 = the total revenue in dollars, then
= the total revenue in dollars, then 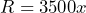 c) Let
c) Let  = number of surfboards and
= number of surfboards and 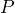 = the profit in dollars, the
= the profit in dollars, the 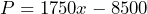 d) 17
d) 17 - a) Let
 the number of years since 2020, and
the number of years since 2020, and  = the World’s oil reserves in millions of barrels, then
= the World’s oil reserves in millions of barrels, then 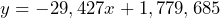 b) 1,485,415 million barrels c) 60.5 years
b) 1,485,415 million barrels c) 60.5 years - a) Let
 = number of tickets sold and
= number of tickets sold and  = total fee, then
= total fee, then 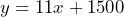 b) $1500 c) $11,400 d) at least 319 tickets
b) $1500 c) $11,400 d) at least 319 tickets - a) Let
 = number of months and
= number of months and  = total cost, then
= total cost, then 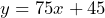 b) $945 c) about 39 months or 3 years 3 months
b) $945 c) about 39 months or 3 years 3 months - a) The independent variable is
 = time in years and the dependent variable is
= time in years and the dependent variable is  = value in dollars. b) Rate of change =
= value in dollars. b) Rate of change = 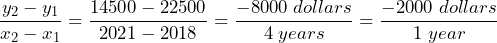 . The car’s value depreciates at $2000 per year. c) We can use linear reasoning knowing that 2016 is 2 years prior to 2018 when the car was valued at $14,500. Since the rate of depreciation is $2000 per year it must have been worth 2($2000) = $4000 more in 2016 than in 2018. So the initial value is $22,500 + $4000 = $26,500. d)
. The car’s value depreciates at $2000 per year. c) We can use linear reasoning knowing that 2016 is 2 years prior to 2018 when the car was valued at $14,500. Since the rate of depreciation is $2000 per year it must have been worth 2($2000) = $4000 more in 2016 than in 2018. So the initial value is $22,500 + $4000 = $26,500. d) 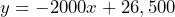 e) 10.75 years from 2016 is 3/4 of the way through 2026.
e) 10.75 years from 2016 is 3/4 of the way through 2026.
 In this section, we will use what we have learned so far to practice skill problems.
In this section, we will use what we have learned so far to practice skill problems.
Skill Exercises
Find the slope of the line between the two points:
- (0, 2) and (6, 4)
- (3, 5) and (4, 3)
- (4, 0) and (–2, 4)
- (0, –3) and (6, 0)
- (–3, -4) and (1, –6)
Write the equation of the line with the given slope and ![]() -intercept:
-intercept:
- 3 and (0, 6)
- –4 and (0, 5)
- 3/2 and (0, –2)
- –4/5 and (0, –4)
- –2/3 and (0, 4/3)
Write the equation of the line that passes through the two points:
- (5, 0) and (0, –5)
- (3, 2) and (4, 5)
- (–3, 4) and (2, –4)
- (-5, 2) and (7, 2)
- (4, 5) and (6, –7)
Show/Hide Answer
- 1/3
- –2
- –2/3
- 1/2
- –1/2