CHAPTER 5: LINEAR EQUATIONS IN ONE VARIABLE
5-1: Variables and Algebraic Expressions
Constants and Variables
The definition of the word constant is never changing; stays the same. In mathematics, a constant is a number; the value of the number never changes. But there are very few things in life that remain constant, so we need a way of describing a value that can change or vary. In mathematics, we use a symbol or a letter to stand in for a quantity that either varies (i.e., it is not constant) or whose value we do not know. Such a symbol is called a variable.
In 1908, German mathematician Felix Klein wrote,[1]
“one may well declare that
real mathematics begins with operations with letters.”
and Polish-American mathematician Alfred Tarski wrote in 1941 that,[2]
“the invention of variables constitutes a turning point
in the history of mathematics.”
Variables are so important in math as they allow mathematical ideas to be communicated clearly and concisely. Variables also make mathematics more generally applicable. For example, to determine the area of a flower bed that measures 5 feet by 2 feet, we can multiply the length by the width to get ![]() . But that multiplication only works when the length is 5 feet and the width is 2 feet. To express the fact that the area of a rectangular two-dimensional space is always found by multiplying its length by its width, we use variables to create a formula:
. But that multiplication only works when the length is 5 feet and the width is 2 feet. To express the fact that the area of a rectangular two-dimensional space is always found by multiplying its length by its width, we use variables to create a formula: ![]() , where
, where ![]() represents area,
represents area, ![]() represents length and
represents length and ![]() represents width. This formula can be used to determine the area of any rectangle provided we know the values for the length and the width.
represents width. This formula can be used to determine the area of any rectangle provided we know the values for the length and the width.
Another benefit is that we may use variables to represent mathematical relations, which makes it easier when solving problems. For example, we may use the letter ![]() to represent the original price of a pair of shoes that we are asked to determine given that they are on sale for $50 after a 20% discount. The quantitative relation can be written in words as,
to represent the original price of a pair of shoes that we are asked to determine given that they are on sale for $50 after a 20% discount. The quantitative relation can be written in words as,
the original price – the discount = the sale price
which, after defining the variable ![]() to represent the unknown original price, can be written symbolically as
to represent the unknown original price, can be written symbolically as
![]()
After performing some algebraic manipulation on the equation, we may then determine the original price ![]() .
.
 Variables, Terms, and Expressions
Variables, Terms, and Expressions
Explore 1 – Variables
- Suppose you buy three combo meals from a fast-food restaurant, where the price of each combo meal is $10.99. Determine the cost of the three meals.
Solution
We can determine the cost in two ways using either multiplication or addition:
multiplication: cost = 3 ![]() $10.99 = $32.97
$10.99 = $32.97
addition: cost = $10.99 + $10.99 + $10.99 = $32.97
Note that the cost is the same whether we use multiplication or addition.
- Suppose you do not know the cost of a combo meal, so you define the variable
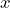 to represent the price of a combo meal. Determine the cost of three meals using multiplication and then using addition. Draw a conclusion from your efforts.
to represent the price of a combo meal. Determine the cost of three meals using multiplication and then using addition. Draw a conclusion from your efforts.
Solution
multiplication: cost = ![]()
addition: cost = ![]()
Since the cost must be the same using multiplication or addition, we can conclude that ![]() .
.
Explore 2 – Addition of variables
A constant multiplied by a variable is equivalent to that variable being added multiple times. For example, ![]() .
.
- Simplify
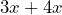
Solution
Since ![]() and
and ![]() ,
, ![]()
- Simplify
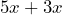
Solution
Since ![]() and
and ![]() ,
, ![]()
- Write a rule that could be used to add
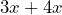 or
or 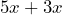
Solution
![]() and
and ![]()
Add the coefficients and keep the common variable.
- Simplify
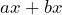
Solution
Using the rule add the coefficients and keep the common variable: ![]()
When a variable is multiplied by a constant, it forms a term. When terms have exactly the same variable(s), they are called like terms. Only like terms can be added and subtracted by adding or subtracting the coefficients and keeping the common variable.
Explore 3 – Expressions
Holly jumped on a dating app and matched with several people. She went on three dinner dates, five coffee dates, and two movie dates. Suppose the variables ![]() and
and ![]() represent the cost of a dinner date, a coffee date, and a movie date, respectively. Use these variables to represent the total amount Holly spent on her dating experiences, if she paid.
represent the cost of a dinner date, a coffee date, and a movie date, respectively. Use these variables to represent the total amount Holly spent on her dating experiences, if she paid.
Solution
Three dinner dates cost ![]() ; five coffee dates cost
; five coffee dates cost ![]() ; two movie dates cost
; two movie dates cost ![]() .
.
So, the total cost = ![]() . These are not like terms so cannot be simplified.
. These are not like terms so cannot be simplified.
When terms with variables are added or subtracted, they form an algebraic expression. Expressions can be simplified (e.g., by adding or subtracting like terms) or they can be evaluated.
Explore 4 – Simplifying and evaluating an expression
A grocery store manager has noticed that certain foods have the same price per item or per pound. The table shows the prices in terms of variables.
| Grocery | Price |
| Apple | $ |
| Cucumber | $ |
| Potato | $ |
| Strawberry | $ |
| Eggs | $ |
| Soda | $ |
- Write an expression that represents the total cost of buying 5 pounds of apples, 2 boxes of strawberries, and 4 cucumbers. Simplify the expression.
Solution
cost of 5 pounds of apples = ![]() ; cost of 2 boxes of strawberries =
; cost of 2 boxes of strawberries = ![]() ; cost of 4 cucumbers =
; cost of 4 cucumbers = ![]()
So, total cost = ![]() The two terms
The two terms ![]() and
and ![]() are like terms and can be combined to
are like terms and can be combined to ![]() .
.
- Suppose
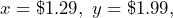 and
and 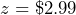 . Determine the total cost of buying 5 pounds of apples, 2 boxes of strawberries, and 4 cucumbers.
. Determine the total cost of buying 5 pounds of apples, 2 boxes of strawberries, and 4 cucumbers.
Solution
To evaluate an expression, we replace each variable with its given value then simplify:
total cost = ![]()
- Write an expression that represents the total cost of buying three 6 packs of soda, 4 boxes of strawberries, and 6 bags of potatoes. Simplify the expression.
Solution
cost of three 6-packs of soda = ![]() ; cost of 4 boxes of strawberries =
; cost of 4 boxes of strawberries = ![]() ; cost of 6 bags of potatoes =
; cost of 6 bags of potatoes = ![]()
So, total cost = ![]() The two terms 3y and 4y are like terms and can be combined to
The two terms 3y and 4y are like terms and can be combined to ![]() .
.
- Suppose
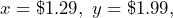 and
and 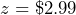 . Determine the total cost of buying three 6 packs of soda, 4 boxes of strawberries, and 6 bags of potatoes.
. Determine the total cost of buying three 6 packs of soda, 4 boxes of strawberries, and 6 bags of potatoes.
Solution
To evaluate an expression, we replace each variable with its given value then simplify:
total cost = ![]()
Constants, Variables, Terms, and Expressions
A constant is a number that never changes value.
A variable is a symbol or letter that represents a quantity that either varies (i.e., it is not constant) or whose value we do not know.
A term is a constant, a variable, or the product or quotient of numbers and variables: ![]()
A coefficient is the constant in a term: ![]() has a coefficient of –7
has a coefficient of –7
Like terms are terms that have exactly the same variables with exactly the same exponents: ![]() and
and ![]() or
or ![]() and
and ![]()
Only like terms can be added or subtracted.
An algebraic expression is a term or the combination of terms: ![]() or
or ![]()
Explore 5 – Evaluating an expression
Weight balance is very important for an airplane to take off, land, and fly safely. Suppose the weight in the front of a plane is represented by the expression ![]() and the weight in the rear is
and the weight in the rear is ![]() . Are the weights balanced between the front and rear if
. Are the weights balanced between the front and rear if ![]() , and
, and ![]() ?
?
Solution
To evaluate the weight, we substitute each variable with its given value.
The weight in the front
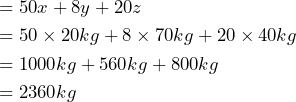
.
The weight in the back
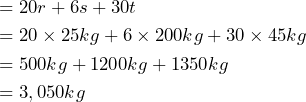
.
The weight of the back is 690kg more than the weight in the front. No, the weights are not balanced.

- What is a variable? Why are variables used?
Show/Hide Answer
A variable is a value holder, which often exists in the form of a lower-case letter. When solving problems, a variable may be used to represent an unknown value, or as a changing amount in a formula.
- What does it mean to “evaluate an expression”?
Show/Hide Answer
To evaluate an expression is to substitute variables in the expression with values/numbers such that the value of the expression with the given values is determined.
Examples
1. A cube is a three-dimensional object that is square on each side. The surface area of each side of a cube equals the square of the length of the side. i.e. if ![]() represents the length of each side, the surface area of any side is
represents the length of each side, the surface area of any side is ![]() .
.
a) Write an expression that represents the surface area of the whole cube.
b) Determine the surface area of the cube when ![]() ,
, ![]() , and
, and ![]()
2. A scientist records a temperature of 50.4°C. Use the expression ![]() to convert this temperature to degrees Fahrenheit.
to convert this temperature to degrees Fahrenheit.
Show/Hide Answer
- a)
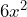 b) 54cm2; 24 ft2; 11.76 in2
b) 54cm2; 24 ft2; 11.76 in2 - 122.72°F
 Writing Algebraic Expressions
Writing Algebraic Expressions
We may use variables to represent any unknown values in a problem, and then translate the mathematical relations in the problem into an algebraic expression. When we introduce a variable into the mix, we must define the variable. This means that we must give the variable a name and tell people what the variable represents.
Explore 6 – Translating to an algebraic expression
KoSze plays a game with his son. KoSze says, “I have a number. I multiply it by 5, then add 10, then take away three times the number, and then divide the result by 2.
Translate KoSze’s words into an algebraic expression, then simplify the expression.
Solution
Let ![]() a number. This is defining the variable.
a number. This is defining the variable.
The number multiplied by 5 is equal to ![]() . Then 10 is added to this:
. Then 10 is added to this:
![]()
Three times the number is equal to ![]() . “Take away” means “subtract”, so, now we have:
. “Take away” means “subtract”, so, now we have:
![]()
Finally we divide by 2:
![]()
The two terms ![]() and
and ![]() are like terms. Therefore,
are like terms. Therefore, ![]()
This leaves us with,
![]()
which can then be further simplified by distributing the 2 to both terms on the numerator:
![]()
Explore 7 – Writing an algebraic expression
Cathy rented a U-Haul truck to move from Denver to Salt Lake City. She was charged $29.99 per day and $0.99 per mile. She rented the truck for three days. As part of a promotion, she got the first 10 miles free.
Translate the problem into an algebraic expression to represent the total amount of the rental fee Cathy paid. Then simplify the expression.
Solution
The first part of the cost comes from the daily rental fee. Cathy rented the truck for three days and the daily rental charge was $29.99 per day. Consequently, the daily rental charge was ![]() .
.
The second part of the cost comes from the mileage she drives. We need to define a variable: let ![]() the number of miles driven.
the number of miles driven.
Since the first 10 miles is free, the total number of miles that was charged is ![]() . Since the charge for mileage was $0.99 per mile, the total mileage charge was
. Since the charge for mileage was $0.99 per mile, the total mileage charge was ![]() .
.
Therefore, the total charge is the sum of the daily rental charge and the mileage charge, which is equal to:
![]() .
.
We can simplify this by distributing the 0.99 to both the m and the –10:
![]()
So, the total charge is:
![]() .
.

- What does it mean to translate a problem to an algebraic expression?
Show/Hide Answer
It means to turn the mathematical relations in a problem into a mathematical expression where the unknown values in the relations are represented by defined variables.
Practice Exercises
- The CDC considers a person having a fever if the person’s body temperature at least 100.4°F. Use the expression
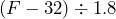 to convert the temperature to degrees Celsius.
to convert the temperature to degrees Celsius. - Bella wants to put a dog run at the side of her house. She knows she has enough room for the width to be 8 feet but she can’t remember the length. a) If she defines
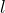 to be the length of the dog run, determine its perimeter in terms of
to be the length of the dog run, determine its perimeter in terms of 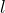 . b) Calculate the perimeter of the dog run if
. b) Calculate the perimeter of the dog run if 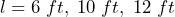 .
. - Leo is buying snacks for a football party. He needs to buy 4 cases of beer, 3 bags of chips, 3 dozen hotdogs, 3 dozen hotdog buns, 2 bottles of salsa. Suppose the beer costs $
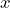 per case, chips cost $
per case, chips cost $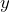 per bag, hotdogs cost $
per bag, hotdogs cost $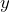 per dozen, hotdog buns cost $
per dozen, hotdog buns cost $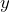 per dozen, and salsa costs $
per dozen, and salsa costs $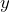 per bottle. a) Write an expression that represents the cost of the snacks, then simplify it. b) Use the simplified expression to determine the cost when
per bottle. a) Write an expression that represents the cost of the snacks, then simplify it. b) Use the simplified expression to determine the cost when 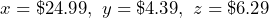
- Michael’s set monthly expenses are rent, electricity, gas, phone, Internet and car payment. His variable expenses are food, personal and household supplies, entertainment, and gas for his car. a) If his rent is $1800 per month, electricity bill is $58 per month, gas bill is $63 per month, phone is $65 per month, Internet is $75 per month, and car payment is $325 per month, what are his total fixed expenses? b) Define a variable for each of his variable expenses, then write an expression to show his total monthly expenses.
- Diane is making naan flatbread. The recipe says to bake the bread at 180° Celsius. The temperature in ° Fahrenheit =
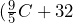 , where
, where 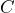 = the temperature in ° Celsius. What temperature should she use to bake her bread?
= the temperature in ° Celsius. What temperature should she use to bake her bread? - Michelle is remodeling her basement and needs to borrow an orbital floor sander to level and etch her concrete floor. The cost is $56 per day. She also need a concrete etcher tool for the sander and that rents for $89 per day. a) If
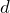 = number of rental days, write an expression to determine the total cost of renting the tools. b) If she rents the tools for 2 days, use your expression to determine the total cost.
= number of rental days, write an expression to determine the total cost of renting the tools. b) If she rents the tools for 2 days, use your expression to determine the total cost.
Show/Hide Answer
- 38°C
- a)
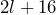 b) 28 ft; 26 ft; 40 ft
b) 28 ft; 26 ft; 40 ft - a)
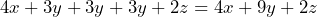 b) $152.05
b) $152.05 - a) $2386 b) Let
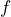 = food costs;
= food costs; 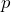 = personal and household expenses;
= personal and household expenses; ![Rendered by QuickLaTeX.com e[latex] = entertainment; [latex]g](https://uen.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-e9c45e30009e90074a50c4fae2d35488_l3.png) = gas. Total monthly expenses =
= gas. Total monthly expenses = 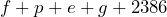 .
. - 356°F
- a) Total cost =
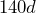 b) $280
b) $280
 In this section, we will take what we have learned and apply the concepts to new situations.
In this section, we will take what we have learned and apply the concepts to new situations.
Perspectives
- The cost of household electricity can be found by evaluating the expression
![Rendered by QuickLaTeX.com [(C - P) · E + B] ·(1+T)](https://uen.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-01ef77c11bc55118f3f883ed00e3bd93_l3.png) , where
, where 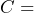 current meter reading;
current meter reading; 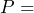 previous meter reading;
previous meter reading; 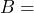 basic charge;
basic charge; 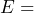 energy charge per kWh; and
energy charge per kWh; and 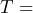 tax rate.
tax rate.
a) What does ![]() represent in the expression?
represent in the expression?
b) What does ![]() represent in the expression?
represent in the expression?
c) Calculate the total charge on this bill: 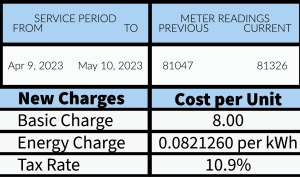
- The cost to rent a Bouncy House for a children’s birthday party is $150 flat fee plus $30 per hour. a) If
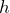 = number of rental hours, write an expression that shows the total cost of renting the bouncy house. b) Use the expression to determine the total cost of renting the bouncy house for 5 hours.
= number of rental hours, write an expression that shows the total cost of renting the bouncy house. b) Use the expression to determine the total cost of renting the bouncy house for 5 hours. - Male crickets and katydids chirp by rubbing their front wings together. Each species has its own chirp and chirping is temperature dependent. To calculate the temperature if you hear a Field Cricket, we can use temperature = 50+[(N-40)/4]. For a Snowy Tree Cricket, temperature = 50 + [(N – 92) / 4.7], and for a Katydid temperature = 60 + [(N – 19) / 3)], where N is the number of chirps per minute. a) Ben and Shana are out camping and hear crickets but have no idea what kind of crickets they are. If they count 44 chirps in 30 seconds what are the possible temperature options? b) SInce crickets generally do not sing at temperatures below 55° F or above 100 °F, what is the most probable type of cricket they are hearing? c) The simplest method is to count the number of chirps in 15 seconds and add 40. Define a variable and write an expression that shows this sum. Use the expression to determine the temperature. How close is this quick method’s temperature to your answers from part a)?
- The distance an object falls under gravity can be calculated using the formula
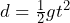 , where
, where 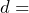 distance in meters,
distance in meters, 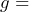 the acceleration due to gravity = 9.9 meters per square second, and
the acceleration due to gravity = 9.9 meters per square second, and 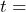 time in seconds. Calculate the depth of a canyon if a stone dropped from the top of the canyon takes 4.2 seconds to hit the floor of the canyon.
time in seconds. Calculate the depth of a canyon if a stone dropped from the top of the canyon takes 4.2 seconds to hit the floor of the canyon. - Blood alcohol content depends on many factors. To calculate the blood alcohol content of an individual we can use the formula
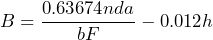 , where
, where 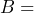 blood alcohol content in ml per dl;
blood alcohol content in ml per dl; 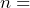 number of drink units,
number of drink units, 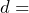 drink volume in milliliters,
drink volume in milliliters, 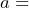 alcohol percentage by volume,
alcohol percentage by volume, 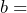 body weight in kilograms,
body weight in kilograms, 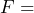 0.58 for males and 0.49 for females, and
0.58 for males and 0.49 for females, and 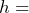 drinking time in hours. a) A 78 kg male drink 2 cans of beer. Each can measures 375 ml with a 4.55% alcohol percentage by volume. He drinks both cans within 30 minutes. Calculate his blood alcohol content. b) To convert from blood alcohol content to blood alcohol percentage, we divide the blood alcohol content by 1000. Calculate this male’s blood alcohol percentage. c) In Utah anyone driving with a 0.05% or greater blood alcohol percentage can be charged with a DUI. Is this male above or below the legal limit to drive? d) A 59 kg female drinks 2 cocktails containing 30 ml each of vodka, which has a 40% alcohol percentage by volume. She drank the cocktails over an hour and a half. Calculate her blood alcohol content. e) Convert this to blood alcohol percentage. f) Would this women be over the legal limit for driving in Utah?
drinking time in hours. a) A 78 kg male drink 2 cans of beer. Each can measures 375 ml with a 4.55% alcohol percentage by volume. He drinks both cans within 30 minutes. Calculate his blood alcohol content. b) To convert from blood alcohol content to blood alcohol percentage, we divide the blood alcohol content by 1000. Calculate this male’s blood alcohol percentage. c) In Utah anyone driving with a 0.05% or greater blood alcohol percentage can be charged with a DUI. Is this male above or below the legal limit to drive? d) A 59 kg female drinks 2 cocktails containing 30 ml each of vodka, which has a 40% alcohol percentage by volume. She drank the cocktails over an hour and a half. Calculate her blood alcohol content. e) Convert this to blood alcohol percentage. f) Would this women be over the legal limit for driving in Utah?
Show/Hide Answer
- a) The amount of electricity used. b) The cost of electricity used. c) $34.28
- a) Total cost =
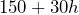 b) $300
b) $300 - a) Field Cricket: 62°F Snowy Tree Cricket: 49°F Katydid: 85°F b) Field Cricket or Katydid b) Let
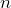 = number of chirps in 15 seconds. Temperature =
= number of chirps in 15 seconds. Temperature = 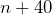 = 66°F. This closest to the Field Cricket calculation.
= 66°F. This closest to the Field Cricket calculation. 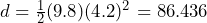 The canyon is about 86 meters deep.
The canyon is about 86 meters deep.- a)
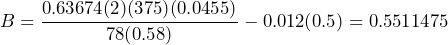 His blood alcohol content is approximately 0.55 b) 0.055% c) above d)
His blood alcohol content is approximately 0.55 b) 0.055% c) above d) 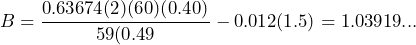 Her blood alcohol content is about 1.04 e) 0.014% f) no
Her blood alcohol content is about 1.04 e) 0.014% f) no
 In this section, we will use what we have learned so far to practice skill problems.
In this section, we will use what we have learned so far to practice skill problems.
Skill Exercises
Evaluate the expression:
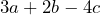 when
when 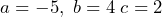
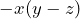 when
when 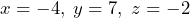
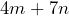 when
when 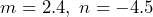
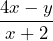 when
when 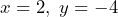
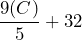 when
when 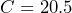
SImplify the expression:
Show/Hide Answer
- –15
- 36
- 21.9
- 64
- 68.9
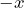
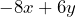
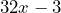
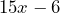
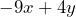
a number that does not change
a symbol that represents a quantity in a mathematical expression that can be changed
an equation or rule that relates variables
a connection between the values of two sets
a constant; a variable; or the product (or quotient) of constants and variables
terms with exactly the same variables with exactly the same exponents
the number multiplied onto a variable; the constant in a term
a variable that is common to two or more terms
a mathematical phrase where terms are combined using operations
calculate the value

