CHAPTER 1: NUMBER SENSE
1-2: The Power of 10
Decimals
The decimal number system is a base-10 number system that uses positional place-values. A base-10 number system counts in groups of 10 and uses only 10 digits to represent any number. The 10 digits we use are: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Place-value in a decimal number tells us how many groups of ten we are dealing with. Every place-value gets ten times bigger as we move to the left in a decimal number and every place-value gets ten times smaller as we move to the right in a decimal number.

 Place-Value
Place-Value
Explore 1 – The relationship between places
Explain how the name of each place-value shows that it is ten times the value of its adjacent place-value to the right, and consequently one-tenth the value of its adjacent value to the left.
Solution
The number 100 represents one hundred and has a 1 in the hundreds place. 100 is ten times the number 10, which has a 1 in the tens place. One thousand is represented as 1,000 with the 1 in the thousands place and is ten times 100. Ten-thousand is represented by 10,000 and means 10 times one thousand. One hundred-thousand is represented by 100,000 and is ten times 10,000.
Decimals after the point represent fractions of a whole. The number 0.1 is read one-tenth which is ![]() the value of 1. Equivalently, 1 is ten times the value of one-tenth. 0.01 is read one-hundredth since the 1 is in the hundredths place and is
the value of 1. Equivalently, 1 is ten times the value of one-tenth. 0.01 is read one-hundredth since the 1 is in the hundredths place and is ![]() the value of 0.1. Likewise, 0.001 has a 1 in the thousandths place so is read one-thousandth and is
the value of 0.1. Likewise, 0.001 has a 1 in the thousandths place so is read one-thousandth and is ![]() the value of 0.01. This pattern continues with 0.0001 representing one-ten-thousandth, which is
the value of 0.01. This pattern continues with 0.0001 representing one-ten-thousandth, which is ![]() the value of 0.001, etc.
the value of 0.001, etc.
Explore 2 – Sets of three
People like to add a comma for every three places to the left of the decimal point when writing large numbers of 10,000 or more. For example, the population of the United States was 335,967,423 as of January 25th, 2023.
- How do you read the number 335,967,423?
Solution
The number 335 formed by the digits before the first comma is read as three hundred thirty-five, but its last digit is in the millions place. Consequently, the digits 335 represent three hundred thirty-five million. The three digits 967 form the number nine hundred sixty-seven, but its last digit is in the thousands place, so 967 represents nine hundred sixty-seven thousand. The three digits 423 form the number four hundred twenty-three. Putting these sets of numbers together we have, three hundred thirty-five million, nine hundred sixty-seven thousand, four hundred twenty-three.
- What is the function of the two commas in the expression 335,967,423? Explain your reasoning.
Solution
The two commas separate three different sets of place-values. The commas are used to make reading the number easier as it splits the number into sets of ones, tens, and hundreds of the place-value before the comma.
Explore 3 – Decimal places
In life, the measure of length in the metric system follows the base-10 number system. Latin and Greek root prefixes are attached to the basic unit of meter to represent the different place-values.
| Greek roots | Base unit | Latin Roots | |||||
| Length | Kilometer | hectometer | dekameter | meter | decimeter | Centimeter | millimeter |
| Place-value | thousands | hundreds | tens | ones | tenths | hundredths | thousandths |
- The value of one decimeter is how many times the value of one meter?
Solution
Decimeter is one place to the right of meter so one decimeter is 0.1 times the value of one meter.
- How many centimeters are in one meter?
Solution
Centimeter lies 2 places to the right of meter so there are 100 centimeters in one meter.
- The value of one kilometer is how many times the value of one meter?
Solution
Kilometer lies 3 places to the left of meter so one kilometer is 1000 times the value of one meter.
- Write 1 decimeter in terms of meter as a decimal number.
Solution
Decimeter is one-tenth of a meter: 0.1 meter
- Write 1 kilometer in terms of meter as a decimal number.
Solution
Kilometer lies 3 places to the left of meter so 1 kilometer = 1000 meters
- Write 23 centimeters in terms of meter as a decimal number.
Solution
Centimeter lies 2 places to the right of meter, so 23 centimeters = 0.23 meters
- Write 1 millimeter in terms of meter as a decimal number.
Solution
Millimeter lies 3 places to the right of meter so 1 millimeter = 0.001 meters
- Write 90 millimeters in terms of meter as a decimal number.
Solution
90 millimeters = 0.090 meters
Examples
1. The monetary units of dollar, dime, and cent follow the place-value rules of the base-10 number system.
a) Write 2 dollars and 57 cents as a decimal number.
b) Write two hundred fifty-seven dollars and eighty-five cents as a decimal number.
c) What does the word ‘and’ represent in a spoken decimal number?
Show/Hide Answer
a) $2.57 b) $257.85 c) The decimal point.
2. Convex lenses are used in eyeglasses for correcting farsightedness while concave lenses correct nearsightedness. Concave lenses have a positive focal length, while convex lenses have a negative focal length.
Don wears contact lenses to correct his vision. The prescription says -1.65 for his left eye and -1.75 for his right eye.
What is the place-value of the digit 5 in either prescription?
Show/Hide Answer
The 5 sits two places after the decimal point so is in the hundredths place

- What is the numerical relationship between two adjacent digits (places) in a decimal number?
Show/Hide Answer
The digit to the left is in a place where its value is 10 times the place-value of the digit to the right.
- Is there any number you know that cannot be represented by the base-10 number system?
Show/Hide Answer
No. Any number can be represented by the base-10 number system.
- What is the difference between digits to the left of the decimal point and digits to the right of the decimal point?
Show/Hide Answer
The number formed by the digits to the left of the decimal point represents an integer value. The number formed by the digits to the right of the decimal point represents a fraction of a whole.
- What is the purpose of the decimal point?
Show/Hide Answer
The decimal point separates the integer value of the number from the fractional value of the number.
 Standardized Decimals
Standardized Decimals
While it is common in the U.S. to use commas every 3 decimal places before the decimal point, and use a period for the decimal point, that is not the case in other parts of the world. In Europe, for example, the commas and period are reversed. So, ![]() in Europe is equivalent to
in Europe is equivalent to ![]() in the U.S.
in the U.S.
“In decimal numbers, the comma (French practice) or the dot (British practice) is used only to separate the integral part of numbers from the decimal part. Numbers may be divided in groups of three in order to facilitate reading; neither dots nor commas are ever inserted in the spaces between groups.”[1]Indeed, in 1948, and again in 2018, the GCPM standardized the printing of decimal numbers under the metric system to use a small space rather than a comma or a period as space-value separators.
So, if you see a number written as ![]() do not be surprised. Notice also that a small space separator is also used after the decimal point to separate the digits into groups of three.
do not be surprised. Notice also that a small space separator is also used after the decimal point to separate the digits into groups of three.
 Exponents & The Power of 10
Exponents & The Power of 10
Exponents
Writing repeated addition is tiresome, for example, ![]() . Repeated addition of a number may be expressed by multiplication. For example, adding three 5s (5+5+5) may be expressed as
. Repeated addition of a number may be expressed by multiplication. For example, adding three 5s (5+5+5) may be expressed as ![]() . The number 5 is added to itself three times. Therefore, we say 3 “times” 5 or 3 “
. The number 5 is added to itself three times. Therefore, we say 3 “times” 5 or 3 “![]() ” 5. Likewise,
” 5. Likewise, ![]() .
.
Is there a similar way to write repeated multiplication of a number? Afterall, writing repeated multiplication is just as tiresome and prone to mistakes as writing repeated addition. Rather than writing, ![]() , we can use an exponent to indicate how many times the number is multiplied by itself. An exponent is a small number written to the top right of the number being multiplied. We write
, we can use an exponent to indicate how many times the number is multiplied by itself. An exponent is a small number written to the top right of the number being multiplied. We write ![]() . The number that is repeatedly multiplied (in this case 5) is called the base. The exponent number 3 is the number of times the base is multiplied by itself. For example,
. The number that is repeatedly multiplied (in this case 5) is called the base. The exponent number 3 is the number of times the base is multiplied by itself. For example, ![]() since the base 4 is multiplied by itself a total of 5 times.
since the base 4 is multiplied by itself a total of 5 times.
The Power of 10
Explore 4 – The power of 10 with positive exponents
One hundred dollars is 10 lots of 10 dollars: ![]() . One thousand dollars is 10 lots of one hundred dollars:
. One thousand dollars is 10 lots of one hundred dollars: ![]() . Likewise, ten-thousand dollars are 10 lots of one thousand dollars:
. Likewise, ten-thousand dollars are 10 lots of one thousand dollars: ![]() . We can continue this pattern indefinitely: One hundred-thousand dollars is 10 lots of ten-thousand dollars:
. We can continue this pattern indefinitely: One hundred-thousand dollars is 10 lots of ten-thousand dollars: ![]() .
.
Write one hundred, one thousand, ten-thousand, one hundred-thousand, one million, ten-million, one hundred-million, one billion, and one trillion dollars in exponential expressions with 10 as the base.
Solution
- One hundred dollars
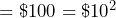
- One thousand dollars
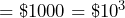
- Ten-thousand dollars
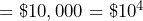
- One hundred-thousand dollars
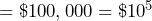
- One million dollars
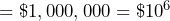
- Ten-million dollars
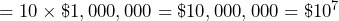
- One hundred-million dollars
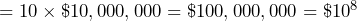
- One billion dollars
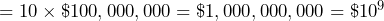
- One trillion dollars
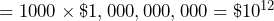
Did you notice that every time a power of 10 is multiplied by another 10, the exponent increases by 1? For example, ![]() . Since it is multiplied by itself just once,
. Since it is multiplied by itself just once, ![]() can be written
can be written ![]() . So,
. So, ![]() . Also,
. Also, ![]() (see 9 in Explore 4). There are two patterns here. First, the number of zeros in a number that is a power of 10 is equal to the exponent. For example,
(see 9 in Explore 4). There are two patterns here. First, the number of zeros in a number that is a power of 10 is equal to the exponent. For example, ![]() has four zeros and is equal to
has four zeros and is equal to ![]() . The second pattern is that when we multiply powers of 10 (e.g.
. The second pattern is that when we multiply powers of 10 (e.g. ![]() ) we can add the exponents to get the exponent of the product:
) we can add the exponents to get the exponent of the product: ![]() .
.
Explore 5 – The power of 10 with negative exponents
Just as multiplying by 10 causes an increase by 1 in the exponent on a power of 10, dividing by 10 causes a decrease by 1 in the exponent. To illustrate, one tenth of one thousand dollars is $1000 divided by 10 which equals $100: ![]() . That is
. That is ![]() : the exponent decreases by 1 from 3 to 2 . Likewise, one tenth of one hundred dollars is $100 divided by 10, which is $10. The exponent decreases by 1 again:
: the exponent decreases by 1 from 3 to 2 . Likewise, one tenth of one hundred dollars is $100 divided by 10, which is $10. The exponent decreases by 1 again: ![]() .
.
- What is the exponential expression for the number that is one-tenth of 10?
Solution
One-tenth of 10 means ![]() . The exponents are subtracted.
. The exponents are subtracted.
- Since
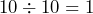 , what does
, what does 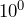 equal?
equal?
Solution
![]() and
and ![]() , so
, so ![]() .
.
- What is the exponential expression for the number that is one-tenth of 1? Write this number as a decimal number.
Solution
One-tenth of 1 means ![]() . The exponent is decreased by 1. As a decimal,
. The exponent is decreased by 1. As a decimal, ![]() . So,
. So, ![]() .
.
- What is the exponential expression for the number that is one-tenth of
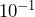 ? Write this number as a decimal number.
? Write this number as a decimal number.
Solution
One-tenth of ![]() means
means ![]() . The exponent is decreased by 1. As a decimal,
. The exponent is decreased by 1. As a decimal, ![]() . So,
. So, ![]() .
.
- What is the exponential expression if the number
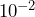 decreases 10 times? Write this number as a decimal number.
decreases 10 times? Write this number as a decimal number.
Solution
One-tenth of ![]() means
means ![]() . The exponent is decreased by 1. As a decimal,
. The exponent is decreased by 1. As a decimal, ![]() . So,
. So, ![]() .
.
Did you notice the pattern that dividing a power of 10 by 10 decreases the exponent by 1? Also, a power of 10 with a negative exponent means we are dealing with a fraction so it belongs to the right of the decimal place. Indeed, the absolute value of the exponent tells us the number of places after the point where the 1 lies. For example, in ![]() , the 1 lies in the 5th place after the point where
, the 1 lies in the 5th place after the point where ![]() .
.
Properties of Powers of 10
Exponent of 1
Any number to the power 1 equals the number.
![]()
Zero Exponent
Any non-zero number to the power zero equals 1.
![]()
Product Rule
Two or more exponential expressions with the same base can be multiplied by
keeping the common base and adding the exponents.
![]()
Quotient Rule
Two exponential expressions with the same base can be divided by
keeping the common base and subtracting the exponents.
![]()
Negative Exponents
When an exponential expression has a negative exponent
the number is a fraction of a whole.
![]() with the digit
with the digit ![]() in the
in the ![]() th place after the decimal point
th place after the decimal point
Explore 6 – Multiplication by powers of 10
Precious tells Brandon a fast way to understand multiplying by a power of 10. She says, if you have 10, which is ![]() , it becomes
, it becomes ![]() if you multiply it by 10. If you multiply
if you multiply it by 10. If you multiply ![]() by 10, it becomes
by 10, it becomes ![]() , then multiply by 10 again to get
, then multiply by 10 again to get ![]() , then
, then ![]() if you keep multiplying by 10 and so on.
if you keep multiplying by 10 and so on.
- What do you get if you multiply
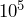 by
by 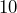 ? Write your answer as a power of
? Write your answer as a power of 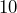 and as a decimal.
and as a decimal.
Solution
Since ![]() , multiplying it by
, multiplying it by ![]() just adds another zero to the answer. So,
just adds another zero to the answer. So, ![]() . Adding one extra zero is equivalent to adding 1 to the power on the
. Adding one extra zero is equivalent to adding 1 to the power on the ![]() .
. ![]() .
.
- How do you write
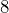 multiplied by
multiplied by 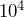 as a decimal?
as a decimal?
Solution
![]() is equivalent to
is equivalent to ![]() . This is like writing the number
. This is like writing the number ![]() and attaching four zeros.
and attaching four zeros.
- How do you multiply
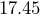 by
by 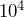 ? What happens to the decimal point?
? What happens to the decimal point?
Solution
![]() . Using a calculator we get
. Using a calculator we get ![]() . The decimal point in
. The decimal point in ![]() gets moved 4 places to the right.
gets moved 4 places to the right.
- Is there a rule for multiplying by a power of 10?
Solution
To multiply a number by a power of 10, we move the decimal point in the number to the right the same number of places as the power.
- What is
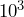 multiplied by
multiplied by 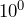 ?
?
Solution
![]() means we move the decimal point in
means we move the decimal point in ![]() zero places to the right. So,
zero places to the right. So, ![]() . When multiplying by
. When multiplying by ![]() to the power of zero, the decimal point doesn’t move. The only number we can multiply by that doesn’t change the number is
to the power of zero, the decimal point doesn’t move. The only number we can multiply by that doesn’t change the number is ![]() . So,
. So, ![]() .
.
- What is
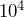 multiplied by
multiplied by 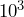 ?
?
Solution
![]() and
and ![]() . So,
. So, ![]() . Since there are seven zeros after the
. Since there are seven zeros after the ![]() ,
, ![]() .
.
- Write a rule that explains how to multiply two powers of
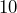 .
.
Solution
To multiply two powers of ![]() , we keep the base
, we keep the base ![]() and add the exponents.
and add the exponents.
- What is
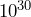 multiplied by
multiplied by 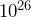 ?
?
Solution
We add the powers, so ![]() .
.

- How is the positive power of 10 (e.g.,
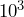 ) related to the number of zeros to the left of the decimal point?
) related to the number of zeros to the left of the decimal point?
Show/Hide Answer
![]() and
and ![]() so the exponent in the power of 10 tells us the number of zeros to write to the left of the decimal point.
so the exponent in the power of 10 tells us the number of zeros to write to the left of the decimal point.
- How is the positive power of 10 (e.g.,
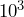 ) related to the place-value of the digit 1 to the left of the decimal point?
) related to the place-value of the digit 1 to the left of the decimal point?
Show/Hide Answer
![]() and
and ![]() so the place-value of the digit 1 is one more than the positive power on the 10.
so the place-value of the digit 1 is one more than the positive power on the 10.
- How is the negative power of 10 (e.g.,
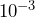 ) related to the number of zeros to the right of the decimal point?
) related to the number of zeros to the right of the decimal point?
Show/Hide Answer
In ![]() , there are 2 zeros after the point. In
, there are 2 zeros after the point. In ![]() , there are 4 zeros after the point. So the number of zeros after the decimal point is one less than the absolute value of the negative power.
, there are 4 zeros after the point. So the number of zeros after the decimal point is one less than the absolute value of the negative power.
- How is the negative power of 10 (e.g.,
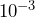 ) related to the place-value of the digit 1 to the right of the decimal point?
) related to the place-value of the digit 1 to the right of the decimal point?
Show/Hide Answer
In ![]() , the digit 1 is 3 places after the point. In
, the digit 1 is 3 places after the point. In ![]() , the digit 1 is 5 places after the point. So we use the absolute value of the negative power to determine the place-value of the digit 1.
, the digit 1 is 5 places after the point. So we use the absolute value of the negative power to determine the place-value of the digit 1.
Practice Exercises
Precious tells Brandon a fast way to understand negative exponents. She says, if you have ![]() , or
, or ![]() , it becomes
, it becomes ![]() if you divide it by
if you divide it by ![]() . If you divide
. If you divide ![]() by
by ![]() again, it becomes
again, it becomes ![]() , then
, then ![]() , then
, then ![]() ,
, ![]() ,
, ![]() if you keep dividing it by
if you keep dividing it by ![]() .
.
- What would
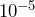 equal as a decimal?
equal as a decimal? - What would
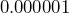 equal as a power of
equal as a power of 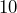 ?
? - What is
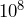 divided by
divided by 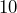 ?
? - What is
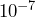 divided by
divided by 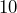 ?
? - What is
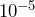 divided by
divided by 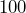 ?
? - What is
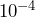 multiplied by
multiplied by 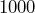 ?
? - Write a rule that governs multiplying or dividing by powers of 10?
Show/Hide Answer
- 0.00001
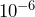
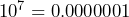
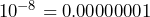
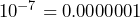
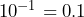
- To multiply by a power of 10, keep the base 10 and add the exponents. To divide by a power of 10, keep the base and subtract the exponents.
 National Debt
National Debt
People don’t have a strong intuitive sense of how much bigger a trillion is than a billion, or a billion is than a million. As an example, a million seconds is about 11.6 days. A billion seconds is about 31.7 years. A trillion seconds is about 31,688 years.
The U.S. national debt can be found at https://www.usdebtclock.org.
- Is the current national debt measured in millions, billions, or trillions of dollars?
- Koa’s annual salary is $100,000. How many years would it take Koa to payoff the national debt?
- How much would each of the billionaires in the U.S. have to donate to be able to pay off the national debt?
 In this section, we will take what we have learned and apply the concepts to new situations.
In this section, we will take what we have learned and apply the concepts to new situations.
Perspectives
 The table on the right shows metric prefixes in common use.
The table on the right shows metric prefixes in common use.
- A Youtuber bought a one-terabyte (
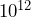 -bytes) external drive for storing the videos she made. She typically makes 10-minute videos for her channel. A 10-minute video takes up about 100 megabytes (
-bytes) external drive for storing the videos she made. She typically makes 10-minute videos for her channel. A 10-minute video takes up about 100 megabytes (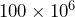 )-bytes of storage.
)-bytes of storage.
a) How many 10-minute videos can be stored on a one-terabyte external drive?
b) How many 10-minute videos can be stored on a 5-terabyte external drive?
- The most valuable substance on earth is Botulinum toxin which is used to create Botox. It values at $1.5 trillion per kilogram. In each vial of Botox, there is just under 1 nanogram of the toxin.
a) How many vials can be made from 1 kilogram of Botulinum toxin?
b) What is the cost of 1 nanogram of the toxin?
- Nuclear bombs are discussed in megatons or kilotons. In this context, ton refers not to the weight of the bomb but to the explosive yield of a ton of TNT. The only two nuclear bombs used in war were dropped on Japan in 1945. The first bomb hit Hiroshima on August 6th and the second bomb hit Nagasaki on August 9th. The damage was so extensive and horrific that some believe it ended the war in the Pacific. The first bomb, “Little Boy,” had an explosive yield of 15 kilotons. The second bomb, “Fat Man,” had an explosive yield of 21 kilotons. As of 2020, the US had 320 gravity bombs with the following designations and yields: B61-7 (360 kilotons); B61-11 (400 kilotons); B83-1 (1200 kilotons). [2]
a) How many tons of TNT would have the same explosive yield as “Little Boy”?
b) How many tons of TNT would have the same explosive yield as “Fat Man”?
c) How many times is the B61-7 as big as the “Fat Man” in terms of explosive yield?
d) How many times is the B83-1 as big as the “Fat Man” in terms of explosive yield?
e) Estimate the destructive power of the US arsenal of gravity bombs in terms easier to grasp than kilotons.
Show/Hide Answer
-
- a) Ten thousand 10-minute videos may be stored on the external drive. b) Fifty thousand 10-minute videos.
- a) There are 1012 nonograms in 1 kilogram. b) It costs $0.015 for 1 nanogram of the toxin.
- a) 15,000 tons b) 21,000 tons c) 17.1 times as big d) 57.1 times as big e) Total annihilation
 Currency
Currency
A packet of one hundred $100 bills, currently the largest U.S. bill in circulation, is less than ½ inch thick. It would fit easily in your pocket.
- How much money is there in a stack of 100 $100 bills?
- How many of these stacks would you need to make $1 billion?
- How high would the stack be to make $1 billion?
- Compare this height to something tangible.
- How many of these stacks would you need to make $1 trillion?
- Why is the $100 bill the largest U.S. bill in circulation?
 In this section, we will use what we have learned so far to practice skill problems.
In this section, we will use what we have learned so far to practice skill problems.
Skills Practice
Evaluate the expression. Write the answer as a power of 10 and as a decimal.
Show/Hide Answer
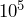 ; 100,000
; 100,000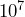 ; 10,000,000
; 10,000,000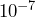 ; 0.0000001
; 0.0000001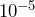 ; 0.00001
; 0.00001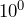 ; 1
; 1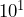 ; 10
; 10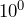 ; 1
; 1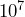 ; 10,000,000
; 10,000,000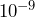 ; 0.000000001
; 0.000000001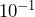 ; 0.1
; 0.1- 4000
- 7,000,000
- 0.03
- 4,500,000
- 0.00028
Real numbers written using a base 10 place-value system.
The international decimal system of weights and measures.
General Conference on Weights and Measures (CGPM, Conférence Générale des Poids et Mesures). The CGPM is the primary intergovernmental treaty organization responsible for the SI (metric system), representing nearly 50 countries.
a quantity representing the power to which a given number or expression is to be raised, usually expressed as a raised symbol beside the number or expression.

