CHAPTER 7: EXPONENTIAL AND LOGARITHMIC GROWTH
7-5: Solving Exponential Equations using Logarithms
Exponential Equations
The exponential equation ![]() is the standard form for the equation of any exponential pattern. We can also write the equation as
is the standard form for the equation of any exponential pattern. We can also write the equation as ![]() in terms of the rate of change
in terms of the rate of change ![]() . When we have a specific equation, for example
. When we have a specific equation, for example ![]() , we can determine the value of
, we can determine the value of ![]() by substituting a given value for
by substituting a given value for ![]() . For example, if
. For example, if ![]() ,
, ![]() becomes
becomes ![]() , which evaluates to
, which evaluates to ![]() . But how do we determine an
. But how do we determine an ![]() -value given a specific
-value given a specific ![]() -value? For example, how do we solve the equation
-value? For example, how do we solve the equation ![]() ? In section 7-2, we used the graph of the equation to approximate the
? In section 7-2, we used the graph of the equation to approximate the ![]() -value. But how do we solve such an equation algebraically? We have to introduce logarithms. Logarithms allow us to solve an equation for the value of the exponent.
-value. But how do we solve such an equation algebraically? We have to introduce logarithms. Logarithms allow us to solve an equation for the value of the exponent.
 The Definition of Logarithms
The Definition of Logarithms
Logarithm is the word used to represent the value of an exponent to which a base number must be raised to yield a specific number. Since exponential expressions such as ![]() have a base (i.e., 2), logarithms have the same base. And since logarithm is a rather long word to have to write, it is abbreviated to
have a base (i.e., 2), logarithms have the same base. And since logarithm is a rather long word to have to write, it is abbreviated to ![]() where
where ![]() is the base of the logarithm.
is the base of the logarithm.
Equivalent Forms
The first equation, ![]() , is solved for
, is solved for ![]() in terms of
in terms of ![]() while the second equation,
while the second equation, ![]() , is solved for
, is solved for ![]() in terms of
in terms of ![]() . Parentheses are often used around the argument of a logarithm for clarity.
. Parentheses are often used around the argument of a logarithm for clarity.
Explore 1 – Logarithms base 10
A population of bed bugs multiplies by 10 every day. If the population started with 3 bedbugs, the equation that represents this scenario is ![]() , where
, where ![]() = time in days and
= time in days and ![]() = the population of bedbugs.
= the population of bedbugs.
- How long will it take to reach a population of 300 bedbugs?
Solution
We replace ![]() in the equation and solve for
in the equation and solve for ![]() :
:
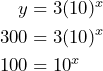
In the last step we divided both sides of the equation by 3 to simplify. Now we have two choices. We can either rewrite the equation using logarithms: ![]() or we can recognize that
or we can recognize that ![]() , therefore
, therefore ![]() meaning that
meaning that ![]() .
.
Notice that this means that ![]() because
because ![]() .
.
It will take 2 days for the population of bedbugs to reach 300.
- How long will it take the population to reach 30,000?
Solution
We replace ![]() in the equation and solve for
in the equation and solve for ![]() :
:
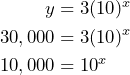
In the last step we divided both sides of the equation by 3 to simplify. Now we have two choices. We can either rewrite the equation using logarithms: ![]() or we can recognize that
or we can recognize that ![]() , therefore
, therefore ![]() meaning that
meaning that ![]() .
.
Notice that this means that ![]() because
because ![]() .
.
It will take 4 days for the population of bedbugs to reach 30,000.
A logarithm with a base of 10 (e.g., ![]() ) is called a common logarithm. The English mathematician Henry Briggs converted the Scottish mathematician John Napier’s 1614 logarithms to base 10 in 1615 and pioneered their use; a multiple of 10 was most advantageous for calculations performed by engineers. Since base 10 was so commonly used, the common logarithm began to be written simply as
) is called a common logarithm. The English mathematician Henry Briggs converted the Scottish mathematician John Napier’s 1614 logarithms to base 10 in 1615 and pioneered their use; a multiple of 10 was most advantageous for calculations performed by engineers. Since base 10 was so commonly used, the common logarithm began to be written simply as ![]() with an assumption that the base was 10. Common logarithms are found on scientific calculators using the
with an assumption that the base was 10. Common logarithms are found on scientific calculators using the ![]() button.
button.
To calculate a common logarithm we input the number first then press the ![]() button.
button.
For example, to evaluate ![]() , we input
, we input ![]() and get the answer
and get the answer ![]() .
.
This means that ![]() and shows that an exponent does not have to be a whole number.
and shows that an exponent does not have to be a whole number.
Another logarithm that is available on a scientific calculator is the natural logarithm, ![]() . The base of the natural logarithm is the irrational constant
. The base of the natural logarithm is the irrational constant ![]() . The natural logarithm of
. The natural logarithm of ![]() is the power to which
is the power to which ![]() would have to be raised to equal
would have to be raised to equal ![]() . Rather than writing
. Rather than writing ![]() the abbreviation
the abbreviation ![]() is used. i.e.
is used. i.e. ![]() .
.
Explore 2 – Common logarithms
The number of views of an online video grows 10 times every day. When the video was posted there was 1 view. Today, there were 1 billion views. How many days has the video been online since it was posted?
Solution
We start by writing an exponential equation to represent the number of views ![]() over time
over time ![]() :
: ![]() or
or ![]() .
.
Now we substitute the value 1 billion for the variable ![]() because the variable
because the variable ![]() represents the number of views.
represents the number of views.
![]() .
.
To solve this equation, we have two choices:
1) Write 1 billion as ![]() so that the equation becomes
so that the equation becomes ![]() . Since each exponential expression has the same base (i.e., 10) the exponents must be equal:
. Since each exponential expression has the same base (i.e., 10) the exponents must be equal: ![]()
or
2) Write the exponential equation in equivalent logarithmic form:
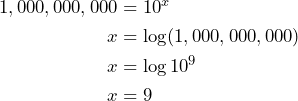
Either way, the video has been posted for 9 days.
Explore 3 – Common logarithms
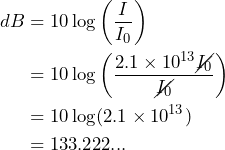
Since this is greater than 85dB, hearing protection should be worn.
.

- What is a logarithm? Under what situation would you use logarithms? Give an example.
Show/Hide Answer
A logarithm is the word used to represent the value of an exponent to which a base number must be raised to yield a specific number. We use logarithms when we want to know the value of the exponent given a base and the result. For example, since ![]() ,
, ![]() . If we want to determine the value of
. If we want to determine the value of ![]() such that
such that ![]() , then
, then ![]() .
.
 The natural number, e
The natural number, e
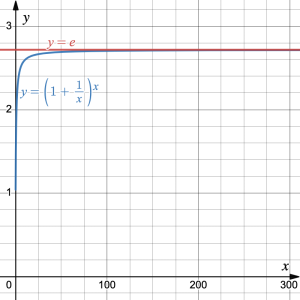
Consider the equation ![]()
- Use a calculator to complete the table:
| 1 | 2 | 5 | 10 | 100 | 1000 | 10,000 | 100,000 | 1,000,000 | |
|---|---|---|---|---|---|---|---|---|---|
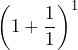 |
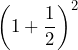 |
||||||||
| 2 | 2.25 |
- What do you notice about the value of
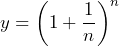 ?
? - Use the desmos graphing calculator to graph
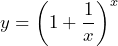 On the same graph, graph the horizontal line
On the same graph, graph the horizontal line 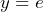 .
. - What do you notice about the value of
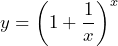 as the value of
as the value of  increases?
increases? - What do the table and graph tell us about the value of
 ?
? - How does the asymptote of the graph explain that
 is an irrational number?
is an irrational number?
Show/Hide Answers
1.
| 1 | 2 | 5 | 10 | 100 | 1000 | |
|---|---|---|---|---|---|---|
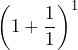 |
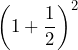 |
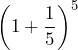 |
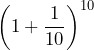 |
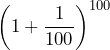 |
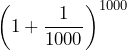 |
|
| 2 | 2.25 | 2.48832 | 2.5935424601 | 2.704813829421526 | 2.716923932235892 |
| 1000 | 10,000 | 100,000 | 1,000,000 |
|---|---|---|---|
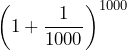 |
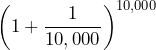 |
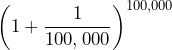 |
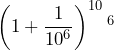 |
| 2.716923932235892 | 2.718145926825225 | 2.71826823717449 | 2.718280469319377 |
2. The value of ![]() seems to settle to a number close to 2.7182 as
seems to settle to a number close to 2.7182 as ![]() increases.
increases.
4. The graph of ![]() gets closer and closer to the line
gets closer and closer to the line ![]() as
as ![]() increases. The line
increases. The line ![]() is an asymptote to the graph of
is an asymptote to the graph of ![]()
5. The value of ![]() is equal to the value of
is equal to the value of ![]() as
as ![]() gets closer to infinity, and can be approximated by the value 2.71828.
gets closer to infinity, and can be approximated by the value 2.71828.
6. The asymptote can never be crossed so the value of ![]() can never quite reach
can never quite reach ![]() . However, as
. However, as ![]() gets closer to infinity, the graph gets closer to
gets closer to infinity, the graph gets closer to ![]() . This means that the distance between the graph and the asymptote is getting closer and closer to zero but will never reach zero. So the value of
. This means that the distance between the graph and the asymptote is getting closer and closer to zero but will never reach zero. So the value of ![]() must have never ending digits, and therefore be irrational.
must have never ending digits, and therefore be irrational.
The constant ![]() is known as the natural number and there are many ways of calculating
is known as the natural number and there are many ways of calculating ![]() . However, since
. However, since ![]() is an irrational number, it is represented by a decimal whose digits go on forever without repeating. Pressing the key
is an irrational number, it is represented by a decimal whose digits go on forever without repeating. Pressing the key ![]() on a calculator gives an approximation of 2.718281818459045, but
on a calculator gives an approximation of 2.718281818459045, but ![]() has been calculated to trillions of digits.
has been calculated to trillions of digits.
The first references to the constant were published in 1618 in the table of an appendix of a work on logarithms by Scottish mathematician John Napier. However, this did not contain the constant itself, but simply a list of logarithms to the base ![]() .
.
The constant itself was introduced by Swiss mathematician Jacob Bernoulli in 1683, for solving the problem of continuous compounding of interest. In his solution, the constant occurs as
![]()
where ![]() represents the fraction of the year on which the compound interest is evaluated (for example,
represents the fraction of the year on which the compound interest is evaluated (for example, ![]() for a month). The notation
for a month). The notation
![]()
means the limit value of the expression ![]() as
as ![]() gets closer and closer to infinity.
gets closer and closer to infinity.
The constant was originally named ![]() after Bernoulli, but Swiss mathematician Leonhard Euler started using the letter
after Bernoulli, but Swiss mathematician Leonhard Euler started using the letter ![]() around 1727 and the letter
around 1727 and the letter ![]() stuck.[1]
stuck.[1]
Explore 4 – Natural Logarithms
When an investment amount of ![]() gains compound interest continuously (as opposed to once per month or once per year etc.) at a rate of
gains compound interest continuously (as opposed to once per month or once per year etc.) at a rate of ![]() per year, the equation
per year, the equation ![]() can be used to determine the amount,
can be used to determine the amount, ![]() in the account at any time,
in the account at any time, ![]() in years. Matt and Braidy invest $10,000 into an account paying 5.25% interest compounded continuously when their son Bennett is born. The invested money is Bennett’s college education fund.
in years. Matt and Braidy invest $10,000 into an account paying 5.25% interest compounded continuously when their son Bennett is born. The invested money is Bennett’s college education fund.
- How much money will be in the account when Bennett turns 10 years old?
Solution
We are told that ![]() and
and ![]() , so the equation with the given interest rate and investment amount is:
, so the equation with the given interest rate and investment amount is:
![]()
When Bennett turns 10, ![]() , so substituting
, so substituting ![]() into the equation yields:
into the equation yields:
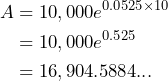
Therefore, there will be $16,904.58 in the account when Bennett turns 10.
- How much money will be in the account when Bennett turns 18 years old?
Solution
When Bennett turns 18, ![]() , so substituting
, so substituting ![]() into the equation yields:
into the equation yields:
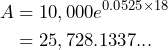
Therefore, there will be $25,728.13 in the account when Bennett turns 18.
- What age would Bennett be to have $30,000 in the account?
Solution
We know that ![]() and
and ![]() , so the equation is:
, so the equation is:
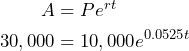
To solve the equation for ![]() , we can start by dividing both sides by 10,000 to simplify:
, we can start by dividing both sides by 10,000 to simplify:
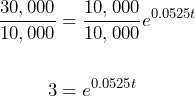
Now we have an equation in the form ![]() , which can be written in its equivalent logarithmic form
, which can be written in its equivalent logarithmic form ![]() :
:
![]()
To solve for ![]() we must divide both sides of the equation by 0.0525, and we can write
we must divide both sides of the equation by 0.0525, and we can write ![]() as
as ![]() :
:
![]()
Finally, using a calculator, ![]()
Bennett will be almost 21 when there is $30,000 in the account.
- What would the interest rate have to be for there to be $30,000 in the account when Bennett turns 18?
Solution
This time we have ![]() so the equation is:
so the equation is:
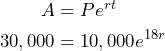
To solve the equation for ![]() , we can start by dividing both sides by 10,000 to simplify:
, we can start by dividing both sides by 10,000 to simplify:
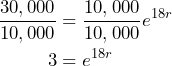
Now we have an equation in the form ![]() , which can be written in its equivalent logarithmic form
, which can be written in its equivalent logarithmic form ![]() :
:
![]()
To solve for ![]() we must divide both sides of the equation by 18. We must also write
we must divide both sides of the equation by 18. We must also write ![]() as
as ![]() :
:
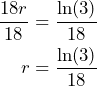
Finally, using a calculator we get:
![]()
The interest rate would have to be 6.103%.
Explore 5 – Logarithms base 2
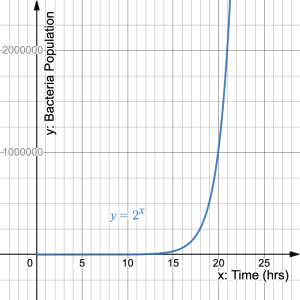
The graph represents the population of bacteria in a petri dish over time. The exponential equation is ![]() .
.
- How long will it take to reach 32 bacteria?
Solution
Determining the point on the graph where ![]() is practically impossible due to the scale on the
is practically impossible due to the scale on the ![]() -axis.
-axis.
If we use the equation, we substitute ![]() into the equation and solve for
into the equation and solve for ![]() :
:
![]()
The question we need to answer is, 2 to what power equals 32? The pattern for the powers of 2 is: ![]() . Since,
. Since, ![]() , the exponent must be 5. So, the solution of the equation
, the exponent must be 5. So, the solution of the equation ![]() is
is ![]() . This means that is takes 5 hours to reach 32 bacteria.
. This means that is takes 5 hours to reach 32 bacteria.
We could also write the exponential equation as an equivalent logarithm to determine the solution:
![]()
The base of the logarithm is identical to the base of the exponential equation: 2
The exponent is identical to the logarithm of the value: ![]()
Since ![]() ,
, ![]() must equal 5. This is because if
must equal 5. This is because if ![]() then
then ![]() .
.
- How long will it take to reach 2,000,000 bacteria?
Solution
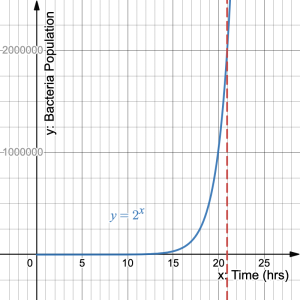
If we use the graph, we can drop a vertical line from where the graph has a ![]() -value of 2,000,000. It is difficult to see exactly where the vertical line crosses the
-value of 2,000,000. It is difficult to see exactly where the vertical line crosses the ![]() -axis, but it looks to be just shy of 21 hours. Unfortunately, 2,000,000 is not a whole number power of 2. For example,
-axis, but it looks to be just shy of 21 hours. Unfortunately, 2,000,000 is not a whole number power of 2. For example, ![]() and
and ![]() .
.
This tells us that:
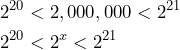
which means that since all of the bases are the same (i.e., 2), the exponent ![]() must be a value between 20 and 21:
must be a value between 20 and 21:
![]()
If we use the equation, we substitute ![]() into the equation and solve for
into the equation and solve for ![]() :
:
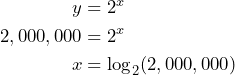
But how do we evaluate ![]() ?
?
Continued below
 The Change of Base Formula
The Change of Base Formula
There are only two logarithm buttons with base 10 and ![]() on a scientific calculator, so how do we evaluate a logarithm whose base is neither 10 nor
on a scientific calculator, so how do we evaluate a logarithm whose base is neither 10 nor ![]() when the argument is not a perfect power of the base? To solve the problem, we may use the change of base formula. The formula says you may change any logarithm into the quotient of two logarithms with the same base, and you may choose any base you want. Naturally, to evaluate a logarithm we want to use a base whose logarithms are already known: base 10 or base
when the argument is not a perfect power of the base? To solve the problem, we may use the change of base formula. The formula says you may change any logarithm into the quotient of two logarithms with the same base, and you may choose any base you want. Naturally, to evaluate a logarithm we want to use a base whose logarithms are already known: base 10 or base ![]() .
.
The Change of Base Formula
For all ![]() ,
, ![]()
For example, to find ![]() , we use the change of base formula,
, we use the change of base formula, ![]() using common logarithms, or
using common logarithms, or ![]() using natural logarithms. Either way,
using natural logarithms. Either way, ![]() .
.
Explore 5 continued
So it takes about 20.9 hours to reach 2,000,000 bacteria.
Explore 6 – Change of base
The population of an endangered species decreases 5% per year. The current population is 5000. How long will it take for the population to decrease to 100?
Solution
First we write an exponential equation that represents the population ![]() at any time
at any time ![]() . The initial value is 5000 and the rate of change is –5% per year (the rate of change is negative because the rate is decreasing). This means that the constant ratio is 1 – 0.05 = 0.95
. The initial value is 5000 and the rate of change is –5% per year (the rate of change is negative because the rate is decreasing). This means that the constant ratio is 1 – 0.05 = 0.95
Therefore, the exponential equation is: ![]() .
.
Now we can substitute ![]() into the equation and solve for
into the equation and solve for ![]() :
:
![]()
To be able to convert the exponential equation to an equivalent logarithmic equation, we must get the equation into the form ![]() . We achieve this by dividing both sides by 5000. Then we can write an equivalent logarithmic equation and use the change of base formula to evaluate the logarithm:
. We achieve this by dividing both sides by 5000. Then we can write an equivalent logarithmic equation and use the change of base formula to evaluate the logarithm:
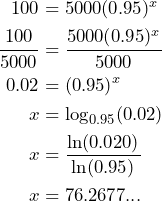
Consequently, it will take a little over 76 years for the population to decrease to 100.

- Under what situations would you use the change of base formula? Why? Explain your reasoning.
Show/Hide Answer
The change of base formula may be used when evaluating a logarithm whose base is not 10 or e. We use the formula because a scientific calculator generally has only two logarithm buttons; common logarithms ![]() with base 10 and natural logarithms
with base 10 and natural logarithms ![]() with base
with base ![]() . Therefore, we may use the change of base property to evaluate a logarithm whose base is neither 10 nor e, using the division of two logarithms where we can choose 10 or
. Therefore, we may use the change of base property to evaluate a logarithm whose base is neither 10 nor e, using the division of two logarithms where we can choose 10 or ![]() as the base for the two logarithms.
as the base for the two logarithms.
Explore 7 – Compound interest
Ray deposited 10,000 into a bank with monthly compound interest gained at 0.75% each month. How long will it take for the account balance to reach $10,500? The monthly increase of 0.75% is an exponential growth. The account balance after ![]() months will be
months will be ![]() . To determine how long it will take the balance to reach $10,500, we set
. To determine how long it will take the balance to reach $10,500, we set ![]() , and then solve the equation for
, and then solve the equation for ![]() (i.e., determine the value of the exponent
(i.e., determine the value of the exponent ![]() ).
).
- What would be your first step in solving the equation
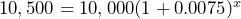 ? Explain your reasoning.
? Explain your reasoning.
Solution
Simplify the equation by adding 1 + 0.0075: ![]() This sets the base of the exponential expression on the right side of the equation.
This sets the base of the exponential expression on the right side of the equation.
- How would you further simplify the equation? Explain your reasoning.
Solution
Divide both sides of the equation by 10,000: ![]() This gets the equation into the form
This gets the equation into the form ![]() , which can now be turned into an equivalent logarithmic equation.
, which can now be turned into an equivalent logarithmic equation.
- How would you solve for
 using a logarithm. Explain your reasoning.
using a logarithm. Explain your reasoning.
Solution
Write an equivalent logarithmic equation: ![]()
- Will you need to use the change of base formula? Explain your reasoning.
Solution
Yes, since only base 10 and base ![]() are embedded in a scientific calculator.
are embedded in a scientific calculator.
- How many months will it take for the account balance to reach $10,500?
Solution
Using the change of base formula:
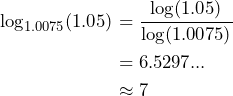 .
.
Since the interest is calculated monthly, we need to round up to 7. So it will take 7 months to have a balance of $10,500.

When calculating a logarithm using the change of base formula, do not write down the numerator and denominator separately then divide the two numbers. This can bring in rounding error. Rather complete the entire calculation using your calculator.
For example to evaluate ![]() , the calculator input will be:
, the calculator input will be:
![]()

- How do we solve for the exponent of an exponential equation
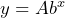 when the initial value
when the initial value 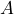 is not 1?
is not 1?
Show/Hide Answer
We divide both sides of the equation by the initial value ![]() so that the equation is turned into an exponential equation with only the base, the result, and the exponent:
so that the equation is turned into an exponential equation with only the base, the result, and the exponent: ![]() . Then, we write the exponential equation as an equivalent logarithmic equation to determine the value of the unknown exponent
. Then, we write the exponential equation as an equivalent logarithmic equation to determine the value of the unknown exponent ![]() .
.
Practice Exercises
- The World population
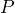 in billions,
in billions, 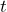 years after 1950, can be represented by the equation
years after 1950, can be represented by the equation 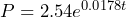 . a) What was the population in 1950? b) What was the population in 2000? c) When did the population reach 8 billion? d) How accurate is this model compared to actual figures?
. a) What was the population in 1950? b) What was the population in 2000? c) When did the population reach 8 billion? d) How accurate is this model compared to actual figures? - A 500ml puddle of water is evaporating at 15% per hour. a) Define variables and write an equation that represents this scenario. b) How much water is left after 4 hours? c) How long will it take for the puddle to be reduced to 1ml?
- A diamond ring was bought a number of years ago for $500. The value of the ring increases by 8% every year. a) Define variables and write an equation that represents this scenario. b) How long does it take for the ring to double in value?
Show/Hide Answer
- a) 2.54 billion b) 6.19 billion c) In 2014 d) Using an Internet search the initial value is correct in 1950 at 2.54 billion; the population in 2000 was 7.84 billion (not 6.19 billion); and the population reached 8 billion in 2023 (not 2014).
- a) Let
 = the size of the puddle in ml, and
= the size of the puddle in ml, and  represent time in hours:
represent time in hours: 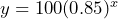 b) 52.2ml c) 28.3 hours
b) 52.2ml c) 28.3 hours - a) Let
 = the value of the ring in dollars, and
= the value of the ring in dollars, and  represent time in years since the ring was bought:
represent time in years since the ring was bought: 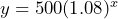 b) just over 9 years
b) just over 9 years
 In this section, we will take what we have learned and apply the concepts to new situations.
In this section, we will take what we have learned and apply the concepts to new situations.
- The acidity or alkalinity of a substance is found using the formula
![Rendered by QuickLaTeX.com pH=-\log[H^+]](https://uen.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-c73034f9edead315f92f78ab5d33e61f_l3.png) where
where 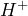 is the hydrogen ion concentration, measured in moles per liter. Solutions with a pH less than 7 are acidic, while solutions with a pH greater than 7 are alkaline. Solutions with a pH of 7 are considered neutral. a) Apple juice is found to have a hydrogen ion concentration of 0.0003 moles per liter. Calculate the pH of apple juice and determine if it is acidic or alkaline. b) Ammonia is found to have a hydrogen ion concentration of
is the hydrogen ion concentration, measured in moles per liter. Solutions with a pH less than 7 are acidic, while solutions with a pH greater than 7 are alkaline. Solutions with a pH of 7 are considered neutral. a) Apple juice is found to have a hydrogen ion concentration of 0.0003 moles per liter. Calculate the pH of apple juice and determine if it is acidic or alkaline. b) Ammonia is found to have a hydrogen ion concentration of 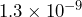 moles per liter. Calculate the pH of ammonia and determine if it is acidic or alkaline.
moles per liter. Calculate the pH of ammonia and determine if it is acidic or alkaline. - The otter population on an island increases by 16% per year. a) Define variables and write an equation that represents this scenario. b)How many years will it take the current population to double?
- The mass
 in grams of a radioactive sample after
in grams of a radioactive sample after  years is represented by the equation
years is represented by the equation 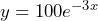 . a) What is the initial mass of the sample? b) How long will it take the sample to reach half of its initial mass? (This time is called the half-life of the radioactive substance)
. a) What is the initial mass of the sample? b) How long will it take the sample to reach half of its initial mass? (This time is called the half-life of the radioactive substance) - A hospital patient is given a 300mg dose of a drug. Each hour, the amount of drug in the patient’s body decreases by 12%. a) Define variables and write an equation that represents this scenario. b) When there is less than 50mg of the drug left in the patient’s body, it is safe to give them another dose. How long will it be before the patient can be given another dose?
- A new car cost $34,760 but its value decreases at 11.5% per year. a) Define variables and write an equation that represents this scenario. b) What is the value of a 3 year old car? c) How long will it take for the value of the car to drop below $20,000?
- A tractor tyre has a slow puncture and is losing pressure at a rate of 5% every hour. The farmer inflates the tyre to 50 psi first thing in the morning. a) Define variables and write an equation that represents this scenario. b) What will the tyre pressure be after 3 hours? c) The tractor can be used safely as long as the pressure stays above 30 psi. How long can the tractor be used before it becomes unsafe?
- The efficiency of a machine drops by 5% each year. When the efficiency drops below 75%, the machine needs to be serviced. a) Define variables and write an equation that represents this scenario. b) After how many years will the machine need to be serviced?
- A town library is expanding its book collection by 2% every year. There are currently 45,630 books on the shelves. a) a) Define variables and write an equation that represents this scenario. b) How long will it take the library to have a collection in excess of 75,000 books?
Show/Hide Answer
- a) pH = 3.522… acidic. b) pH = 8.886… alkaline
- a) Let
 = otter population,
= otter population,  = the initial otter population, and
= the initial otter population, and  = the time passed in years:
= the time passed in years: 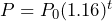 b) 5 years
b) 5 years - a) 100g b) about 0.231 years or 84.315 days
- a) Let
 = amount of drug still in the body and
= amount of drug still in the body and 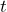 represent the number of hours passed since they were given the drug.
represent the number of hours passed since they were given the drug. 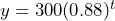 b) 14 hours after the last dose
b) 14 hours after the last dose - a) Let
 = value of the car in dollars and
= value of the car in dollars and  = the age of the car in years:
= the age of the car in years: 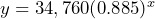 . b) $24,094. c) about 4.5 years
. b) $24,094. c) about 4.5 years - Let
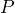 = tyre pressure in psi and
= tyre pressure in psi and 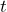 = the time after the tyre has been inflated:
= the time after the tyre has been inflated: 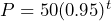 . b) 42.9 psi c) 9.5 hours
. b) 42.9 psi c) 9.5 hours - a) Let
 = efficiency of the machine and
= efficiency of the machine and  = the time passed in years:
= the time passed in years: 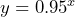 b) 5.6 years
b) 5.6 years - a) Let
 = number of books and
= number of books and  = the time passed in years:
= the time passed in years: 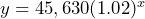 b) 26 years
b) 26 years
 In this section, we will use what we have learned so far to practice skill problems.
In this section, we will use what we have learned so far to practice skill problems.
Solve for ![]() :
:
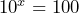 .
.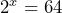 .
.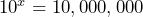 .
.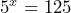 .
.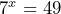 .
.
Write the equation in equivalent exponential form and solve for ![]() :
:
Evaluate the logarithm. Round to 4 decimal places if necessary:
Solve the equation for ![]() . Round to 4 decimal places if necessary:
. Round to 4 decimal places if necessary:
Solution
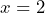
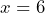
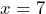
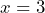
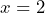
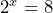 ,
, 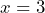
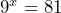 ,
, 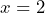
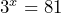 ,
, 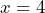
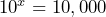 ,
, 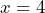
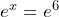 ,
, 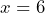
- 4
- 2
- 1.7227
- 1
- 2
- 1.5283
- 2.4849
- 1.6309
- 0
- 0
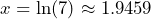
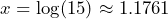
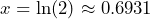
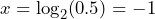
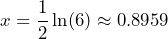
The set of numbers that cannot be written as fractions using whole numbers.