CHAPTER 7: EXPONENTIAL AND LOGARITHMIC GROWTH
7-4: Exponential Growth and Decay
Introduction
The word growth implies that a quantity is increasing in value, while decay implies that a quantity is decreasing in value. An exponential equation of the form ![]() can show growth or decay. It all depends on the value of the constant ratio
can show growth or decay. It all depends on the value of the constant ratio ![]() .
.
 Exponential Growth & Decay
Exponential Growth & Decay
Unlike linear growth that increases or decreases by adding or subtracting a constant multiple times to an initial value, exponential growth (or decay) increases or decreases by multiplying the initial value over and over by a constant ratio.
Explore 1 – Exponential growth
Suppose that a single bacterium is placed in a petri dish and the number of bacteria doubles every hour. The growth of the bacteria is illustrated in the table.
| Time (hours) | 0 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|---|
| Population | 1 | 2 | 4 | 8 | 16 | 32 |
- What is the initial value and constant ratio?
Solution
The initial value occurs at hour 0, so it is 1 bacterium. The bacteria doubles every hour, so the constant ratio is 2.
- Define variables and write an equation to represent the number of bacteria in terms of the number of hours. Express the units of the variables. Explain your reasoning.
Solution
Let ![]() represent the number of bacteria and
represent the number of bacteria and ![]() represent the number of hours, then the equation is
represent the number of hours, then the equation is ![]() or simply
or simply ![]()
- Use the equation to determine the number of bacteria in the petri dish after 24 hours.
Solution
We substitute ![]() into the equation:
into the equation: ![]() , so in 24 hours there will be 16,777,216 bacteria.
, so in 24 hours there will be 16,777,216 bacteria.
- Use desmos to draw a graph representing the equation, then describe the graph.
Solution
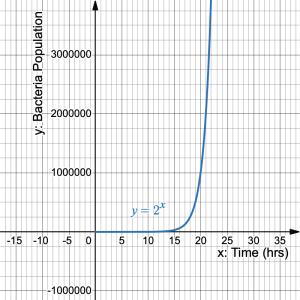
The graph is continuously increasing, slowly at first then very quickly.
- Use the graph to determine the time it takes to exceed 2,000,000 bacteria.
Solution
About 21 hours.
The equation and graph in Explore 1 with a constant ratio of 2 are examples of exponential growth. However, just like with linear patterns, the values can decrease rather than increase. In the next Explore we illustrate exponential decay.
Explore 2 –Exponential decay
 At Halloween, Calum dressed up and went trick or treating for candy. At the end of the night he had 160 pieces of candy. He reasoned that if he ate half of his stash every week, he would never run out of candy.
At Halloween, Calum dressed up and went trick or treating for candy. At the end of the night he had 160 pieces of candy. He reasoned that if he ate half of his stash every week, he would never run out of candy.
- What is the initial value and what is the constant ratio?
Solution
The initial value is the number of pieces of candy Calum started with at week 0: 160 pieces of candy. Since he eats half of the candy each week, 1/2 the number of pieces of candy remain so the constant ratio is ![]() or 0.5.
or 0.5.
- Define the variables and write an equation that represents the amount of candy over time.
Solution
Let ![]() = the number of weeks since Halloween and
= the number of weeks since Halloween and ![]() = the number of pieces of candy, then
= the number of pieces of candy, then ![]()
- Use desmos to graph the equation
Solution
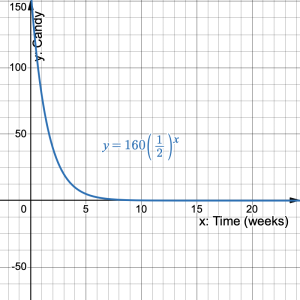
- Where on the graph is the initial value? What do you notice about the graph?
Solution
The initial value of 160 is at the ![]() -intercept (0, 160). The graph is continuously decreasing, but never crosses the
-intercept (0, 160). The graph is continuously decreasing, but never crosses the ![]() -axis.
-axis.
- Use the graph to determine if the number of pieces of candy ever reaches zero? Explain your reasoning.
Solution
No. The graph never crosses the ![]() -axis, so
-axis, so ![]() is always positive and never reaches zero. No matter what fraction of a single piece of candy is left it can always (mathematically) be halved.
is always positive and never reaches zero. No matter what fraction of a single piece of candy is left it can always (mathematically) be halved.
A fundamental feature of an exponential decay graph is that its values get smaller and smaller but never quite reach zero. In mathematics, we say that the graph has an asymptote at ![]() , the
, the ![]() -axis. In other words, the
-axis. In other words, the ![]() -values get closer and closer to zero but never quite make it, no matter how large the
-values get closer and closer to zero but never quite make it, no matter how large the ![]() -value gets.
-value gets.
 In the exponential equation
In the exponential equation ![]() , what values of
, what values of ![]() indicate growth and what values indicate decay?
indicate growth and what values indicate decay?
Show/Hide Answer
When ![]() the equation indicates growth since multiplying by the constant ratio increases the previous value.
the equation indicates growth since multiplying by the constant ratio increases the previous value.
When ![]() (i.e., is a positive proper fraction) the equation indicates decay since multiplying by the constant ratio decreases the previous value.
(i.e., is a positive proper fraction) the equation indicates decay since multiplying by the constant ratio decreases the previous value.
Example
A Youtube video goes viral. The number of views triples each hour starting with 5 people.
- What is the initial value and the constant ratio?
- Define variables and write an equation to represent the number of views in terms of the number of hours.
- Use Desmos.com to graph the equation.
- Use the graph to determine how long it takes to get 1,000,000 views.
Solutions
- The initial value is 5 views. The constant ratio is 3. Every hour the number of views gets multiplied by 3.
- Let
 = the number of hours and
= the number of hours and  = the number of views. Then the equation is
= the number of views. Then the equation is 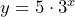 because the initial number of views 5 is multiplied by 3,
because the initial number of views 5 is multiplied by 3,  times.
times. 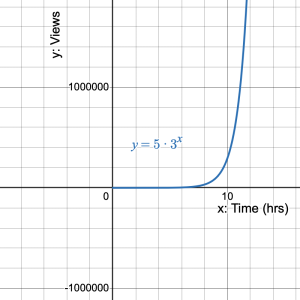
- A little over 11 hours.
Exponential Growth and Decay
The standard form of an exponential equation is ![]() where
where ![]() is the initial value and
is the initial value and ![]() is the constant ratio.
is the constant ratio.
When ![]() there is exponential growth and when
there is exponential growth and when ![]() there is exponential decay.
there is exponential decay.
The graph of exponential growth is a continuous graph that is always increasing. The graph of exponential decay is a continuous graph that is always decreasing but never reaches zero.
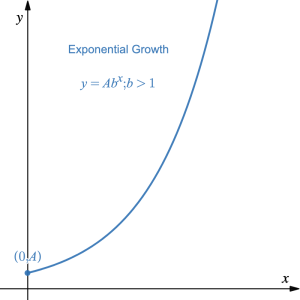
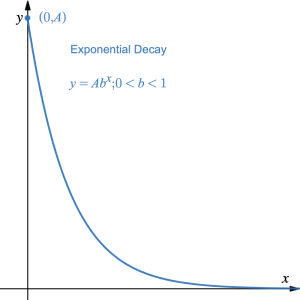

- The standard form of an exponential equation is
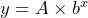 . What do the
. What do the 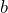 and
and  represent? Explain your reasoning.
represent? Explain your reasoning.
Show/Hide Answer
The variable ![]() represents the constant ratio that is repeatedly multiplied onto the initial value
represents the constant ratio that is repeatedly multiplied onto the initial value ![]() in an exponential growth pattern.
in an exponential growth pattern. ![]() is the constant ratio
is the constant ratio ![]() of two adjacent
of two adjacent ![]() -values,
-values, ![]() . The variable
. The variable ![]() represents the number of times the constant is multiplied.
represents the number of times the constant is multiplied.
 Growth and Decay Rates in Exponential Equations
Growth and Decay Rates in Exponential Equations
The constant ratio in exponential growth and decay tells us the number that gets repeatedly multiplied onto an initial value. If the constant ratio is 2, then each ![]() value doubles for every increase of 1 of the
value doubles for every increase of 1 of the ![]() -value. For example, with an initial value of 3 and a constant ratio of 2, the equation
-value. For example, with an initial value of 3 and a constant ratio of 2, the equation ![]() represents the exponential growth, and the growth pattern is 3, 6, 12, 24, 48, 96, … Notice that when the constant ratio is 2, the percent increase is 100% (i.e., Percent increase = (6 – 3)/3 = 1 = 100%). The percent increase is known as the growth rate in an exponential equation. Likewise, if the constant ratio,
represents the exponential growth, and the growth pattern is 3, 6, 12, 24, 48, 96, … Notice that when the constant ratio is 2, the percent increase is 100% (i.e., Percent increase = (6 – 3)/3 = 1 = 100%). The percent increase is known as the growth rate in an exponential equation. Likewise, if the constant ratio, ![]() lies between 0 and 1, the percent decrease is known as the decay rate in an exponential equation.
lies between 0 and 1, the percent decrease is known as the decay rate in an exponential equation.
Explore 3 – Growth rate as percent increase
The population of a small town increases by 50% every year due to the opening of a nearby ski resort. Suppose the initial population is 170.
- What is the growth rate?
Solution
The growth rate is 50%
- What is the constant ratio? Explain your reasoning.
Solution
A growth rate of 50% means that any initial value ![]() increases to
increases to ![]() (i.e., 100% of the population + 50% growth = 150% of the population = 1.5 times the population). This means that the constant ratio is 1.5.
(i.e., 100% of the population + 50% growth = 150% of the population = 1.5 times the population). This means that the constant ratio is 1.5.
- What is the relationship between the growth rate and the constant ratio? .
Solution
The constant ratio = 1 + the growth rate or the growth rate = the constant ratio – 1
- Define variables then write an equation that represents the population over time.
Solution
Let ![]() = the population of the town and
= the population of the town and ![]() = the number of years since the ski resort opened, then
= the number of years since the ski resort opened, then ![]()
- What is the population of the small town after 5 years?SolutionAfter 5 years means
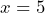 , or
, or 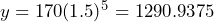 . The population of the town after five years will be 1290 people.
. The population of the town after five years will be 1290 people.
- Do you think the population will keep increasing by 50% forever? Explain your reasoning
Solution
No. People will die or move out of the town, plus every town has a limited population due to space.
Explore 4 – Percent increase as the growth rate
Emily invests $5000 in an account with a monthly compound interest growth rate of 1.6%. The account balance is multiplied by 1.016 (e.g., 1+1.6%=1+0.016=1.016) per month. Suppose the initial deposit is $5,000.
- What is the constant ratio?
Solution
The constant ratio = 1 + growth rate = 1 + 1.6% = 1 + 0.016 = 1.016
- Write an equation that represents the amount of money in the account over time.
Solution
Let ![]() = time (in months) and
= time (in months) and ![]() =the amount in the account (in dollars), then
=the amount in the account (in dollars), then ![]()
- What is the account balance after 5 years?SolutionFive years is equal to 60 months (i.e.,
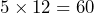 ). After five years means
). After five years means 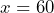 , or
, or 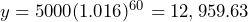 . Therefore, the account balance will be $12,959.63 after 5 years.
. Therefore, the account balance will be $12,959.63 after 5 years. - Graph the equation and determine how long it will take to double the initial deposit.
Solution
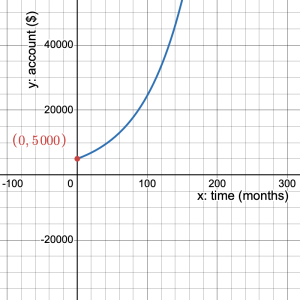
When ![]() , the
, the ![]() -value of just under 44. This means it will take 44 months for the initial deposit to double since interest is accumulated only once per month.
-value of just under 44. This means it will take 44 months for the initial deposit to double since interest is accumulated only once per month.
Explore 5 – Percent decrease as the decay rate
The population of a small town decreases by 5% each year. Suppose the town has an initial population of 10,000.
- What is the decay rate?
Solution
The decay rate is 5%
- What is the constant ratio? Explain your reasoning.
Solution
A decay rate of 5% means that any initial value ![]() decreases to
decreases to ![]() (i.e., 100% of the population – 5% decay = 95% of the population = 0.95 times the population). This means that the constant ratio is 0.95.
(i.e., 100% of the population – 5% decay = 95% of the population = 0.95 times the population). This means that the constant ratio is 0.95.
- Write an equation that represents the population over time.
Solution
Let ![]() = time (in years) and
= time (in years) and ![]() = the population, then
= the population, then ![]()
- What is the population of the town after 10 years? How many 0.95s are multiplied after 10 years? Explain your reasoning.
Solution
We substitute ![]() into the equation:
into the equation: ![]() The population will be 5987 after 10 years.
The population will be 5987 after 10 years.
- Graph the equation using Desmos.com
Solution
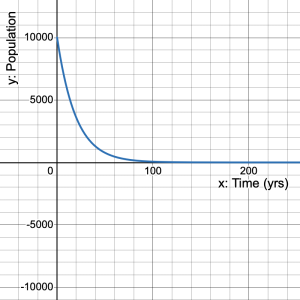
- According to the graph, how long will it take for the population to reach zero?
Solution
Since the graph never reaches the ![]() -axis, the population will never reach zero. However, since we can’t have a fraction of a person, moving the red dot till we get to the last person will take about 179 years.
-axis, the population will never reach zero. However, since we can’t have a fraction of a person, moving the red dot till we get to the last person will take about 179 years.
Exponential Equations
The standard form of an exponential equation is ![]() , where
, where ![]() = the initial value and
= the initial value and ![]() = the constant ratio.
= the constant ratio.
When ![]() , the equation represents exponential growth. When
, the equation represents exponential growth. When ![]() , the equation represents exponential decay.
, the equation represents exponential decay.
The rate of change can be used to write exponential equation ![]() , where
, where ![]() is the rate of change.
is the rate of change.
When ![]() , the rate of change is a growth rate. When
, the rate of change is a growth rate. When ![]() , the rate of change is a decay rate.
, the rate of change is a decay rate.
The relationship between the constant ratio and the rate of change is ![]()
Example
An upcoming politician claims that, “the war in Ukraine cured COVID-19,” implying that the moment the war in Ukraine began, the coverage and discussion about COVID-19 significantly declined. We can model the frequency of news reports on COVID-19 using the exponential equation ![]() , where
, where ![]() represents the number of news reports, and
represents the number of news reports, and ![]() is the number of days since the outbreak of the war.
is the number of days since the outbreak of the war.
- a) What is the initial number of news reports about COVID-19?
- b) What is the growth rate, and how does it relate to the context of the question?
- c) What is the number of news reports after 60 days?
Show/Hide Answer
- a) The initial number of news reports about COVID-19 before the war started was 100.
- b) In the equation
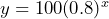 , the constant ratio is 0.8. This means that the growth rate is (0.8 – 1) = –0.2 = –20%. In the context of the question, this rate represents the rate at which the number of news reports on COVID-19 decreases each day after the war began. Since the constant ratio of 0.8 is less than 1, it indicates exponential decay, meaning that the coverage of COVID-19 decreases by 20% each day as the media’s focus shifts to the war in Ukraine.
, the constant ratio is 0.8. This means that the growth rate is (0.8 – 1) = –0.2 = –20%. In the context of the question, this rate represents the rate at which the number of news reports on COVID-19 decreases each day after the war began. Since the constant ratio of 0.8 is less than 1, it indicates exponential decay, meaning that the coverage of COVID-19 decreases by 20% each day as the media’s focus shifts to the war in Ukraine. - c) To find the number of news reports,
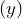 , after 60 days,
, after 60 days, 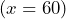 , we can substitute
, we can substitute 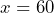 into the equation:
into the equation: 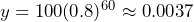 Therefore, after 60 days since the war began, there would be approximately 0.0037 news reports about COVID-19. This illustrates the significant decline in media coverage on the pandemic as the attention shifts to the ongoing war in Ukraine.
Therefore, after 60 days since the war began, there would be approximately 0.0037 news reports about COVID-19. This illustrates the significant decline in media coverage on the pandemic as the attention shifts to the ongoing war in Ukraine.

- The standard form of an exponential equation
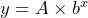 may be rewritten as
may be rewritten as 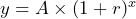 from the perspective of the growth rate and
from the perspective of the growth rate and 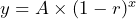 from the perspective of the decay rate (negative growth rate). What is the difference between the two equations?
from the perspective of the decay rate (negative growth rate). What is the difference between the two equations?
Show/Hide Answer
The difference is that the ![]() in the growth-rate form is a percent change that gets added to the original 100% to get
in the growth-rate form is a percent change that gets added to the original 100% to get ![]() , while the
, while the ![]() in the standard form is the constant ratio that gets multiplied a number of times onto the initial value. Indeed,
in the standard form is the constant ratio that gets multiplied a number of times onto the initial value. Indeed, ![]() . For example, if a population increases each year by 40%, then
. For example, if a population increases each year by 40%, then ![]() , so
, so ![]() . But a 40% increase each year is equivalent to multiplying by a constant ratio of
. But a 40% increase each year is equivalent to multiplying by a constant ratio of ![]() since the new population will be 140% = 1.4 of the previous population. Likewise, the decay rate gets subtracted from 1 to get the constant ratio (i.e.,
since the new population will be 140% = 1.4 of the previous population. Likewise, the decay rate gets subtracted from 1 to get the constant ratio (i.e., ![]() ). A decay rate is equivalent to a negative growth rate.
). A decay rate is equivalent to a negative growth rate.
Practice Exercises
- The value of a car depreciates by a constant rate of 35% for the cycle of every 25,000 miles driven. a) If the original cost of the car was $56,450, define variables and write an equation that represents the value of the car according to its mileage. b) What is the value of the car to the nearest dollar when it’s mileage is 75,000 miles? c) What is the value of the car to the nearest dollar whose mileage is 150,000 miles. d) Graph your equation and estimate when the car becomes worthless.
- Fiona inherits $40,000 from the estate of her late uncle. She invests the funds into an account that pays compound interest once per year. The table shows the balance in the account after 0 – 5 years.
Time (years) 0 1 2 3 4 5 Balance ($) 40,000 42,080 44,268.16 46,570.10 48,991.75 51,539.32 a) What is the constant ratio? b) What is the interest rate on the account? c) Use reasoning to determine the balance of the account after 6 years. d) Define variables and write an equation that represents the balance of the account over time. e) What will be the balance of the account after 12 years? f) Use Desmos to graph your equation. g) How long will it take to have a balance of $90,000?
Show/Hide Answer
- a) Let
 = the number of cycles of the car’s mileage in 25,000 mile and
= the number of cycles of the car’s mileage in 25,000 mile and  = the value of the car in dollars.
= the value of the car in dollars. 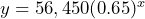 b) $15,503 c) $4257 d)
b) $15,503 c) $4257 d) 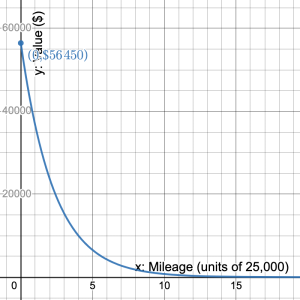 Although the graph never reaches zero, the car becomes basically worthless around 14 units = 14(25,000 miles) = 350,000 miles.
Although the graph never reaches zero, the car becomes basically worthless around 14 units = 14(25,000 miles) = 350,000 miles. - a) 1.052 b) 5.2% c) $54,219.36 d) Let
 = time in years and
= time in years and  = account balance in dollars, then
= account balance in dollars, then 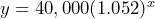 e) $73,493.49 f)
e) $73,493.49 f)  g) about 16 years
g) about 16 years
 In this section, we will take what we have learned and apply the concepts to new situations.
In this section, we will take what we have learned and apply the concepts to new situations.
Perspectives
- Wounds and bruises take time to heal properly. Interestingly, the healing of wounds and bruises depends on the concept of exponential decay because the size of the wound, during the process of healing, is reduced consistently at a constant rate. This means that if the rate of healing of the wound is known, the time when the wound would get properly healed can be estimated accurately. Suppose a wound has an initial size of 4.5mm. The size decreases at a rate of 7.5% per day. a) Define variables and write an exponential equation that represents the size of the wound over time. b) What will be the size of the wound after 3 days? c) What will be the size of the wound after 2 weeks? d) Use desmos to graph your equation and determine how long it will take for the wound to heal completely.
- Forest fires burn at an exponential rate, quickly devouring everything in their path. When a forest ranger first spied a forest fire from a fire tower it had burned 1.5km2. After 1 hour, the fire had burned 3.6 km2. a) What is the constant ratio? b) What is the growth rate? c) Define variables and write an exponential equation that represents the area burned by the fire over time. d) If it takes a fire crew 8 hours to reach the area where the fire is burning, what area will have already burned? e) If fire crews establish a perimeter to control the fire after 110 hours, what area will have already burned? f) Use desmos to graph your equation. g) How long will it take for the fire to grow to 55,000km2 burned?
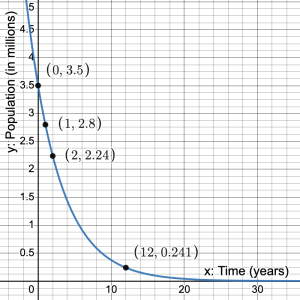 The graph shows the decline in population of a bird species with
The graph shows the decline in population of a bird species with 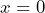 representing 2010.
representing 2010.
a) What is the initial value? b) Determine the constant ratio. c) What is the rate and what does it represent? d) Define variables and write an equation to represent the population over time. e) What will the population be in 2030? f) If the trend continues, when will the population reach 500,000? g) What does a negative value of ![]() represent? h) What was the population in 1990?
represent? h) What was the population in 1990?
- The state of Utah has experienced an annual 1.5% population growth since 1990. In 1990, there were 1.7 million residents. The population of Utah in millions can be modeled by the equation
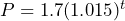 where
where 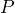 is the population in millions and
is the population in millions and 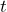 is the number of years since 1990. a) Identify the initial value and explain what it represents. b) Identify the growth rate and explain what it represents. c) According to the model, what was the population in 2020? d) According to the model, what is the expected population in 2050? What assumption is being made?
is the number of years since 1990. a) Identify the initial value and explain what it represents. b) Identify the growth rate and explain what it represents. c) According to the model, what was the population in 2020? d) According to the model, what is the expected population in 2050? What assumption is being made?
- A farmer introduces 6 rabbits to his barn. The rabbits populate the barn at an exponential rate of 150% per year. a) What is the initial value? b) What is the constant ratio? c) Define variables and write an equation representing the population of rabbits in the barn over time. d) How many rabbits will there be after 1 year? e) How many rabbits will there be after 5 years? f) How many rabbits will there be after 18 months?
- According to the National Institute of Health, poor communities have higher COVID-19 infection rates compared to the middle- and upper-class communities. In Utah, Piute County has a larger number of poor communities than Summit County. Suppose we can model Piute County’s infection rates using the exponential equation
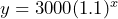 , and Summit County’s infection rates using the exponential equation
, and Summit County’s infection rates using the exponential equation 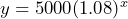 . a) What are the initial infections in Piute and Summit counties? b) Which county has the higher growth rate of infections? c) Which county had more infections after 10 days? d) Why did Summit County have more infections despite having more middle- and upper-class people than Piute County? e) Graph each county’s model on the same set of axes, and comment on the graphs. Does Summit County always have a higher number of cases?
. a) What are the initial infections in Piute and Summit counties? b) Which county has the higher growth rate of infections? c) Which county had more infections after 10 days? d) Why did Summit County have more infections despite having more middle- and upper-class people than Piute County? e) Graph each county’s model on the same set of axes, and comment on the graphs. Does Summit County always have a higher number of cases?
Show/Hide Answer
-
- a) Let
 = the size of the wound in millimeters and
= the size of the wound in millimeters and  = time in days, then
= time in days, then 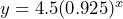 b) 3.56mm c) 1.51mm d)
b) 3.56mm c) 1.51mm d) 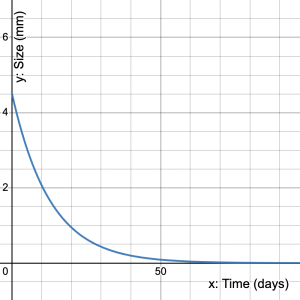 The graph never reaches zero, but the wound will be of negligible size (<0.01mm) after about 80 days.
The graph never reaches zero, but the wound will be of negligible size (<0.01mm) after about 80 days. - a) 2.4 b) 140% c) Let
 = area burned in acres and
= area burned in acres and  = time in hours, then
= time in hours, then 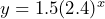 d) 1651km2 e)
d) 1651km2 e) 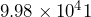 km2 f) 23
km2 f) 23 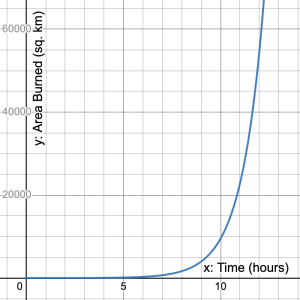 g) Just over 12 hours.
g) Just over 12 hours. - a) 3.5 million or 3,500,000 b) 0.8 c) –20%; The population decreases by 20% every year d) Let
 = time since 2010 and
= time since 2010 and  = bird population, then
= bird population, then 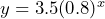 . e) 40,352 f) about two-thirds of the way through 2018 g) 303.58 million
. e) 40,352 f) about two-thirds of the way through 2018 g) 303.58 million - a) 1.7 million; the number of residents of Utah in 1990. b) 1.5%; the population grows by 1.5% every year. c) 2.657 million. d) 4.153 million
- a) 6 rabbits b) 2.5 c) Let
 = the population of rabbits and
= the population of rabbits and  = time in years, then
= time in years, then 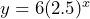 d) 15 e) 585 f) 23
d) 15 e) 585 f) 23 - a) Initial infections in Piute County = 3000; Initial infections in Summit County = 5000 b). For Piute County, the constant ratio is 1.1, so the growth rate is 0.1.; For Summit County, the constant ratio is 1.08, so the growth rate is 0.08. Piute County has the higher rate. c) Piute County: 7781 infections; Summit County 10,795 infections. Summit County had more infections after 10 days. d) Despite having a lower initial growth rate (0.08), Summit County had more infections after 10 days because it started with a significantly higher number of initial infections (5000) compared to Piute County’s initial infections (3000). The higher starting number of infections in Summit County allowed the cumulative number of infections to surpass Piute County’s total after 10 days, despite Piute County having a higher growth rate (0.1). The larger base number of infections in Summit County gave it an advantage in terms of total infections over time. Additionally, the presence of more middle- and upper-class people in Summit County may not have been sufficient to offset the initial difference in infection rates due to other factors such as population density, healthcare infrastructure, and adherence to preventive measures. e)
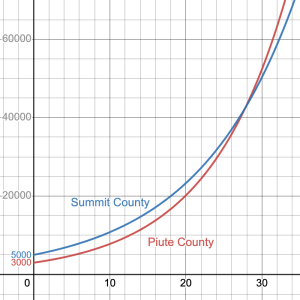 The number of Summit County infections remains greater than the number of Piute County infections until around 28 months (where the graphs cross).
The number of Summit County infections remains greater than the number of Piute County infections until around 28 months (where the graphs cross).
- a) Let
 In this section, we will use what we have learned so far to practice skill problems.
In this section, we will use what we have learned so far to practice skill problems.
Skill Exercises
Given a growth/decay rate, determine the constant ratio in an exponential equation and state whether this represents growth or decay:
- 20%
- 3%
- –7%
- 2.5%
- –6.25%
- –0.5%
Given the constant ratio, determine the growth/decay rate and state whether this represents growth or decay;
- 1.8
- 2.3
- 0.9
- 0.75
- 1.045
- 0.993
Show/Hide Answer
- 1.2 growth
- 1.03 growth
- 0.93 decay
- 1.025 growth
- 0.9275 decay
- 0.995 decay
- 80% growth
- 130% growth
- 10% decay
- 25% decay
- 4.5% growth
- 0.3% decay

