7-2: Exponential Patterns

Hazel McKenna; Leo Chang; Roxanne Brinkerhoff

CHAPTER 7: EXPONENTIAL AND LOGARITHMIC GROWTH

7-2: Exponential Patterns

Introduction

In Chapter 6, we looked at linear patterns and saw that linear patterns are the result of repeatedly adding a constant rate of change to an initial value. The resulting equation, $y=mx+b$ , generated a line in the coordinate plane with a slope equal to the rate of change and a $y$ -intercept representing the initial value. If, instead of adding a constant to an initial value, we repeatedly multiply a constant onto an initial value we will produce an exponential pattern. Exponential patterns occur in nature and are used to solve problems in daily life. Population growth or decline can often be represented by an exponential equation. Compound interest, radioactive decay, bacterial growth, earthquake intensity, carbon dating, chain reactions in chemistry, and so many more examples are all governed by exponential equations.

Exponential Patterns

Unlike linear patterns that change by adding a constant repeatedly to an initial value, exponential patterns change by repeatedly multiplying an initial value by a constant ratio.

Explore 1 – Exponential growth pattern

Suppose that a single bacterium is placed in a petri dish and the number of bacteria doubles every hour. The growth of the bacteria is illustrated in the table.

Hours	Number of Bacteria	Exponential Expression	Base	Exponent
0	1	$2^0$	2	0
1	$1\times2$	$2^1$	2	1
2	$1\times2\times2$	$2^2$	2	2
3
4
…
20
…
$n$
…

Complete the table, paying attention to the pattern.

Solution

Hours

Number of Bacteria

Exponential Expression

Base

Exponent

0

1

$2^0$

2

0

1

$1\times2=2$

$2^1$

2

1

2

$(1\times2)\times2=4$

$2^2$

2

3

$(1\times2\times2)\times2=8$

$2^3$

2

3

4

$(1\times2\times2\times2)\times2=16$

$2^4$

2

4

…

20

$(1\times2^{19})\times2=2^{20}$

$2^{20}$

2

20

…

$n$

$(1\times2^{n-1})\times2=2^n$

$2^n$

2

$n$

…

Explain in words what happens to the number of bacteria for every increase of 1 hour.

Solution

For every increase of 1 hour, the number of bacteria is multiplied by 2. The constant ratio is 2.

Does the column titled Hours correspond with the column titled Exponent? Why? Explain your reasoning.

Solution

Yes. As the exponent increases by 1, the number of bacteria is multiplied by 2. This results in the exponent on the 2 increasing by 1. And since both the hours and the exponent start at 0 (since 2⁰ = 1), the exponent equals the number of hours.

What is the initial value? What is the constant ratio?

Solution

The initial value occurs at hour 0, so it is 1 bacterium. The constant ratio is the number that gets multiplied onto the previous value. It can always be found by looking at the ratio of adjacent values: 2/1 = 2 (or 4/2 = 2, 8/4 = 2 etc.).

Write an expression that represents the number of bacteria present after 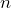$n$ hours

Solution

Following the pattern in the table, the number of bacteria after $n$ hours is $2^n$ .

Graph the data points from the table. What do you notice about the graph?

Graph of plotted points from table

The graph starts at (0, 1) showing the initial value at the $y$ -intercept. The graph curves upwards and is always increasing.

To evaluate an exponential expression using a calculator we use either the carat key $\boxed{\wedge}$ or the exponent key $\boxed{y^x}$ .To evaluate 2²⁴, the input will be $\boxed{2}\;\boxed{\wedge}}\;\boxed{24}\;\boxed{\text{ENTER}}$

Alternatively, the input is $\boxed{2}\;\boxed{y^x}\;\boxed{24}\;\boxed{=}$

Either way, the result is 16,777,216.

Remember that the $\boxed{\text{ENTER}}$ key and the $\boxed{=}$ key are equivalent.

The pattern in Explore 1 with a constant ratio of 2 shows an increasing pattern of values. However, just like with linear patterns, the values can decrease rather than increase.

Explore 2 –Exponential decay pattern

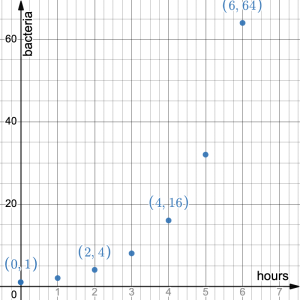
At Halloween, Calum dressed up and went trick or treating for candy. At the end of the night he had 160 pieces of candy. He reasoned that if he ate half of his stash every week, he would never run out of candy.

Complete the table:

Week	0	1	2	3	4	5	6
Pieces of candy	160

Solution

Week	0	1	2	3	4	5	6
Pieces of candy	160	80	40	20	10	5	2.5

Explain in words what happens to the number of pieces of candy for every increase of 1 week.

Solution

Each week half of the candy gets eaten so the number of pieces of candy is divided by 2. This can also be seen as the number of pieces of candy is multiplied by $\frac{1}{2}$ .

What is the initial value and what is the constant ratio?

Solution

The initial value is the number of pieces of candy Calum started with at week 0: 160 pieces of candy.

The constant ratio is the number that gets multiplied onto the previous value. Since the number of pieces of candy is divided by 2, the constant ratio is $\frac{1}{2}$ (i.e., dividing by 2 is equivalent to multiplying by 1/2). The constant ratio can also be found by determining the the ratio between adjacent cells of the dependent values: 80/160 = 1/2 (or 40/80 = 1/2 or 5/10 = 1/2 etc.), so the constant ratio is $\frac{1}{2}$ .

Write an expression that represents how many pieces of candy are left after $n$ months.

Solution

Following the pattern in the table, the number of pieces of candy left after $n$ months is $160\times\left(\dfrac{1}{2}\right)^n$

Use the values in the table to draw a graph. What do you notice about the graph?

Solution

Graph showing plotted points from table. The graph is decreasing, but never reaches zero.

Is Calum’s reasoning of never running out of candy reasonable?

Solution

No. Although mathematically there will always be a fraction of a piece of candy left, that piece will get so small that, practically, he will not be able to eat half of it.

A fundamental feature of a decreasing exponential graph is that its values get smaller and smaller but never quite reach zero. In mathematics, we say that the graph has an asymptote at $y=0$ , the $x$ -axis. In other words, the values get closer and closer to 0 but never quite make it.

Reflect Icon

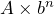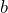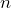An exponential pattern takes the form $A\times b^n$ . What do the $b$ and $n$ represent? Explain your reasoning.

Show/Hide Answer

The variable $b$ represents the constant ratio that is multiplied onto the initial value $A$ each time in an exponential pattern. It is the constant ratio of two adjacent dependent-values. The variable $n$ represents the number of times the constant is multiplied.

Exponential Patterns

An exponential pattern is formed when an initial value is multiplied by a constant ratio.

The constant ratio can never equal 1 nor can it be ≤ 0.

An exponential pattern takes the form $Ab^n$ where $A$ is the initial value and $b$ is the constant ratio.

When $b>1$ the pattern of values is increasing and when $0<b<1$ the pattern of values is decreasing.

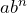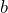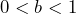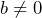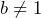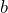In the definition for an exponential pattern $ab^n$ , the value of $b$ must be either greater than 1, or $0<b<1$ . Explain why a) $b\ne0$ b) $b\neq1$ c) $b$ can never be negative.

Show/Hide Answer

a) If 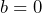$b=0$ , the pattern would be 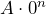$A\cdot0^n$ . Since 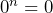$0^n=0$ for all values of 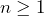$n\ge 1$ the pattern would have values of 0, 0, 0, 0, 0, 0, …, which is a linear pattern with a zero rate of change, not an exponential pattern.

b) If 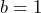$b=1$ , the pattern would be 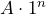$A\cdot 1^n$ . SInce 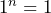$1^n=1$ for all values of 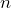$n$ , the pattern would have values of 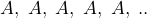$A,\;A,\;A,\;A,\;A,\;..$ , which is a linear pattern with a zero rate of change, not an exponential pattern.

c) If 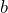$b$ is any negative number, 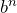$b^n$ will alternate between positive and negative values, which is not an exponential pattern. For example, if 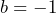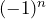$b=-1$ , $(-1)^n$ alternatives between –1 and +1 and the pattern will be 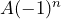$A(-1)^n$ , which has values for 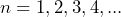$n=1, 2, 3, 4, ...$ of $-A,\;+A,\;-A,\;+A;\,...$ , which is not an exponential pattern.

In this section, we will take what we have learned and apply the concepts to new situations.

Perspectives

Malik started mowing his parent’s lawn when he was 8 years old. He complained about being paid only $1 per week to mow the lawn. His parents told him that his wage would be doubled every year for mowing the lawn. a) Create a table detailing Malik’s wage as he grew older. b) Graph the data in your table. c) What is the initial value? d) What is the constant ratio? e) Write an equation that represents this pattern. f) If his parents stick to their word, what will be Malik’s wage when he is 16?

Sarah is a customer service representative at a car showroom. She gets paid weekly according to the number of cars she sells. The table details Sarah’s wages depending on the number of cars she sells:

Number of cars	0	1	2	3	4	5
Wage ($)	1428.57	1500	1575	1653.75	3000	1736.44

a) What is Sarah’s base wage? b) Does the table illustrate an exponential pattern? Explain your reasoning. c) What is the constant ratio? d) Write an equation that represents this pattern. e) If Sarah has an incredible week, due to a special offer of 0% financing from the car company, where she sells 9 cars, what will be her wage that week? f) How much more money than her base weekly wage does Sarah make when she sells 9 cars?

Brandon is at war with the mosquitos that cause havoc on his land. Being cognizant of the great benefit of having bees around his property, he has developed an all natural mosquito killer that does not harm the bees. He figures he can reduce the mosquito population each time he sprays by a factor of 0.95. a) Assuming there were 1,000,000 mosquitos before his first spray, determine the number of mosquitoes there were after his 3rd spray. b) Write an equation that calculates the number of mosquitoes after a certain number of sprays. c) Use the equation to determine the number of mosquitoes after his 10th spray. d) If his spray was available commercially, would you buy it to deal with a mosquito problem? Explain your reasoning.

Show/Hide Answer

a)

Age (years) 8 9 10 11 12 13

Wage ($) 1 2 4 8 16 32

b) 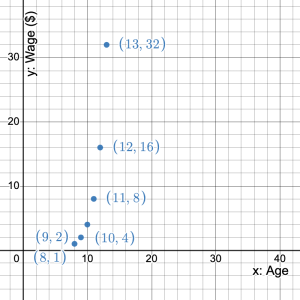c) $1 d) 2 e) Let $n$ = years since age 8 and $y$ = wage, then $y=2^n$ or let $n$ = age and $y$ = wage, then $y=2^{n-8}$ f) $256

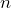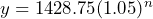a) $1428.57 b) 1500/1428.57 = 1.05; 1575/1500 = 1.05; 1653.75/1575 = 1.05; 3000/1653.75 = 1.05; 1736.44/3000 = 1.05 Since there is a constant ratio, the pattern is exponential. c) 1.05 d) Let $n$ = number of cars sold and $y$ = Sarah’s wage, then $y=1428.75(1.05)^n$ e) $2216.18 f) $787.43
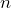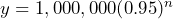a) 1,000,000(0.95)(0.95)(0.95) = 857,375 b) Let $n$ = the number of sprays, and $y$ = the number of mosquitoes, then $y=1,000,000(0.95)^n$ c) 598,737 d) No. Less than half the mosquitoes are dead after 10 sprays! It doesn’t work fast enough.

Skills Icon In this section, we will use what we have learned so far to practice skill problems.

Skill Exercises

Evaluate. If necessary, round to 4 decimal places.

12(3)⁴
50(4)²
1.45(2)⁵
3.4(7)⁰
34(9)¹
21(1.5)²
2.2(0.03)^4
800(1.2)⁵

Show/Hide Answer

972
800
46.4
3.4
306
47.25
0.000001782
1990.656

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

Age (years)	8	9	10	11	12	13
Wage ($)	1	2	4	8	16	32