CHAPTER 7: EXPONENTIAL AND LOGARITHMIC GROWTH
7-1: Exponential Expressions
Exponents
We use multiplication to represent repeated addition. For example, ![]() is shortcut notation for
is shortcut notation for ![]() . Likewise, we use exponents to represent repeated multiplication. For example,
. Likewise, we use exponents to represent repeated multiplication. For example, ![]() can be written
can be written ![]() . The base 5 is multiplied by itself 7 times. 7 is called the exponent. Writing multiple additions or multiple multiplications is tedious and is susceptible to human error, so using multiplication to abbreviate multiple additions, and exponents to abbreviate multiple multiplications makes sense.
. The base 5 is multiplied by itself 7 times. 7 is called the exponent. Writing multiple additions or multiple multiplications is tedious and is susceptible to human error, so using multiplication to abbreviate multiple additions, and exponents to abbreviate multiple multiplications makes sense.
Exponents are used regularly to represent area in square units like ft2 (e.g., a hotel room is 200 square feet) or m2 (e.g., a bedroom is 22 square meters) and volume in cubic units like cm3 (e.g., a box has a volume of 3600 cubic centimeters) or yd3 (e.g., 2 cubic yards of topsoil). So, measuring in two or more dimensions requires the use of exponents on the measurement units.
Any number raised to a power is known as an exponential expression. In section 1-3, we considered powers of 10. We discovered some basic rules that we will see can apply to all numbers.
 Exponential Expressions
Exponential Expressions
Explore 1 – Exponential expressions
Suppose a single bacterium is placed in a petri dish. The number of bacteria in the petri dish doubles every hour. The table shows this growth of bacteria.
| Time (hours) | 0 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|---|
| Bacteria | 1 | 1×2=2
(2=21) |
(1×2) x2=4
(4=22) |
(1x2x2) x2=8
(8=23) |
(1x2x2x2) x2=16
(16=24) |
(1x2x2x2x2) x2=32
(32=25) |
- How do we determine the number of bacteria from one hour to the next?
Solution
We multiply the number of bacteria in the first hour by 2.
- How many bacteria are there after 6 hours?
Solution
After six hours, the number of bacteria is ![]() (i.e.,
(i.e., ![]() ) times the initial number of bacterium, 1.
) times the initial number of bacterium, 1.
- How many bacteria are there after 1 day?
Solution
Since 1 day = 24 hours, there are ![]() bacteria.
bacteria.
- Is it possible to write the number of bacteria at any time as
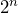 , where n is the number of hours?
, where n is the number of hours?
Solution
Yes. The pattern for the number of bacteria is ![]() for days 0, 1, 2, 3, 4, … The only day that doesn’t appear to be a power of 2 is day 1 when there is 1 bacterium. But,
for days 0, 1, 2, 3, 4, … The only day that doesn’t appear to be a power of 2 is day 1 when there is 1 bacterium. But, ![]() , so the number of bacteria at any time is
, so the number of bacteria at any time is ![]() , where n is the number of hours.
, where n is the number of hours.
To evaluate an exponential expression using a calculator we use either the carat key ![]() or the exponent key
or the exponent key ![]() .To evaluate 224, the input will be
.To evaluate 224, the input will be ![]()
Alternatively, the input is ![]()
Either way, the result is 16,777,216.
 Negative Exponents
Negative Exponents
Explore 2 – Negative exponents
- Knowing that 8 = 23, 4 = 22, 2 = 21, and 1 = 20, follow the pattern to determine what 2-1 and 2-2 equal.
Solution
The pattern 8, 4, 2, 1, … divides each number by 2. Consequently it continues to ![]() . At the same time the pattern 23, 22, 21, 20, continues by reducing the exponent each time by 1 to 2-1, 2-2, 2-3, … This means that
. At the same time the pattern 23, 22, 21, 20, continues by reducing the exponent each time by 1 to 2-1, 2-2, 2-3, … This means that ![]() and
and ![]() .
.
- Use the pattern to write
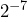 as an expression with a positive exponent.
as an expression with a positive exponent.
Solution
![]()
3. Use the pattern to write ![]() as an expression with a positive exponent.
as an expression with a positive exponent.
Solution
From the pattern, ![]() . So,
. So, ![]()
- Expand your expression to write
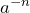 for any non-zero value
for any non-zero value 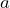 , as an expression with a positive exponent.
, as an expression with a positive exponent.
Solution
![]()
 The Product and Quotient Rules
The Product and Quotient Rules
Explore 3 – The product rule
- Is it true that 2 × 2 × 2 × 2 × 2 is the same as (2 × 2) × (2 × 2 × 2)? Explain your reasoning.
Solution
Yes, they are the same.
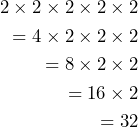 and
and 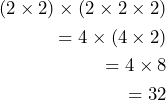
There are two sets of parentheses that change the grouping of the multiplication but do not change the value of the multiplication of the five 2s. This is an example of the associative property of multiplication.
- Considering your answer to #1, is it true that
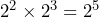 . Explain your reasoning.
. Explain your reasoning.
Solution
Yes. #1 shows us that ![]() . Since
. Since ![]() ,
, ![]() , and
, and ![]() , then
, then ![]() .
.
- Since
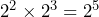 , is there an easy rule to multiply exponential expressions with the same base?
, is there an easy rule to multiply exponential expressions with the same base?
Solution
Yes. Since 2 + 3 = 5, we can keep the common base and add the exponents. This is called the product rule of exponents: ![]()
- Use the product rule to simplify
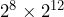
Solution
Since 28 and 212 have the same base 2, we keep the common base and add the exponents: ![]()
- Use the product rule to simplify
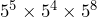
Solution
Since 55, 54, and 58 all have the same base, 5, we keep the common base and add the exponents: ![]()
Explore 4 – The quotient rule
- Simplify
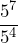 by simplifying the fraction.
by simplifying the fraction.
Solution
![]() .
.
- Use multiplication and the fact that
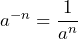 to show that
to show that 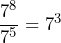
Solution
![]()
- Since
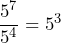 and
and 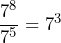 , is there an easy rule to simplify the division?
, is there an easy rule to simplify the division?
Solution
For exponential expressions with the same base, we can divide the expressions by keeping the common base and subtracting the exponents.
- Use your rule to simplify:
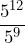
Solution
With a common base of 5, we subtract the exponents: ![]()

- Explain the product rule
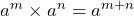 and the quotient rule
and the quotient rule 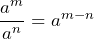 . In particular, explain why it is
. In particular, explain why it is 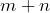 and
and  respectively in the rules.
respectively in the rules.
Show/Hide Answer
It is ![]() in the product rule because
in the product rule because ![]() is multiplied
is multiplied ![]() times and then multiplied
times and then multiplied ![]() times. Therefore,
times. Therefore, ![]() is multiplied
is multiplied ![]() times. It is
times. It is ![]() in the quotient rule because
in the quotient rule because ![]() is multiplied
is multiplied ![]() times, and then divided
times, and then divided ![]() times, which means that
times, which means that ![]() is multiplied
is multiplied ![]() times.
times.
 The Product/Quotient to a Power Rule
The Product/Quotient to a Power Rule
Explore 5 – The product to a power rule
- Evaluate the expression
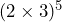 following the order of operations.
following the order of operations.
Solution
The order of operation tells us to first complete the multiplication inside the parentheses: ![]()
Then we evaluate the exponent: ![]()
- Evaluate the expression
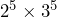 following the order of operations.
following the order of operations.
Solution
First we evaluate the exponents: ![]()
Then we multiply: ![]()
- What do the solutions to 1. and 2. tell us?
Solution
Since the answers are the same (i.e., 7776), ![]() .
.
- Write a rule in English that describes how to simplify
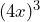 , then use it to complete the simplification.
, then use it to complete the simplification.
Solution
A product to a power, like ![]() , can be simplified by applying the exponent to both factors, then multiplying:
, can be simplified by applying the exponent to both factors, then multiplying: ![]()
- Complete the algebraic rule:
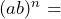
Solution
![]()
Explore 6 – The quotient to a power rule
- Write the expression
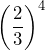 as a product of fractions, then simplify.
as a product of fractions, then simplify.
Solution
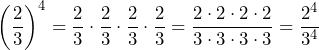
- Write the expression
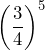 as a product of fractions, then simplify.
as a product of fractions, then simplify.
Solution
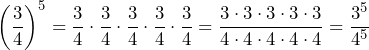
- Write the expression
 as a product of fractions, then simplify.
as a product of fractions, then simplify.
Solution
![]()
- Complete the algebraic rule:
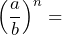
Solution
![]()
- Does your rule work for all values of
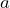 and
and 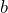 ?
?
Solution
No. Since we cannot divide by zero, ![]()

- Explain the product to a power rule
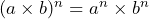 and the quotient to a power rule
and the quotient to a power rule 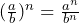 . In particular, explain why the exponent n is applied to to a and b.
. In particular, explain why the exponent n is applied to to a and b.
Show/Hide Answer
For the product to a power rule, the reason ![]() may be applied to
may be applied to ![]() and
and ![]() is that the product
is that the product ![]() is multiplied together
is multiplied together ![]() times. The associative (i.e.,
times. The associative (i.e., ![]() ) and commutative (i.e.,
) and commutative (i.e., ![]() ) properties of multiplication can be applied to get a result that is equal to
) properties of multiplication can be applied to get a result that is equal to ![]() . In other words, we rearrange the
. In other words, we rearrange the ![]() s so that all the
s so that all the ![]() s are together and all the
s are together and all the ![]() s are together.
s are together.
For the quotient to a power rule, the reason ![]() may be applied to
may be applied to ![]() and
and ![]() is that the fraction
is that the fraction ![]() is multiplied together
is multiplied together ![]() times. We multiply all the numerators and put the result in the numerator and multiply all the denominators and put the result in the denominator. There are
times. We multiply all the numerators and put the result in the numerator and multiply all the denominators and put the result in the denominator. There are ![]() terms of
terms of ![]() ‘s multiplied together in the numerator and
‘s multiplied together in the numerator and ![]() terms of
terms of ![]() in the denominator multiplied together. Therefore, the result is
in the denominator multiplied together. Therefore, the result is ![]() .
.
 Power to a Power Rule
Power to a Power Rule
Explore 7 – Power to a power rule
To understand the exponential expression ![]() , Nina starts with the exponent 4, and comes up with the equivalent expression
, Nina starts with the exponent 4, and comes up with the equivalent expression ![]() .
.
- Explain why there are four
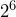 terms.
terms.
Solution
The meaning of the exponent 4 means there are four of the base ![]() that are multiplied together. Therefore,
that are multiplied together. Therefore, ![]() .
.
- How many 2’s are there in total in the multiplication?
Solution
Based on the product rule of exponents, ![]() . Therefore, there are 24 twos multiplied together.
. Therefore, there are 24 twos multiplied together.
- Nina explains that the total number of 2’s is 6 x 4 = 24. Why can Nina multiply the two powers?
Solution
It is because there are four ![]() multiplied together. The total number of 2 that are multiplied together is
multiplied together. The total number of 2 that are multiplied together is ![]() .
.
- Write a rule that simplifies a power raised to a power, then use it to simplify
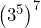 .
.
Solution
![]()
![]()
Explore 8 – Power to a power rule
A population of bacteria doubles six times in one hour.
- Jonas says the population after 4 hours will be
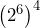 times the initial population. Is he correct? Explain your reasoning.
times the initial population. Is he correct? Explain your reasoning.
Solution
Doubling six times in one hour means the population doubles every 10 minutes. If the initial population is ![]() then after the first 10 minutes there will be
then after the first 10 minutes there will be ![]() ; then after the second 10 minutes there are
; then after the second 10 minutes there are ![]() ; then after the third 10 minutes there are
; then after the third 10 minutes there are ![]() ; …so after the sixth 10 minutes (i.e., one hour) there will be
; …so after the sixth 10 minutes (i.e., one hour) there will be ![]() bacteria.
bacteria.
Consequently, after 4 hours there will be ![]() .
.
- Simplify
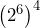 without using any exponents.
without using any exponents.
Solution
![]()
- Simplify
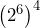 using the product rule of exponents.
using the product rule of exponents.
Solution
![]() .
.
- Simplify
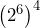 using the power to a power rule.
using the power to a power rule.
Solution
![]() .
.

- Explain the power to a power rule
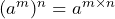 . In particular, explain why it is
. In particular, explain why it is 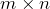 .
.
Show/Hide Answer
Since there are ![]() of
of ![]() multiplied together, it shows
multiplied together, it shows ![]() . Since there are
. Since there are ![]() of
of ![]() , the sum of the addition of
, the sum of the addition of ![]() ‘s is
‘s is ![]() . Therefore,
. Therefore, ![]() .
.
Rules of Exponents
| Rule | Description | Symbolic Definition |
|---|---|---|
| Exponent of 1: | Any number to the power 1 equals the number. | |
| Zero Exponent: | Any non-zero number to the power zero equals 1. | |
| Product Rule |
Two or more exponential expressions with the same base can be multiplied by keeping the common base and adding the exponents. |
|
| Quotient Rule |
Two exponential expressions with the same base can be divided by keeping the common base and subtracting the exponents. |
|
| Negative Exponents |
When an exponential expression has a negative exponent the number is a fraction of a whole. |
|
| Product to a Power Rule |
A product can be raised to a power by multiplying each factor raised to the power. |
|
| Quotient to a Power Rule |
A quotient raised to a power can be split into the numerator raised to the power divided by the denominator raised to the power. |
|
| Power to a Power Rule |
To raise a power to a power, keep the base and multiply the exponents. |
Example
- The number of people waiting for a train that is running late doubles every 15 minutes. a) Complete the table to show how the number of people has grown over time. b) Write an expression that shows the growth after an hour. c) The next train is almost due, but the late train has not yet arrived. Consequently, the number of people waiting for the train triples every 15 minutes after the first hour. Complete the table for the second hour. c) Simplify the exponential form after 2 hours. d) If there were originally three people waiting for the train, how many people are waiting on the train after 2 hours? e) If each train carriage holds 630 passengers, how many carriages will be needed to accommodate the waiting passengers after 2 hours?
| Time (hours) | 0 | 0.25 | 0.5 | 0.75 | 1 | 1.25 | 1.5 | 1.75 | 2 |
|---|---|---|---|---|---|---|---|---|---|
| People | |||||||||
| Exponential form |
Show/Hide Answer
-
Time (hours) 0 0.25 0.5 0.75 1 1.25 1.5 1.75 2 People 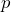
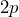
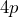
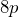
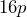
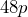
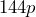
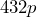
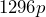
Exponential form 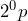
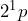
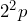
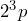
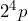
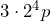
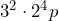
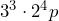
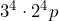
c)
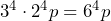 d)
d) 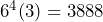 e) 3888/630 = 6.2; 7 carriages will be required.
e) 3888/630 = 6.2; 7 carriages will be required.
Practice Exercises
Use the rules of exponents to simplify. Leave your answers with only positive exponents.
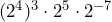
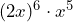
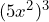
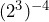
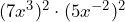
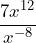
- Nathan says
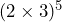 is the same as
is the same as 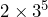 . Is he correct? Explain your reasoning.
. Is he correct? Explain your reasoning.
Show/Hide Answer
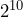
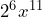
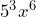
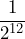
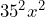
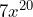
- No.
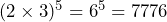 , while
, while 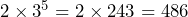 .
.
 In this section, we will take what we have learned and apply the concepts to new situations.
In this section, we will take what we have learned and apply the concepts to new situations.
Perspectives
- Jean is moving apartments and doesn’t want to take all of her junk with her when she moves. She has decided to throw away 1 item the first day, then double that number of items she discards each day over the next week. a) Create a table to show how many items will be discarded each day. b) How many items will she discard on day
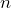 ?
? - A population of rabbits doubles every 10 days. a) Create a table to show how many rabbits there are in the population over time if there were initially
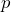 rabbits in the population. b) Write an algebraic expression showing how many rabbits there are after
rabbits in the population. b) Write an algebraic expression showing how many rabbits there are after 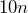 days. c) If left unchecked, how many rabbits will there be after 360 days?
days. c) If left unchecked, how many rabbits will there be after 360 days? - Adriel deposits $5000 into his bank account. The account balance increases to 1.015 times the balance every year. What is the account balance after 10 years? Show your work using exponents.
- The population of a species doubles every month from January to April, and then reduces by half every month for the following two months. a) Write the population increase-decrease pattern in a mathematical sentence without using exponents. b) Write the population increase-decrease pattern in a mathematical sentence using exponents. c) Simplify the expression using the rules of exponents.
- A video clip goes viral. The number of people who view the clip doubles every 15 minutes for the first six hours, and then triples every 12 hours for the next 4 days. Write the population growth as a mathematical sentence using exponents.
Show/Hide Answer
- a)
Day 1 2 3 4 5 6 7 Number of items 1 2 4 8 16 32 64
b) ![]()
- a)
Number of days 0 10 20 30 40 50 Number of rabbits 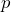
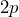
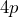
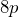
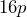
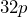
b) ![]() c)
c) ![]()
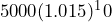 = $5802.70
= $5802.70- a)
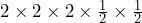 b)
b) 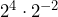 c)
c) 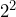
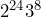
 In this section, we will use what we have learned so far to practice skill problems.
In this section, we will use what we have learned so far to practice skill problems.
Skill Exercises
Evaluate:
- 34
- 0.25
- 40
- 1.24
- 2-3
- 1.5-2
Simplify:
- 34 · 35
- 148 · 14
- 1.57 · 1.53
- 67 ÷ 64
- 1.0312 ÷ 1.039
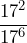
- 5-2 ÷ 57
- (2 · 3)4
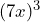
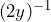
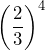
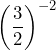
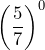
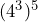
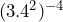
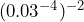
Show/Hide Answer
- 81
- 0.00032
- 1
- 3.8416
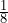
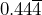
- 39
- 149
- 1.510
- 63
- 1.033
- 17-4 =
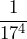
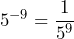
- 64
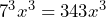
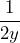
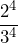
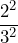
- 1
- 415
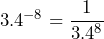
- 0.038
the number of times a base number is multiplied by itself
the amount of space inside a two-dimensional object measured in square units
a measure of the amount of 3-dimensional space an object takes up


