CHAPTER 6: LINEAR GROWTH
6-4: Linear Modeling – Linear Equations in Two Variables
Introduction
Using linear reasoning we have seen that linear patterns can be seen as a constant rate and initial value, paired data in a table, or coordinates on a graph that lie on a line. We can also use linear reasoning in any of the three formats to transform the data into an equation. Such an equation shows the relationship between the independent and dependent values, and since that relationship is linear, we call the equation a linear equation.
 Constructing an Equation using Linear Reasoning
Constructing an Equation using Linear Reasoning
We have already seen that linear reasoning starts with an initial value, and adds a constant rate of change multiple times. To simplify the multiple additions, we used multiplication of the constant rate of change by a given independent value to obtain the dependent value we are trying to find. For example, suppose the drop fee of a taxi ride is $10, and you are charged an additional mileage fee of $1.50 per mile traveled. If you travel 5 miles, the cost would be $10 + ($1.50/mile)(5 miles). So, if you travel ![]() miles the cost would be
miles the cost would be ![]() . So, we can generate an equation that will allow us to determine the cost of the taxi ride for any number of miles. That is, we take a specific example of traveling 5 miles to a general equation of traveling any number of miles.
. So, we can generate an equation that will allow us to determine the cost of the taxi ride for any number of miles. That is, we take a specific example of traveling 5 miles to a general equation of traveling any number of miles.
Explore 1 – Identify independent and dependent values and their units
Determine the independent and dependent values for each rate below. Explain how the independent value determines the dependent value. Give an example of a possible real-life scenario for each rate.
- $6.25 per kg.
Solution
The independent value is 1 kg. The dependent value is $6.25. The money increases by $6.25 as the weight increases by 1 kg. A possible scenario for the rate is the money you get by selling aluminum cans in kilograms to a recycler.
- 65 miles per hour
Solution
The independent value is 1 hour. The dependent value is 65 miles. The distance increases 65 miles as the time increases by 1 hour. A possible scenario for the rate is the speed of a car traveling at 65 mph.
Solution
The independent value is 3 items. The dependent value is $8. The money increases by $8 as the number of items increases by 3. A possible scenario for the rate is the price of goods in a supermarket.
Solution
The independent value is 2 hours. The dependent value is –3 inches. It decreases by 3 inches as the time increases by 2 hours. A possible scenario for the rate is the decrease of water level in a child’s wading pool.
Explore 2 – Identify the independent variable and dependent variable
- If a movie ticket costs $8.50, the total cost,
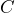 , of buying
, of buying 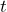 tickets is
tickets is 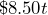 . Is
. Is 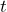 the independent variable or the dependent variable? Is
the independent variable or the dependent variable? Is 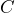 the independent variable or the dependent variable? Explain your reasoning.
the independent variable or the dependent variable? Explain your reasoning.
Solution
![]() is the independent variable and
is the independent variable and ![]() is the dependent variable. Knowing that the rate is $8.50 per ticket, the independent value is one ticket. Therefore, the independent variable is the number of tickets,
is the dependent variable. Knowing that the rate is $8.50 per ticket, the independent value is one ticket. Therefore, the independent variable is the number of tickets, ![]() . Since the dependent value is $8.50, the dependent variable is the cost that has the unit dollars. Therefore,
. Since the dependent value is $8.50, the dependent variable is the cost that has the unit dollars. Therefore, ![]() is the dependent variable. In other words, the total cost,
is the dependent variable. In other words, the total cost, ![]() , depends upon the number of tickets purchased,
, depends upon the number of tickets purchased, ![]() .
.
- Kelsey is a part-time student worker at UVU. She gets paid $15.50 per hour and works up to 28 hours per week. She gets paid every two weeks. Her gross pay,
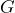 , can be found by multiplying the number of hours she works,
, can be found by multiplying the number of hours she works, 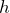 , by
, by 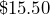 . What is the independent variable and what is the dependent variable? Explain your reasoning.
. What is the independent variable and what is the dependent variable? Explain your reasoning.
Solution
![]() is the independent variable and
is the independent variable and ![]() is the dependent variable. Knowing that the rate is $15.50 per hour, the independent value is one hour and the dependent value is $15.50. Therefore, the independent variable is the number of hours,
is the dependent variable. Knowing that the rate is $15.50 per hour, the independent value is one hour and the dependent value is $15.50. Therefore, the independent variable is the number of hours, ![]() , and the dependent variable is the gross pay,
, and the dependent variable is the gross pay, ![]() . In other words, the gross pay,
. In other words, the gross pay, ![]() , depends upon the number of hours worked,
, depends upon the number of hours worked, ![]() .
.
Explore 3 – Write the equation for a positive linear rate
A gym charges a signup fee of $50. It then charges $40 per month to use the facilities.
- Does this represent a linear pattern? Explain your reasoning.
Solution
Yes. It has an initial value of $50 and a constant rate of change of $40 per month.
- How much would it cost to sign up and use the gym for 1 month?
Solution
The total cost = signup fee + monthly charge = $50 + $40/month · 1 month = $50 + $40 = $90
- How much would it cost to sign up and use the gym for 6 months?
Solution
The total cost = signup fee + monthly charges = $50 + $40/month · 6 months = $50 + $240 = $290
- How much would it cost to sign up and use the gym for 9 months?
Solution
The total cost = signup fee + monthly charges = $50 + $40/month · 9 months = $50 + $360 = $410
- Explain in words how to determine the total cost of signing up and using the gym.
Solution
The total cost equals the signup fee plus the monthly rate times the number of months.
- If
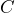 = the total cost, and
= the total cost, and 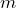 = the number of months, write an equation that shows the total cost to sign up and use the gym for
= the number of months, write an equation that shows the total cost to sign up and use the gym for 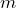 months.
months.
Solution
![]()
- Use your equation to determine the total cost of signing up and using the gym for 2 years.
Solution
Since 2 years = 24 months, ![]() . So,
. So, ![]() . The total cost os $1010.
. The total cost os $1010.
Linear Patterns as Equations
Explore 4 – Write the equation for a positive linear rate
Use linear reasoning to write the equation for each of the following linear patterns. Use the variable ![]() for the independent variable and
for the independent variable and ![]() for the dependent variable. After writing the equation, substitute a value for
for the dependent variable. After writing the equation, substitute a value for ![]() that makes sense to the situation to determine the value of
that makes sense to the situation to determine the value of ![]() . Then explain what the values of
. Then explain what the values of ![]() and
and ![]() mean.
mean.
- John purchases some bananas that cost $0.49 per pound.
Solution
The initial value is $0 since it costs nothing to buy nothing. Therefore, the equation is ![]()
If ![]() , then
, then ![]() . This means if John purchases 10 pounds of bananas, the cost will be $4.90.
. This means if John purchases 10 pounds of bananas, the cost will be $4.90.
- A car travels at 65 miles per hour towards Las Vegas, with 100 miles already completed.
Solution
The initial value = 100 miles and the rate of change = 65 mph. Therefore, the equation is ![]()
If ![]() ,
, ![]() . This means the car traveled a total of 295 miles in three hours toward Las Vegas.
. This means the car traveled a total of 295 miles in three hours toward Las Vegas.
- Kaye rents a truck that charges a $29.99 base fee and a mileage fee of $0.75 per mile.
Solution
The initial value is $29.99 and the rate of change is $0.75 per mile. Therefore, the equation is ![]()
If ![]() ,
, ![]() . This means Kaye’s total rental charge will be $44.99 if she travels 20 miles.
. This means Kaye’s total rental charge will be $44.99 if she travels 20 miles.
- A nurse gives a patient the first dose of 10mg of medicine followed by the rate
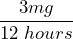 .
.
Solution
The initial value is 10mg and the rate of change is ![]() , which simplifies to 0.25mg per hour.
, which simplifies to 0.25mg per hour.
Therefore, the equation is ![]()
If ![]() ,
, ![]() . This means the total amount of medicine the patient receives is 19 milligrams over 36 hours.
. This means the total amount of medicine the patient receives is 19 milligrams over 36 hours.
Explore 5 – Write the equation for a negative linear rate
Use linear reasoning to write the equation for each of the following linear patterns. Use the variable ![]() for the independent variable and
for the independent variable and ![]() for the dependent variable. After writing the equation, substitute a value for
for the dependent variable. After writing the equation, substitute a value for ![]() that makes sense to the situation to determine the value of
that makes sense to the situation to determine the value of ![]() . Then explain what the values of
. Then explain what the values of ![]() and
and ![]() mean.
mean.
- The water level of a lake is dropping 2 inches per day due to evaporation and a recent drought. The current water level is 120 inches.
Solution
The initial value is 120 inches. The rate of change is –2 inches per day. The rate is negative because the water level is dropping.
Therefore the equation is ![]()
If ![]() , then
, then ![]() . This means the depth of the lake will be 60 inches after 30 days if the drought continues.
. This means the depth of the lake will be 60 inches after 30 days if the drought continues.
- A car depreciates at an average rate of $2000 per year. The current value of a car is $32,000.
Solution
The initial value is $32,000 and the rate of change = –$2000 per year. Therefore, the equation is ![]() .
.
If ![]() , then
, then ![]() . This means the value of the car will drop to $12,000 after 10 years.
. This means the value of the car will drop to $12,000 after 10 years.
When we use a linear pattern to identify the initial value and the rate of change, then write an equation of the form Dependent variable = Initial value + Rate of change · Independent variable, we are writing a linear equation.
Writing a Linear Equation
If ![]() = Dependent variable,
= Dependent variable, ![]() = Initial value, and
= Initial value, and ![]() = Rate of change, the linear equation is:
= Rate of change, the linear equation is:
![]() or
or ![]()
Notice that ![]() and
and ![]() are equivalent. However, in math it is common practice to write the variable term before the constant term, so
are equivalent. However, in math it is common practice to write the variable term before the constant term, so ![]() is more likely to be seen in math textbooks or in online help videos.
is more likely to be seen in math textbooks or in online help videos.
Example
A MacBook Pro battery has a 100Wh capacity. A fully charged laptop battery loses 5% of its maximum capacity every hour when Ian searches the Internet. Suppose ![]() represents the percent of battery power remaining after
represents the percent of battery power remaining after ![]() hours of searching the Internet.
hours of searching the Internet.
- What is the initial value of
 ? Explain what this value means.
? Explain what this value means. - What is the constant rate of change?
- Write an equation that represents
 in terms of
in terms of  .
. - Use the equation to determine the battery power after 3 hours.
- Use the equation to determine the battery power after 10 hours.
- Use the equation to determine when the battery power is at zero
Show/Hide Answer
- 100%. The battery is fully charged.
- –5% per hour
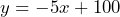
- 85%
- 50%
- 20 hours

- The equation for a linear pattern is
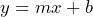 where
where 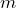 is the rate of change and
is the rate of change and 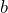 is the initial value. Additionally,
is the initial value. Additionally,  is the independent variable and
is the independent variable and  is the dependent variable. Explain the meaning of
is the dependent variable. Explain the meaning of 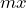 ,
, 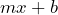 , and
, and 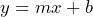 .
.
Show/Hide Answer
The term ![]() represents the rate
represents the rate ![]() times the independent variable
times the independent variable ![]() . It tells us the change in the dependent variable
. It tells us the change in the dependent variable ![]() given a change in the independent variable
given a change in the independent variable ![]() . It is the amount that is added to the initial value.
. It is the amount that is added to the initial value.
The combination of the two terms ![]() adds the change in the value of
adds the change in the value of ![]() given a change in
given a change in ![]() to the initial value. It tells us the total value of the dependent variable given any value of the independent variable.
to the initial value. It tells us the total value of the dependent variable given any value of the independent variable.
The equation ![]() shows the relationship between the independent variable
shows the relationship between the independent variable ![]() and the dependent variable
and the dependent variable ![]() . It allows us to calculate the value of
. It allows us to calculate the value of ![]() given any value of
given any value of ![]() .
.
 Construct a Linear Equation from a Table
Construct a Linear Equation from a Table
Explore 6 – Write a linear equation from a table showing a constant rate of change
The table shows the salary of a person.
| Hours Worked | Salary ($) |
|---|---|
| 0 | 200 |
| 1 | 210 |
| 2 | 220 |
| 3 | 230 |
| 4 | 240 |
- What is the rate of change? Does this show a linear pattern?
Solution
The rate is $10 per hour because the salary increases $10 as the number of hours increases by 1. Yes this is a linear pattern since the rate of change is constant at $10/hour.
- Identify the independent and dependent variables along with their units, and the initial value.
Solution
The independent variable is hours worked measured in hours and the dependent variable is salary measured in dollars. The initial value is $200.
- Write an equation for the linear pattern in the table.
Solution
Let ![]() = hours worked and
= hours worked and ![]() = salary. Then,
= salary. Then, ![]()
- What could the initial value represents in this scenario?
Solution
The initial value of $200 could be a transportation stipend, a meal stipend, or a base wage.
Explore 7 – Write a linear equation from a table with a negative rate of change
The table shows the air temperature over time.
| Time passed (Hours) | Temperature (° Fahrenheit) |
|---|---|
| 0 | 56 |
| 1 | 52 |
| 2 | 48 |
| 3 | 44 |
| 4 | 40 |
- What is the rate of change? Does this show a linear pattern?
Solution
The rate is –4 degrees Fahrenheit per hour because the temperature drops 6 degrees Fahrenheit every hour. Yes this is a linear pattern since the rate of change is constant at –4°F/hour.
- Identify the independent and dependent variables along with their units, and the initial value.
Solution
The independent variable is time passed measured in hours and the dependent variable is temperature measured in degrees Fahrenheit. The initial temperature is 56°F.
- Write an equation for the linear pattern in the table.
Solution
Let ![]() = time passed and
= time passed and ![]() = temperature. Then,
= temperature. Then, ![]()
- What do you think the initial value represents in this temperature scenario?
Solution
The initial value of 56 degrees Fahrenheit is the starting temperature, so could be the high temperature of the day before the sun goes down and the temperatures start to fall.
Examples
- The table shows the cost to play video games at a Game Shop.
| Number of Games | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| Cost ($) | 2.50 | 2.60 | 2.70 | 2.80 | 2.90 |
- a) What is the initial value and what does it represent?
- b) What is the rate of change and what does it tell us?
- c) If
 = the number of games and
= the number of games and  = the cost, write an equation that represents this data.
= the cost, write an equation that represents this data. - d) What are the restrictions on the values of
 ?
? - e) Use your equation to determine the cost to play 10 games.
- f) Use your equation to determine the cost to play 25 games.
- The table shows the weight of a person on a diet over time.
| Time (Weeks) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|---|
| Weight (lb.) | 254 | 251 | 248 | 245 | 242 | 239 | 236 | 233 | 230 |
a) What is the initial value and what does it represent? b) What is the rate of change and what does it tell us? c) How long will it take the person to reach their first goal of weighing 200 lb? d) How long will it take this person to lose 90 lb. and hit their target weight? e) If ![]() = time and
= time and ![]() = weight, write an equation that represents this data. f) Use your equation to determine the person’s weight after 20 weeks.
= weight, write an equation that represents this data. f) Use your equation to determine the person’s weight after 20 weeks.
Show/Hide Answer
- a) $2.50. The cost to enter the Game Shop. b) $0.10 per game = 10¢ per game. The increase in cost to play 1 more game. c)
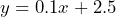 d)
d)  must be a whole number e) $3.50 f) $5
must be a whole number e) $3.50 f) $5 - a) 254 lb. The person’s starting weight. b) –3 lb. per week. The person is losing 3 pounds per week. c) 18 weeks d) 30 weeks e)
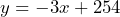 f) 194 lb.
f) 194 lb.

- A linear equation takes the form
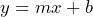 where
where 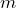 is the rate of change and
is the rate of change and 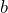 is the initial value. Explain how to identify
is the initial value. Explain how to identify 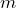 and
and 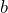 from a table showing a linear pattern.
from a table showing a linear pattern.
Show/Hide Answer
You determine the rate of change ![]() by calculating the change in the value of the dependent variable per the change in the value of the independent variable. The fraction will have the numerator as the change in the dependent variable values and the denominator the change in the independent variable values. If
by calculating the change in the value of the dependent variable per the change in the value of the independent variable. The fraction will have the numerator as the change in the dependent variable values and the denominator the change in the independent variable values. If ![]() ,
, ![]() and
and ![]() ,
, ![]() are two pairs of values in a table,
are two pairs of values in a table, ![]() is the change in the value of the dependent variable and
is the change in the value of the dependent variable and ![]() is the change in the value of the independent variable. Therefore, the rate
is the change in the value of the independent variable. Therefore, the rate ![]() . The initial value is the value of the dependent variable when the independent variable equals zero.
. The initial value is the value of the dependent variable when the independent variable equals zero.
| Independent values |
Dependent values |
|---|---|
 Constructing a Linear Equation from a Graph
Constructing a Linear Equation from a Graph
Explore 8 – Write the equation of a linear graph with a positive slope
The graph shows the total charge for an online purchase of a number of items with a set shipping fee.
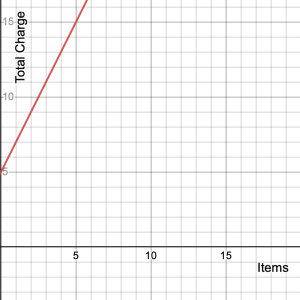
- Identify the independent and dependent variables.
Solution
The independent variable is the number of items (shown on the ![]() -axis). The dependent variable is the total charge (shown on the
-axis). The dependent variable is the total charge (shown on the ![]() -axis).
-axis).
- Find the rate of change by using two points on the line.
Solution
The rate of change = the slope of the line.
Using the two points (0, 5) and (1, 7) on the line, the difference in ![]() -coordinates (7 – 5 = 2) shows the increase in total charge of $2 (the rise). The difference in
-coordinates (7 – 5 = 2) shows the increase in total charge of $2 (the rise). The difference in ![]() -coordinates (1 – 0 = 1) shows an increase of 1 in the number of items (the run).
-coordinates (1 – 0 = 1) shows an increase of 1 in the number of items (the run).
Therefore, the slope is ![]() , and the rate of change is $2 per item.
, and the rate of change is $2 per item.
- Find the shipping fee.
Solution
The shipping fee is the initial value. On the graph the initial value is found at the ![]() -intercept. The
-intercept. The ![]() -intercept = (0, 5) so the initial value is $5. Therefore, the shipping fee is $5.
-intercept = (0, 5) so the initial value is $5. Therefore, the shipping fee is $5.
- Write an equation that represents the linear graph.
Solution
The rate of change is 2 and the initial value is 5, so the equation is ![]() .
.
The rate of change of a linear pattern = the slope of the line formed by graphing the data pairs on a coordinate system. If the points ![]() and
and ![]() lie on a line, the slope of the line is found by first determining the rise and the run. The rise =
lie on a line, the slope of the line is found by first determining the rise and the run. The rise = ![]() and the run =
and the run = ![]() . Therefore, the slope =
. Therefore, the slope = ![]() .
.
Slope of a Line
If ![]() and
and ![]() are points that lie on a line, and
are points that lie on a line, and ![]() = the slope of the line,
= the slope of the line,
![]()
Explore 9 – Write the equation of a linear graph with a negative slope
The graph shows a temperature drop in degrees Celsius over time.
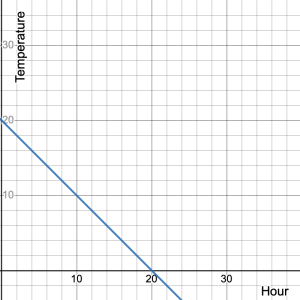
- Identify the independent and dependent variables along with their units.
Solution
The independent variable is time, shown on the ![]() -axis and measured in hours. The dependent variable is temperature, shown on the
-axis and measured in hours. The dependent variable is temperature, shown on the ![]() -axis and measured in degrees Celsius.
-axis and measured in degrees Celsius.
- Find the rate of change and initial value.
Solution
The rate of change = the slope of the line: ![]()
Using the points (0, 20) and (20, 0), ![]() . Therefore, the rate of change = –1°C per hour.
. Therefore, the rate of change = –1°C per hour.
The initial value is found at the ![]() -intercept which is (0, 20). Therefore, the initial value is 20°C.
-intercept which is (0, 20). Therefore, the initial value is 20°C.
- Write an equation that represents the linear graph.
Solution
Since the rate of change = –1 and the initial value = 20, the equation is ![]() .
.

- The linear equation
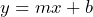 where
where 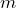 is the rate of change (or slope of the line) and
is the rate of change (or slope of the line) and 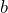 is the initial value (or
is the initial value (or  -intercept
-intercept 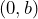 ). Explain how determine
). Explain how determine 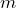 and
and 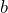 from a linear graph (a line) on the coordinate plane.
from a linear graph (a line) on the coordinate plane.
Show/Hide Answer
The rate or slope ![]() can be obtained by determining the rise over the run where the rise is the change in the values of the dependent variable between two points and the run is the change in the corresponding values of the independent variable. If the points
can be obtained by determining the rise over the run where the rise is the change in the values of the dependent variable between two points and the run is the change in the corresponding values of the independent variable. If the points ![]() and
and ![]() lie on the line, the slope of the line is found by first determining the rise and the run. The rise =
lie on the line, the slope of the line is found by first determining the rise and the run. The rise = ![]() and the run =
and the run = ![]() . Therefore, the slope =
. Therefore, the slope = ![]() .
.
The initial value ![]() is the
is the ![]() -coordinate of the
-coordinate of the ![]() -intercept.
-intercept.
Practice Exercises
- In 1995, 41 grey wolves were relocated to Yellowstone National Park in an effort to regain a native wolf population. Researchers estimate that the wolf population has been growing by approximately 12 wolves every year. a) What are the independent and dependent variables? b) What is the initial value? c) What is the rate of change? d) If
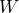 = the number of wolves and
= the number of wolves and 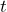 = the number of years since 1995, write an equation that represents the number of wolves over time. e) How many wolves were in the park in 1998? f) How many wolves were in the park in 2000? g) According to the equation, how many wolves were in the park in 2022? h) Will the population continue to grow at 12 wolves every year? What could affect that number?
= the number of years since 1995, write an equation that represents the number of wolves over time. e) How many wolves were in the park in 1998? f) How many wolves were in the park in 2000? g) According to the equation, how many wolves were in the park in 2022? h) Will the population continue to grow at 12 wolves every year? What could affect that number? - Rebekah deposits $20,000 in a high interest savings account that pays 5% annual simple interest. a) What is the rate of change? b) Write an equation that represents the account’s value over time in years. c) How much will be in the account after 1 year? d) How much will be in the account after 5 years? e) How long will it take for Rebekah to have $50,000 in the account?
Show/Hide Answer
- a) Independent = time in years since 1995, dependent = number of wolves in Yellowstone b) 41 wolves c) 12 wolves per year d)
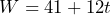 or
or 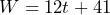 e) 77 f) 101 g) 365 h) No. The more wolves there are the more likely there are to be more pups born. Wolves also die every year, which would reduce the numbers. Wolves will leave the park and may be shot by ranchers. As of January 2023, there are at least 108 wolves in the park spread between 10 packs.[1]
e) 77 f) 101 g) 365 h) No. The more wolves there are the more likely there are to be more pups born. Wolves also die every year, which would reduce the numbers. Wolves will leave the park and may be shot by ranchers. As of January 2023, there are at least 108 wolves in the park spread between 10 packs.[1] - a) $1000 per year b) Let
 = number of years and
= number of years and  = value of the account, then
= value of the account, then 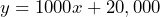 c) $21,000 d) $25,000 e) 30 years
c) $21,000 d) $25,000 e) 30 years
 In this section, we will take what we have learned and apply the concepts to new situations.
In this section, we will take what we have learned and apply the concepts to new situations.
Perspectives
- A gym charges a membership fee of $75 to join, and $35 per month to use the facility. a) Define the variables and write an equation that represents the total cost of joining and using the gym. b) Use the equation to determine the total cost of joining and using the gym for 1 year. c) Use the equation to determine how long Harry can belong to the gym if she pays $705.
- It is snowing outside. There are currently 5 inches of snow on the ground. Suppose the snow is accumulating at 2 inches every hour. a) If
 = the time it has been snowing in hours, and
= the time it has been snowing in hours, and  =the depth of snow on the ground, write an equation that represents the depth of snow over time. b) What is the snow depth after 5 hours? c) If it keeps snowing at the same rate of accumulation, how long will it take till there are 2 feet of snow on the ground?
=the depth of snow on the ground, write an equation that represents the depth of snow over time. b) What is the snow depth after 5 hours? c) If it keeps snowing at the same rate of accumulation, how long will it take till there are 2 feet of snow on the ground? - The water level of Utah Lake is dropping at 0.1 inches every day. It’s current average depth is 9 feet 2 inches. a) If
 = time in days from now, and
= time in days from now, and  = the average depth of the lake in inches, write an equation that represents the average depth of the lake over time. b) Use your equation to determine the average depth of the lake in 30 days. c) Use your equation to determine the average depth of the lake in one year. d) Use your equation to determine when the average depth of the lake will be dry.
= the average depth of the lake in inches, write an equation that represents the average depth of the lake over time. b) Use your equation to determine the average depth of the lake in 30 days. c) Use your equation to determine the average depth of the lake in one year. d) Use your equation to determine when the average depth of the lake will be dry. - Heather needs to order official transcripts to apply to graduate schools. The university charges $5 per transcript and a processing fee of $2.50. a) Write an equation that represents the cost of ordering transcripts. b) How much will it cost to order 4 transcripts? c) How much will it cost to order 9 transcripts?
- The temperature decreases by 3.3°F for every 1000 feet gain in elevation. Suppose you are at the trailhead of Timpanogos Mountain at Sundance. Timpanogos Mountain has an elevation of 11,752 feet, while Sundance has an elevation of 4738 feet. a) Write an equation to represent the temperature,
 , after climbing
, after climbing  thousand feet up Timpanogos Mountain if the temperature at Sundance is 75°F. b) What is the temperature at the top of the mountain?
thousand feet up Timpanogos Mountain if the temperature at Sundance is 75°F. b) What is the temperature at the top of the mountain? - A strong thunderstorm flooded Tobin’s basement. He uses a pump to extract the water. The water depth drops 0.25 inches per minute. The current water depth is 1.5 feet. a) What is the rate of change to the depth of water? b) What is the initial value? c) Write an equation that represents the depth of water,
 , if the pump has been running for
, if the pump has been running for  minutes. d) What will be the depth of water after 30 minutes of pumping? e) How long will it take to pump out all the water?
minutes. d) What will be the depth of water after 30 minutes of pumping? e) How long will it take to pump out all the water? - Jason graduated from college and got a job in 2012. His salary has been raised by a constant amount every year since 2014. Jason’s salary was $58,500 in 2016 and $78,500 in 2020. a) What was Jason’s annual pay raise since 2014? b) Make a table or use linear reasoning to determine Jason’s annual salary in 2015. c) What is the initial value of the linear pattern for salary? d) Why does the linear pattern not start in 2012? e) Write an equation that represents Jason’s salary over time. f) If the pattern continued at the same rate of change, how much did Jason earn in 2020? g) If the pattern continues at the same rate of change, how much is Jason earning now?
Show/Hide Answer
- a) Let
 = number of months and
= number of months and  = total cost, then
= total cost, then 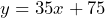 b) $495 c) 18 months
b) $495 c) 18 months - a)
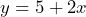 or
or 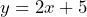 b) 10 inches c) 9.5 hours
b) 10 inches c) 9.5 hours - a)
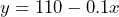 or
or 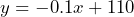 b) 107 inches = 8 feet 11 inches c) 73.5 inches = 6 feet 1.5 inches. d) 1100 days = 3 years 5 days (assuming no leap year)
b) 107 inches = 8 feet 11 inches c) 73.5 inches = 6 feet 1.5 inches. d) 1100 days = 3 years 5 days (assuming no leap year) - a) Let
 = the number of transcripts and
= the number of transcripts and  = the cost, then
= the cost, then 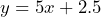 b) $22.50 c) $47.50
b) $22.50 c) $47.50 - a)
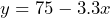 or
or 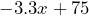 b) 36.2°F
b) 36.2°F - a) –0.25 inches per minute b) 18 inches. c)
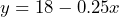 or
or 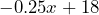 d) 10.5 inches. e) 72 minutes = 1 hour 12 minutes
d) 10.5 inches. e) 72 minutes = 1 hour 12 minutes - a) $10,000 per year. b) $68,500 c) $38,500 d) The raises started in 2014. e) Let
 = time since 2014 and
= time since 2014 and  = salary in thousands of dollars, then
= salary in thousands of dollars, then 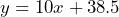 f) $98,500 g) Answers vary:
f) $98,500 g) Answers vary:  =current year – 2014. Substitute
=current year – 2014. Substitute  -value into equation and solve for
-value into equation and solve for  .
.
 In this section, we will use what we have learned so far to practice skill problems.
In this section, we will use what we have learned so far to practice skill problems.
Skill Exercises
Write an equation in ![]() and
and ![]() that represents the information:
that represents the information:
- Slope = 3;
 -intercept = (0, 5)
-intercept = (0, 5) - Slope = –4;
 -intercept = (0, –1)
-intercept = (0, –1) - Slope = 3/4;
 -intercept = (0, 1)
-intercept = (0, 1) - Slope = –5/2;
 -intercept = (0, 3)
-intercept = (0, 3) - Slope = 0.2;
 -intercept = (0, –7)
-intercept = (0, –7)
Determine the slope of the line that passes through the two points:
- (0, 3) and (1, 7)
- (0, –5) and (1, 5)
- (0, –2) and (2, 0)
- (2, 3) and (4, 6)
- (–1, 4) and (3, 8)
- (–2, –3) and (4, 5)
- (2, 4) and (4, –4)
- (4, 9) and (6, –1)
- (0, 0) and (4, –5)
- (0, –3) and (–5, –3)
Show/Hide Answer
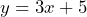
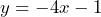
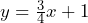
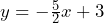
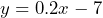
- 4
- 10
- 1
- 3/2
- 1
- 4/3
- –4
- –5
- –5/4
- 0
- https://www.nps.gov/yell/learn/nature/wolves.htm ↵

