CHAPTER 6: LINEAR GROWTH
6-1: Linear Patterns
Patterns
A pattern is a regularity in the world, in human-made design, or in abstract ideas, where the elements of a pattern repeat in a predictable manner. Patterns have an underlying mathematical structure, and recognizing patterns is a tool used in mathematics to help us create models of the world around us. Many patterns can be visualized while others require computers to recognize them.
 |
 |
 |
 |
| Sunflower with spiral pattern | Wallpaper with repeated pattern | Tiles with repeated pattern | Peacock with symmetry |
|---|
The one thing all patterns have in common is that there is a repeated element. Consider the sequence of numbers {1, 1, 2, 3, 5, 8, 13, 21, 34, 55, … }. Do you see the pattern? This sequence of numbers is called the Fibonacci sequence in which each number is the sum of the two preceding ones. The Fibonacci numbers were first described in Indian mathematics before 200 BCE. They were named after the Italian mathematician Leonardo of Pisa, also known as Fibonacci, who introduced the sequence to Western European mathematics in 1202. Fibonacci numbers appear in nature underlying spiral formations like the sunflower or the nautilus shell. The set of even numbers, {2, 4, 6, 8, …} is a pattern where 2 is added to the previous number. The set {0, 1, 4, 9, 16, 25, 36, 49, …} is the set of perfect squares, i.e. {02, 12, 22, 32, 42, 52, 62, 72,…}. The set ![]() is the set of reciprocals of the natural numbers.
is the set of reciprocals of the natural numbers.
The world is full of patterns. Some are very complicated while others are relatively simple. Being able to recognize a type of pattern in math can lead us to graphs and equations that can be used to solve problems.
 Positive Linear Patterns
Positive Linear Patterns
A positive linear pattern means that a variable amount increases by a constant amount as another variable quantity increases by a constant amount.
Explore 1 – Unit rate as a linear pattern
Chiming and his friends went to a local summer festival. They saw a sign advertising water for $2 / bottle.
- Complete the table:
Number of bottles 1 2 3 4 5 Price ($) 2
Solution
Each bottle costs $2. So, 2 bottles cost 2 · $2 = $4; 3 bottles cost 2 · $2 = $6; 4 bottles cost 4 · $2 = $8; 5 bottles cost 5 · $2 = $10.
| Number of bottles | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| Price ($) | 2 | 4 | 6 | 8 | 10 |
- Describe the pattern formed by price as the number of bottles increases?
Solution
The pattern is 2, 4, 6, 8, 10. To get from one number to the next in the sequence, we add 2. Each time the number of bottles increases by 1, the price increases by $2.
- What is the unit rate for the price of water per bottle?
Solution
At any data point in the table, the unit rate is found by dividing the price by the number of bottles. ![]() . Unit rate = $2 per bottle.
. Unit rate = $2 per bottle.
- How does the unit rate relate to the pattern you found?
Solution
The unit rate of $2 per bottle is exactly the pattern of price increase for every extra bottle.
Explore 2 – Unit rate as a linear pattern
The population of a small town increased over the few months as shown in the table.
| Month | March | April | May | June | July |
|---|---|---|---|---|---|
| Population | 500 | 520 | 540 | 560 | 580 |
- Describe the pattern formed by the population numbers in the table as the month increases.
Solution
The pattern is 500, 520, 540, 560, 580. To get from one number to the next number in the sequence, we add 20. The population increases by 20 people each month.
- What is the unit rate of population increase per month?
Solution
Unit rate of population increase per month = 20 people per month.
- How does the unit rate of population increase relate to the pattern you found?
Solution
The unit rate of population increase is 20 people per month, and the pattern of adding 20 people each month are identical.
A linear pattern is formed when there is a constant rate of increase of one variable in terms of another variable. The same amount is added each time to one variable as the other variable amount increases by another constant. In Explore 1, the constant rate of change was $2 per bottle, so the price increased by a constant amount of $2 for each increase of 1 bottle. In Explore 2, the constant rate of change was 20 people per month so, the population increased by a constant amount of 20 people for each increase of 1 month in time.
Example– Rate as a linear pattern
Gabrielle is shopping in a store where a sign is advertising $3 for any 5 items.
- Complete the table.
No. of Items 5 10 15 20 25 Cost ($) 3 - Describe the pattern of cost with respect to the increase in items.
- Determine the rate of cost per item.
- How does the rate relate to the pattern you found?
- Does the table illustrate a linear pattern?
Show/Hide Answer
-
No. of Items 5 10 15 20 25 Cost ($) 3 6 9 12 15 - The pattern is 3, 6, 9, 12, 15. To get from one number to the next number in the sequence, we add 3. The price increases by $3 as the number of items increases by 5.
- The rate at any data point is the same:
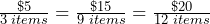 . Rate = $3 per 5 items.
. Rate = $3 per 5 items. - The rate of $3 per 5 items is identical to the pattern add $3 for every increase of 5 items.
- Since the rate of change is constant ($3 is added for every increase in 5 items) the table does illustrate a linear pattern.

- What is the relationship between rate or unit rate and a linear pattern?
Show/Hide Answer
They are identical. The rate of increase is identical to adding a constant to get from one data point to the next.
- Define in words a positive linear pattern.
Show/Hide Answer
A positive linear pattern has a repeat of a constant positive amount being added to the previous amount. The constant amount added per unit is the same as the unit rate of change.
 Negative Linear Patterns
Negative Linear Patterns
A negative linear pattern means the quantity of one variable decreases by a constant amount as the other variable amount increases by a constant. For example, if a rate of change of temperature by time is –2°F per hour, the temperature drops 2 degrees Fahrenheit every hour. The variable temperature decreases by a constant 2 degrees as the other variable, time, increases by a constant 1 hour. It is called a negative linear pattern because we add a negative number (–2°F) every hour.
Explore 3 – Negative unit rate as a linear pattern
A doctor gives a patient 24 pills to treat the symptoms they are experiencing. The table shows the remaining number of pills each day.
| Day | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| Number of Pills | 24 | 21 | 18 | 15 | 12 |
- Describe the number of pills in terms of the concept of linear pattern.
Solution
The pattern is 24, 21, 18, 15, 12 where the next number in the sequence is found by subtracting 3 (or adding –3) from the previous number. The number of pills decreases by 3 each day.
- Calculate the rate of change per day. How does this relate to the pattern you found?
Solution
Rate of change = –3 pill per day. The rate and the pattern are identical.
A constant rate of change of one variable in terms of another variable results in a linear pattern. When this rate is negative, the linear pattern is negative, so the same amount is subtracted each time from one variable as the other variable amount increases by a constant.
Explore 4 – Negative rate as a linear pattern
Danny recorded the change of temperatures every three hours in the past 12 hours since the forecast predicted a large drop in temperature. The recorded data is show in the table.
| Time | 8am | 11am | 2pm | 5pm | 8pm |
|---|---|---|---|---|---|
| Temperature (°F) | 52 | 47 | 42 | 37 | 32 |
- Describe the change in temperature in terms of time.
Solution
47 – 52 = –5; 42 – 47 = –5; 37 – 42 = –5 etc. The temperature drops by 5 degrees every three hours.
- Calculate the rate of change in temperature per hour. How does this relate to the pattern you found?
Solution
Rate = –5°F/3 hours. The rate and the pattern are identical.

- In your own words, what is a linear pattern? Write one situation in your own life that can be represented by a linear pattern.
Show/Hide Answer
A linear pattern is an increase or decrease by a constant amount every unit increase in the other amount and is equivalent to a constant rate of change. A possible situation is an increase every paycheck of a constant amount into a savings account.
Practice Exercises
- Ground beef is on sale today for $4.99 per pound. a) Complete the table. b) Describe the pattern of the price as the weight increases by 1 lb. c) What is the unit rate of change of price by weight? d) Is this a linear pattern? Explain your reasoning.
| Weight (lb.) | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| Price ($) | 4.99 |
- Lana puts away $100 every month to save for her yearly vacation. a) Complete the table. b) Describe the pattern of the total amount she has saved by month. c) What is the unit rate of change by month? d) Is this a linear pattern? Explain your reasoning.
| Month | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| Savings ($) | 100 |
- Karen posted on Instagram for a week and documented the number of likes received per post, as well as the corresponding feelings of rejection on a scale of 1 to 10 for each day. The data is presented below:
| Likes per post | 21 | 26 | 31 | 36 | 41 | 46 | 51 |
|---|---|---|---|---|---|---|---|
| Feelings of Rejection | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
- a) Describe the trend observed in the number of likes per post as feelings of rejection decrease by one each day during the week.
- b) Calculate the rate of change in the number of likes per post as feelings of rejection drop by one each day.
- c) How does this rate demonstrate the weekly negative linear pattern between likes per post and feelings of rejection?
Show/Hide Answer
- a)
Weight (lb.) 1 2 3 4 5 Price ($) 4.99 9.98 14.97 19.96 24.95 b) Add $4.99 to the price for every 1 lb increase in weight. c) $4.99 per pound d) Yes. The rate of change is constant at $4.99 per pound.
- a)
Month 1 2 3 4 5 Savings ($) 100 200 300 400 500 b) Add $100 to savings every month. c) $100 per month d) Yes. The rate of change is constant at $100 per month.
- a) As likes increase by 5 each day, feelings of rejection decrease by 1. b) –5/1 c) The decrease in feelings of rejection accounts for the negative value.
 Rates and Linear Patterns
Rates and Linear Patterns
Since a linear pattern implies a constant rate of change, we may convert a table of values with a linear pattern into a rate or unit rate. As we learned in chapter 3, the numerator is dependent upon the denominator. With data in a table, we need to determine which row represents the independent variable and which row represents the dependent variable. The value of the dependent variable will be on the numerator of the rate, while the value of the independent variable will be on the denominator of the rate. The value of the independent variable determines the value of the dependent variable.
Explore 5 – Determining a rate of change from a table
The following table shows the time and distance traveled by a car.
| Time (hours) | 3 | 6 | 9 | 12 | 15 |
|---|---|---|---|---|---|
| Distance (miles) | 180 | 360 | 540 | 720 | 900 |
- Does this table show a linear pattern? Explain your reasoning.
Solution
Yes. Every 3 hours the distance increases by a constant amount of 180 miles.
- Determine the independent and dependent variables. Explain your reasoning.
Solution
The distance traveled is dependent upon the amount of time that has passed Therefore, the dependent variable is distance, and the independent variable is time.
- Determine the rate of change shown on the table. Explain how you did it.
Solution
Since the dependent values are the distances, these go on the numerator of the rate of change. The rate is ![]() or 60 miles per hour.
or 60 miles per hour.
Explore 6 – Determining a rate of change from a table
The table shows the population of an endangered animal from 2010 to 2014.
| Year | 2010 | 2011 | 2012 | 2013 | 2014 |
|---|---|---|---|---|---|
| Population | 1000 | 940 | 880 | 820 | 760 |
- Does this table show a linear pattern? Explain your reasoning.
Solution
Yes. The population decreases by 60 every year.
- Determine the independent and dependent variables. Explain your reasoning.
Solution
The population is dependent on the year. Time is always independent as time is ongoing and depends on nothing, so the year is the independent variable. The population is the dependent variable.
- Determine the rate of change shown in the table. Explain how you did it.
Solution
The population decreases by 60 as the number of years increases. Since the population is the dependent variable, it goes on the numerator. Therefore, the rate is ![]() or –60 animals per year.
or –60 animals per year.

- Is it true that data from every table can be turned into a constant rate of change? Explain your reasoning.
Show/Hide Answer
No. A table that does not show a linear pattern cannot be turned into a constant rate. A constant rate of change is representative of a linear pattern. Only tables with a linear pattern will have a constant rate of change.
Practice Exercises
- The table shows the length of a pencil along with the turns on a pencil sharpener.
No. of turns 5 10 15 20 25 Length (cm) 10 9.5 9 8.5 8 - a) Does the table show a linear pattern? Explain your reasoning.
- b) Determine the independent and dependent variables.
- c) Determine the rate of change.
- The table shows the height of a bamboo plant along with the age of the plant.
Age 1 2 3 4 5 Height (inches) 12 30 48 66 84 - a) Does the table show a linear pattern? Explain your reasoning.
- b) Determine the independent and dependent variables.
- c) Determine the rate of change.
Show/Hide Answer
- a) Yes. There is a constant decrease in length of 0.5 cm for a constant increase of 5 turns. b) Independent = number of turns; dependent = length c) –0.5 cm for every 5 turns or –0.1 cm per turn.
- a) Yes. There is a constant increase in height of 18 inches for a constant increase in age of 1 year. b) Independent = age; dependent = height c) 18 inches per year
 In this section, we will take what we have learned and apply the concepts to new situations.
In this section, we will take what we have learned and apply the concepts to new situations.
Perspectives
- The perimeter,
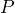 , of a square is calculated by the equation
, of a square is calculated by the equation 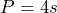 , where
, where  is the length of the side of the square. a) Find the perimeter of a square that has side-lengths of 1 cm. b) Find the perimeter of a square that has a side-length of 2 cm. c) Find the perimeter of a square that has a side-length of 3. d) What happens to the perimeter as the side-length increases by 1? e) Explain whether or not you think this pattern is linear. f) Determine the dependent and independent variables. g) Determine the rate of change.
is the length of the side of the square. a) Find the perimeter of a square that has side-lengths of 1 cm. b) Find the perimeter of a square that has a side-length of 2 cm. c) Find the perimeter of a square that has a side-length of 3. d) What happens to the perimeter as the side-length increases by 1? e) Explain whether or not you think this pattern is linear. f) Determine the dependent and independent variables. g) Determine the rate of change. - A drug that is used to prevent strokes is given to a patient based on their body weight. A 124 lb. patient was given 231 mg. A 125 lb. patient was given 231.2mg. A 126 lb. patient was given 231.4mg. a) How much more of the drug was given to the 125 lb. patient than the 124 lb. patient? b) How much more of the drug was given to the 126 lb. patient than the 125 lb patient? c) Explain whether or not you think this pattern is linear. d) Calculate the rate of change in the amount of drug given per body weight. e) If the pattern continues, how much of the drug should be given to a 130 lb. patient?
- The maximum length of wood required to frame a picture is given in the table, along with the longest side-length of the picture:
Side-length (ft) 1 2 3 4 Length (ft) 6 10 14 18 - a) Is this representative of a linear pattern? Explain your reasoning.
- b) Determine the dependent and independent variables.
- c) Determine the rate of change.
- d) What is the maximum length of wood required to frame a piece of art with a longest side-length of 6 feet?
- e) What is the maximum length of wood required to frame a piece of art with a longest side-length of 2.5 feet?
- Anthropologists may use a table to determine a person’s height based on the length of their skeleton’s femur:
Femur (in) 8 10 12 14 16 18 20 22 24 Height (in) 47.04 50.80 54.56 58.32 62.08 65.84 69.60 73.36 77.12 a) Is this representative of a linear pattern? Explain your reasoning. b) Determine the dependent and independent variables. c) Determine the rate of change. d) Determine the height of a person whose femur measures 15 inches. e) Determine the height of a person whose femur measures 21 inches.
Show/Hide Answer
- a) 4cm b) 8 cm c) 12cm d) As the side-length increases by 1cm, the perimeter increases by 4cm e) Yes. There is a constant increase of 4cm in perimeter for every constant 1cm increase in side-length. f) Dependent = perimeter; independent = side-length g) 4cm per 1cm or 4.
- a) 0.2mg b) 0.2mg c) Yes. The drug amount increases by a constant of 0.2mg for every 1 lb. increase in patient weight. d) Rate = 0.2mg per pound e) 232.2mg
- a) Yes. The side-length increases by a constant of 1 ft while the length increases by a constant 4 ft. b) dependent = length; independent = side-length c) Rate = 4ft/1ft = 4 d) 22 ft e) 12 ft
- a) Yes. There is a constant increase of 3.76 in height and a constant increase of 2 inches in femur length. b) dependent = height; independent = femur length c) Rate = 3.76 in/2 in = 1.88 d) 60.20 in. e) 71.48 in.
 In this section, we will use what we have learned so far to practice skill problems.
In this section, we will use what we have learned so far to practice skill problems.
Skill Exercises
Determine the linear pattern:
- 3, 6, 9, 12, 15
- 7, 3, –1, –5, –9
- 0, 4, 8, 12, 16
- 9, 2, –5, –12, –19
- 3.4, 3.7, 4.0, 4.3
- –4.5, –4.7, –4.9, –5.1, –5.3
- 34.5, 4.5, –25.5, –55.5
- 99.5, 99.2, 89.9, 89.6, 89.3
- –4, –5.1, –6.2, –7.3, –8.4
- 3/4, 1, 5/4, 3/2, 7/4, 2
State the dependent variable then determine the constant rate of change:
-
Weight (kg) 2 4 6 8 10 Price ($) 12.50 25.00 37.50 50.00 62.50 -
Price ($) 4.99 8.98 12.97 16.96 20.95 Length (cm) 1cm 2cm 3cm 4cm 5cm -
Perimeter (ft) 9 21 33 45 57 Side-length (ft) 3 7 11 15 19 -
Speed (mph) 4 19 34 49 64 Time (sec) 1 3 5 7 9 -
Time (sec) 4 8 12 16 20 Length (m) 0.2 0.7 1.2 1.7 2.2
Show/Hide Answer
- Add 3
- Subtract 4 or add –4
- Add 4
- Subtract 7 or add –7
- Add 0.3
- Subtract 0.2 or add –0.2
- Subtract 30 or add –30
- Subtract 0.3 or add –0.3
- Subtract 1.1 or add –1.1
- Add 1/4
- Price. $6.25 per kg
- Price. $3.99 per cm
- Perimeter. 3
- Speed. 7.5 mph per second
- Length. 0.3m/4 sec or 0.075 meters per second
the variable that has values that have no dependency on any other variable(s)
a variables whose values are tied to the value of another variable

