5-2: Equations and Solutions

Hazel McKenna; Leo Chang; Roxanne Brinkerhoff

CHAPTER 5: LINEAR EQUATIONS IN ONE VARIABLE

5-2: Equations and Solutions

Introduction

Equations provide a very precise way to describe various features of the world around us. In reality, most equations arising from real world contexts cannot be solved algebraically. Rather computers are employed to determine numerical solutions to such problems, if they can be found. But there are some equations that can be solved without the use of a computer and the exercise of determining solutions for such equations is possible the best way to become competent at understanding what the equation is telling us.

Equations and Solutions

An equation is a statement that two mathematical expressions are equal. An equation can be numerical (e.g., 8 = 8 or 3 + 5 = 6 + 2) or it can be algebraic (e.g., $2x-3=7$ . An equation that is always true (e.g., 7 + 1 = 8 or $6x=4x+2x$ ) is called an identity. An equation that is never true (e.g., 4 + 3 = 9) is called a contradiction. The most interesting equations are those that are sometimes true. Such equations are called conditional equations. For example, $x+2=5$ is only true when $x=3$ . It is not true for any other value of $x$ . $x=3$ is called the solution of the equation. Some equations, like $x+2=5$ have only one solution (i.e., $x=3$ ), while other equations have more than one solution. For example, the equation $x^2=4$ has two solutions, $x=2$ (since 2² = 4) and $x=-2$ (since (–2)² = 4).

Explore 1 – Translate a problem into an equation

In a store, the price of a pair of pants is three times the price of a t-shirt.

If the price of a t-shirt is $x$ , write the price of a pair of pants in terms of the price of the t-shirt.

Solution

Since the price of a t-shirt is $x$ and the price of a pair of pants is three times of the price of a t-shirt, the price of a pair of pants is $3x$ .

Write an expression in terms of $x$ that shows the cost if you buy 4 pairs of pants and 3 t-shirts. Simplify the expression.

Solution

The cost of buying 4 pairs of pants and 3 t-shirts = $4(3x) + 3x=12x+3x=15x$

If the cost of buying 4 pairs of pants and 3 t-shirts is $349.95, write an equation to show this.

Solution

We already know that the cost is $15x$ , so if the cost is also $349.95, then $15x=\$349.95$ .

Example

During a traditional Mexican festival, Enola and Malia visit a food stall to buy tacos and beverages. Enola purchases 3 tacos and a $6 Jarritos soda, while Malia buys 4 tacos. They compare their receipts and discover that they both spent the same amount on their purchases.

Using 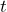$t$ to represent the cost of a taco, write an expression that represents Enola’s purchase.
Using 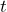$t$ to represent the cost of a taco, write an expression that represents Malia’s purchase.
Write an equation that represents their purchases and could be used to determine the price of a taco.
Why can the two expressions be set equal?

Show/Hide Answer

$3t+6$
$4t$
$3t+6=4t$
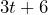
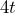
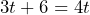
Since their receipts show the same purchase price, we can set them equal to each other.

Explore 2 – Solutions of an equation

The equation $R=np$ represents the revenue ( $R$ ) a business makes if it sells $n$ units of a product at a price of $p$ .

How many variables are in the equation?

Solution

There are 3 variables: $R,\;n,\;p$

Determine if the values 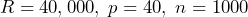$R=40,000,\;p=40,\;n=1000$ is a solution of the equation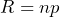 $R=np$

Solution

When $R=40,000,\;p=40,\;n=1000$ , the equation $R=np$ becomes $40,000=1000\times40$ , which simplifies to $40,000=40,000$ . This is TRUE, so $R=40,000,\;p=40,\;n=1000$ is a solution.

Determine if the values 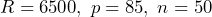$R=6500,\;p=85,\;n=50$ is a solution of the equation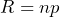 $R=np$

Solution

When $R=6500,\;p=85,\;n=50$ , the equation $R=np$ becomes $6500=50\times85$ , which simplifies to $6500=4250$ . This is FALSE, so $R=6500,\;p=85,\;n=50$ is NOT a solution.

What does the symbol $=$ mean? When is it used?

Show/Hide Answer

The symbol $=$ means equals or equal to. It is used to show that two expressions are equal. The two expressions can be numerical or algebraic.

Explain the difference between an expression and an equation.

Show/Hide Answer

An expression is a mathematical statement (e.g., $6x+3y-9$ ), while an equation is two expressions set equal to one another (e.g., $6x+3y-9=5x+8$ .

Explain how to determine if given values are a solution of an equation.

Show/Hide Answer

Substitute each variable with its given value and simplify the equation. If the equation is true, the values are a solution. If the equation is fase, the values are not a solution.

Practice Exercises

Jasmine ordered 24 small cups online. She received the cups in 6 boxes. Each box has the same number of cups. Jasmine just learned about equations recently and wants to use the concept to represent the relationship of the 24 cups in the 6 boxes. Suppose Jasmine uses the letter 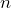$n$ to represent the number of cups in each box. Write an equation to represent the relationship of the 24 cups in the 6 boxes.
Tickets go on sale tomorrow for a rock concert. Each ticket costs $75 and there is a convenience fee to buy them online of $20. Suppose Carli buys 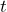$t$ tickets online. Write an equation that represents the cost, 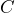$C$ of the tickets.
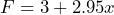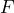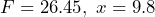The equation $F=3+2.95x$ represents a taxi fare, $F$ , for a taxi ride of $x$ miles. a) Determine if $F=26.45,\;x=9.8$ is a solution of the equation. b) Determine if 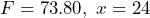$F=73.80,\;x=24$ is a solution of the equation.
Working as a car salesman, Ricky earns a commission of 3% of the sale price on every car he sells. The equation 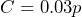$C=0.03p$ represents his commission, 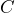$C$ on a car sales of 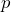$p$ . a) Determine if 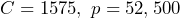$C=1575,\;p=52,500$ is a solution of the equation. b) If Ricky sells a total of $236,450 in car sales this month, how much commission will he earn?

Show/Hide Answer

$6n=24$
$C=75x+20$
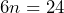
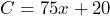
a) No b) Yes
a) Yes b) $7093.50

Linear Equations in One Variable

An equation is said to be an equation in one variable when it has exactly one variable (e.g., $x$ ). Examples of an equation in one variable are $3x^2-7=3x+4$ and $8x+9=2(3x-5)$ . Each equation contains the single variable $x$ .

An equation in one variable is said to be linear when the highest exponent on the variable is 1 (e.g., $x^1$ which is written $x$ ). Examples of a linear equation in one variable are $6x=-18$ and $8x+9=2(3x-5)$ . Each equation contains the single variable $x$ whose highest exponent is 1.

Explore 3 – Identifying linear equations in one variable

Determine which of the equations are linear equations in one variable:

$4x^3-7x=9$

Solution: Although there is only one variable, the highest exponent is 3 so it is not linear.

$7x+8=4$

Solution: There is only one variable, and the highest exponent is 1 so it is a linear equation in one variable.

$3x-6y=8$

Solution: There are 2 variables ( $x$ and $y$ ) so it is not a linear equation in one variable. The highest exponent on either variable is 1 so it is a linear equation in 2 variables, which we will study in the next chapter.

$4(3x-7)=7x+9$

Solution: There is only one variable, and the highest exponent is 1 so it is a linear equation in one variable.

Explore 4 – Solutions of linear equations in one variable

The equation $R=nx$ represents the revenue ( $R$ ) a business makes if it sells $n$ units of a product at a price of $x$ . If we know that the revenue was $65,000 when 5000 units were sold, then the equation becomes $65,000=5000x$ , which is a linear equation in one variable.

Determine which of the following is a solution of the equation:

A) $x=30$ B) $x=10$ C) $x=13$ D) $x=15$

Solution

When $x=30$ , the equation $65,000=5000x$ becomes $65,000=5000\times30$ , which simplifies to $65,000=150,000$ . This is false, so $x=30$ is NOT a solution.

When $x=10$ , the equation $65,000=5000x$ becomes $65,000=5000\times10$ , which simplifies to $65,000=50,000$ . This is false, so $x=10$ is NOT a solution.

When $x=13$ , the equation $65,000=5000x$ becomes $65,000=5000\times13$ , which simplifies to $65,000=65,000$ . This is true, so $x=13$ is a solution.

When $x=15$ , the equation $65,000=5000x$ becomes $65,000=5000\times15$ , which simplifies to $65,000=75,000$ . This is false, so $x=30$ is NOT a solution.

We could have stopped checking after determining that $x=13$ is a solution of the equation, because conditional linear equations in one variable have exactly one solution.

Reflect Icon

What is the definition of a linear equation in one variable?

Show/Hide Answer

A linear equation in one variable when it has only one variable and the highest exponent on the variable is 1.

Practice Exercises

Determine which of the equations are linear equations in one variable. If the answer is no, say why it is no.

$3x-7=9$
$4x-7=6y-3$
$x^2=3x+4=0$
$5=3x-6$
$2xy-3-x+y$
$7(3x-8)+2=-4x+5$
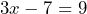
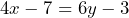
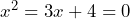
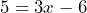
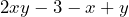
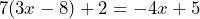
Suppose that in a game of poker each white chip is worth 1/2 of a green chip. a) Write an equation that represents the value of a green chip, 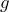$g$ , in terms of the value of a white chip, 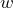$w$ . b) If a white chip is worth $10, what is the value of a green chip?
The distance in miles a car can travel is the number of gallons the gas tank holds times the number of miles per gallon the car is rated at. Suppose a car gets 25 mpg, {latex]g[/latex] is the number of gallons of gas in the tank, and 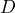$D$ is the distance the car can travel. a) Write an equation to represent the distance the car can travel in terms of 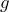$g$ . b) What distance can the car travel if the gas tank is full? c) What distance can the car travel if there are 5 gallons in the tank?

Show/Hide Answer

Yes.
No: 2 variables
No: highest exponent is 2
Yes
No: 2 variables
Yes
a) 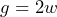$g=2w$ b) $20
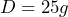a) $D=25g$ b) 625 miles c) 125 miles

In this section, we will take what we have learned and apply the concepts to new situations.

Perspectives

1. The total cost of an item is the price of the item plus tax. The tax can be found by multiplying the price by the tax rate. Suppose the tax rate is 6.8%, $p$ is the price of the item, and $C$ is the total cost of the item.

a) Write an equation that represents the total cost of an item in terms of the price, then simplify it.

b) What percent of the price of the item is the total cost?

c) Use the equation to determine the total cost of buying an item whose price is $85.99.

d) Use the equation to determine the total cost of buying an item whose price is $5.99.

2. The price after a discount has been applied is the original price minus the discount. The discount can be found by multiplying the price by the discount rate. A store is advertising 20% off everything it sells. Suppose $p$ is the original price of an item and $C$ is the cost after the discount has been taken.

a) Write an equation that represents the discount price in terms of the original price, then simplify it.

b) What percent of the original price will the item cost you?

c) Use the equation to determine the discount price of an item whose original price is $85.99.

d) Use the equation to determine the discount price of an item whose original price is $349.99.

3. The cost of household electricity can be found by evaluating the expression $C=[(R - R_1) \cdot E + B] \times(1+T)$ , where $C=$ cost, $R =$ current meter reading; $R_1 =$ previous meter reading; $B =$ basic charge; $E =$ energy charge per kWh; and $T =$ tax rate. Since $B=8,\;E=0.0821260$ and $T=10.9%$ are constants, the equation can be rewritten as $C=[(R - R_1)\times 0.0821260 + 8] \times(1+0.109)$ , which simplifies to $[(R - R_1)\times 0.0821260 + 8] \times 1.109$ .

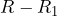a) If $R - R_1$ is defined to be $x$ and we know the total cost is $65.34, write the equation that could be used to determine the value of $x$ .

b) Is the equation in part a) a linear equation in one variable?

c) Determine if 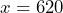$x=620$ is a solution of the equation.

d) Determine the current meter reading if the previous meter reading was 32,760.

4. As a salesperson Pat earns a base wage plus 0.5% commission on the sales price of every item sold. The equation $W=B+0.005x$ represents Pat’s total wage, $W$ , based on a base wage, $B$ , and total sales worth $x$ .

a) If Pat’s base wage is $40,000 and their total wage last year was $84,650, write the equation that represents this situation and determine if it is a linear equation in one variable.

b) Determine if 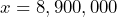$x=8,900,000$ is a solution of the equation in part a)

c) Determine if 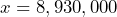$x=8,930,000$ is a solution of the equation in part a)

Show/Hide Answer

a) 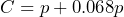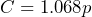$C=p+0.068p$ ; $C=1.068p$ b) 106.8% c) $91.84 d) $6.40
a) 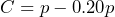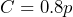$C=p-0.20p$ ; $C=0.8p$ b) 80% c) $68.79 d) $279.99
a) 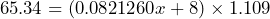$65.34=(0.0821260x + 8) \times 1.109$ b) Yes c) Yes d) 33,380
a) 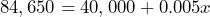$84,650=40,000+0.005x$ Yes, this equation is linear in one variable. b) No c) Yes