CHAPTER 4: DATA MEASUREMENT

4-2: Weighted Means

Introduction

The mean of a set of data is calculated by adding up all the data point values then dividing the sum by the total number of data points. This assumes that each data point has the same worth. But this is not always the case. Weighted mean is a calculation that considers the varying degrees of importance of the numbers in a data set. It is commonly used to find grade point averages where each course has a different weight (e.g., the number of credits). Stock investors use a weighted mean to track the cost basis of shares bought at varying times. In a weighted mean, each data point value is multiplied by the assigned weight which is then summed and divided by the sum of weights. A weighted mean reflects the relative importance of each observation and is thus more descriptive than a simple mean.

Explore Icon Calculating a Weighted Mean

When data points are assigned different weights, we use a weighted mean to determine the average of the data set. The mean that we explored in the previous section is a special case of the weighted mean where every weight is equal to one. Weighted means take into account not just the quantity of data points but also their relative importance.

Explore 1 – Calculating the weighted mean

Grade Point Average (GPA) is a weighted mean, weighted by the number of credits a course has assigned to it. It converts letter grades earned in a course into a numerical scale where A = 4.0; A– = 3.7; B+ = 3.4; B = 3.0; B– = 2.7; C+ = 2.4; C = 2.0; C– =1.7; D+ = 1.4; D = 1.0; D– = 0.7; E = 0. These numbers get multiplied by the number of credits for the course in which they were earned, summed, then divided by the total number of credits taken.

Calculate the GPA of a student who earned an A in English (3 credits); a B+ in Racquetball (1 credit); a B in Math (4 credits); and a C– in Chemistry (3 credits).

Solution

We start by assigning a numerical value to each grade earned: A = 4.0; B+ = 3.4; B = 3.0; C– = 1.7

Now we multiply each numerical grade value by the number of credits assigned to each course to determine the weighted value of each data point:

English: 4.0\times3=12, Racquetball: 3.4\times1=3.4, Math = 4\times3.0=12, Chemistry: 1.7\times3=5.1

Then we sum the weighted values: 12 + 3.4 + 12 + 5.1 = 32.5

Finally, we divide the sum of the weighted values by the total number of weights (credits).

The total number of credits is 3 + 1 + 4 + 3 = 11, so we divide by 11: 32.5 \div 11 = 2.95\overline{45}

Since GPAs are typically given to 2 decimal places, we round the answer to 2 decimal places: 2.95

The student’s GPA is 2.95.

 

As a single calculation,

    \[\begin{split}GPA &= \dfrac{4\times3+3.4\times1+3\times4+1.7\times3}{3+1+4+3}\\&=\dfrac{32.5}{11}\\&\approx2.95\end{split}\]

 

Weighted means are useful when we want to give more importance to certain values than others. In the case of GPA, the weights are the number of credit hours per course. This means that a course with a higher number of credit hours is given more importance than a course with fewer credit hours. In Explore 1, Math has 4 credit hours while Racquetball has only 1 credit hour. As far as GPA is concerned, Math is 4 times more important than Racquetball, so the grade earned in Math counts more than the grade earned in Racquetball.

 

Weighted Mean

  • Calculate the weighted value of each data point by multiplying each data point value by its weight
  • Sum the weighted values by adding the weighted value of each data point
  • Divide the sum by the sum of the weights for each data point

 

 Weighted \;mean =\dfrac{Sum\;of\;(data\;point\times weight)}{Sum\;of\;weights}

 

Explore 2 – Calculating the weighted mean

On a survey conducted among 100 individuals, they were asked to rate their belief in the existence of global warming on a scale of 1 to 5, with 5 representing strong belief and 1 representing no belief. The results of the survey are as follows:

Strong Belief (5): 30 individuals

Moderate Belief (4): 25 individuals

Neutral (3): 15 individuals

Skeptical (2): 20 individuals

No Belief (1): 10 individuals

Calculate the weighted mean belief score on global warming based on the survey results, then explain what the weighted average tells us.

Solution

\begin{aligned}\text{Weighted mean belief score}&=\dfrac{\text{Sum of (data point}\times \text{weight)}}{\text{Sum of weights}}\\\\ &= \dfrac{5(30)+4(25)+3(15)+2(20)+1(10)}{100}\\&=3.45\end{aligned}

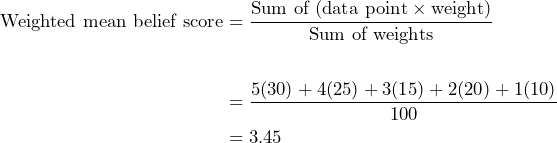
This tells us that of the individuals who took the survey, they average between neutral to a moderate belief in the existence of global warming.

 

 

Explore 3 – Calculating the weighted mean

Janet is trying to calculate her final grade in a class. The weights for each grading category and her grades are listed below. Calculate Janet’s final grade.

Category Homework Chapter Tests Attendance Midterm Exam Final Exam
Weight 30% 20% 10% 15% 25%
Grade 95 78 90 75 80

Solution

The weights are the percentage of the overall grade that each category counts towards. Homework with a weight of 30% counts the most, followed by the final exam with a weight of 25%.

    \[\begin{split}\text{Weighted mean} &=\dfrac{\text{Sum of (data point}\times \text{weight)}}{\text{Sum of weights}}\\\\&=\dfrac{30\%\times 95+20\%\times 78+10\%\times 90+15\%\times 75+25\%\times 80}{30\%+20\%+10\%+15\%+25\%}\\\\&=\dfrac{8435\%}{100\%}\\\\&=84.35\end{split}\]

Janet’s grade is 84.35

 

Examples

  1. You bought shares in Apple at three different times over the last 10 years. First you bought 200 shares at $13.61 per share, then a couple of years later you bought 100 shares at $18.94 per share, and finally you bought 150 shares at $38.07 per share. Calculate the weighted average price per share.
  2. Matt wants to calculate his semester’s GPA before the official University transcript comes out. He earned an A in a 4-credit Math course; a C+ in a 3-credit Philosophy course; a B+ in a 3-credit History course; and an A– in a 1-credit PE course. a) Calculate Matt’s GPA.     b) Matt gets a shock when his official GPA comes out as it is not what he calculated. Matt has forgotten to officially withdraw from a 4-credit hour Spanish course. Consequently, he earned a grade of UW for this course, which comes with a weight of 0 towards his GPA. Calculate Matt’s official GPA. The letter grades earned in a course are converted into a numerical scale where A = 4.0; A– = 3.7; B+ = 3.4; B = 3.0; B– = 2.7; C+ = 2.4; C = 2.0; C– =1.7; D+ = 1.4; D = 1.0; D– = 0.7; E = 0; UW = 0.

 

Show/Hide Answer

  1. Weighted average price per share = \dfrac{\$13.61 (200) + \$18.94(100) + \$38.07 (150)}{200 + 100 + 150} = \$19.16

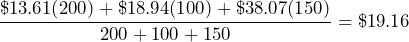
  2. a) GPA = \dfrac{4(4)+1.7(3)+3.4(3)+3.7(1)}{4+3+3+1}=3.37

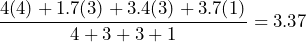
b) GPA = \dfrac{4(4)+1.7(3)+3.4(3)+3.7(1)+0(4)}{4+3+3+1+4}=2.47

 

Reflect Icon

 

  • What is “weight”? What is the “weighted value of a data point”? What is a “weighted mean”?
Show/Hide Answer

The weight of a data point shows how important the data point is compared to the weights of the other data points. It shows the magnitude of enlargement (if the weight is greater than 1) of a data point value. The weighted value of a data point means the value of a data point is multiplied by its weight. A weighted mean is the mean of the weighted values of the data points (i.e., sum of the weighted values divided by the total weight).

  • Jose claims that weights do not have to be whole numbers. Weights can even be less than 1. Do you agree?
Show/Hide Answer

Jose’s claim is correct. The weights are relative to each other, so weights for 4 categories that are 3, 2, 2, 1 with a sum of 8 could just as easily be written as 0.3, 0.2, 0.2, 0.1 with a total of 0.8. The ratio between any two weights remains the same.

 

Practice Exercises

  1. Braidy wants to calculate her semester’s GPA before the official University transcript comes out. She earned an B+ in a 4-credit Math course; a C in a 3-credit English course; a B– in a 3-credit French course; and an B+ in a 1-credit PE course. a) Calculate Braidy’s GPA. b) Braidy gets a shock when her official GPA comes out as it is not what she calculated. Braidy has forgotten to officially withdraw from a 3-credit hour Biology course. Consequently, she earned a grade of UW for this course, which comes with a weight of 0 towards her GPA. Calculate Braidy’s official GPA. The letter grades earned in a course are converted into a numerical scale where A = 4.0; A– = 3.7; B+ = 3.4; B = 3.0; B– = 2.7; C+ = 2.4; C = 2.0; C– =1.7; D+ = 1.4; D = 1.0; D– = 0.7; E = 0; UW = 0.
  2. Kim is responsible for hiring a new employee. Over 500 candidates have applied for the job so Kim has created a rubric to help rank the candidates. The top nine candidates are shown in the table. Calculate a weighted average for each candidate then rank them in order from highest to lowest.
Category Weight (%) Candidate A Candidate B Candidate C Candidate D Candidate E Candidate F Candidate G Candidate H
Qualifications 40 5 5 5 5 5 4 4 4
Working Skills 30 4 4 5 3 5 5 4 5
Team Work 20 3 4 3 1 3 2 5 3
Personality 10 5 3 4 3 4 4 2 5

 

Show/Hide Answer
  1. a) 2.83  b) 2.22
  2. A = 4.30; B = 4.30; C = 4.50; D = 3.40; E = 4.50; F = 3.90; G = 4.00; H = 4.20  From highest to lowest: C/E; A/B; H; G; F; D

 

Explore Icon Understanding the Effect of Weights in a Weighted Mean

The weighted mean of a set of data is determined by two parts, the value of each data point and the weight of each data point. If the value of each data point is the same, a larger weight of a data point will result in a larger weighted value for that data point (the data point value multiplied by the weight).

 

Explore 4 –The effect of weights in the weighted mean

Given the grading categories and weights below,

  1. Do you need to get 80 in each category to get a total score of at least 80?
  2. If you earn a final exam score of 60, is it possible that you will still pass the class? The passing grade is 73.
  3. Determine at least one other set of scores that will get you a passing grade if your final exam score is 60.
Catetory Homework Chapter Tests Attendance Midterm Exam Final Exam Total
Weight 30 20 10 15 25 100
Grade

Solutions

  1. No. For example, the total score will still be more than 80 if you earn 70 in attendance and 85 in homework and 80 in the other categories. This is because the weight of homework is three times the weight of attendance. The you drop 10 points in attendance (from 80 to 70) you need only 1/3rd of these points in homework to make up your grade (since homework counts for the 3 times the weight of attendance). So, an additional 3.33 points (i.e., 10 ÷ 3) in homework will guarantee at least 80% overall. For example, 5 additional points in homework results in 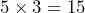5\times3=15 weighted points earned from homework towards the final grade.
  2. Yes, it is possible. A score of 60 on the final exam will have a weighted value of (25 · 60) ÷ 100 = 15 towards your grade. Your weighted score with an 80 on the final exam was (25 · 80) ÷ 100 = 20, so you have lost 20 – 15 = 5 points from your grade. To make up the 5 points would require an increase in another category. Since homework has a weight of 30, increasing homework by 30 ÷ 5 = 6 points would earn back the lost 10 points from the final exam. Alternatively, more than one category could be increased. For example, your total score will be at least 80 if you get 93 in homework, 85 in chapter tests, 80 in attendance, and 80 on the midterm exam: 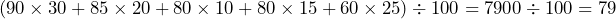(90\times30+85\times20+80\times10+80\times15+60\times25)\div100=7900\div100=79, which is a passing grade.

  3. One possible set of scores that will get you a passing grade if your final exam score is 60 is: Homework = 100, Chapter Tests = 100, Attendance = 100, and Midterm Exam = 100. With these scores, your weighted average would be 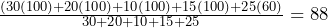\frac{(30(100) + 20 (100) + 10 (100) + 15 (100) + 25 (60)} {30 + 20 +10 +15+25} = 88, which is above the passing grade of 73.

 

Explore 5 – The effect of weights in the weighted mean

To measure the success of an NFL quarterback, the NFL uses a calculation known as the adjusted net passing yards per attempt, or ‘ANY/A’.  The formula is:

ANY/A = [passing yards + 20(number of passing touchdowns) – 45(number of interceptions thrown) – sack yards lost] ÷ (number of passing attempts + number of sacks)

Suppose an NFL quarterback has the following numbers:

Completed passes Passing attempts Passing yards Passing touchdowns Interceptions Sacks Sack yards lost
420 642 5620 58 12 15 95
  1. Calculate this players ANY/A. Round to the nearest hundredths place.
  2. What value in the formula has the greatest effect on the measure ANY/A?
  3. If this player wants to increase his ANY/A value, what should he work on? Explain your reasoning.

Solution

  1. (5620 + 20\times58 - 45\times12 - 95)\div(642 + 15)=5785\div657=8.81
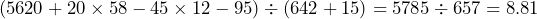
  2. The number of interceptions thrown because it has the highest weight of 45.
  3. The number of interceptions thrown has the greatest weight and it is subtracted so it counts a great deal against having a high ANY/A. The next highest weight is 20 for the category number of passing touchdowns and since it is positive it counts towards having a high ANY/A. So this player needs to stop throwing interceptions and increase the number of passing touchdowns.

 

Reflect Icon

 

  • How does a weight influence the “weighted value” of a data point?
Show/Hide Answer

The larger the weight of a data point is, the larger weighted value the data point has.

 

Practice Exercises

  1. You are responsible for shortlisting candidates for a face-to-face customer service job. You have been asked to create a rubric that will help you. What categories would you use and what weights would you assign to them? Explain your reasoning.
  2. Sandy is considering buying a new car. She has created a rubric to help her make a decision, and scores each category out of 10. a) What category has the greatest effect on the weighted mean?   b) WIthout doing any calculations, what car looks like the best choice? Explain your reasoning.   c) Calculate the weighted mean for each car. d) According to this rubric, what car should she buy?
Category Weight Car A Car B Car C Car D
Safety 30 10 9 8 8
Comfort 25 8 9 7 5
Fuel Mileage 20 5 6 8 6
Exterior looks 15 8 10 9 8
Interior looks 10 8 7 10 9
Show/Hide Answer
  1. Answers vary but may include: communication skills; personality; work ethic; qualifications; job skills
  2. a) Safety  b) Answers vary.  c) Car A = 8.00; Car B = 8.35; Car C = 8.10; Car D = 6.95  d) Car B

 

 

In this section, we will take what we have learned and apply the concepts to new situations.

Perspectives

  1. An Artificial Intelligent search engine collects each user’s Internet browsing history and codes the webpage contents with one of three levels of relevance to the user: 1 = no relevance; 2 = relevant; and 3 = very relevant. The statements in a webpage are categorized into six topics. The following are the number of statements in each category, and the codes of relevance to the user.  Calculate the weighted average relevance score (to the user) of this webpage?.
Topic A B C D E
Number of statements 18 45 20 16 37
Relevance weight 1 1 3 3 2
  1. Hoa and her friends are playing a dart game. The dartboard is divided circularly into 5 areas with the scores of 10, 8, 5, 2, 1 from the inner circle to the outer circle. Each player has ten darts. The result is shown in the following table. What is the weighted average score per dart?
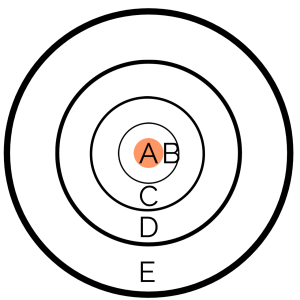
Area A B C D E
Score 10 8 5 2 1
Number of darts 1 1 3 3 2
  1. Alan is trying to determine the minimum grade he needs to earn on their final exam. The maximum score for any category is 100. a) Determine the minimum grade Alan needs to pass the class with a grade of 70 or better. b) Is it possible for Alan needs to pass the class with a grade of 80 or better? Explain your reasoning.
Category Homework Tests Projects Group work Participation Final Exam
Weight 10 20 30 10 10 20
Score 75 68 72 80 50
  1. A writer sends an invoice for her latest work. She wrote 8 blog pages for $50 each; 3 ads for $30 each; and a technical manual for $350. Calculate her wage per project.
  2. Sarah is researching phones and decides to create a weighted average to determine the ‘best’. She uses the following weights: 50% battery life, 30% cost, and 20% camera quality to calculate a score for each phone. She uses Internet based reviews to determine her ratings out of 10 for each category. Calculate the weighted average score for each phone, then determine which phone she should buy based on her ratings.
Category Battery Life Cost Camera Quality
Weight 50% 30% 20%
iPhone 9 7 9
Samsung 9 7 7
Motorola 8 9 7

 

  1. Vacancy rates measure the number of units—or the amount of square footage—that are available for occupancy at a point in time. It refers to the percentage of the stock of built space in the market that is not currently occupied. High vacancy rates are characteristics of oversupplied markets. Conversely, low vacancy rates signal that the demand for space exceeds supply of space and that there may be a need to add more space to the market.
Calculate the weighted average vacancy rate for the eight buildings detailed in the table.
Building Total leasable space (ft2) Vacancy rate (%)
B1 5400 20
B2 2800 0
B3 7500 25
B4 10,400 30
B5 8500 10
B6 12,800 35
B7 3600 10
B8 22,400 28

 

  1. A Professor published 4 articles, wrote 2 book chapters, and completed 5 conference presentations in the last 5 years. The University’s Scholarship Point Scale gives 5 points for a published article, 4 points for a published book chapter, and 2 points for a conference presentation. Find the Professor’s average for scholarship points.
  2. COVID-19 vaccines hesitancy and doubts are common among certain individuals. Some reasons for the skepticism include concerns about the rapid development and fear of potential side effects. In a survey conducted among 200 individuals, they were asked whether they would take a COVID-19 vaccine. The responses were categorized into five options: Definitely Yes, Probably Yes, Undecided, Probably No, and Definitely No. The results of the survey are as follows:

Definitely Yes (5): 100 individuals

Probably Yes (4): 50 individuals

Undecided (3): 30 individuals

Probably No (2): 15 individuals

Definitely No (1): 5 individuals

Calculate the weighted mean of the willingness to take a COVID-19 vaccine based on the survey. results.

  1. In a quality control assessment of the campus racial climate in a college, racial minority students were asked to rate their perception of the campus climate on a scale of 1 to 5, with 5 representing a positive and inclusive racial climate and 1 representing a negative and exclusionary racial climate. The results of the assessment for racial minority students are as follows:

Positive Climate (5): 25 students

Moderately Positive Climate (4): 15 students

Neutral Climate (3): 10 students

Moderately Negative Climate (2): 5 students

Negative Climate (1): 3 students

Calculate the weighted mean perception of the campus racial climate based on the assessment results from racial minority students.

Show/Hide Answer
  1. 24.5
  2. 4.1 points per dart
  3. a) 71.5  b) No. They would need a score of 121.5 or higher, which is impossible with a maximum score per category of 100.
  4. $70 per project
  5.  iPhone = 8.4; Samsung = 8.0; Motorola = 8.1    She should buy an iPhone since it has the highest weighted average.
  6. 24.6%
  7. The Professor’s average for scholarship points is 3.45
  8. Weighted mean = 4.125 and tells us that of the 200 individuals surveyed, on average they would probably or definitely take a COVID-19 vaccine.
  9. Weighted mean perception = 3.93 and tells us that of the racial minority students surveyed on average their perception is that there is a neutral to moderately positive racial climate.

 

 

Skills IconIn this section, we will use what we have learned so far to practice skill problems.

Skill Exercises

Calculate the weighted mean for the given data set:

  1. Weights 20 20 50
    Scores 65 54 78
  2. Weights 50 20 75
    Scores 40 60 50
  3. Weights 65 25 20 10 10
    Scores 20 40 30 76 85
  4. Weights 20 20 30 45 10
    Scores 38 76 45 85 92
  5. Weights 20 30 –20 –35 65
    Scores 89 76 10 15 75
Show/Hide Answer
  1. 69.78
  2. 47.93
  3. 34.69
  4. 67
  5. 136.83

 

 

definition

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

Numeracy Copyright © 2023 by Utah Valley University is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.