CHAPTER 3: RELATIVE MEASUREMENT

3-3: Percentages

Percent or Percentage?

There are 100 cents in a dollar, 100 years in a century, 100 legs on a centipede, and 100 centimeters in a meter. Cent is a Latin root and means hundred. The word percent can be broken down into two parts: per meaning for each or for every and cent meaning hundred. So, mathematically, 7 percent is 7 for every 100, or 7/100. The symbol for percent is %. For example, if a bank adds 2% interest, investors will earn $2 for every $100 invested, which simplifies to a unit rate of $0.02 = 2¢ for every dollar invested. If you leave an 18% tip on a restaurant bill, you leave $18 for every $100 spent or, as a unit rate, 18 cents for each dollar spent. Percent is always associated with a number (e.g. 10%). The % sign replaces the word percent.

Percentage is a more general term used when there is no number given. For example, there is a considerable percentage difference in ability between the two groups of students. As another example, there are a certain percentage of individuals who will disagree with everything you say. Another difference between percentage and percent, is that percentage cannot be replaced by the % sign.

Explore Icon Definition of Percent

A percent (from the Latin per centum  meaning by a hundred) is a number or ratio expressed as a fraction of 100. Since a percent is a number, it has no dimension (no measurement units) associated with it. The symbol for percent is %. So, 7% is a number equal to the fraction \dfrac{7}{100} or the decimal 0.07.

A percent is used when we want to express a relative measure, i.e. a measure based on another measure. For example, the statement “85% of the population of a city agree with a proposal” means that for every 100 people in the city, 85 people agree on the proposal. To determine exactly how many people in the city agree with the proposal, we would have to know the population of the city. If 0% of the people in the city agreed with the proposal, then no one agreed. If 100% of the population of the city agreed with the proposal then everyone agreed.

In other words, a percent is a fraction of a whole where the whole is split into 100 equal parts. The whole = 100% = 100/100 = 1 and 0% = 0/100 = 0. If the percent is greater than 100%, then there is more than one whole. For example, 200% = 100% + 100% = 2 wholes, 300% = 3 wholes, etc.

 

Explore 1 – The definition of percent

1. The Red Cross reports that, “90 cents out of every dollar” goes to their humanitarian efforts.[1] What percent does this represent?

Solution

90 cents out of every dollar can be written as the ratio \dfrac{90\;cents}{\$1}. This can then be simplified by writing $1 = 100¢ and cancelling the cents:

\begin{aligned}\dfrac{90\;cents}{\$1}&=\dfrac{90\;\cancel{cents}}{100\;\cancel{cents}}\\\\&=\dfrac{90}{100}\\\\&=90\%\end{aligned}

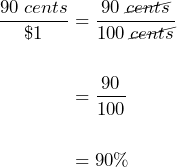
2. 37 people in a 100-person math class are NOT freshman. What percent of students in the math class are freshmen?

Solution

If 37 people are NOT freshmen, then 100 – 37 = 63 people ARE freshmen. So 63 out of 100 people are freshmen = 63%

Alternatively, if 37 people out of 100 are NOT freshmen, then 37% are not freshmen, This means that 100% – 37% = 63% ARE freshmen.

 

3. An online dating site claims that it background checks all of its members.

Solution

ALL members means everyone, so out of 100 people, 100 people are background checked. \dfrac{100}{100}=100\%

Note that this means 100% = 1.

 

Explore 2 – The meaning of percent

A percent is a part-to-whole relationship between two measures. For example, in a sale of 40% off the regular price, the part is the discount and the whole is the original price. Identify the measures of the part (the numerator) and the whole (the denominator) of the percents in the following expressions.

  1. Sales tax in Utah County is 7.25% and is added to the cost of many purchases.

Solution

The part is the tax and the whole is the cost of purchase before tax.

  Tax gets added to the purchase price.

  1. Josie left a 25% tip for the dinner.

Solution

The part is the tip and the whole is the cost of the dinner.

Tip gets added to the dinner price

  1. The number of students at a university decreased 3% this year from last year.

Solution

The part is the number of decreased students and the whole is the number of students in total.

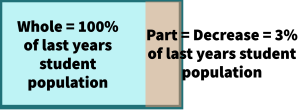A decrease is subtracted from the whole.

  1. Kioni got 95% on his math midterm.

Solution

The part is Kioni’s test score and the whole is the total possible score of the midterm.

 

Examples

  1. Write 45% as a simplified fraction.
  2. Write 130% as a simplified fraction.
  3. The U.S. unemployment rate was 3.5% in March 2023.[2]. Write 3.5% as a simplified fraction.
  4. On a survey of 100 people, only 26 claimed a favorable opinion of the news media in the United States. Write this ratio as a percent.
  5. 4 out of 10 dogs prefer Chow Down dog food. Write this ratio as a percent.

Identify the measures of the part and the whole of the percents in the expression. Show how the percent is formed from the part and the whole. Draw a diagram that shows the relationship between these two measures.

  1. Jan has a new job where he gets a base salary and 4% commission on sales.
  2. Alex invests an inheritance of $20,000 in an account that gains 5% interest.
  3. Your favorite jeans store is having a 50% off sale.

 

Show/Hide Answer

1.  45\%=\dfrac{45}{100}=\dfrac{9}{20}

2.  130\%=\dfrac{130}{100}=\dfrac{13}{10}

3.3.5\%=\dfrac{3.5}{100}=\dfrac{35}{1000}=\dfrac{7}{200}

4. \dfrac{26}{100}=26\%

5. \dfrac{4}{10}=\dfrac{40}{100}=40\%

6.

Whole = sales; part = commission          \dfrac{Commission}{All sales}=4\%

7.

  Whole = investment of $20,000; part = interest          \dfrac{Interest}{Investment}=5\%

8.

   Whole = regular price of jeans; part = discount          \dfrac{Discount}{Original price}=50\%

 

Reflect Icon

  • Why is a percent dimensionless?
Show/Hide Answer

A percent is just a fraction with a denominator of 100, and numbers by themselves have no dimension. A percent is not a measurement.

  • Explain why a percentage of a measurement is a measurement.
Show/Hide Answer

A percent is just a fraction with a denominator of 100, but a percentage of a measurement is a fraction of a measurement,  and a fraction if a measurement is still a measurement. To find a fraction of a measurement, we multiply the measurement by the fraction. The product is a measurement because the units are retained during multiplication. For example, the 50% of 100 cm = \dfrac{50}{100}\times100 cm=50 cm.

 

Practice Exercises

  1. A local charity states that 13 cents out of every dollar sent to them goes directly to their after-school program. What percentage of their donations have gone to their after-school program? 
  2. In New Mexico, 46 out of 100 top executive positions are held by females, the highest share of any state in the country. In Utah, only 24 out of 100 top executive positions are held by females.[3] Write the two ratios as percents.
  3. 20 out of 100 teens said they use YouTube “almost constantly”. Write this ratio as a percent.
  4. Write this 80% as a simplified fraction.
  5. The percentage of U.S. adults aged 18 and older who say they drink alcohol averaged 63% over the past two years, whereas 36% described themselves as “total abstainers.”[4] Out of 100 people, how many say they drink alcohol and how many are total abstainers?
  6. Your favorite clothes store is having an end-of-season 60% off sale on sweaters. Identify the part and the whole that makes up the percentage.

 

Show/Hide Answer
  1. 13%
  2. 46%; 24%
  3. 20%
  4. \dfrac{4}{5}
  5. 63 drink alcohol and 36 are total abstainers.
  6. Whole = original price; part = discount;  \dfrac{Discount}{Original\;Price}=60\%

 

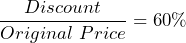
Explore Icon Conversions between Decimals and Percents

Since a percent is just a fraction with a denominator of 100, it can also be written as a decimal number. Converting between percents and decimals is relatively straightforward since both percents and decimals deal with hundredths. For example, 0.51 is 51 hundredths, and 51 hundredths as a fraction is \frac{51}{100}, which in turn is 51%. Similarly, we may convert a percent into a decimal by replacing the % sign with ÷ 100. For example, 38% is equal to \frac{38}{100}=38\div100=0.38.

 

Explore 3 – Conversions between decimals and percents

Convert the following decimal numbers to percentages and percentages to decimal numbers.

1. The ratio of males in a class was 0.49.

Solution

0.49=\dfrac{49}{100}=49\%

2. The interest rate on a saving account was 0.0125.

Solution

0.0125=\dfrac{1.25}{100}=1.25\%

3. The amount of snow this season was 1.20 times normal.

Solution

1.20=\dfrac{120}{100}=120\%

4. Hannah was given a wage increase of 0.003 times her current wage.

Solution

0.003=\dfrac{0.3}{100}=0.3\%

5. Use the pattern in your solutions to write a rule that tells us how to convert decimals to percentages.

Solution

Move the decimal place 2 place to the right and add a % sign. This is equivalent to multiplying the decimal number by 100%.

6. The stock market gained 3.5% today.

Solution

3.5\%=\dfrac{3.5}{100}=0.035

7. The birth control pill is 99% effective.

Solution

99\%=\dfrac{99}{100}=0.99

8. A 2023 Fox Sports headline claimed the Ravens were 200% committed to Lamar Jackson as quarterback.[5]

Solution

200\%=\dfrac{200}{100}=2

9. 0.125% Bupivacaine with epinephrine is often used as a lumbar epidural analgesia during labor.

Solution

0.125\%=\dfrac{0.125}{100}=0.00125

10. Use the pattern in your solutions to write a rule that tells us how to convert percentages to decimals.

Solution

Move the decimal point 2 places to the left and remove the % sign. This is equivalent to replacing the % sign with ÷ 100 and evaluating.

 

Explore 4 – Conversions between decimals and percentages

1. A shop has a sign that lists their t-shirts on sale for 40% off. Write 40% as a decimal.

Solution

We replace the % sign with ÷ 100:  40\%=\dfrac{40}{100}=0.4

2. The Sierra Nevada snowpack is about 200% of normal for the season up to March 10th 2023. Write 200% as decimal.

Solution

We replace the % sign with ÷ 100:  200\%=\dfrac{200}{100}=2

3. A batter’s batting average is calculated by dividing their total number of hits by the number of times they are at bat. If a batter’s batting average is 0.325, what percent of at-bats did the batter get a hit?

Solution

We want to introduce percent so we multiply the number by 100, and then divide the result by 100.   0.325=(0.325\times100)\div100=32.5\div100=\dfrac{32.5}{100}=32.5\%. This process, in summary, is to move the decimal point 2 places to the right and add the percent sign.

4. The probability of getting a head if flipping a fair coin is 0.5.

Solution

We want to introduce percent so we multiply the number by 100, and then divide the result by 100. 0.5=(0.5\times100)\div100=50\div100=\dfrac{50}{100}=50\%. This process, in summary, is to move the decimal point 2 places to the right and add the percent sign.

 

Conversions of Decimals and Percents

To convert from a percent to a decimal, replace  % with ÷ 100 and evaluate.

To convert from a decimal to a percent, multiply the decimal by 100%.

 

 

Reflect Icon

  • Why does 200% mean twice and 300% mean three times?
Show/Hide Answer

200% is equal to \dfrac{200}{100}, which means the part (i.e., 200) is twice as large as the whole (i.e., 100). In addition, 200% = 2, and 2 times anything is twice. Similarly, 300% is equal to \dfrac{300}{100}, which means the part (i.e., 300) is three times as large as the whole (i.e., 100). In addition, 300% = 3.

  • Why is it appropriate to multiply a decimal by 100% to get a percentage? Doesn’t multiplying by 100% change the value of the decimal?
Show/Hide Answer

Multiplying by 100% is equivalent to multiplying by 1, so the value of the decimal is not changed and the % sign is introduced to the number.

  • Explain how to turn a percentage into a decimal.
Show/Hide Answer

The percent sign, %, means each hundred, so we replace the % sign with ÷ 100, then evaluate.

 

 

Practice Exercises

Convert the following decimal numbers to percentages and percentages to decimal numbers.

  1. 95% of teens have access to a smartphone.
  2. 45% of girls say they are addicted to Tik-Tok [6]
  3. Personal income increased 0.3 percent in February 2023. [7]
  4. Apple will use 100% recycled cobalt batteries by 2025. [8]
  5. In 1984, Salt Lake City established the Percent for Art ordinance, allocating a percentage of eligible City project funds for commissioning artists for services and site-specific artwork to be integrated into new construction projects. As of 2021, that percentage is 0.015.
Show/Hide Answers
  1. 95% = 0.95
  2. 45% = 0.45
  3. 0.3% = 0.003
  4. 100% = 1
  5. 0.015 = 1.5%

 

 

Explore Icon Conversions between Fractions and Percentages

When the denominator of a fraction is 100, it is a straightforward process to directly convert the fraction to a percent using the numerator. For example, \dfrac{21}{100} = 21%. If the denominator is not 100, we have two options.

If our goal is to end up with a decimal percent, we may convert the fraction into a decimal first, then turn the decimal into a percent. For example, the fraction \dfrac{1}{5} is equal to 0.2 (1\div5=0.2). Then, we turn the decimal 0.2 to a percent. That is, 0.2=(0.2\times100)\div100=20\div100=\dfrac{20}{100}=20\%. If the fraction has repeating decimal places, for example, \dfrac{2}{3} = 0.6666.... Then, we may turn the decimal to a percent and then round the percent to a whole percent. That is, 0.6666... = (0.6666...\times100)\div100=66.66...\div100=\dfrac{66.66...}{100}=66.66...\%=67\%.

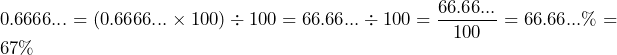If our goal is to have a fractional percent we multiply the fraction by 100% and simplify. For example, \dfrac{2}{3}=\dfrac{2}{3}\times100\%=\dfrac{200}{3}\%=66\frac{2}{3}\%.

Converting a decimal percent into a fraction uses the fact that % means divide by 100. We divide by 100, then we simplify the resulting fraction. For example, 60\%=\dfrac{60}{100} which simplifies to \dfrac{3}{5}. If a percentage has digits after the decimal point, we build the fraction by multiplying the numerator and denominator by a multiple of 10 to get a whole number, and then simplify the fraction. For example, 3.86\%=\dfrac{3.86}{100}=\dfrac{3.86\times100}{100\times100}=\dfrac{386}{10,000}=\dfrac{193}{5000}.

 

Explore 5 – Conversions between fractions and percentages

Convert the following fractions into percentages and percentages into fractions.

1. Collectors prize models of cars that are \dfrac{1}{8}th the size of the original car.

Solution

Way 1: To convert a fraction to a percent, we first convert the fraction to a decimal \dfrac{1}{8}=1\div8=0.125, and then convert the decimal to a percentage 0.125=(0.125\times100)\div100=12.5\div100=\dfrac{12.5}{100}=12.5\%.

Way 2: To convert a fraction to a percent, we multiply the fraction by 100%:  \dfrac{1}{8}=\dfrac{1}{8}\times100\%=\dfrac{100}{8}\%=\dfrac{25}{2}\%=12\frac{1}{2}\%. Alternatively, we divide the fraction to make an equivalent decimal, then multiply by 100%:  \dfrac{1}{8}=0.125=12.5\%.  Either way, we get the same solution: \dfrac{1}{8}=12\frac{1}{2}\%=12.5\%.

 

2. At 5 minutes to the hour, \dfrac{11}{12}th of the hour has passed.

Solution

Way 1: To convert a fraction to a percent, we first convert the fraction to a decimal \dfrac{11}{12}=11\div12=0.9166..., and then convert the decimal to a percentage 0.91666...=(0.9166...\times100)\div100=91.66...\div100=\dfrac{91.66...}{100}=92\%.

Way 2:To convert a fraction to a percent, we multiply the fraction by 100%:  \dfrac{11}{12}=\dfrac{11}{12}\times100\%=\dfrac{1100}{12}\%=\dfrac{275}{3}\%=91\frac{2}{3}\%. Alternatively, we divide the fraction to make an equivalent decimal, then multiply by 100%:  \dfrac{11}{12}=0.91\overline{6}=91.\overline{6}\%.  Either way, we get the same solution: \dfrac{11}{12}=91\frac{2}{3}\%=91.\overline{6}.

3. According to Statistica, 11/25 of U.S. students used marijuana in 2020.

Solution

Way 1: To convert a fraction to a percent, we first convert the fraction to a decimal \dfrac{11}{25}=11\div25=0.44, and then convert the decimal to a percentage 0.44=(0.44\times100)\div100=44\div100=\dfrac{44}{100}=44\%.

Way 2: To convert 11/25 to a percent, we multiply by 100%:  \dfrac{11}{25}=\dfrac{11}{25}\times100\%=44\%

 

4. After decades of decline in humanities divisions across college campuses, the University of California, Berkeley has reported a resurgence of students declaring majors in the Division of Arts and Humanities — an increase of 73 percent compared to ten years ago.[9]

Solution

To convert 73% to a fraction, we replace % by ÷ 100:  73\%=\dfrac{73}{100}

5. 80% of Gen Z (born between 1997 and 2012) believe they can only afford a home if it is priced below $200,000. Write 80% as a simplified fraction.

Solution

To convert a percent to a fraction, we replace % with ÷ 100 and evaluate:

80\%=\dfrac{80}{100} = \dfrac{4}{5}. 

6. Write 43.75% as a simplified fraction.

Solution

To convert a percent to a fraction, we replace % with ÷ 100 and evaluate:

43.75\%=\dfrac{43.75}{100}.

Since there should be no decimal places in the numerator, we may turn the decimal 43.75 to a whole number by expanding the fraction (multiplying the numerator and denominator by 100) and get

43.75\%=\dfrac{43.75\times100}{100\times100}=\dfrac{4375}{10000}.

Then, we may simplify the fraction and get \dfrac{4375}{10000}=\dfrac{7}{16}

 

 

Reflect Icon

  • What are the pros and cons of using a fraction and using a percentage in representing a relative size relationship (i.e., part to whole)?
Show/Hide Answer

Answers may vary. While it may be more intuitive for some people to see the size of the part with respect to the size of the whole in terms of “out of 100”, other people may like fractions where the denominators do not have to be 100. For example, the recipe ratio 2/5 (e.g., sugar to flour) may be more useful than 40% (e.g., the amount of sugar is 40% of the amount of flour).

 

Practice Exercises

  1. Ted spends 2/5 of his income on groceries. What percent of his income is spent on groceries?
  2. Mallory complains that 5 out of 7 days are spent working, and that is too much! What percent of days are spent working? Round the percentage to two decimal places.
  3. O’Neil makes 40% of his free throws. If he 5 free throws over the past two weeks, how many did he make?
  4. According to the Red Cross, less than 2% of the population have B negative blood.[10] Write the percentage as a simplified fraction.
  5. Americans think global warming is happening, outnumbering those who don’t by 5 to 1. [11]. Write the percent of Americans who do think global warming is happening.
  6. The probability of rolling two sixes with a pair of fair dice is 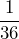\dfrac{1}{36}. Write this fraction as a percent.
Show/Hide Answers
  1. 40%
  2. 71.43%
  3. 2
  4. \dfrac{1}{50}
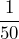
  5. 5:1 means 5 believe and 1 does not believe so, 5 out of 6 believe = 83.3%
  6. 2.78%

 

 

In this section, we will take what we have learned and apply the concepts to new situations.

Perspectives

  1. Nutrition Lab for M&Ms. Total fat = 6g; Saturated fat = 4g; Total carbs = 21g; total sugars = 20g The nutrition label to the right is for M&Ms. a) What percent of total fat is accounted for by saturated fat?  b) What percent of total carbohydrates is accounted for by total sugars?
  2. A beginning psychology course has exactly 100 students enrolled. Of those students, 40 have brown hair, 15 live off campus, and 78 work full time. a) What percentage of students have brown hair?  b) What percentage of students live off campus?  c) What percentage of students work full time?  d) According to the University 97% of students have a smartphone, how many students in this course would you expect NOT to have a smartphone?
  3. Ruby hit the ball 5 out of 6 times at-bat during her last softball game. What percent of her at-bats did she hit a ball? 
  4. The local soccer team won 65% of their games. Their season consisted of 20 games, how many did they win? 
  5. A diagnostic medical test was administered to 500,000 individuals and was positive 2,340 times. What percentage of the test results were positive?
  6. A doctor states that 2/5 of men over the age of 40 suffer from sleep apnea. What percentage of men over 40 have sleep apnea?
  7. Between 1501 and 1866, it is estimated that over 12.5 million people were forced onto ships in Africa, and transported to the Americas as slaves. Furthermore, it is estimated that only 10.7 million of these slaves disembarked on the other side of the Atlantic, meaning that roughly 1.8 million did not survive the journey.[12] What percent did not survive the journey?
  8. To the surprise of many, 60.1% of people who watch Cartoon Network are adults between 18 and 49 years old. Out of 1000 adults between 18 and 49, how many watch Cartoon Network?
Show/Hide Answers
  1. a) 66.67%    b) 95.24%
  2. a) 40%    b) 15%    c) 78%    d) 3
  3. 83.33%
  4. 13
  5. 0.468%
  6. 40%
  7. 14.4%
  8. 601

 

 

Skills IconIn this section, we will use what we have learned so far to practice skill problems.

 

Skill Exercises

Write the decimals and percentages and the percentages as decimals:

    1. 36%
    2. 7.5%
    3. 22.5%
    4. 350%
    5. 12.5%
    6. 0.65
    7. 0.78
    8. 9.4
    9. 1.345
    10. 0.0054

Write the fractions as percentages and the percentages as simplified fractions:

 

    1. \dfrac{4}{5}

 

    1. \dfrac{10}{5}

 

    1. \dfrac{8}{8}

     

    1. \dfrac{9}{10}
    1. \dfrac{54}{5}
    1. 1.25%
    1. \dfrac{9}{10}\%
    1. 0.45%
    1. \dfrac{4}{5}\%
    1. 222%

 

Show/Hide Answers
    1. 0.36
    2. 0.075
    3. 0.225
    4. 3.5
    5. 0.125
    6. 65%
    7. 78%
    8. 940%
    9. 134.5%
    10. 0.54%
    11. 80%
    12. 200%
    13. 100%
    14. 90%
    15. 1080%

     

    1. \dfrac{1}{80}
    1. \dfrac{9}{1000}
    1. \dfrac{9}{2000}
    1. \dfrac{1}{125}
    1. \dfrac{111}{50}

 

  1. https://www.redcross.org/donations/demystifying-the-donation.html ↵
  2. https://www.bls.gov/news.release/empsit.nr0.htm ↵
  3. https://www.usnews.com/news/best-states/articles/2023-03-06/states-with-the-highest-percentage-of-women-in-business-leadership-roles ↵
  4. https://news.gallup.com/poll/467507/percentage-americans-drink-alcohol.aspx ↵
  5. https://www.foxsports.com/stories/nfl/john-harbaugh-ravens-200-percent-committed-to-lamar-jackson ↵
  6. https://www.msnbc.com/morning-joe/watch/45-percent-of-girls-who-use-tiktok-say-they-feel-addicted-to-it-report-168410181667 ↵
  7. https://www.bea.gov/news/2023/personal-income-and-outlays-february-2023 ↵
  8. https://www.apple.com/newsroom/2023/04/apple-will-use-100-percent-recycled-cobalt-in-batteries-by-2025/ ↵
  9. https://artshumanities.berkeley.edu/news/increase-humanities-majors-uc-berkeley-opens-conversation-value-humanities-education ↵
  10. https://www.redcrossblood.org/donate-blood/blood-types/b-blood-type.html#:~:text=About%209%25%20of%20the%20population,positive%20and%20AB%20positive%20patients. ↵
  11. https://environment.yale.edu/news/article/by-5-to-1-ratio-americans-think-global-warming-is-happening ↵
  12. https://www.statista.com/statistics/1143207/slaves-brought-from-africa-to-americas-1501-1866/ ↵
definition

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

Numeracy Copyright © 2023 by Utah Valley University is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.