CHAPTER 3: RELATIVE MEASUREMENT

3-2: Unit Rates

What is a Unit Rate?

A unit rate is a rate with a denominator of 1 unit. Unit rates are very common in our everyday lives and help put things on a level playing field so comparisons can be made. Examples of unit rates are a speed of 50 miles per hour or $20.99/1 lb. of coffee. We usually say per hour or per pound instead of saying per 1 hour or per 1 pound. Either way the denominator is 1 unit. Unit rates are very important as they allow us to make comparisons with other unit rates. For example, when a product costs $5/2lb and $12/5lb, it is not obvious which choice is the cheaper offer. But by turning these into unit rates, we get $5/2 lb = $2.50/1 lb (or $2.50 per pound) and $12/5 lb = $2.40/ 1 lb (or $2.40 per pound), it is now obvious that the second option is the cheaper offer.

Explore Icon Unit Rates

To turn a rate into a unit rate, we need to make the denominator of the fraction equal to 1. We can do this by simply dividing the number in the denominator by itself, but, since a rate is a fraction, if we divide the denominator, we must also divide the numerator by the same number. Consequently, we are writing an equivalent rate fraction by simplifying the rate fraction (i.e., dividing both the numerator and denominator by the number in the denominator). For example, to convert the rate $5/2 lb to the unit rate $2.50/1 lb, we divide the numerator (5) and the denominator (2) by 2:

\begin{aligned}\dfrac{\$5}{2\;lb}&=\dfrac{\$5\div2}{2\;lb\div2}\\\\&=\dfrac{\$2.50}{1\;lb}\end{aligned}

 

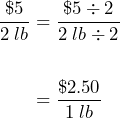
Explore 1 – Calculating unit rates

  1. Marcus likes to drive very fast. He makes it from Provo to Las Vegas (379 miles) in 3.7 hours. Calculate how fast he is going on average in miles per hour as a unit rate. Round the unit rate to the nearest whole mile per hour.

Solution

We start by writing the speed as a rate of mile/hours then turn the rate into a unit rate by dividing both the numerator and denominator by the number on the denominator:

\begin{aligned}\text{Average speed}&=\dfrac{379\;miles}{3.7\;hours}\\\\&=\dfrac{379\;miles\div3.7}{3.7\;hours\div3.7}\\\\&=\dfrac{102.4\;miles}{1\;hour}\end{aligned}.

Marcus’ average speed was about 102 miles per hour.

 

  1. A jar of peanut butter costs $2.19 for 15 ounces. What is the cost in dollars per ounce as a unit rate? Round the unit rate to the nearest cent.

Solution

To turn a rate into a unit rate we divide both the numerator and denominator by the number on the denominator:

\begin{aligned}\text{Cost per ounce}&=\dfrac{\$2.19}{15\;oz}\\\\&=\dfrac{\$2.19\div15}{15\;oz\div15}\\\\&=\dfrac{\$0.146}{1\;oz}\end{aligned}.

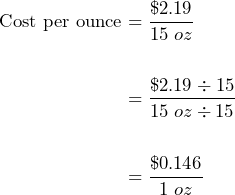This rounds to $0.15 per ounce or 15 cents per ounce.

 

  1. Usain Bolt of Jamaica currently holds the world record for running 100 meters in 9.58 seconds. Write his average speed in meters per second. Round the unit rate to the nearest hundredths place.

Solution

We start by writing the speed as a rate of mile/hours then turn the rate into a unit rate by dividing both the numerator and denominator by the number on the denominator:

\begin{aligned}\text{Average speed}&=\dfrac{100\;meters}{9.58\;seconds}\\\\&=\dfrac{100\;m\div9.58}{9.58\;sec\div9.58}\\\\&\approx\dfrac{10.438\;m}{1\;sec}\end{aligned}.

Usain Bolt’s average speed is 10.44 meters per second.

 

Explore 2 – Interpretations of unit rates

For a rate, the measure (also called the independent measure) that measures or determines the other measure is placed in the denominator of the rate. The measure in the numerator of the rate is called the dependent measure. However, there are situations where it can make sense to have either one of the two measures of a rate placed in the denominator. After placing different measures in the denominator, the meanings are also different.

 

A Honda Accord can travel 360 miles using 16 gallons of gasoline.

  1. Write the miles travelled per gallon as a unit rate.

Solution

We start by writing a rate with miles traveled on the numerator and gallons of gas on the denominator, then we simplify:

\dfrac{360\;miles}{16\;gallons}=\dfrac{360\;miles\div16}{16\;gallons\div16}=\dfrac{22.5\;miles}{1\;gallon} = 22.5 miles per gallon. 

 

  1. Write the gallons per mile as a unit rate. Round your rate to the nearest thousandths place.

Solution

We start by writing a rate with gallons of gas on the numerator and miles travelled on the denominator, then we simplify:

\dfrac{16\;gallons}{360\;miles}=\dfrac{16\;gallons\div360}{360\;miles\div360}\approx\dfrac{0.0444\;gallon}{1\;mile} = 0.044 gallons per mile. 

 

  1. What is the difference between these two rates?

Solution

The dependent measure (on the numerator) and the independent measure (on the denominator) are different. One rate is the reciprocal of the other rate i.e. the numerator and denominators have changed places. The first rate measures average miles traveled per gallon. The second rate measures the number of gallons of gas needed to travel one mile.

 

Examples

  1. A Prius can travel 944 miles using 8 gallons of gasoline. a) Write the miles per gallon as a unit rate. b) Write the gallons per mile as a unit rate. c) What is the difference between these two rates?
  2. A copy machine makes 40 copies in 25 seconds. a) Write the copies per second as a unit rate.  b) Write the time per copy as a unit rate.  c) Explain the difference between these two rates.

 

Show/Hide Answers
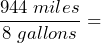  1. a) \dfrac{944\;miles}{8\;gallons}= 118 miles per gallon.    b) 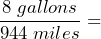\dfrac{8\;gallons}{944\;miles}= 0.008 gallons per mile.     c) The first rate measures the average number of miles that can be traveled on a gallon of gas. The second rate rate measures the number of gallons of gas required to travel 1 mile.
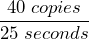  2. a) \dfrac{40\;copies}{25\;seconds} = 1.6 copies per second.  b) 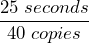\dfrac{25\;seconds}{40\;copies} = 0.625 seconds per copy. c) The first unit rate tells us that the machine makes 1.6 copies per second. The second unit rate tells us that it takes 0.625 seconds to make a single copy.

 

 

Reflect Icon

  • What does a unit rate tell us?
Show/Hide Answer

A unit rate tells us the relative relationship between two measures. In particular, a measure is determined by another measure per 1 unit. For example, the wage $10 per hour tells us the measure $10 is determined by the measure 1 hour .

  • Is it true that any rate can be converted into a unit rate? Explain your reasoning.
Show/Hide Answer

Mathematically, any rate can be converted into a unit rate (by dividing the numerator and the denominator of a rate by the number in the denominator). However, there may be some real life situations that force the rates to go by a denominator that cannot be one. For example, there may be a sign saying $10 per 5 items for some product that is on sale in a supermarket, and the deal is only available if you buy 5 items. In other words, you may need to pay the regular price (e.g., $2.99 per item) if you buy 1 or 2 or 3 or 4 items.

 

 

Practice Exercises

  1. Ron ate 25 hot dogs in 4 minutes. Write the unit rate.
  2. John ran a marathon (26 miles) in 5 hours. Write the unit rate.
  3. Ethan and Ellen work at a local grocery store stocking shelves. Ethan takes 20 minutes to stock 3 shelves, while Ellen takes 30 minutes to stock 6 shelves. Who is the faster worker?
  4. Jane and Jerry are running laps. Jane runs 5 laps in 20 minutes, while Jerry runs 8 laps in 35 minutes. Who is the faster runner?
  5. Hugh paid $559.80 for 15 tons of coal that he will use to heat his home. Determine the price of coal per ton.
Show/Hide Answer
  1. 6.25 hot dogs per minute
  2. 5.2 miles per hour
  3. Ellen
  4. Jane
  5. $37.32 per ton

 

Explore Icon Comparing Rates

Explore 3 – Interpretations of unit rates in comparison

A 12-ounce bottle of ketchup is on sale for $0.99. A larger 20-ounce bottle of the same ketchup has a regular price of $2.49. 

  1. Write a unit rate of dollars per ounce for each of the two products. Round the rates to the nearest hundredths place. 

Solution

To write the rates of dollar per ounce, we need dollars on the numerator and ounces on the denominator. Then we divide both the numerator and denominator of the rate by the number on the denominator to determine the unit rate.

The ketchup that is on sale has a unit rate of:

\begin{aligned}\dfrac{\$0.99}{12\;oz}&=\dfrac{\$0.99\div12}{12\;oz\div12}\\\\&=\$0.08\text{ per ounce}\end{aligned}

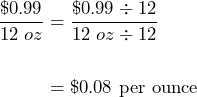
The larger bottle of ketchup has a unit rate of :

\begin{aligned}\dfrac{\$2.49}{20\;oz}&=\dfrac{\$2.49\div20}{20\;oz\div20}\\\\&=\$0.12\text{ per ounce}\end{aligned}

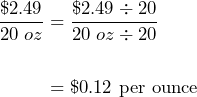
  1. Write a unit rate of ounces per dollar for each of the two products.

Solution

To write the rates of ounce per dollar, we need ounces on the numerator and dollars on the denominator. Then we divide both the numerator and denominator of the rate by the number on the denominator to determine the unit rate.

The bottle on sale unit rate of:

\begin{aligned}\dfrac{12\;oz}{\$0.99}&=\dfrac{12\div 0.99}{\$0.99\div 0.99}\\\\&=\dfrac{12.12}{\$1}\\\\&=12.12\text{ ounces per dollar}\end{aligned}

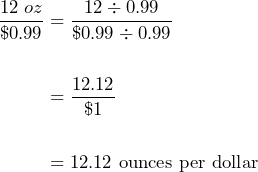
The larger bottle has a unit rate of:

\begin{aligned}\dfrac{20\;oz}{\$2.49}&=\dfrac{20\;oz\div2.49}{\$2.49\div2.49}\\\\&=8.03\text{ ounces per dollar}\end{aligned}

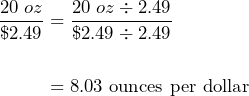
Based on the unit rate dollars per ounce, which bottle is the better deal?

Solution

The bottle that is on sale is the better deal because it is cheaper at $0.08 per ounces than the larger bottle at $0.12 per ounce.

  1. Based on the unit rate ounces per dollar, which bottle is the better deal?

Solution

The bottle that is on sale is the better deal because we get more ketchup per dollar: 12.12 ounces versus 8.03 ounces.

  1. According to your answers for questions 3 and 4, is it true that the smaller unit rate is always the better deal? Explain your reasoning

Solution

No. It depends on the context of the rates. For the two rates of dollars per ounce, the smaller rate is cheaper because it costs less money for buying one ounce of ketchup. However, for the two rates of ounces per dollar, the smaller rate is more expensive because you get less ketchup for one dollar.

 

Explore 4 – Comparing rates

In Arapahoe County, Colorado, before marijuana possession became legal in 2012, there were thousands of marijuana possession arrests. In 2010, there were 2263 arrests made of white individuals and 8882 arrests of Black individuals. In 2014, there were 889 arrests of white individuals and 2,301 arrests of Black individuals. [1]

  1. What is the unit rate of possession arrests per month for each race in 2010?

Solution

For white individuals, the rate is:

\begin{aligned}\dfrac{2263\text{ arrests}}{1\text { year}}&=\dfrac{2263\text{ arrests}}{12\text{ months}}\\\\&=\dfrac{2263\text{ arrests}\div12}{12\text{ months}\div{12}}\\\\&\approx 188.6\text{ arrests per month}\end{aligned}

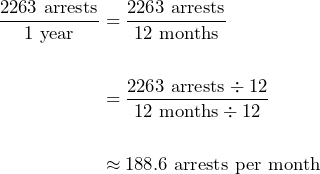
For Black individuals, the rate is:

\begin{aligned}\dfrac{8882\text{ arrests}}{1\text { year}}&=\dfrac{8882\text{ arrests}}{12\text{ months}}\\\\&=\dfrac{8882\text{ arrests}\div12}{12\text{ months}\div{12}}\\\\&\approx 740.2\text{ arrests per month}\end{aligned}

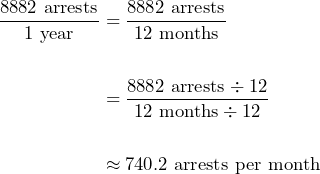
  1. In 2010, how many times as many Black individuals were arrested for possession per month compared to white individuals?

Solution

Dividing the rates:

\dfrac{740.2\text{ arrests per month}}{188.6\text{ arrests per month}}\approx 4

Black individuals were arrested for marijuana possession at about 4 times the rate of white individuals.

  1. What is the unit rate of possession arrests per month for each race in 2014?

Solution

For white individuals, the rate is:

\begin{aligned}\dfrac{889\text{ arrests}}{1\text { year}}&=\dfrac{889\text{ arrests}}{12\text{ months}}\\\\&=\dfrac{889\text{ arrests}\div12}{12\text{ months}\div{12}}\\\\&\approx 74.1\text{ arrests per month}\end{aligned}

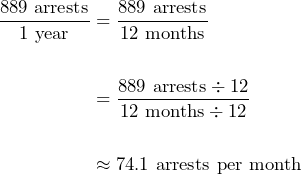
For Black individuals, the rate is:

\begin{aligned}\dfrac{2301\text{ arrests}}{1\text { year}}&=\dfrac{2301\text{ arrests}}{12\text{ months}}\\\\&=\dfrac{2301\text{ arrests}\div12}{12\text{ months}\div{12}}\\\\&= 191.75\text{ arrests per month}\end{aligned}

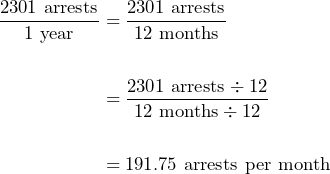
  1. In 2014, how many times as many Black individuals were arrested for possession per month compared to white individuals?

Solution

Dividing the rates:

\dfrac{191.75\text{ arrests per month}}{74.1\text{ arrests per month}}\approx 3

Black individuals were arrested for marijuana possession at about 3 times the rate of white individuals.

  1. Did the gap between Black and white individuals in possession arrests reduce from 2010 to 2014?

Solution

Yes, but there is still a considerable difference.

 

 

Explore 5 – Comparing rates

According to Billboard, Jay-z is the greatest rapper of all time followed by Kendrick Lamar. Jay-z’s best album is Hard Knock Life Vol. 2 and Kendrick Lamar’s is D*mn. Jay-z sold 3,500,000 copies in 10 weeks. Kendrick Lamar sold 5,295,000 copies in 15 weeks. [2]

  1. What is the unit rate in albums sold per week for Jay-z?

Solution

3,500,000 copies in 10 weeks = \dfrac{3,500,000\text{ copies}}{10\text {weeks}}=\dfrac{3,500,000\text{copies}\div{10}}{10\text{ weeks}\div10}=350,000\text{ per week}

  1. What is the unit rate in albums sold per week for Kendrick Lamar?

Solution

5,295,000 copies in 15 weeks = \dfrac{5,295,000\text{ copies}}{15\text {weeks}}=\dfrac{5,295,000\text{copies}\div{15}}{15\text{ weeks}\div15}=353,000\text{ per week}

  1. Based on the unit rates, which rapper’s album sales indicate higher average weekly popularity? Provide a rationale for your choice.

Solution

Kendrick Lamar sold an average of 3,000 more albums per month than Jay-z sold, so Kendrick Lamar’s album sales indicate higher average weekly popularity.

 

Reflect Icon

  • Why is it important to use unit rates when making comparisons?
Show/Hide Answer

It is easier to compare two rates when both rates have the same denominator of 1, as in unit rates. We only need to compare the numerators with unit rates.

  • Is it necessary to convert all rates into unit rates when comparing the rates?
Show/Hide Answer

No, we do not have to as long as we are able to compare the rates correctly. It is much easier to compare rates when they have the same denominator.  For example, we know $4 per 5 items is cheaper than $3 per 5 items. It is not necessary to convert them into unit rates. Sometimes, you do not even need to convert rates into the same denominator. For example, you know 1 miles per two hour is slower than 5 miles per 6 hours because 1/2 is smaller than 5/6. However, it is easiest to compare unit rates.

 

Practice Exercises

  1. A 12-pack of 12 fluid ounce cans of Coke costs $7.49. A 6-pack of 16.9 fluid ounce bottles of Coke costs $4.99. Calculate the rates of cost per fluid ounce. Which purchase is the better deal?
  2. You have just taken a new job as a salesperson and are offered two options for being paid: Option A is a salary of $4500 per month. Option B is a salary of $40,000 per year + $1000 per car sold. You believe you can easily sell 2 cars per month. Which option should you choose?
  3. Mark is shopping for dog food to donate the an animal sanctuary. Doggie Delights costs $46 for a 20 pound bag and Choice Chow costs $55 for a 25 pound bag. Determine the cheaper deal. Other than price per ounce, what else should be taken into consideration before purchasing?
  4. 100% Kona coffee beans cost $39 for 10 oz or $297 for 5 lb. Write the unit rates of cost per ounce and determine the better buy. Other than price per ounce, what else should be taken into consideration before purchasing?

 

Show/Hide Answer
  1. Cans: 5.2 cents per fl. oz.    Bottles: 4.9 cents per fl. oz.    Bottles are the cheaper deal.
  2. Option A: $4500 per month; Option B: 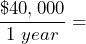\dfrac{\$40,000}{1\;year}= $3333.33 per month. 2 cars sold per month = 2·$1000 = $2000. So, total monthly wage is $5333.33.  Option B is the better option.
  3. Doggie Delights unit rate = $2.30 per pound. Choice Chow unit rate = $2.20 per pound. Choice Chow is the cheaper deal.  What is the better dog food as far as ingredients and quality are concerned?
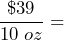  4. \dfrac{\$39}{10\;oz}= $3.90 per ounce.  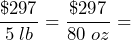\dfrac{\$297}{5\;lb}=\dfrac{\$297}{80\;oz}= $3.7125 per ounce.  The 5lb bag is the better deal.  What quantity of beans can you use before the beans go stale.

 

 

In this section, we will take what we have learned and apply the concepts to new situations.

Perspectives

  1. You receive a job offer with a salary of $35,000 per year. Assuming a 40-hour workweek, and 50 workweeks per year, what is your salary as a unit rate in dollars per hour?
  2. The code set in the American with Disabilities Act allows at most a vertical rise of 1 inch to every horizontal run of 1 foot when constructing wheelchair ramps. UVU engineers measure the library’s ramp and find that it has a rise of 14 inches and a run of 23 feet. Calculate the unit rate of rise to run for the library and determine if the library’s wheelchair ramp complies with the American with Disabilities Act.
  3. Your boss is determined to save money and has decided to fire the salesperson who is costing them the most money. Salesperson A earns an annual salary of $55,000 per year and sold 8,000 units last year; Salesperson B earns an annual salary of $48,000 and sold 6000 units last year; Salesperson C earns an annual salary of $40,000 and sold 3500 units last year. Calculate the unit rate of dollars per unit for each salesperson, then decide who should be let go.
  4. There are two apartments for rent that you are considering. The first is a 1-bedroom and has 800 square feet. The rent is $1250 per month. The second is a 1-bedroom and has 950 square feet. The rent is $1500 per month.  a) What is the unit rate for the first apartment in dollars per square foot?  b) What is the unit rate for the second apartment in dollars per square foot?  c) Which is the better buy based upon prices per square foot?  d) What other factors might you consider when looking for an apartment?
  5. You intend to stock up on toilet paper, just in case[3]. You have $100 to spend. Because you are stocking up, you would really like to buy the most inexpensive toilet paper you can find. At the store you see three different options:

Option A: 24 Two-ply Mega Rolls for $29.99, according to the package a mega roll contains 276 sheets.

Option B: 24 Two-ply Double Rolls for $19.99, according to the package a double roll contains 110 sheets.

Option C: 4 One-ply Regular Rolls for $2.99, according to the package a regular roll contains 70 sheets.

a) Calculate the unit rate of the number of sheets per dollar for each option above.

b) Calculate the unit rate of price per sheet for each option above. 

c) In your opinion, is finding the price per sheet more or less informative than the number of sheets per dollar?  Explain your reasoning?

d) Which option would you choose to buy? Why would you choose this option? 

e) What is the maximum number of sheets you can buy for $100? 

f) What other considerations should be made when making this purchase? 

  1. Farah manages a grocery store. She has determined that approximately 75 shoppers check out every hour. If it takes on average 7 minutes for each shopper to check out, how many checkers should Farah have on duty to avoid check-out lines?
  2. In 2021, Brown University researchers found that students closer to graduating experienced increases in anxiety, feelings of loneliness, and depression. The following data regarding the final weeks before graduation:

During the 4 weeks before graduation: 320 students reported increased anxiety.
During the 5 weeks before graduation: 430 students reported feelings of loneliness.
During the 6 weeks before graduation: 510 students reported feeling depressed.

During those final weeks:

a) What is the unit rate of anxiety reports per week?

b) What is the unit rate of feelings of loneliness per week?

c) What is the unit rate of depression reports per week?

If you are concerned about your mental health, seek support through UVU’s student health services.

Show/Hide Answer
    1. $20 per hour
    2. 0.61 inches per foot. Yes, it complies with the American with Disabilities Act.
    3. A: $6.875 per unit sold.  B: $8 per unit sold. C: $11.43 per unit sold. Salesman C should be let go.
    4. a) $1.56 per square foot.   b) $1.58 per square foot    c) The smaller apartment is the cheaper option per square foot.    d) location; contract; appearance; etc.
    5. a) A: 221 sheets per dollar. B: 132 sheets per dollar. C: 94 sheets per dollar.  b) A: $0.0045 per sheet.  B: $0.0076 per sheet.  C: $0.0106 per sheet.  c) Answers vary.  d) Answers vary.  e) 22, 100 sheets of option A.  f) Answers vary.
    6. Total time for 75 shoppers to check out = 525 minutes.  Number of checkers = 9.
    7. a) 80 students per week     b) 86 students per week    c) 85 students per week

 

Skills IconIn this section, we will use what we have learned so far to practice skill problems.

Skill Exercises

Write each rate as a unit rate:

    1. $4 for 5 oz.
    2. $26 per 2 lb.
    3. 340 miles in 6 hours.
    4. 220 minutes per 4 clients.
    5. 3 meters for $12.
    6. $4.99 for 14 ounces of dried sage.  
    7. Yolanda drove 340 miles in 5.5 hours.
    8. Sam paid $34.98 for 8 lattes.
    9. The floor had to withstand a pressure of 2560 lb per 250 ft2.
    10. The force of gravity was 166.6m per 17 sec2.

     

    1. \dfrac{\$26.78}{4.5 lb}

     

    1. \dfrac{575km}{5.4\;hours}

     

Write each rate as a unit rate:

    1. $4.50 per 1.5 lb.
    1. $9.99 for 2kg.
    2. 455 miles in 7.5 hours.

 

    1. \dfrac{300km}{2.4\;hours}

     

    1. \dfrac{\$1.2\;million}{12.5\;acres}

     

    1. \dfrac{760\; people}{2.5\; hours}

     

    1. \dfrac{16.2\;liters}{\$21.40}

     

    1. \dfrac{6525\;people}{348\;minutes}

     

 

Show/Hide Answer
    1. $0.80 per ounce
    2. $13 per pound
    3. 56.7 mph
    4. 55 minutes per client
    5. 0.25m per dollar
    6. $0.356 per oz.
    7. 61.8 mph
    8. $4.3725 per latte
    9. 10.24 pounds per square foot
    10. 9.8 meters per square second
    11. $5.95 per pound
    12. 106.48km per hour
    13. $3 per pound
    14. $4.995 per kilogram
    15. 60.67 miles per hour
    16. 125km per hour
    17. $96,000 per acre
    18. 304 people per hour
    19. 1.306 liters per dollar
    20. 18.75 people per minute

 

  1. https://www.aclu.org/report/tale-two-countries-racially-targeted-arrests-era-marijuana-reform ↵
  2. https://www.billboard.com/ ↵
  3. Adapted from https://www.bogleheads.org/forum/viewtopic.php?t=266360 ↵
definition

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

Numeracy Copyright © 2023 by Utah Valley University is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.