CHAPTER 3: RELATIVE MEASUREMENT
3-1: Ratios and Rates
Absolute and Relative Measures
An absolute measurement uses a measuring tool (e.g., a ruler, a scale) to measure an object, which we studied in chapter 2. A relative measurement uses a measurement to measure another measurement. For example, a cake recipe may require 3 cups of sugar for every 5 cups of flour. The measure of sugar (e.g., 3 cups) is determined by the measure of flour (e.g., 5 cups). As another example, if fruit is sold for $2.99 per pound, the measure of price (e.g., $2.99) is determined by the measure of weight (e.g., 1 lb).
 Ratios
Ratios
A ratio is a type of relative measure. A ratio is defined as a tool used to compare the size of two or quantities in relation to each other. A ratio can be written in words (3 to 2), using a colon (3:2), or as a fraction ![]() only if two quantities are compared. The first of the two quantities forming a ratio is called the antecedent and the second is called the consequent of the ratio. Together they are called the terms of the ratio. The antecedent and the consequent have the same unit of measurement. This means that the units of measurement simplify to 1 and the ratio is dimensionless.
only if two quantities are compared. The first of the two quantities forming a ratio is called the antecedent and the second is called the consequent of the ratio. Together they are called the terms of the ratio. The antecedent and the consequent have the same unit of measurement. This means that the units of measurement simplify to 1 and the ratio is dimensionless.
As a simplified fraction, the numerator (the antecedent) and the denominator (the consequent) cannot be interchanged unless there is a change in the statements. For example, a ratio of ![]() is not equal to a ratio of
is not equal to a ratio of ![]() . But if the ratio of
. But if the ratio of ![]() represented the ratio of sugar to flour in a recipe, then the ratio
represented the ratio of sugar to flour in a recipe, then the ratio ![]() would represent the measure of flour to sugar. The measures are interchanged only when the ingredients are reversed.
would represent the measure of flour to sugar. The measures are interchanged only when the ingredients are reversed.
A ratio is expressed as the numerator to the denominator. For example, a map scale may have a ratio 1 to 10,000 or ![]() . Since the units are the same, it could be 1 cm on the map to 10,000 cm in reality or 1 inch on the map to 10,000 inches in reality. In other words, since the ratio is fixed, any units may be assigned that make sense contextually to the ratio.
. Since the units are the same, it could be 1 cm on the map to 10,000 cm in reality or 1 inch on the map to 10,000 inches in reality. In other words, since the ratio is fixed, any units may be assigned that make sense contextually to the ratio.
Explore 1 – A ratio is a simplified fraction
- What units are best suited to a U.S. map that has a ratio of 1:50,000?
Solution
1 inch on the map represents 50,000 inches in reality.
- Lucas determines that the best lemonade is made with 8 cups of water, 1 cup of sugar and 1 cup of lemon juice. Find the ratios of water to sugar and sugar to lemon juice.
Solution
The ratio of water to sugar is 8 cups to 1 cup or ![]() . The ratio of sugar to lemon juice is 1 cup to 1 cup or
. The ratio of sugar to lemon juice is 1 cup to 1 cup or ![]() .
.
- At the Utah Dental Association conference, Colgate polled 200 dentists. They found that 160 of the polled dentists said they recommended Colgate to their patients. Write a ratio of recommending dentists to total dentists polled and interpret the result.
Solution
The ratio is ![]() . This means 4 out of 5 dentists recommend Colgate to their patients.
. This means 4 out of 5 dentists recommend Colgate to their patients.
- A recipe for Scottish shortbread requires 300 grams of plain flour, 100 grams of sugar and 200 grams of butter.

- a) What is the ratio of butter to sugar?
- b) What is the ratio of sugar to flour?
- c) What is the ratio of butter and sugar combined to flour?
- d) What is the ratio of butter and flour combined to the complete recipe?
Solution
- a) The ratio of butter to sugar is
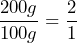 .
. - b) The ratio of sugar to flour is
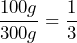 .
. - c) The ratio of butter and sugar combined to flour is
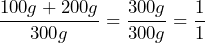 .
. - d) The ratio of butter and flour combined to the complete recipe is
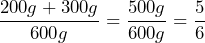 .
.
Explore 2 – A ratio is a measurement
ROI (return on investment) is a measure of the profitability of an investment. It is a ratio of the net income to the cost of investment. For example, if you made an investment of $10,000 last year and you receive $12,000 in revenue this year, your net income is ![]() . Your ROI ratio is
. Your ROI ratio is ![]() .
.
The Harlem Renaissance Cultural Center invested $80,000 in the restoration of a significant African American historical site. Following the restoration, the center generates an additional annual revenue of $15,000 through cultural tourism.
- Calculate the ROI for the cultural preservation investment of the Harlem Renaissance Cultural Center.
Solution
The net income is ![]() . The ROI ratio is
. The ROI ratio is ![]() .
.
- Is the ROI positive or negative? What does that tell us?
Solution
The ROI ratio is negative which indicates a loss, which could be considered a poor investment. The ratio tells us that for every $16 invested, they will lose $13.
-
Is it worth it to restore cultural sites?
Solution
Yes. Although the ROI ratio is negative for the first year, the $80,000 investment was a one time investment. For future years the investment is zero, and assuming a similar generation of $15,000 through cultural tourism every year, the net income for 10 years is ![]() and the ROI ratio is
and the ROI ratio is ![]() . As well as the financial aspect there is the cultural aspect and promotion of cultural heritage, which is priceless.
. As well as the financial aspect there is the cultural aspect and promotion of cultural heritage, which is priceless.
Explore 3 – A ratio is a measurement
The Waist-to-Hip ratio is used to measure the distribution of body fat and assess the risk of certain health conditions such as heart disease.
Here’s how the Waist-to-Hip ratio is calculated:
- Measure the waist at the smallest point – usually at the naval or just above it
- Measure the hips at the widest, largest part
- Find the ratio of the waist measurement to the hip measurement
- Convert the ratio to a decimal number. It is considered healthy for men if the ratio is 0.99 or lower. It is healthy for women if the ratio is 0.90 or lower.
What is the Waist-to-Hip ratio for Nadia if her waist is 36″ and her hip is 40″?
Solution
Nadia’s Waist-to-Hip ratio is ![]() . Therefore, Nadia’s ratio is healthy.
. Therefore, Nadia’s ratio is healthy.
Examples
- What units are best suited to an architectural plan of a house marked 1:10?
- Write the ratio of 30cm to 40cm.
- Write the ratio of 8 fl. oz. to 1 pint.
- Write the ratio of 400cm to 2km.
- Red, the Golden Retriever, had a litter of 8 puppies; 2 were male and 6 were female. Write the ratio of females to males.
- A packet of M&Ms had 7 yellows, 8 browns, 6 purples, 6 blues, and 9 reds. Write the ratio of reds to total M&Ms.
- If you draw all hearts from a deck of 52 cards, what is the ratio of the remaining cards to the whole deck?
Show/Hide Answer
- Depending on whether US Customary or SI units are used, 1:10 tells us 1 inch on paper represents 10 inches in reality, or (most commonly) 1 cm on paper represents 10 cm in reality.
- Ratio
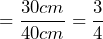
- Ratio
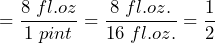
- Ratio
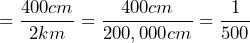
- Ratio
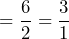
- Ratio
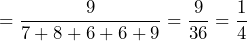
- There are 13 cards that are hearts, which means if you draw all hearts there are (52 – 13) = 39 cards left. Therefore, the ratio is
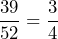 .
.

- Is it necessary to simplify a ratio?
Show/Hide Answer
Although it is not necessary, it is a common mathematical practice to simplify a fraction. A simplified fraction is usually easier for communication and understanding of mathematics. Since a ratio is expressed as a fraction, it is common to simplify a ratio.
- Does it matter which measure goes to the denominator/numerator of a ratio?
Show/Hide Answer
Yes. When asked for a ratio of this to that, this always goes on the numerator as the antecedent and that always goes on the denominator as the consequent: ![]()
- Why are ratios dimensionless i.e. they have no units of measurement?
Show/Hide Answer
A ratio has the same units of measurement on the numerator and denominator of the fraction. Consequently, the units cancel out to 1. This means that ratios are just fractions and numbers (like fractions) have no dimension.
Practice Exercises – Ratios
- What units are best suited to a drawing of a computer chip marked 200:1?
- A recipe calls for 6 oz of butter and 4 oz of sugar. What is the ratio of butter to sugar?
- A roof has a pitch such that for every 12 inches of horizontal distance, the roof rises 4 inches. Write the ratio of roof rise to horizontal distance.
- At a recent animated movie screening there were 3 times as many children as adults. Write the ratio of children to adults.
- In a standard deck of 52 playing cards, half are red and the other half are black. a) Write the ratio of red cards to black cards. b) Write the ratio of black cards to all cards.
Show/Hide Answer
- Computer chips are very small and the circuitry even smaller, so the drawing will be much larger than the chip. 200:1 could mean 200mm on paper represents 1mm on the chip.

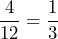

- a)
 b)
b) 
 Human Ratios
Human Ratios
On average, humans have about 7 inches of height for every 1 inch of foot length. Measure your height in inches, and your foot length in inches and create a ratio of height to foot length. Is your height to foot length approximately 7 to 1? Interpret your results.
 Rates
Rates
A rate is another type of relative measurement. A rate is a comparison of two measures with different units of measurement and can be written either as a simplified fraction or expressed using the word per between the measures. For example, the speed of a car may be 60 miles per hour. The equivalent fraction is ![]() . Notice that the measurement units are different, and therefore do not cancel. With a rate, the numerator is dependent upon the denominator. For example, if the time traveled changed to 2 hours, the distance traveled by the car would change to 120 miles, and the speed of the car would be
. Notice that the measurement units are different, and therefore do not cancel. With a rate, the numerator is dependent upon the denominator. For example, if the time traveled changed to 2 hours, the distance traveled by the car would change to 120 miles, and the speed of the car would be ![]() . This fraction, of course, simplifies to
. This fraction, of course, simplifies to ![]() . This is the exact opposite of ratios!
. This is the exact opposite of ratios!
Explore 4 – The difference between rates and ratios
Determine if each of the following measures is a rate or a ratio.
- A wage of $12 per hour.
Solution
Rate: the units are different ($ and hour) and the word per is used.
- The UVU student-to-faculty measure in 2023 is 22:1.
Solution
Ratio: the units are the same (people).
- The price of bananas is $0.69 per pound.
Solution
Rate: the units are different ($ and lb) and the word per is used.
- The relation between the height and the base of a triangle is
 .
.
Solution
Ratio: there are no measurement units
- The snow accumulation last tonight was 2 inches per hour.
Solution
Rate: the units are different (inches and hour) and the word per is used.
Explore 5 – A rate is a measure
Determining calorie density can help an individual determine the types of food to include in their diet, depending on their personal goals. Calorie density is calculated by using a rate to compare the number of calories in the food to the weight of the food.
- Calculate the calorie density of broccoli which has 51 calories for 153 grams.
Solution
Calorie density = calories to weight = ![]() .
.
- Calculate the calorie density of cheddar cheese which has 130 calories for 26 grams.
Solution
Calorie density = calories to weight = ![]() .
.
Explore 6 – A rate is a measure
Ben makes $21 dollars per hour working in the call center for a hotel. He answers on average 35 calls per hour. Calculate the rate of dollars per call and interpret the result.
Solution
We can use dimensional analysis to convert from ![]() to
to ![]() .
.
![]() .
.
This means that on average Ben makes $3 for every 5 calls he answers.
 Is a rate also a ratio?
Is a rate also a ratio?
Show/Hide Answer
The definition of a rate is the same as the definition of a ratio except for the part that the units of the two measures of a rate are different. Therefore, a rate is not a ratio.
Practice Exercises – Rates
- At a fundraiser, the catering company provides 350 potatoes and 820 pads of butter. What is the rate of pads of butter to potatoes? Simplify the rate to lowest terms.
- A family-size box of cereal contains 18 oz and sells for $4.99. Determine the rate of price per weight.
- Coca-Cola has 65 grams of sugar in a bottle containing 1.25 pints. Write the rate of sugar to the amount of Coca-Cola.
- It costs $56.80 for 8 burgers. Write this as a rate of cost per burger and simplify.
Show/Hide Answer
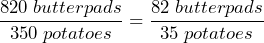
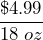
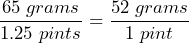
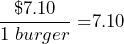 per burger
per burger
 In this section, we will take what we have learned and apply the concepts to new situations.
In this section, we will take what we have learned and apply the concepts to new situations.
Perspectives
- Using ratios, determine which rectangle is the closest to being a square. A rectangle that measures 22 inches by 25 inches or a rectangle that measures 18 inches by 21 inches. Explain your reasoning.
- You get 56 bushels of apples from 8 apple trees. Create a rate of bushels to trees and simplify. Interpret the results.
- A 16 inch pizza costs $20. Calculate the area of the pizza, then determine the cost per square inch of the pizza.
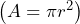
- A 12-pack of 12 fluid ounce cans of Coke costs $7.49. Write the rate of cost per fluid ounce.
- On April 6, 2023, the rate of exchange between U.S. dollars and Euros was $1 : €0.92. Explain what this ratio means.
- An architectural drawing has a scale of 1:200. If a beam measures 2 inches on the drawing, what will it measure in reality?
Show/Hide Answer
- A square has a side ratio of 1:1 , so the rectangle with a side ratio closest to 1/1 will be closest to being a square.
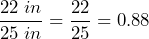 .
. 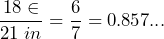 . SInce 0.88 is closer to 1 than 0.857, the rectangle that measures 22 inches by 25 inches is closer to being square.
. SInce 0.88 is closer to 1 than 0.857, the rectangle that measures 22 inches by 25 inches is closer to being square. 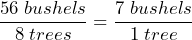 = 7 bushels per tree. This means that on average you will get 7 bushels of apples from a single apple tree.
= 7 bushels per tree. This means that on average you will get 7 bushels of apples from a single apple tree.- Area =
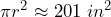 Cost per sq. in. =
Cost per sq. in. = 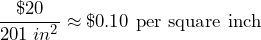
- 12-pack rate =
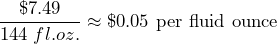
- Every dollar is worth €0.92.
- 400 inches.
 In this section, we will use what we have learned so far to practice skill problems.
In this section, we will use what we have learned so far to practice skill problems.
Skill Exercises
Write the ratio/rate in simplified form:
- 4:5
- 24:60
- 500cm to 300cm
- 6m to 400cm
- 5 feet to 60 inches
- $4 per 100 paper clips
- 320 miles per 16 gallons
- $3.689 for a gallon of gas.
- Write 55 miles per hour as a rate written in fractional form.
- Write the rate
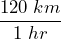 as a speed using per.
as a speed using per.
Show/Hide Answer





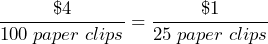 It costs $1 for every 25 paper clips.
It costs $1 for every 25 paper clips.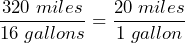 20 miles can be driven on a single gallon of gas.
20 miles can be driven on a single gallon of gas.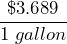
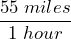
- 120km per hour
the actual measurement of the object
the size of one object compared to the size of another object
a measure of one thing compared to a measure of another thing with the same units; written as a fraction
the first of the two quantities forming a ratio
the second of the two quantities forming a ratio
having no unit of measurement
a comparison of two measures with different units of measurement

