CHAPTER 2: MEASUREMENT

2-5: SI Measurement: Volume and Capacity

Explore Icon Volume Measurement

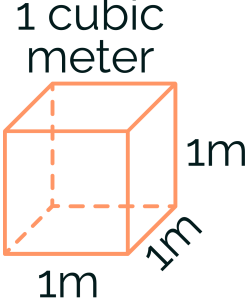Volume is the amount of 3-dimensional space taken up by an object and is measured in cubic units. A cubic centimeter (i.e., 1 cm3)  is a cube with the dimensions 1cm by 1cm by 1cm. So volume = length · width · height = 1cm · 1cm · 1cm = 1cm3. Likewise, a cubic meter (i.e., 1 m3) is a cube with the dimensions 1 m by 1 m by 1 m.

 

 

Explore 1 – Expressing a volume measure

The volume formula for a rectangular solid is Volume = length · width · height. The formula shows the number of cubes in a row times the number of cubes in a column times the number of layers (the height). The result is the number of cubes in a three-dimensional space. For example, a box with length 70 cm, width 50 cm, and height 30 cm has a volume of 70 · 50 · 30 = 105,000 cubes, where each cube has the dimensions 1cm by 1 cm by 1 cm. Since there are 105,000 such cubes in the box, we say the volume is 105,000 cubic centimeters or 105,000cm3.

Find the volume for each of the following spaces:

  1. The size of an official Olympic swimming pool has dimensions of 50 m (length) by 25 m (width) by 2m (depth). Calculate the volume of the Olympic swimming pool.

Solution

Volume = 50 m · 25 m · 2 m = 2500 m3.

  1. The Hoover Dam has approximate dimensions of 379 m (length) by 201 m (width) by 221 m (depth). Calculate the volume of the Hoover Dam.

Solution

Volume = 379 m · 201 m · 221 m = 16,835,559 m3.

  1. How many official Olympic swimming pools can fit into the Hoover Dam? (Round to the hundredth place)

Solution

We need to divide the volume of the dam by the volume of one swimming pool: 16,835,559 m3 ÷ 2,500 m3 = 6734.22 Olympic swimming pools. Note that m3 ÷ m3 = 1; the units cancel each other out.

 

Explore 2 – Basic volume unit conversion

  1. Explain why 1 cm3 = 1,000 mm3. A picture may help you.

Solution

1cm = 10mm, so there are ten 1mm by 1mm by 1 mm cubes on the length and width of the base of a 1cm by 1 cm by 1 cm cube. Consequently, there are 10 · 10 = 100 such unit cubes (i.e., 100 mm2) in the base layer of a 1cm by 1 cm cube. Since there are 10 layers (1 mm per layer), there are 100 · 10 = 1000 1 mm by 1 mm by 1 mm cubes (i.e., 1000 mm3) in a 1 cm by 1 cm by 1cm cube (i.e., 1 cm3).

  1. A 3D printer has a build volume of 400mm by 300 mm by 300 mm. Find the build volume in cubic millimeters, and then convert your answer to cubic centimeters.

Solution

Volume = 400mm · 300mm · 300mm = 36,000,000 mm3. Since there are 10 mm = 1 cm and therefore 1000mm3 = 1 cm3, and we are converting from a smaller to a larger measure of volume, we must divide by 1,000: Volume = 36,000,000 ÷ 1000=36,000 cm3.

 

Reflect Icon

  • What is the meaning of length · width · height for finding the volume of a 3D space?
Show/Hide Answer

The meaning of length and width and height of a region is the number of squares on the longer side (length) and the shorter side (width) and the height of a space. The meaning of length · width · height is the number of squares in a row times the number of squares in a column times the number of layers in order to find the total number of squares in the 3D space.

  • Why do we measure the volume of an object?
Show/Hide Answer

We measure the volume of an object to find the size of an object; the amount of 3-dimensional space it takes up. For example, if we are pouring a new concrete driveway, we need to calculate the volume of the driveway to know how much concrete to order.

 

Practice Exercises

  1. What is an appropriate measure to calculate the volume of a bus?
  2. What is an appropriate measure to calculate the volume of a book?
  3. What is an appropriate measure to calculate the volume of concrete required for a driveway?
  4. What is an appropriate measure to calculate the volume of an aspirin?
  5. A rectangular concrete bollard measures 1.2 meters by 1.2 meters by 0.8 meters. Calculate its volume.
  6. A die is a cube with a side length of 0.8 cm. Calculate its volume.
  7. A book measures 164mm by 128mm by 14 mm. Calculate its volume in cubic centimeters.
Show/Hide Answer
  1. cubic meters
  2. cubic centimeters
  3. cubic meters
  4. cubic millimeters
  5. 1.152 cubic meters
  6. 0.512 cm3
  7. 293.888 cm3

 

Explore Icon Measuring Capacity

Coffee being poured from a flask into a mug

Capacity is the maximum amount that an object can contain. It is the measure of an object’s ability to hold a substance. Capacity and volume are almost the same, but while volume is measured in cubic units, capacity is measured in the base unit liter . The base unit liter is used for measuring capacity in SI along with attached prefixes that make the measurement unit a power of 10 larger or smaller.

The coffee mug takes up space so it has volume. It also has a capacity to hold coffee.

 

Explore 3 – Capacity units

One milliliter dropper One liter bottle of water Tanker of fuel measured in kiloliters

Answer the following questions:

  1. What is an appropriate measure for a cup of tea?

Solution

milliliter

  1. What is an appropriate measure for a tank of fuel?

Solution

liter

  1. What is an appropriate measure for a syringe full of medicine?

Solution

milliliter

  1. What is an appropriate measure for a water reservoir?

Solution

kiloliters

 

Explore 4 – Basic capacity unit conversion

Perform the following capacity unit conversions:

  1. A jar has a capacity of 1200 milliliters. How many centiliters is this?

Solution

The prefix milli is 10 times smaller than centi, so there are 10ml in 1 cl. Therefore, 1200 ml = 1200 · 1 ml = 1200 · (0.1 cl) = 120 cl

  1. A kettle has a capacity of 500 centiliters. How many deciliters is this?

Solution

The prefix centi is 10 times smaller than deci, so there are 10 cl in 1 dl. Therefore, 500 cl = 500 · 1 cl = 500 · (0.1 dl) = 50 dl

  1. A regular bottle of water has a capacity of 500ml. How many liters is this?

Solution

1 l = 1000 ml, so 500 ml is 0.5 l

  1. A tank with volume 1 m3 has a capacity of 1 kl. What is the capacity of a tank with volume 5 m3?

Solution

5 m3 = 5 · 1 m3, so, since a volume of 1 m3 has a capacity of  1kl, 5 m3 has a capacity of 5 · 1 kl = 5 kl

  1. What is the capacity of a spoon that has a volume of 1 cm3.

Solution

1 m3 has a capacity of 1 kl and 1 kl = 1000 l. So 1 m3 has a capacity of 1000 l. Also, 1 m3 = 1 m · 1 m · 1 m = 100 cm · 100 cm · 100 cm = 1,000,000 cm3. And 1 cm3 = 1,000,000 cm3 ÷ 1,000,000, so 1 cm3 has a capacity of 1000 l ÷ 1,000,000 = 0.001 l = 1 ml. Consequently, 1 cm3 = 1 ml.

  1. What is the capacity of a bottle that has a volume of 250 cm3.

Solution

Since 1 cm3 = 1 ml, then 250 cm3 = 250 · 1 cm3 = 250 · 1 ml = 250 ml

 

Reflect Icon

  • What is the difference between volume and capacity, and the units used to measure them?
Show/Hide Answer

Volume is a measure of the amount of 3-dimensional space taken up by an object and is measured in cubic meters. Capacity is a measure of how much substance a 3-dimensional object holds and is measured in liters.

  • What is the relationship between volume and capacity?
Show/Hide Answer

An object with a volume of 1 cubic meter has a capacity of 1 kiloliter. An object with a volume of 1 cubic centimeter has a capacity of 1 milliliter.

 

Practice Exercises

  1. Jane ordered 25 liters of wine for a birthday bash. a) How many milliliters are there in 25 liters?     b) How many glasses of wine are there in 25 l if each glass holds 150 ml.
  2. How many deciliters are there in 450 centiliters?
  3. How many dekaliters are there in 3 kiloliters?
  4. Lana fills a 5 liter water tank to go on a camping trip. How many 250 ml bottles can be filled from a tank of 5 l?
  5. What is the capacity of a wine bottle that has a volume of 750 cm3.
Show/Hide Answer
  1. a) 25,000ml    b) 166 glasses of wine
  2. 45 dl
  3. 300 dal
  4. 20
  5. 750 ml

 

 

In this section, we will take what we have learned and apply the concepts to new situations.

Perspectives

  1. Tankers that carry gas in Europe have a capacity of 16,000 liters across four equal-capacity chambers. How many liters are in each chamber?
  2. An Australian 25 ¢ coin is square and measures 22 mm on each side and is 3 mm thick. Calculate the volume of a stack of 8 coins.
  3. A can of beans measures 8.3 cm in diameter and 12.8 cm high. Cans are packed in boxes 4 cans in length, 3 cans in width, and 2 cans deep. a) What minimum size of box is needed to pack 24 cans? b) What is the volume of the box?
  4. A bento box has a capacity of 1.7 liters. What are possible dimensions of the box if the bottom is square?
  5. Credit and debit cards all have to be the same size of 85.6 mm by 53.98 mm by 0.76 mm. a) Why do credit and debit cards have to be the same size?     b) Calculate the volume of a credit card in cubic centimeters.     c) If you have 5 credit cards in your wallet, how much space are they taking up?
  6. The dimensions of shipping containers have been standardized since 1961. The containers internal width and height are identical at 2.3 meters, while the internal length is either 5.9 meters or 12.03 meters. a) Calculate the capacity of the shorter shipping container.     b) Calculate the capacity of the longer shipping container.
  7. Car engines are often rated by the capacity of their engine cylinders. These used to be measured in cubic centimeters (cc) but are now measured in liters. 1 cubic centimeter of volume has a capacity of 1 milliliter. If a car has a 2.3-liter engine, how many cc’s does it have?
  8. A bottle of water contains 500 ml. A toilet tank has a capacity of 6 liters of water. How many bottles of water are needed to fill a toilet tank? 
  9. Braidy likes to keep her shoes organized in clear plastic shoe boxes that measure 30 cm by 25 cm by 16 cm. a) What is the volume of space taken up by one shoe box?      b) If Braidy has a stack of shoe boxes that is 5 shoe boxes long, 2 shoe boxes deep, and 4 shoe boxes high, what volume of space does this stack take up? 
  10. A box freezer has inside dimensions of 70 cm by 86 cm by 122 cm. What is the capacity of this freezer in liters? 
Show/Hide Answer
  1. 4000 l
  2. 11,616 mm3 = 11.616 cm3
  3. a) 33.2 cm by 24.9 cm by 38.4 cm     b) 31,744.512 cm3
  4.  14 cm by 14 cm by 8.67 cm; 12 cm by 12 cm by 11.81 cm; 10 cm by 10 cm by 17 cm etc.
  5. a) So that all cards fit in ATM and payment machines.      b) about 3.5 cm3      c) about 17.6 cm3
  6. a) 33.2 m3    b) 67.7 m3
  7. 2300 cc
  8. 12 bottles
  9. a) 12,000 cm3     b) 480,000 cm3
  10. 734.44 liters

 

 

Skills IconIn this section, we will use what we have learned so far to practice skill problems.

Skill Exercises

  1. Convert 3 liters to milliliters
  2. Convert 35,000ml to liters
  3. Convert 45kl to l
  4. Convert 6500cl to l
  5. Convert 80,000,000ml to kl
  6. Convert 0.3l to ml
  7. Convert 0.008l to ml
  8. Convert 0.8dal to l
  9. Convert 55,000dl to dal
  10. Convert 280,000ml to kl
Show/Hide Answer
  1. 3000ml
  2. 35l
  3. 45,000l
  4. 65l
  5. 80kl
  6. 300ml
  7. 8ml
  8. 8l
  9. 550dal
  10. 0.28kl

 

 

 

 

definition

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

Numeracy Copyright © 2023 by Utah Valley University is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.