CHAPTER 2: MEASUREMENT
2-7: Dimensions and Dimensional Analysis
Dimensional Analysis
Dimensional analysis is a method for converting between measurement units that uses the fact that any number or expression can be multiplied by one without changing its value. It can handle simple and very complicated measurement unit conversions. Instead of using multiplication or division for unit conversions, as learned in previous sections, dimensional analysis uses fractions that have a numerator and denominator that are equal but in different units. Since the numerator and denominator of the fraction are equal, the fraction is equal to 1. In dimensional analysis, this ratio which converts one unit of measure into another without changing the quantity, is called a conversion factor and is formed by turning equal measures into fractions equal to 1. For example, since 1 ft = 12 in, we can form the conversion factors ![]() or
or ![]() , where each fraction equals 1.
, where each fraction equals 1.
The main idea of performing unit conversions through dimensional analysis, is to multiply by a series of conversion factors equal to 1 where we introduce measurement units we want and cancel out measurement units we don’t want that appear on both the numerator and denominator of different fractions. Dimensional analysis is basically performed in the following way:
![]()
 Dimensional Analysis in the U.S. Customary System
Dimensional Analysis in the U.S. Customary System
Explore 1 – One conversion factor in the U.S. Customary System
- Ashley’s height is 5’6″. Express Ashley’s height in inches. (1 ft = 12 in)
Solution
Since 5’6″ = 5′ + 6″, we can convert 5′ into inches, then add the extra 6 in.
We start by writing 5′ as a fraction over 1: ![]() . This just makes it obvious that the unit feet is on the numerator.
. This just makes it obvious that the unit feet is on the numerator.
This is our starting fraction. Now we want to multiply this by a conversion factor that introduces inches to our numerator and feet to our denominator so that feet will cancel out: ![]()
So,
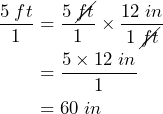
The unit feet cancel out since ![]() .
.
Now we know that 5ft = 60 in, we can add on the remaining 6 in: 5’6″ = 60 in + 6 in = 66 in.
So, Ashley is 66 inches tall.
- The area of a living room is 35 yd2. Express the area in square feet. (1 yd2 = 9 ft2)
Solution
We start with 35 yd2 written as our starting fraction: ![]()
Now we want to multiply this fraction by a conversion factor that introduces square feet to the numerator and square yards to the denominator so that yd2 will cancel out: ![]()
So,
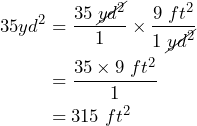
Therefore, 35 yd2 = 315 ft2.
- A medium sized apple weighs about 6 ounces. Express the weight in pounds. (1 lb = 16 oz)
Solution
We start with 6 ounces written as a fraction over 1: ![]()
Now we want to multiply this fraction by a conversion factor that introduces pounds to the numerator and ounces to the denominator so that ounces will cancel out: ![]()
So,
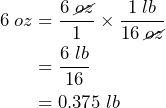
Therefore, 6 ounces = 0.375 pounds.
Explore 2 – Multiple conversion factors in the U.S. Customary System
There may be more than one conversion factor needed in dimensional analysis.
- A standard telephone pole stands about 10 yards tall. Express 10 yards in inches.
Solution
To convert 10 yards to inches, two conversion equations are needed: 1 yd = 3 ft and 1 ft = 12 in. In other words, we will convert from yards to feet, then from feet to inches.
The two conversion factors need to be written in a way that the units yard and feet will be cancelled out with only the ending unit inch left in the dimensional analysis. This means that we need to introduce feet with yards on the denominator so we can cancel out yards in the numerator of the starting fraction: ![]() .
.
We then need to introduce inches on the numerator so that we get to the required end unit, and feet on the denominator so feet can cancel out the feet introduced by the first conversion factor: ![]()
Then,
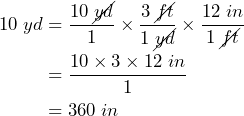
Consequently, a standard telephone pole of 10 yards measures 360 inches tall.
- Express the capacity of a 5-gallon water jug in cups. (1 gallon = 4 quarts, 1 quart = 2 pints, 1 pint = 2 cups)
Solution
We start with 5 gal written as a fraction: ![]() . Then we can convert from gallons to quarts to pints to cups:
. Then we can convert from gallons to quarts to pints to cups:
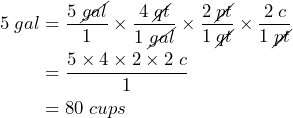
- Express 60 miles per hour in feet per second. (1 mile = 5280 feet, 1 hour = 60 minutes, 1 minute = 60 seconds)
Start by writing 60 miles per hour as a fraction: ![]()
To eliminate miles from the numerator of the starting fraction, we need the conversion factor with miles on the denominator: ![]()
To eliminate hours from the denominator of the starting fraction, we need the conversion factor with hours on the numerator: ![]()
Then to eliminate minutes from the denominator we need minutes on the numerator of a conversion factor: ![]()

Examples
- A bottle of apple juice has 48 fluid ounces. Express this capacity in cups. (1 cup = 8 fl oz)
- The volume of a suitcase is 7560 cubic inches. Express this volume in cubic feet. (1 ft3 = 1728 in3)
- Express 5 pounds of cinnamon in ounces. (1 lb = 16 oz)
- How many tablespoons are in 1 quart of ice cream? (1 fl. oz. = 2 tbsp, 1 cup = 8 fl. oz, 1 pint = 2 cups, 1 quart = 2 pints)
- You are planning a large party. You have invited 150 people and anticipate that 100 people will attend. In preparation, you anticipate that each person will drink around 2 cups of punch that you are providing. How many gallons do you need to purchase to make sure that no one goes thirsty?
- Ground beef costs $4.99 per pound. Express this price in cents per ounce.
Show/Hide Answers
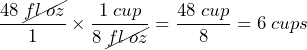 Answer: 6 cups
Answer: 6 cups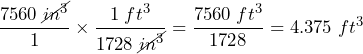 Answer: 4.375 ft3
Answer: 4.375 ft3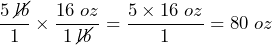 Answer: 80 oz
Answer: 80 oz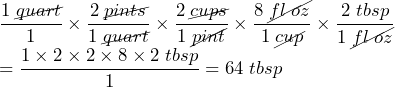 Answer: 64 tablespoons
Answer: 64 tablespoons- 200 cups (
 ) are needed for the 100 anticipated participants.
) are needed for the 100 anticipated participants.
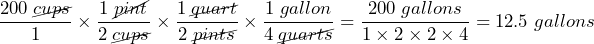 Answer: 13 gallons
Answer: 13 gallons 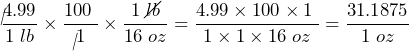 Answer: 31.1875 cents per pound
Answer: 31.1875 cents per pound

- Why do conversion factors like
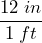 or
or 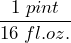 always equal 1?
always equal 1?
Show/Hide Answer
The numerator and denominator of each conversion factor measure the same amount but in different units. So, since the numerator and denominator are equal, they divide to 1.
- How do you determine which unit goes to the numerator or denominator of a conversion factor when doing dimensional analysis?
Show/Hide Answer
If the to-be-eliminated unit is on the numerator of a fraction, it will be in the denominator on the newly introduced conversion factor in dimensional analysis. If the to-be-eliminated unit is on the denominator of a fraction, it will be in the numerator on the newly introduced conversion factor in dimensional analysis.
- Which one is easier, using multiplication/division or using dimensional analysis for unit conversions? Explain your reasoning.
Show/Hide Answer
Answer varies.
Practice Exercises
- Convert 3.5 pounds to ounces using dimensional analysis. (1 lb = 16 oz)
- Convert 7200 fluid ounces to gallons using dimensional analysis. (1 gal = 4 qt, 1 qt = 2 pt, 1 pt = 16 fl. oz.)
- Convert 10,000 steps to miles. (1 step = 2.5 feet, 1 mile = 5280 feet)
- A local steak house has an eating challenge. If you can finish their 72-ounce steak with 3 sides, and an entire pitcher of beer, you get the meal for free. In addition, your picture is put on their wall of fame, AND you get a free t-shirt! How many pounds of steak are 72 ounces?
- Lisa is buying a new rug for her living room that measures 8 feet by 10 feet. Calculate the area of the rug in square inches. (1 ft2 = 144 in2)
- Maria made 5 gallons of soup at the soup kitchen. How many 1-cup ladles of soup is this? (1 gal = 4 qt, 1 qt = 2 pt, 1 pt = 2 cups)
- In February 2023, the average price of gas in Salt Lake City was $3.71 per gallon. What is the cost of gas in cents per pint?
Show/Hide Answers
- 56 oz.
- 56.25 gal
- 4.7 miles
- 4.5 lb
- 11,520 in2
- 80 cups
- 46.375 cents per pint
 Dimensional Analysis in SI
Dimensional Analysis in SI
Explore 3 – One conversion factor using SI
1. Jenny’s height is 1.83 meters. Convert 1.83 meters to centimeters. (1m = 100 cm)
Solution
We start by writing 1.83m as a fraction over 1: ![]()
Since meters is on the numerator of the starting fraction, our conversion factor must have meters on the denominator so that meters cancel out: ![]()
![]()
So, Jenny’s height is 183cm.
2. The diameter of a quarter coin is about 2.3 centimeters. Convert 2.3 centimeters to millimeters. (1 cm = 10 mm)
Solution
We start by writing 2.3 cm as a fraction over 1: ![]()
Since centimeters is on the numerator of the starting fraction, our conversion factor must have centimeters on the denominator so that centimeters cancel out: ![]()
![]()
The diameter of a quarter is about 23 mm.
3. A typical can of soda holds 355 milliliters. How many cans would be equivalent to a 2-liter bottle of soda? (1 liter = 1000 milliliter)
Solution
We need to convert bottles to cans so we start by writing 1 bottle as a fraction over 1: ![]()
Since bottle is on the numerator of the starting fraction, our conversion factor must have bottle on the denominator so that bottle cancels out: ![]()
![]()
So, it would take 5.63 cans of soda to be equivalent to a 2-liter bottle of soda.
4. A stick of butter weighs 113 grams. How many kilograms is the stick of butter? (1 kg = 1000 g)
Solution
Our starting fraction is ![]() . The conversion factor is therefore,
. The conversion factor is therefore, ![]() .
.
![]()
So, a stick of butter weighs 0.133 kg.

- True or False: There is no need to use multiple conversion factors for unit conversions using SI. Explain your reasoning.
Show/Hide Answer
Some people may say “False” because multiple conversion factors may be generated in the Metric System. For example, the two conversion factors ![]() and
and ![]() may be generated to convert 5 km to centimeters.
may be generated to convert 5 km to centimeters.
However, some people may say “True” because the unit conversion between any two units may be represented by one conversion factor because of the decimal number system of the metric system. For example, only the conversion factor ![]() is needed for converting 5 km to centimeters.
is needed for converting 5 km to centimeters.
Practice Exercises
- A package weighs 45,800 grams. Use dimensional analysis to convert this weight to kilograms.
- Teapots come in different sizes but a common size is 1.5 liters. Use dimensional analysis to convert this capacity to milliliters.
- The world’s longest water slide measures 1111 meters long[1]. Use dimensional analysis to convert this length to kilometers.
- El Injerto coffee beans are some of the rarest in the world and sell for around $500 for 450 grams. Use dimensional analysis to convert this to dollars per kilogram.
- Mall walking is a form of exercise where people walk or jog through the usually long corridors of shopping malls before the stores open. Gertie meets up with a group of mall walkers most mornings to get in her recommended 10,000 steps. If her step measures about 65 cm, what is the minimum distance Gertie walks in meters around the mall? Is this more or less than a kilometer?
Show/Hide Answers
- 45.8 kg
- 1500 ml
- 1.111 km
- $1111.11 per kg
- 6500 m = 6.5 km This is more than 1 km.
The origins of dimensional analysis have been disputed by historians with the first written application of dimensional analysis credited to an article by François Daviet at the Turin Academy of Science in 1799[2]. The modern use of dimensional analysis, which distinguishes mass, length, and time as fundamental units, while referring to other units as derived, was primarily established by James Clerk Maxwell, a Scottish mathematician and scientist, around 1873[3]. Commensurable physical quantities are of the same kind and have the same dimension, and can be directly compared to each other, even if they are expressed in different units of measure, e.g. yards and meters, pounds and kilograms, seconds and years. For example, the length of a dollar bill is the same whether it is measured as 6.14 inches or 156 mm.
 Dimensional Analysis Across Systems
Dimensional Analysis Across Systems
NASA has been notorious for having problems due to one team using SI units and the other team using U.S. Customary units. In 1998, NASA lost equipment worth millions of dollars thanks to shoddy conversion practices. SOHO, the Solar Heliospheric Observatory lost all communications with Earth for a week due to a mix up between U.S. and metric measures. The following year, NASA lost a Mars Orbiter worth $125 million for similar reasons. Nowadays, all scientific endeavors are calculated using the metric system. This includes all medications, after an order was misread and 0.5 grams of Phenobarbital (a sedative) were given to a patient instead of 0.5 grains (only 0.0325 grams)! Consequently, it is vital that if different systems are used conversions are accurate, and rounding errors are avoided.
Explore 4 – One conversion factor across systems
To convert between measuring systems, equivalent measures need to be known across systems. Some equivalent measures are exact, like 1 inch = 2.54 cm, while others are approximate, like 1 yard ≅ 0.91 meters.
 1. The longest tail ever recorded on a dog was 76.8 cm. It belongs to an Irish Wolfhound named Keon who lives in Belgium[4]. How long is Keon’s tail in inches? (1 inch = 2.54 cm)
1. The longest tail ever recorded on a dog was 76.8 cm. It belongs to an Irish Wolfhound named Keon who lives in Belgium[4]. How long is Keon’s tail in inches? (1 inch = 2.54 cm)
Solution
We start with 76.8cm written as a fraction: ![]() .
.
The conversion factor needs cm on the denominator so cm will cancel: ![]()
Then,
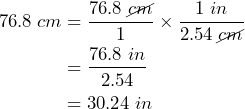
Keon’s tail measures 30.24 inches.
2. How many liters can a 5-gallon jug hold? (1 gallon = 3.7854 liters)
Solution
We start with 5 gal written as a fraction: ![]() .
.
The conversion factor needs gallons on the denominator so they will cancel: ![]()
Then, 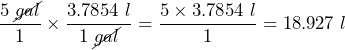
A 5-gallon jug can hold 18.927 liters.
3. How many gallons are equivalent to 2-liters of soda? (1 gallon = 3.7854 liters)
Solution
We start with 2 liters written as a fraction: ![]() .
.
The conversion factor needs liters on the denominator so they will cancel: ![]()
Then, ![]()
0.53 gallons is equivalent to 2 liters.
4. A typical can of soda holds 355 milliliters. How many cups can the can hold? (1 cup = 236.588 milliliters)
Solution
We start with 355ml written as a fraction: ![]() .
.
The conversion factor needs ml on the denominator so they will cancel: ![]()
![]()
A 355ml can of soda is equivalent to 1.5 cups.
Explore 5 – Multiple conversion factors across systems
Perform the following unit conversions using dimensional analysis. Round your answers to the nearest hundredths place.
1. Ting brings her nephews to an amusement park in Taiwan. A sign at the entrance of the Roller Coaster says the minimum height to ride is 150 centimeters. One of her nephews is 5-feet tall. Is her nephew tall enough to ride the Roller Coaster? Explain your reasoning. (1 ft = 12 in, 1 in = 2.54 cm).
Solution
We need to convert 5 feet into cm. We will start with the fraction ![]() and use the conversion factors
and use the conversion factors ![]() and
and ![]() .
.
![]()
Yes, he is tall enough to ride since 5 feet = 152.4cm and 152.4cm > 150cm.
2. The hotel room you booked in Paris is 21.2 m2, according to their website. How many square feet is the room? Is this room large or small? Explain your reasoning. (1m2 = 10,000 cm2, 1 in2 = 6.4516 cm2, 1 ft2 = 144 in2)
Solution
We need to convert square meters to square feet. We start with the fraction ![]() .
.
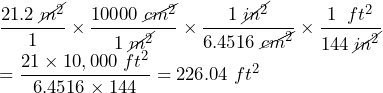
226.04 ft2 is a room that is approximately 15 feet by 15 feet, which is a smaller size for a hotel room.
3. How many liters is equivalent to a quart of icecream? (1 gallon = 4 quarts, 1 gallon = 3.7854 liters)
Solution
We need to convert from quarts to liters. We start with the fraction ![]() .
.
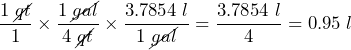
A quart of icecream s equivalent to 0.95 liters.
4. How many cups can a 2-liter soft drink bottle hold? (1 liter = 1000 milliliter, 1 cup = 236.588 milliliters)
Solution
We need to convert from liters to cups. We start with the fraction ![]() .
.
![]()
A 2-liter bottle can hold 8.45 cups.
Practice Exercises
- A medium pizza in Europe measures 30 cm. What is this measurement in inches? (1 inch = 2.54cm)
- The average size of a U.S. hotel room is 300 square feet. What is this area in square meters? (1m2 = 10,000 cm2, 1 in2 = 6.4516 cm2, 1 ft2 = 144 in2)
- The average house size in the U.K. is 76 square meters[5]. What is this area in square feet? (1 m2 = 10,000 cm2, 1 in2 = 6.4516 cm2, 1 ft2 = 144 in2)
- The height of a net stretched across a tennis court varies in height from 3 ft 6 in. at the posts to 3 feet at the center of the net. Convert these measurements to centimeters. (1 ft = 12 in, 1 in = 2.54 cm)
Show/Hide Answers
- 11.8 inches
- 27.87 square meters
- 818 square feet
- 3 ft 6 in = 106.68 cm and 3 ft = 91.44 cm
 Temperature Conversions
Temperature Conversions
The US measures temperature in degrees Fahrenheit while the rest of the world uses degrees Celsius. We cannot use dimensional analysis to convert from Celsius to Fahrenheit and vice versa since there is no unit conversion factor. Instead, we use a formula:
Temperature Conversion Formulas
Fahrenheit = 1.8 Celsius + 32 or ![]()
Celsius = (Fahrenheit – 32) ÷ 1.8 or ![]()
Explore 6
- While traveling in Spain, Emily notices a sign that shows the temperature as 32° C. What is the temperature in Fahrenheit?

Solution
In the formula ![]() , we replace
, we replace ![]() with 32 then use order of operations to evaluate for
with 32 then use order of operations to evaluate for ![]() .
.
![]()
32°C is equivalent to 89.6°F.
- Your favorite cooking blog has a new cookie recipe! It lists the temperature for baking the cookies at 375° F. What is that temperature in Celsius?
Solution
In the formula ![]() we replace
we replace ![]() with 375 then use order of operations to evaluate for
with 375 then use order of operations to evaluate for ![]() .
.
![]()
375°F is equivalent to 190.6°C.
Practice Exercises
- At the Women’s World Cup in 2019, France recorded extremely high temperatures that reached up to 45° C. Convert this temperature to Fahrenheit.
- Ted and his friends are on their way to Jasper National Park in Canada to camp. He worries his sleeping bag may not be warm enough, so he stops by a sports store in Calgary and picks one up with a temperature rating of 10°C. This means that an average person should be warm enough if the temperature drops to around 10°C. His friends tell him he must choose one that is 10°C warmer than the listed rating (i.e., 10°C lower than the listed rating). Ted’s friend says the temperature at night may drop to as low as 35°F. Will the sleeping bag Ted picks be warm enough? Explain your reasoning.
Show/Hide Answers
- 113°F
- 35°F = 1.7°C A sleeping bag rated at 10°C may not be warm enough (1.7°C < 10°C). Ted’s friends are correct, he should buy a bag rated to 0°C.

- In the US, fuel economy is measured in miles per gallon. The 2023 V-6 Ford Bronco averages 17 mpg.
- a) What exactly does this rate tell us?
- b) Convert this rate to gallons per 100 miles
- c) At today’s gas prices, what would it cost to travel 100 miles?
- In Canada, fuel economy is measured in liters per 100 km, and the 2023 Ford Bronco’s window sticker reads 13.9 liters per 100 km.
- a) What exactly does this rate tell us?
- b) Convert this rate to gallons per 100 miles.
- c) Do the U.S. and Canadian fuel economy measures match up?
- d) Which fuel economy measure would you prefer to see on car window stickers? Miles per gallon or gallons per mile? Explain your reasoning.
 In this section, we will take what we have learned and apply the concepts to new situations.
In this section, we will take what we have learned and apply the concepts to new situations.
Perspectives
-
- The tallest building in the world is the Burj Khalifa in the U.A.E. at a staggering 828 meters tall. This compares to the tallest building in the U.S. which is One World Trade Center at 1776 feet tall. How many feet taller than One World Trade Center is Burj Khalifa? [6]
- A microwave oven built in Europe measures 76.2cm by 53.3cm by 63.5cm. a) Calculate the volume of the microwave in cubic centimeters. b) Convert this volume to cubic inches.
- The rocket that Space X sent into orbit was traveling 7 miles per second when it left the atmosphere. Convert the speed of the rocket to miles per hour.
- Ben and Jerry need to order mulch for their yard. They have calculated that the area they need to cover is 400 ft2. They want the mulch to measure a depth of 3 inches. a) Calculate the volume of mulch they will need in cubic feet. b) Convert this volume to cubic yards. c) They can have mulch delivered in 1 yd3 bags to their home. How many bags should they order?
- On a European vacation you notice a speed limit of 150 km per hour. Convert this to miles per hour.
- Gas prices in Scotland in early 2023 averaged 1.49 British Pounds per liter. What is this price in dollars per gallon? (1 BP = $1.23, 1 gal = 3.78541 liters)
- In February 2023, the price of beef in Switzerland was 51.50 CHF (Swiss Francs) per kilogram. What is this price per pound in US dollars? (1kg = 2.2 lb, 1 CHF = $1.08)
- Carpet Heaven has carpet for $3 per square foot. a) Convert this price to the cost per square yard. b) Floorings R Us has the same carpet for $25 per square yard. Which store is cheaper?
- You are going to lay sod in your backyard. Based upon your measurements, your backyard is about 8000 square feet. Sod is sold in 1 square yard rolls. How many rolls of sod do you need to purchase?
- The most valuable substance on earth is Botulinum toxin which is used to create Botox. It values at $1.5 trillion per kg. In each shot of Botox, there are 0.73 ng of Botulinum toxin. What is the value of the toxin in each shot of Botox?
- A microwave oven built in Europe measures 76.2cm by 53.3cm by 63.5cm. a) Calculate the volume of the microwave in cubic centimeters. b) Convert this volume to cubic inches.
- A gallon of gasoline weighs about 6.3 pounds. A gasoline tank for a sedan car holds about 15 gallons. What is the weight of the gasoline in the tank if the tank is full?
- Is a 0.75 ton horse heavier than a 738 kg camel? (1 ton = 2000 pounds, 1kg = 2.20462 pounds).
- Your kitten is sick and your vet prescribes medicine. You need to give your kitten 550mg of medicine every 8 hours for the next 10 days. The medicine is only sold in 225mg tablets. A bottle of 24 tablets sells for $32.95. How many bottles of medicine will you need to buy and how much will it cost you?
- Aconcagua is the highest peak in South America, with a height of 6961 meters. Convert this height to feet. (1 mile = 1.60934)
- On a vacation to Scotland, you notice that petrol (gasoline) is priced in pounds per liter. If petrol costs £1.43 per liter, what does it cost in dollars per gallon? Assume £1 = $1.28.
Show/Hide Answers
- The Burj Khalifa is 2716.54 feet tall, which is 940.54 feet taller than One World Trade Center.
- a) 257,902.71cm3; b) 15,738.189 in3
- 25,200 mph
- a) 100 ft3 b) 3.7 yd3 c) 4 bags
- 93 mph
- $6.94 per gallon
- a) $21.68 per lb.
- a) $27 per yd2, b) Floorings R Us
- 2667 rolls
- $1.095 per shot
- 257,902.71cm3
- 94.5 lb
- Horse weighs 680.4kg which is less than a 738kg camel.
- 3 bottles which will cost $98.85.
- 22,838 ft.
- $6.93 per gallon
 In this section, we will use what we have learned so far to practice skill problems.
In this section, we will use what we have learned so far to practice skill problems.
Skill Exercises
Convert the measurements using dimensional analysis:
- 4500 milliliters to liters
- 3.5 gallons to cups
- 34.8 kg to grams
- 56,000 mg to kg
- 88,000,000 cm to km
- 3,500,000,000 cm2 to square meters
- 25 fl. oz. to milliliters
- 3600 cubic inches to liters
- 3600 fl. oz. to gallons
- 100 square yards to square meters
- 25 square meters to square yards
- $5.60 per pound to cents per ounce
- 40 mph to meters per second
- $0.15 per milliliter to $ per liter
- $2.99 per pint to $ per gallon
Show/Hide Answers
- 4.5 liters
- 56 cups
- 34,800 grams
- 0.056 kg
- 880 km
- 350,000 m2
- 739.33824ml
- 58.99343 liters
- 28.125 gallons
- 83.6127m2
- 29.8998 yd2
- 35 cents per ounce
- 17.88 meters per second
- $150 per liter
- $23.92 per gallon
- Longest water slide ↵
- Origin of dimension analysis ↵
- Roche, John J (1998). The Mathematics of Measurement: A Critical History, Springer, p. 203, ISBN 978-0-387-91581-4 ↵
- Longest dog tail ↵
- Average house size in the United Kingdom ↵
- Guiness book of records ↵
a method for converting between measurement units
a ratio of different measurement units that is equal to one
calculation errors due to inexactness in the representation of real numbers and the arithmetic operations done with them

