CHAPTER 2: MEASUREMENT
2-1: U.S. Customary System of Measurement: Length and Area
The U.S. Customary System of Measurement
Every object in this world has size. Describing size requires units of measurement. It is important to communicate clearly, so measurement units are required to give accurate descriptions of objects. Consequently, measurement has been around for about as long as mankind. An immediately obvious tool for measuring objects is our body (e.g., hand, foot) and this was how the British system of measurement was first developed; a foot was the length of the King’s foot, for example. Guess what happened when the King died! To beat that dilemma, measurement units were standardized in 1824 and became the Imperial system of measurement so that a foot is the same measure wherever we are in the world. The measure hand was originally the length spanned by 4 fingers but was standardized to 4 inches. Today hand is still used to measure the height of horses from the ground to their withers. So a horse that is 16 hands high, measures 16 · 4 inches = 64 inches from level ground to its withers. Currently, all but three countries use the base 10 metric system as their standard system of measurement, while the United States, Myanmar, and Liberia continue to use systems based on the old Imperial system. In the U.S., the Imperial system morphed into the U.S. Customary System of Measurement. As people do business or cultural exchanges around the world, measurement conversions become necessary, though in the scientific world the S.I. system (metric) is now the standard.
The next three sections will help us recognize and differentiate units of the U.S. Customary System of Measurement. If you grew up in the United States, this is the system you are familiar with. We will explore measures of length, area, volume, capacity, and weight and consider which units are used to measure different objects.
 Length Measurement
Length Measurement
Length is a one-dimensional measure of how long something is. Measurements are based on unit measures (e.g., 1 inch). 5 inches is equivalent to adding 5 measures of 1 inch. So, 5 inches = 1 inch + 1 inch + 1 inch + 1 inch + 1 inch. Since multiple additions of the same number is defined as multiplication, 5 inches = 5 times the length of 1 inch. So, 5 inches = 5 · 1
Examples
- Write 6 feet as a multiple of 1 foot.
- Write 6 feet as the addition of 1-foot measures.
Show/Hide Answer
-
- 6 feet = 6
 1 foot
1 foot - 6 feet = 1 foot + 1 foot + 1 foot + 1 foot + 1 foot + 1 foot
- 6 feet = 6
A ruler or a measuring tape is used to measure the length of an object in feet and inches. Each foot is divided into 12 inches, and typically each inch is divided into 16 parts, each measuring 1/16th of an inch. Slightly longer bars are shown every 1/4 inch and 1/2 inch to make measuring easier.

Fractions and mixed numbers are used to measure a length that lies between a whole number of units. For example, 1/2 inch or ![]() inches. Mixed units are also used in the U.S. System. For example, the height of a person is typically measured in feet and inches (e.g., 5 feet 11 inches). Although it is not technically correct since we are not using base 10, measurements are also seen in everyday life using decimal points (e.g., 22.5 inches). We just have to remember that
inches. Mixed units are also used in the U.S. System. For example, the height of a person is typically measured in feet and inches (e.g., 5 feet 11 inches). Although it is not technically correct since we are not using base 10, measurements are also seen in everyday life using decimal points (e.g., 22.5 inches). We just have to remember that ![]() inches.
inches.
Due to the size of objects, different units of length were developed. The unit yard is used for measuring lengths of fabrics and textiles, football fields and golf courses. The unit mile is used for measuring the distance between two places (e.g., between cities/towns and between countries).
Measures of Length
1 mile = 1760 yards = 5280 feet
1 yard = 3 feet
1 foot = 12 inches
Abbreviations are often used for measurement units. The abbreviation for foot is ft or ![]() (, while inch is in or
(, while inch is in or ![]() (called double prime). So a measure of 3 feet 4 inches can be written 3 ft 4 in or
(called double prime). So a measure of 3 feet 4 inches can be written 3 ft 4 in or ![]() . Likewise, yd is used for yard and mi for mile.
. Likewise, yd is used for yard and mi for mile.
Explore 1 – Length
- What is an appropriate unit to measure the height of a coffee table?
Solution
Coffee tables are relatively short so inches are most appropriate.
- What is an appropriate unit to measure the width of a golf green?
Solution
Golf greens are measured in yards.
- What is an appropriate measure to measure the distance from Orem to Salt Lake City?
Solution
Distance between cities is measured in miles.
- What is the length of the pencil?

Solution
The length of the pencil is ![]() inches.
inches.
- How tall is a horse that measures 14 hands 3 inches?
Solution
14 hands = 14 · 4 inches = 56 inches, so 14 hands 3 inches = 56 inches + 3 inches = 59 inches.
- What is the length of your right foot?
- Use a measuring tape to measure your height. Write your height in feet and inches.
Explore 2 – Length unit conversion
Kenji is thinking of upgrading his bed. His bedroom measures 10 feet by 12 feet and he would love a king-size mattress. A king-size mattress measures 76 inches wide and 80 inches long. Determine if a king-size mattress can fit into the room nicely and leave enough space for other furniture (e.g., a desk, a couch, or a closet). Use unit conversion to convert between inches and feet. Explain your reasoning. A drawing may help.
Solution
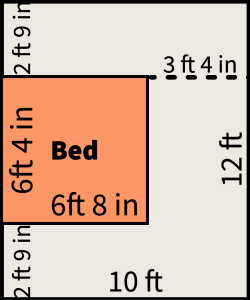 We need to get both measurements into the same unit. We can choose to either convert the room dimensions into inches or convert the bed dimensions into feet.
We need to get both measurements into the same unit. We can choose to either convert the room dimensions into inches or convert the bed dimensions into feet.
Converting all dimensions into feet:
Since 1 foot = 12 inches, to convert from inches to feet we need to know how many units of 12 inches divide into each dimension. ![]() and
and ![]() . So the bed measuring 6 ft 4 in by 6 ft 8 in will fit into the 10 ft by 12 ft room. Since it is typical to leave approximately 3 feet on three sides of the bed, the remaining space in the room may be ok for a small desk (e.g., 3 ft by 2 ft) or a chair. It may not be enough for larger furniture such as a couch and/or a closet. It also depends on the location of doors and windows.
. So the bed measuring 6 ft 4 in by 6 ft 8 in will fit into the 10 ft by 12 ft room. Since it is typical to leave approximately 3 feet on three sides of the bed, the remaining space in the room may be ok for a small desk (e.g., 3 ft by 2 ft) or a chair. It may not be enough for larger furniture such as a couch and/or a closet. It also depends on the location of doors and windows.
Alternatively, converting all measurements into inches:
10 feet = 10 · 1 foot = 10 · 12 inches = 120 inches and 12 feet = 12 · 1 foot = 12 · 12 inches = 144 inches. So the room measures 120 inches by 144 inches.
6 ft 4 in = 6 · 1 ft + 4 in = 6 · 12 in + 4 in = 72 in + 4 in = 76 in and 6 ft 8 in = 72 in + 8 in = 80 in. So the bed measures 76 in by 80 in.
So the bed 76 in by 80 in will fit into the room 120 inches by 144 inches.

- How do fractions or mixed numbers help us express a measure of length?
Show/Hide Answer
Fractions and mixed numbers can help express a measure that is not a whole number of units long.
- Explain how to convert feet into inches?
Show/Hide Answer
Multiply the number of feet by 12 inches per foot.
- Explain how to convert inches into yards?
Show/Hide Answer
Since there are 12 inches in a foot and 3 feet in a yard, there are 12 · 3 = 36 inches in a yard. So, we divide the number of inches by 36 inches per yard.
Practice Exercises – Length
- What is an appropriate unit to measure a foot race?
- What is an appropriate unit for measuring the height of a tree?
- Write 4 yards as a multiple of 1 yard.
- Write 3 miles as the addition of 1-mile measures.
- Determine the radius of the largest circle that can be inscribed inside a 4 feet 6 inch square.
- Determine the height in feet and inches of someone who is 69 inches tall.
- Determine the dimensions of a lawn in yards (and feet) that measures 100 feet by 68 feet.
- The front door on Steve’s house measures 2 yards 1 foot 6 inches by 1 yard 2 feet. Determine the dimensions in inches.
Show/Hide Answer
-
- yards or miles
- feet
- 4 yards = 4 · 1 yard
- 3 miles = 1 mile + 1 mile + 1 mile
- A circle with a radius of 2 feet 3 inches.
- 5 feet 9 inches
- 33 yards 1 foot by 22 yards 2 feet
- 90 inches by 60 inches
 Area Measurement
Area Measurement
 Area is a measure of the amount of space inside a two-dimensional object. For example, a square that has dimensions of 1 inch by 1 inch has an area of 1 square inch or 1 in2. A square that has dimensions of 1 foot by 1 foot has an area of 1 square foot or 1 ft2. A square that has dimensions of 1 yard by 1 yard has an area of 1 square yard or 1 yd2. A square that has dimensions of 1 mile by 1 mile has an area of 1 square mile or 1 mi2. In general, a square that measures 1 unit by 1 unit has an area of 1 unit2 and is referred to as a unit square.
Area is a measure of the amount of space inside a two-dimensional object. For example, a square that has dimensions of 1 inch by 1 inch has an area of 1 square inch or 1 in2. A square that has dimensions of 1 foot by 1 foot has an area of 1 square foot or 1 ft2. A square that has dimensions of 1 yard by 1 yard has an area of 1 square yard or 1 yd2. A square that has dimensions of 1 mile by 1 mile has an area of 1 square mile or 1 mi2. In general, a square that measures 1 unit by 1 unit has an area of 1 unit2 and is referred to as a unit square.
Examples
- What is an appropriate measurement unit to describe the area of a painting?
- What is an appropriate measurement unit to describe the floor space of a home?
- What is an appropriate measurement unit to describe the area of a parking lot?
Show/Hide Answer
- Square inches
- Square feet
- Square yards
Explore 3 – Measuring Area
The area of a rectangle is calculated by multiplying its length by its width: ![]() . The formula shows the number of unit squares in a row (suppose this is the length) times the number of unit squares in a column (suppose this is the width). The result is the number of unit squares in a two-dimensional region. For example, a rectangle with a length measuring 10ft and a width of 5ft has an area of
. The formula shows the number of unit squares in a row (suppose this is the length) times the number of unit squares in a column (suppose this is the width). The result is the number of unit squares in a two-dimensional region. For example, a rectangle with a length measuring 10ft and a width of 5ft has an area of ![]() unit squares where each square has the dimension 1 foot by 1 foot. Since there are fifty unit squares, we say the area is 50 square feet or 50 ft2.
unit squares where each square has the dimension 1 foot by 1 foot. Since there are fifty unit squares, we say the area is 50 square feet or 50 ft2.
First estimate and then calculate the exact area for each object:
- A linen tablecloth that has the dimensions 59″ by 78″.
Solution
Estimate: rounding to the nearest ten, Area = length ![]() width
width ![]() 60″
60″ ![]() 80″ = 4800 in2.
80″ = 4800 in2.
Exact: Area = length ![]() width = 59 in
width = 59 in ![]() 78 in = 4602 square inches.
78 in = 4602 square inches.
- A rectangular parking lot that measures 235 yards by 358 yards.
Solution
Estimate: rounding to the nearest hundred, Area = length ![]() width
width ![]() 200 yd
200 yd ![]() 400 yd = 80,000 yd2.
400 yd = 80,000 yd2.
Exact: Area = length ![]() width = 235 yd
width = 235 yd ![]() 358 yd = 84,130 yd2.
358 yd = 84,130 yd2.
- A living room carpet that has the dimensions
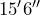 by
by 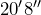 .
.
Solution
Estimate: rounding to the nearest ten feet, Area = length ![]() width
width ![]() 20 ft
20 ft ![]() 20 ft = 400 ft2.
20 ft = 400 ft2.
Exact: With mixed measurements involving feet and inches, we can write inches as a fraction of a foot. ![]() , so
, so ![]() .
.
Likewise, ![]() , so
, so ![]() .
.
Since Area = length ![]() width, the area of the carpet is
width, the area of the carpet is ![]() square feet.
square feet.
 To enter a mixed measurement into a calculator, use the fraction key
To enter a mixed measurement into a calculator, use the fraction key ![]() .
.
For example, ![]() can be entered as
can be entered as 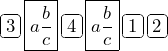
To calculate an area that measures ![]() by
by ![]() we enter:
we enter:

The result is 49.583… square feet or ![]() square feet.
square feet.
Explore 4 – Basic area unit conversion
- Explain why 1 yd2 = 9 ft2. Draw a picture to help you.
Solution

There are three 1 foot by 1 foot squares on each side of a square that is 1 yard by 1 yard (or 1yd2). Therefore, there are ![]() unit squares (i.e., 9 ft2) in a 1 yard by 1 yard square (1yd2).
unit squares (i.e., 9 ft2) in a 1 yard by 1 yard square (1yd2).
- Explain why 1 ft2 = 144 in2. Draw a picture to help you.
Solution
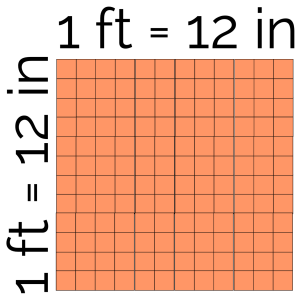
There are twelve 1 inch by 1 inch squares on each side of a square that is 1 foot by 1 foot (or 1yd2). Therefore, there are ![]() unit squares (i.e., 144 in2) in one square foot (1 ft2).
unit squares (i.e., 144 in2) in one square foot (1 ft2).
- Some stores measure linens in square feet. Convert your answer for the first question of explore 3 into square feet. (Round your answer to the square foot)
Solution
Since there are 144 square inches in a square foot, we divide our answer by 144 to convert from square inches to square feet: ![]() ft2.
ft2.
- Some carpet stores use square yards rather than square feet when measuring carpets. Convert your answer for the second question of Explore 3 into square yards. (Round your answer to the nearest square yard)
Solution
Since there are 9 ft2 in a square yard, we divide our answer by 9 to convert from square feet to square yards: ![]() yd2.
yd2.
- A floor has dimensions
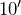 by
by 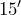 . Dave plans to tile the floor with tiles that measure
. Dave plans to tile the floor with tiles that measure 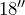 by
by 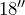 . How many tiles does Dave need to cover the floor? If the tiles come in boxes of twelve tiles, how many boxes should he buy?
. How many tiles does Dave need to cover the floor? If the tiles come in boxes of twelve tiles, how many boxes should he buy?
Solution
Since there are two different measurement units in play (feet and inches), we need to either convert the tile measurements to feet or the floor measurements to inches. The dimensions of the floor in inches are ![]() inches by
inches by ![]() inches. Therefore, the area of the floor is
inches. Therefore, the area of the floor is ![]() square inches. The area of a single tile is
square inches. The area of a single tile is ![]() square inches. We need to know how many times the area of a single tile divides into the area of the floor:
square inches. We need to know how many times the area of a single tile divides into the area of the floor: ![]() . Dave needs to buy at least 67 tiles to cover the floor. Since there are 12 tiles to a box, Dave needs
. Dave needs to buy at least 67 tiles to cover the floor. Since there are 12 tiles to a box, Dave needs ![]() boxes.
boxes.
Notice that we will always round up in this type of situation. For example, here 5 boxes would supply 5 · 12 = 60 tiles, which is not enough. 6 boxes will supply 6 · 12 = 72 tiles, which is too many. However, it is always better to have too many tiles in case of breakage or other human errors.

- Explain why measurement units for area have the word square in them.
Show/Hide Answer
The word square describes a real square of length 1 unit on each side of the square. Area is a measure of the number of unit squares that fit inside a two-dimensional shape. When length and width are multiplied, the units are also multiplied. So, unit · unit = square unit.
Practice Exercises –Area
- Estimate then calculate the exact area of a tv screen that measures 32 inches by 57 inches.
- Carry-on bags for airlines in the U.S. are limited to 22 inches long, 14 inches wide and 9 inches high including wheels and handles. Calculate the area of the front (or back) of such a bag.
- An area rug measures
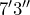 by 5
by 5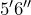 . Calculate the area of the rug in square feet.
. Calculate the area of the rug in square feet. - A dining table measures 84 inches by 42 inches. Calculate the area of the table top in square inches. Convert your answer to square feet.
- A rectangular driveway measures 18 feet by 34 feet. Calculate the area of the driveway in square feet. Convert your answer to square yards.
Show/Hide Answers
- Estimate: Area = 1800 square inches Exact: Area = 1824 square inches
- Area = 308 square inches
- Area =
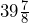 square feet
square feet - Area = 3528 square inches =
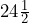 square feet
square feet - Area = 612 square feet = 68 square yards
 In this section, we will take what we have learned and apply the concepts to new situations.
In this section, we will take what we have learned and apply the concepts to new situations.
Perspectives
-
- Perimeter is the total distance around an object. Calculate the perimeter of a rectangle that has sides of length 3 feet 4 inches and 2 feet 9 inches.
- The circumference of a circle can be found by multiplying its diameter by
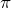 . Calculate the circumference to 2 decimal places of a circular jar lid that has a diameter of 8 inches.
. Calculate the circumference to 2 decimal places of a circular jar lid that has a diameter of 8 inches. - A truck tire has a radius of 10.5 inches. How far will the truck travel in one revolution of the tire? Round to the nearest inch.
- A queen size mattress measures 60 inches by 80 inches. Calculate the sleeping area of a queen size mattress.
- The area of a triangle can be found by multiplying the length of its base by its height, then dividing by 2. A triangular tortilla chip measures 1 ½ inches along its base and is 2 inches high. What is the area of the top of the tortilla chip?
- A sailboat has a sail that is a right triangle that measures 18 feet by 5 feet. What is the area of the sail?
- An international basketball court measures 92 feet long by 49 feet wide. Calculate the area of a court in square yards. Round to the nearest tenth.

Wash Day and Wind by Robert Aswani. - The main square in the center of Mexico City is the Zócalo, which measures 300 yards by 300 yards. Calculate the area of the Zócalo.
- A prayer rug measures
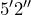 by
by 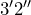 . Calculate the area of the rug.
. Calculate the area of the rug. - The painting Wash Day and Wind by contemporary Kenyan artist Robert Aswani measures
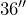 by
by 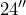 . What is the area of the painting?
. What is the area of the painting?
Show/Hide Answers
- 12 ft 2 in
- 25.13 in
- 66 in
- 4800 in2
- 1.5 in2
- 45 ft2
- 500.9 yd2
- 90,000 yd2
- 16.36 ft2
- 864 in2 or 6 ft2
 In this section, we will use what we have learned so far to practice skill problems.
In this section, we will use what we have learned so far to practice skill problems.
Skills Practice
Calculate the perimeter:
- A square that measures 7.4 inches on each side.
- A rectangle that measures 4 ft 2 in by 6 ft 3 in.
- A circle that has a diameter of 6 yards.
- A semi-circle with a radius of 8 feet.
Show/Hide Answer
- 29.6 in
- 20 ft 10 in
- 18.85 in
- 41.13 ft
Calculate the rectangular area with dimensions:
- 2 ft by 7 ft
- 7 in by 9 in
- 3 miles by 8 miles
- 4 ft 5 in by 8 ft 3 in
- 9 yd 2 ft by 7 yd 1 ft
Show/Hide Answer
- 14 ft2
- 63 in2
- 24 mi2
- 36.4375 ft2 or 5247 in2
- 70.89 yd2 or 638 ft2
Convert:
- 3 lb 6 oz to ounces
- 25,000 lb to tons
- 4 yd to inches
- 2 yd 1 ft to inches
- 500 inches to feet
- 8 square feet to square inches
- 320 square feet to square yards
- 1 square mile to square yards
- 3 cubic yards to cubic feet
- 9.5 cubic feet to cubic inches
Show/Hide Answer
- 54 oz
- 12.5 tons
- 144 in
- 84 in
- 41.67 ft or
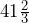 ft
ft - 1152 in2
- 35.56 yd2 or
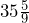 yd2
yd2 - 3,097,600 yd2
- 81 ft3
- 16,416 in3
The system of measurement used in the United States of America
a measured distance in one dimension
having length but no width or height
the amount of space inside a two-dimensional object measured in square units
having length and width but no depth
a square that measures 1 unit by 1 unit
a mathematical relationship or rule expressed in symbols

