CHAPTER 1: NUMBER SENSE
1-7 The Relationship Between Fractions and Decimals
Fractions and Decimals
There are many ways of expressing a quantity in our daily life. For example, any measure of length may be expressed in terms of a fraction (e.g., 1/2 inch bolt) or a decimal number (e.g., 2.5 meter long rug). Time can be measured using fractions (e.g., one-quarter of an hour). When writing a check, the number of cents is written in fraction form (e.g., two hundred fifty & 27/100 dollars). Gas prices are often shown in a mix of decimals and fractions. There is a relationship between fractions and decimals that needs to be explored.
 Relationship between Fractions and Decimals
Relationship between Fractions and Decimals
It’s important to remember that fractions are just numbers. They are numbers that help fill in the spaces between integers on a number line. Fractions can be positive as well as negative, and the set of all fractions is called the set of rational numbers, denoted by the letter ![]() for quotient.
for quotient.
Explore 1 – Fractions and their equivalent terminating decimals
Use simplified fractions and decimals to express the quantity in terms of a dollar:
- one quarter
Solution
One quarter is equivalent to 25¢ = $0.25, and ![]() . Since 25¢ is
. Since 25¢ is ![]() of a dollar, that is why a 25¢ coin is called a quarter. This means that the fraction
of a dollar, that is why a 25¢ coin is called a quarter. This means that the fraction ![]() is equivalent to the decimal 0.25.
is equivalent to the decimal 0.25.
- one dime
Solution
One dime is equivalent to 10¢ = $0.10, and ![]() . So, the decimal 0.1 is equivalent to the fraction
. So, the decimal 0.1 is equivalent to the fraction ![]() .
.
- one cent
Solution
One cent = 1¢ = $0.01, and ![]() . So, the fraction
. So, the fraction ![]() is equivalent to the decimal 0.01.
is equivalent to the decimal 0.01.
- 20 cents
Solution
20 cents = 20¢ ![]() and 20¢ = $0.20. So, the fraction
and 20¢ = $0.20. So, the fraction ![]() is equivalent to the decimal 0.2.
is equivalent to the decimal 0.2.
- 60 cents
Solution
60 cents = 60¢ = $0.60, and ![]() . So, the fraction
. So, the fraction ![]() is equivalent to the decimal 0.6.
is equivalent to the decimal 0.6.
- 75 cents
Solution
75 cents = 75¢= $0.75 and ![]() . So, the fraction
. So, the fraction ![]() and the decimal 0.75 are equivalent.
and the decimal 0.75 are equivalent.
 To simplify a fraction, input the fraction into your calculator using the fraction key then press enter.
To simplify a fraction, input the fraction into your calculator using the fraction key then press enter.
For example, to simplify ![]() input
input 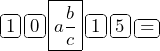
The result is ![]()
![]() and
and ![]() are equivalent fractions.
are equivalent fractions.
Explore 2 – Fractions and their equivalent terminating decimals
When fractions are improper they represent numbers greater than or equal to 1. It is often useful to write these improper fractions as mixed numbers. Mixed numbers consist of an integer + a proper fraction. For example, ![]() is a mixed number equivalent to
is a mixed number equivalent to ![]() .
. ![]() is also equivalent to
is also equivalent to ![]() as an improper fraction, and as 3.5 as a decimal.
as an improper fraction, and as 3.5 as a decimal.
Write the mixed numbers shown at each arrow on the measuring tape as improper fractions and their equivalent decimals.

Solutions
Terminating decimals always have equivalent fractions and are therefore rational numbers.
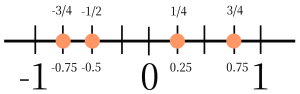
Figure 1. Fractions and equivalent decimals.
 To convert between fractions and terminating decimals,use the
To convert between fractions and terminating decimals,use the ![]() button (F = fraction and D = decimal) that sits above the
button (F = fraction and D = decimal) that sits above the ![]() button (PRB = probability) and converts between fractions and decimals.
button (PRB = probability) and converts between fractions and decimals.
For example, to determine the equivalent decimal for the fraction ![]() the input is:
the input is:
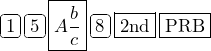
The result is:
![]()
So, ![]()
The same result is obtained by treating the fraction bar as a division sign. So, ![]() .
.
The calculator input is:
![]()
To convert 1.645 to a fraction, the input for a calculator is:
![]()
The result is ![]() .
.
Alternatively, we can recognize that there are 3 decimal places after the point in 1.645 so the 5 is in the thousandths place. This means that we can write the fraction as ![]() , then simplify it to
, then simplify it to ![]() .
.
The calculator input is:
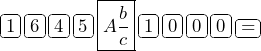
 To convert between mixed numbers and improper fractions, use the button
To convert between mixed numbers and improper fractions, use the button 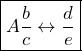 that sits above the
that sits above the ![]() button and converts between mixed numbers and improper fractions.
button and converts between mixed numbers and improper fractions.
For example, to convert ![]() to an improper fraction, the calculator input is:
to an improper fraction, the calculator input is:
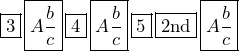
The result is ![]() .
.
To convert ![]() to a mixed number, the calculator input is:
to a mixed number, the calculator input is:
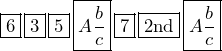
The result is ![]() .
.
Explore 3 – Fractions and their equivalent non-terminating repeating decimals
In business, a share of profits is a common way of rewarding investors. Five investors receive 1/3, 1/6, 1/7, 1/9, and 1/11 of the 2022 profits respectively.
- Use the fractions to determine the share of the profit each investor receives if the 2022 profit is $100 million.
Solution
Using a calculator, we multiply each fraction by $100 million. The shares are $33,333,333.33; $16,666,666.67; $14,285,714.29; $11,111,111.11; $9,090,090.09 respectively.
- What did you round your answer to? Explain your reasoning.
Solution
Rounded to the nearest cent since less than one cent is meaningless in terms of money earned.
- Use your calculator to turn these fractions into decimals.
Solution
Using a calculator, the equivalent decimals are:
![]()
![]()
![]()
![]()
![]()
- Do you notice any patterns with the decimals?
Solution
Each decimal has repeating (or recurring) decimal digits. The recurring digits have a horizontal bar above them.
- How many decimal places should be used to calculate the profit for each investor if the 2022 profit is $100 million? Explain your reasoning.
Solution
It depends on how the payments are rounded. If we want numbers to the nearest dollar we would have to round each decimal to at least the hundred millionths place. This is because the hundred-millionth place (i.e., 10-8) after being multiplied by 100 million (i.e., 108), will result in an answer to the ones place (dollar). If we want the precision to be at the hundredth place (cent) after multiplying by 100 million (i.e., 108), then the decimal places should go down to ten-billionth place (i.e., 10-10).
- Use the decimals to determine the share of the profit each investor receives.
Solution
Investor 1 receives $33,333,333.33. Investor 2 receives $16,666,666.67. Investor 3 receives $14,285,714.29. Investor 4 receives $11,111,111.11. Investor 5 receives $9,090,909.09.
- Is there any difference in the results from using fractions or decimals?
Solution
No, because the correct number of decimal places were used to calculate the shared profits. If we rounded the decimal to say 2 decimal places, the investors would have lost a great deal of money. For example, investor 1 would have received $33,000,000 instead of $33,333,333.33, which is a loss of $333,333.33.
- If we were to first round each decimal obtained from the fractions to the hundredth place, is there a difference in the results from using the fraction?
Solution
Yes. The shared profits would then be $33 million; $17 million; $14 million; $11 million; and $9 million respectively. This is called rounding error.
Recurring decimals always have equivalent fractions and are therefore rational numbers.

- How do you know if a fraction has an equivalent recurring decimal? In other words, what kind of denominators result in a recurring decimal? Show your ideas and explain your reasoning.
Show/Hide Answer
A simplified fraction has an equivalent recurring decimal if its denominator has a prime factor other than 2 or 5 will have a repeating decimal representation.
- What situations lend themselves better to decimals than fractions?
Show/Hide Answer
Any time we are using a base 10 system. For example, when money is involved or we are using the metric system of measurement.
- What situations lend themselves better to fractions than decimals?
Show/Hide Answer
Any time we are using a base that is not 10. For example, in the U.S. Customary System of measurement.
- Are there any decimals that cannot be written as fractions?
Show/Hide Answer
Yes. Fractions result in equivalent decimals that are either terminating or recurring. So any decimal that never terminates and never recurs cannot be written as a fraction.
 Operations on Fractions Using a Calculator
Operations on Fractions Using a Calculator
Explore 4 – Using a calculator to perform operations on fractions
- Calculate
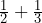 using your calculator, then use partitioning to explain why the denominator of the result is 6, not 5. Show your reasoning.
using your calculator, then use partitioning to explain why the denominator of the result is 6, not 5. Show your reasoning.
Solution
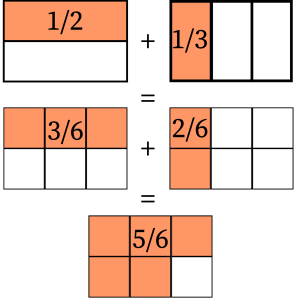
The two fractions cannot be added unless both of them are under the same number of equally partitioned parts (the common denominator). Six is a common multiple of 2 and 3. It is also the common number of equally partitioned parts with ![]() and
and ![]() . Therefore, the sum of the two fraction is
. Therefore, the sum of the two fraction is ![]() .
.
- Perform the operation
 using your calculator, then use partitioning to explain why the denominator of the result is 12, not 7. Show your reasoning.
using your calculator, then use partitioning to explain why the denominator of the result is 12, not 7. Show your reasoning.
Solution
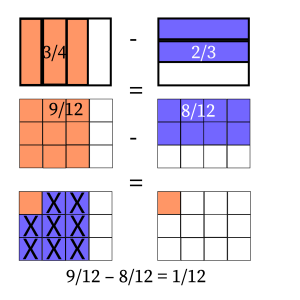
The two fractions need to be converted into equivalent fractions with the same denominator (the same number of equally partitioned parts) so that they may be added under the same measure. Twelve is a common multiple of 3 and 4. The equivalent fractions are ![]() and
and ![]()
Therefore, the difference of the two fractions is ![]() .
.
- Perform the operation
 using your calculator. Why do you think the result is not a fraction? Explain your reasoning (use partitioning).
using your calculator. Why do you think the result is not a fraction? Explain your reasoning (use partitioning).
Solution
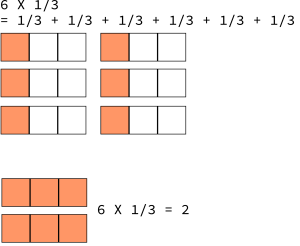
The number 6 may be divided into three equal parts (e.g., 2+2+2). The operation ![]() means “1/3 of 6”, or, one of the three parts 6 is partitioned into. Therefore,
means “1/3 of 6”, or, one of the three parts 6 is partitioned into. Therefore, ![]() , an integer.
, an integer.
- Perform the operation
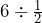 using your calculator. Why do you think the result is larger than 6? Explain your reasoning (use partitioning).
using your calculator. Why do you think the result is larger than 6? Explain your reasoning (use partitioning).
Solution
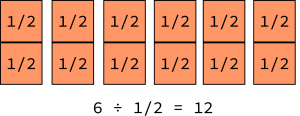 6 divided by 1/2 means how many halves are needed to make 6? One can be split into 2 halves, so 12 can be split into 6 · 2 = 12 halves. Therefore,
6 divided by 1/2 means how many halves are needed to make 6? One can be split into 2 halves, so 12 can be split into 6 · 2 = 12 halves. Therefore, ![]() .
.
Explore 5 – Using a calculator to perform operations on fractions
Fatma’s baby drank ![]() then
then ![]() of a bottle of milk today. The capacity of the baby bottle is 8-fluid ounces. How many fluid ounces did the baby consume?
of a bottle of milk today. The capacity of the baby bottle is 8-fluid ounces. How many fluid ounces did the baby consume?
Solution
Use the fraction button ![]() to add the fractions using your calculator.
to add the fractions using your calculator.
Input: 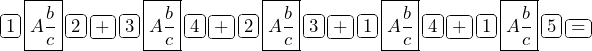
Now multiply by 8 to determine how many fluid ounces are in ![]() bottles.
bottles.
Continued Input: ![]()
The result is ![]() fluid ounces.
fluid ounces.
To turn this into a decimal we continue the calculator input as ![]() and the result is 10.933333333…ounces or
and the result is 10.933333333…ounces or ![]() ounces.
ounces.
The baby drank approximately 10.9 fluid ounces of milk.

- Is it true that the denominator of the result after adding or subtracting fractions is always a common multiple of the denominators of the fractions?
Show/Hide Answer
Yes, it is true. Fractions cannot be added unless they are using the same base, which means equivalent fractions must be found with the same denominator for each fraction. They must be added or subtracted when they are partitioned into the same number of equal parts.
- If a positive integer is divided by a fraction, is it true that the result is always greater than the positive integer?
Show/Hide Answer
No. The result will be less than the positive integer if the positive integer is divided by a fraction that is greater than 1.
Practice Exercises
- You decide to track your productivity in a planner and account for every ¼ of an hour. At the end of the day, you track 9 quarter hours where you did nothing but scroll on your phone. How many hours did you end up scrolling? Write your answer as a mixed number.
- The Official Federal Dietary Guidelines[1] recommend eating no more than 2300 mg (i.e., one teaspoon) of table salt per day. Eric’s mom usually puts 1/3 teaspoon of salt in each dish of food she makes and 1/2 teaspoon of salt in a pot of soup. There were three dishes and one soup for today’s dinner. Eric ate about one quarter of each dish and
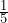 th of the soup. How many teaspoons of salt did Eric consume?
th of the soup. How many teaspoons of salt did Eric consume? - Dr. Park announces the results of a mathematics test. She is very happy because ¾ of the students scored at least 80 out of 100, with half of those scoring 100. There are 32 students in her class. How many students scored 100?
- The table shows the recommended feeding guide in cups for adult dogs of all breeds. I have a 30-pound Sheepdog and a 60-pound Labrador.
Recommended Feeding Guide for Adult Dogs
| Weight | Daily Amount |
|---|---|
| 5 lbs | 1/2 |
| 10 lbs | 7/8 |
| 15 lbs | 1 1/8 |
| 20 lbs | 1 1/2 |
| 30 lbs | 2 |
| 40 lbs | 2 1/2 |
| 60 lbs | 3 1/4 |
| 80 lbs | 4 |
| 100 lbs | 4 3/4 |
Increase feeding intake by 1/2 cup for every 20 lbs over 100 lbs.
Feeding instructions (Using standard 8 oz measuring cup)
- a) How many cups of food do my dogs eat every day if I feed them the recommended amount?
- b) I am considering fostering a 120-pound Great Pyrenees. How much extra food will I need each week?
Show/Hide Answers
 hours
hours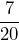 teaspoons
teaspoons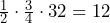 students
students- a)
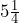 pounds b)
pounds b) 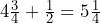 pounds per day
pounds per day 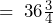 pounds per week.
pounds per week.
 In this section, we will take what we have learned and apply the concepts to new situations.
In this section, we will take what we have learned and apply the concepts to new situations.
Perspectives
- The Rum Runner cocktail from the Florida Keys has 10 ingredients:

ice
1 fluid ounce pineapple juice
1 fluid ounce orange juice
1 splash grenadine syrup
1 slice orange
![]() fluid ounce blackberry liqueur
fluid ounce blackberry liqueur
![]() fluid ounce banana liqueur
fluid ounce banana liqueur
![]() fluid ounce light rum
fluid ounce light rum
![]() fluid ounce dark rum
fluid ounce dark rum
![]() fluid ounce high-proof rum
fluid ounce high-proof rum
- a) Calculate how many fluid ounces of rum is in this cocktail.
- b) Calculate how many fluid ounces of alcoholic liquor is in this cocktail.
- c) How many more fluid ounces of blackberry liqueur than banana liqueur are in this cocktail?
- d) How many total fluid ounces are in this cocktail?
- Deborah’s SUV gets about 21 miles for every gallon of gas. Her gas tank holds 18 gallons.
- a) About how many miles can Deborah travel on a full tank of gas?
- b) About how many miles can Deborah travel on a
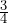 tank of gas?
tank of gas? - c) About how many miles can Deborah travel on a
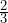 tank of gas?
tank of gas? - d) About how many miles can Deborah travel according to her fuel gauge?

Show/Hide Answers
- a)
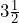 fluid ounces of rum. b)
fluid ounces of rum. b) 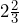 fluid ounces. c)
fluid ounces. c) 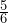 fluid ounces. d)
fluid ounces. d) 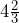 fluid ounces
fluid ounces
- a) 378 miles. b) 283.5 miles. c) 252 miles. d) 94.5 miles
 Irrational Numbers
Irrational Numbers
Numbers that can be written as a fraction or ratio of two integers are called rational numbers. So, when it came time to name numbers that cannot be written as a fraction of two integers, they were called irrational numbers. As far back as the 7th century B.C.E. Indian mathematicians accepted the existence of irrational numbers. The first number ever to be proved irrational was √2 by the ancient Greeks around the 5th century B.C.E. The symbol √ is referred to as a radical sign and is read ‘square root’. In fact, all square roots of natural numbers (except perfect squares) are irrational. Together, the rational and irrational numbers form the set of real numbers.
A quick history of pi
The constant pi (denoted by the greek letter ![]() ) is another example of an irrational number. Calculating a decimal approximation for this number has been a worldwide affair starting with ancient civilizations around 2000 B.C.E., including the Egyptians and Babylonians, who used approximations for
) is another example of an irrational number. Calculating a decimal approximation for this number has been a worldwide affair starting with ancient civilizations around 2000 B.C.E., including the Egyptians and Babylonians, who used approximations for ![]() of 3.1605 and 3.125 respectively. Around 250 B.C.E. the Greek mathematician Archimedes created an algorithm that calculated
of 3.1605 and 3.125 respectively. Around 250 B.C.E. the Greek mathematician Archimedes created an algorithm that calculated ![]() to be a number between 3.140845 and 3.142857. By the 5th century Chinese mathematicians approximated
to be a number between 3.140845 and 3.142857. By the 5th century Chinese mathematicians approximated ![]() to 7 decimal places (3.1415926) but it wasn’t until 1400 that an Indian mathematician discovered
to 7 decimal places (3.1415926) but it wasn’t until 1400 that an Indian mathematician discovered ![]() to 10 decimal places. Surprisingly, the earliest known use of the Greek letter
to 10 decimal places. Surprisingly, the earliest known use of the Greek letter ![]() to represent this constant was by a Welsh mathematician in 1706. Today
to represent this constant was by a Welsh mathematician in 1706. Today ![]() has been calculated beyond
has been calculated beyond ![]() decimal places with the use of computers.[2]
decimal places with the use of computers.[2]
Definition of pi

![]() is defined as the ratio of the circumference of a circle to its diameter. But since
is defined as the ratio of the circumference of a circle to its diameter. But since ![]() is irrational that ratio cannot contain two integers.
is irrational that ratio cannot contain two integers. ![]() is a constant that is a non-repeating, never ending decimal number. It is found on most calculators, making working with
is a constant that is a non-repeating, never ending decimal number. It is found on most calculators, making working with ![]() very straightforward.
very straightforward.
Explore 6
![]() is defined as the ratio of a circle’s circumference to its diameter:
is defined as the ratio of a circle’s circumference to its diameter: ![]() = circumference/diameter
= circumference/diameter
This can be rearranged to Circumference = ![]() diameter or, as a formula,
diameter or, as a formula, ![]()
- If you key in
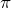 to your calculator, what do you get?
to your calculator, what do you get?
Solution
3.141592653589793 depending on the number of digits displayed by your calculator
- Why is
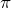 an irrational number?
an irrational number?
Solution
![]() is irrational because it cannot be written as a fraction. It is a non-terminating, non-repeating decimal number.
is irrational because it cannot be written as a fraction. It is a non-terminating, non-repeating decimal number.
- Calculate the circumference of a vinyl record with a diameter of 30 centimeters. Round your answer to the nearest tenth.
Solution
Circumference = ![]() Diameter =
Diameter = ![]() 30 centimeters = 94.247… centimeters
30 centimeters = 94.247… centimeters ![]() 94.2 centimeters.
94.2 centimeters.
Explore 7
The area of a circle can be calculated using the formula: Area = ![]() (radius)2 or
(radius)2 or ![]()
 What unit of measurement will the area of a manhole cover be measured in? Explain your reasoning.
What unit of measurement will the area of a manhole cover be measured in? Explain your reasoning.
Solution
Since ![]() , the units will be
, the units will be ![]() or square centimeters.
or square centimeters.
- Calculate the area of a circular manhole cover that has a radius of 17 inches. Round your answer to the nearest square centimeter.
Solution
![]() square centimeters
square centimeters
- Why are manhole covers typically round?
Solution
So they can’t fall into the hole they cover.
Practice Exercises
The volume of a sphere can be calculated using the formula: Volume = ![]() (radius)3 or
(radius)3 or ![]()
 What units will the volume be measured in? Explain your reasoning.
What units will the volume be measured in? Explain your reasoning.- The Higo Chumbo fruit (prickly pear) is approximately round with a radius of 5 cm. Calculate the volume of a Higo Chumbo fruit. Round your answer to the nearest tenth.
- Calculate the diameter and volume of a standard basketball with circumference 74.9 cm. Round your answers to the nearest tenth.
Show/Hide Answers
- Volume uses radius3 so the units will be centimeters3 or cubic centimeters.
- Volume = 523.598… cubic centimeters =
 523.6 cm3.
523.6 cm3. - Radius = 22.9 cm; Volume = 50,303.1 cm3.
 In this section, we will use what we have learned so far to practice skill problems.
In this section, we will use what we have learned so far to practice skill problems.
Skill Exercises
Simplify the fractions:
1. ![]() 2.
2. ![]() 3.
3. ![]() 4.
4. ![]() 5.
5. ![]()
Evaluate:
6. ![]()
7. ![]()
8. ![]()
9. ![]()
10. ![]()
11. ![]()
12. ![]() .
.
13. ![]()
14. ![]() .
.
15. ![]()
16. ![]()
17. ![]()
18. ![]()
19. ![]()
20. ![]()
21. ![]()
22. ![]()
23. ![]()
Show/Hide Answers
The set of all numbers that can be written as fractions using whole numbers.
the answer obtained by dividing one number by another number
a fraction where the numerator and denominator have no common factors other than 1
fractions that have different numerators and denominators but are equal to the same value
an integer + a proper fraction
decimals with a finite number of digits; decimals that stop
the horizontal line separating the numerator from the denominator in a fraction
calculation errors due to inexactness in the representation of real numbers and the arithmetic operations done with them
decimals where a number or a group of numbers repeat over and over an infinite number of times
the answer when one quantity is added to another quantity
the answer when one quantity is subtracted from another quantity
numbers that cannot be written as a fraction of two integers
a symbol for the square root or higher-order root of a number
numbers that have a whole number square root
The set of rational numbers combined with the set of irrational numbers.
the distance around a circle
the length of the line through the center of the circle that touches two points on the edge of the circle


