1-6: Number Sense with Fractions

Hazel McKenna; Leo Chang; Roxanne Brinkerhoff

CHAPTER 1: NUMBER SENSE

1-6: Number Sense with Fractions

Fractions

Most things in life do not fit into an integer world. We may use integers for counting whole items like people or objects, but decimals are used for money or anything else that requires a fractional part. Place values to the right of the decimal point represent the fractional parts of tenths, hundredths, thousandths, etc. If we are working with metric measurements like meters, decimal fractions are commonplace. For example, 1 centimeter is one-hundredth of a meter. That is, 1 centimeter = 0.01 meters. But when we are working in the U.S. Customary System of measurement, we have equivalencies like 1 foot = 12 inches and 1 yard = 3 feet; we are no longer working with a base 10 system. This is where fractions come into play to represent part of a whole in any base we wish to work in. For example, knowing that 1 foot = 12 inches, tells us that we are working in base 12. Since there are 12 inches in a foot, we can say that 1 inch is one-twelfth of a foot. Using fractions, we have 1 inch = $\dfrac{1}{12}$ foot. The denominator (bottom number) of a fraction tells us the base we are working in, while the numerator (top number) tells us how many parts of the base we are dealing with. Likewise, since 1 yard = 3 feet, we can say that 1 foot = one-third of a yard. That is, 1 foot = $\dfrac{1}{3}$ yards. When we are working with feet and yards we are working in base 3.

What is a Fraction?

In the U.S. school, system children start learning about fractions in the 3rd grade. They are introduced visually as parts of a whole. The uniqueness of fractions is that we can divide a whole into any number of pieces we wish and that is what makes fractions so useful. Those who understand fractions may not even notice them. But to the fractionally-impaired, they can be a constant nuisance.

Explore 1 – Proper Fractions

The key to understanding fractions is knowing that a whole is split into equal parts, and that the number of equal parts makes up the denominator of the fraction. The word denominator comes from the latin dēnōminātor and simply means that which names. In this case we are naming the base of the fraction.

The numerator of a fraction tells us how many of the equal parts described in the denominator are being counted. The word numerator comes from the latin numerus, which means number. In this case we are stating how many equal parts have been used.

State the fraction shown in each visualization.

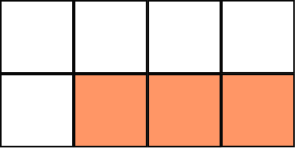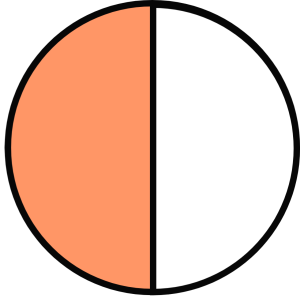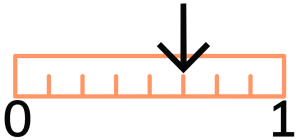1. 8 equal squares with 3 squares colored 2. circle solit into 2 equal parts with 1 part colored. 3. Ruler with 0 to 1 split into 8 equal parts. Arrow at 5th part. 4.

Solutions

There are 8 equal parts so the denominator is 8. Three parts are colored orange, so 3 is the numerator of the fraction representing the orange part of the whole: $\dfrac{3}{8}$ . Also, 5 parts are colored white, so the white fraction is $\dfrac{5}{8}$ . Notice that the orange part plus the white part combines to the whole: $\dfrac{3}{8}+\dfrac{5}{8}=1$ .

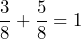There are 2 equal parts and 1 is colored orange: $\dfrac{1}{2}$ . There is also one part colored white, so the white fraction is $\dfrac{1}{2}$ . The orange part plus the white part combines to the whole: $\dfrac{1}{2}+\dfrac{1}{2}=1$ .

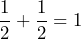The whole from 0 to 1 is partitioned into 8 equal parts. The arrow is at the 5th equal part: $\dfrac{5}{8}$

The whole from 0 to 1 is partitioned into 10 equal parts. The line is at the 9th equal part: $\dfrac{9}{10}$

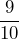
Explore 2 – Improper Fractions

Fractions that have a numerator less than the denominator are called proper fractions. They represent parts of a whole. But fractions also exist that are greater than or equal to 1. In this case the numerator is greater than or equal to the denominator. Fractions that are greater than or equal to 1 are called improper fractions.

State the fraction shown in each visualization. Determine if the fraction is proper or improper.

1. Two squares cut into 4 equal parts. One square all 4 parts are colored. The other square 3 parts are colored. 2. Two whole split into 5 equal parts. 5 parts are chosen on the first whole. 1 part is chosen on the second whole. 3.

4. Line measured by ruler where each unit is split into 4 equal parts. Line starts at zero and goes to one part past 5.

Solutions

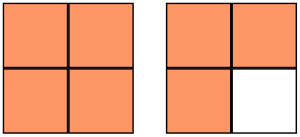
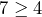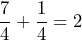Each whole square is divided into 4 equal parts, so the denominator is 4. The total number of colored parts is 7: $\dfrac{7}{4}$ . Since $7\ge 4$ this is an improper fraction. Also, the white square that is left represents the fraction $\dfrac{1}{4}$ , which is a proper fraction. Notice that $\dfrac{7}{4}+\dfrac{1}{4}=2$ because the orange part combined with the white part gives us two whole units.

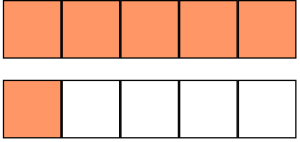
Each rectangle is divided into 5 equal parts, so the denominator is 5. The total number of colored parts is 6, so the numerator is 6: $\dfrac{6}{5}$ Since 6 ≥ 5 this is an improper fraction. The white squares form the fraction $\dfrac{4}{5}$ , which is proper. In addition, the orange fraction + the white fraction = 2 wholes: $\dfrac{6}{5}+\dfrac{4}{5}=2$ .

The rectangle is divided into 3 equal parts, so the denominator is 3. The total number of colored parts is 3, so the numerator is 3: $\dfrac{1}{3}$ . Since 1 < 3 this is a proper fraction. The remaining white part is denoted by the fraction $\dfrac{2}{3}$ , which is also proper. Notice that the orange fraction + the white fraction = 1 whole: $\dfrac{1}{3}+\dfrac{2}{3}=1$

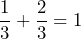
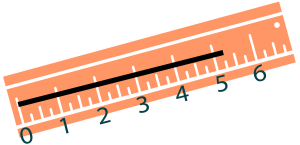
The distance between each whole number is split into 4 equal parts, so the denominator is 4. The black line starts at 0 and ends at 1 part past 5, so 21 equal parts have been used (i.e., 5 · 4 + 1 = 21). So, the fraction is 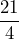$\dfrac{21}{4}$ . Since 21 ≥ 4 this is an improper fraction.

How is the denominator of a fraction determined?

Show/Hide Answer

The denominator is determined by the number of equal parts that make up the whole.

How is the numerator of a fraction determined?

Show/Hide Answer

The numerator is determined by the number of equal parts that are chosen.

What is the difference between a proper fraction and an improper fraction?

Show/Hide Answer

A proper fraction is a fraction that is less than one, with the numerator less than the denominator. An improper fraction is a fraction that is at least one, with the numerator greater than or equal to the denominator.

Number Sense and Relative Size

Number sense not only applies to decimals, it applies to all types of numbers including fractions. Number sense is an extension of common sense and can help us compare the relative size of fractions with no operations involved.

Explore 3 – Relative size of fractions

Answer the following questions using number sense (i.e. without using a calculator). Often a drawing can help.

Fatma’s baby drank $\dfrac{1}{2}$ , and then $\dfrac{3}{4}$ of a bottle of milk. Did the baby drink more than one bottle of milk? Explain your reasoning.

Solution

If we split a whole into 4 equal parts to get quarters, then $\dfrac{4}{4}=1$ and $\dfrac{2}{4}=\dfrac{1}{2}$ . This means that $\dfrac{3}{4}$ is greater than $\dfrac{1}{2}$ . Since two halves make one whole, $\dfrac{1}{2}+\dfrac{1}{2}=1$ , so $\dfrac{1}{2}+\dfrac{3}{4}>1$ . Yes, the baby drank more than one bottle of milk.

The baby then drank another $\dfrac{2}{3}$ of a bottle of milk. Did the baby drink more than two bottles of milk so far?

Solution

The drawing shows that if we split the bottle of milk into quarters, we can visualize adding 1/4 to each of the other two bottles. The 1/4 bottle and the 3/4 bottle combine to a whole bottle, but the 1/4 bottle added to the 2/3 bottle doesn’t quite make a full bottle. No, the baby did not drink more than two bottles of milk.

In other words, $\dfrac{1}{4}+\dfrac{3}{4}=1$ , and since $\dfrac{1}{4}<\dfrac{1}{3}$ (splitting a whole into 4 equal parts results in a part than is smaller than a part formed by splitting a whole into 3 equal parts), and since $\dfrac{1}{3}+\dfrac{2}{3}=1$ , then $\dfrac{1}{4}+\dfrac{2}{3}<1$ .

Did you notice that $\dfrac{1}{4}+\dfrac{3}{4}=1$ ? If we turn this into a subtraction, this means that $1-\dfrac{3}{4}=\dfrac{1}{4}$ .

Likewise, $\dfrac{1}{2}+\dfrac{1}{2}=1$ , so $1-\dfrac{1}{2}=\dfrac{1}{2}$ .

Explore 4 – Relative size of fractions

Answer the following questions using number sense (i.e. without using a calculator).

Esther gives her mom her math test sheet weekly. For the last month, Esther’s grades in chronological order were 4/5, 5/6, 6/7, and 7/8. Are Esther’s grades improving? Explain your reasoning.

Solution

Yes, Esther’s grades are improving. One whole may be partitioned into equal parts of 5, 6, 7, or 8. The distances away from 1 for the fractions 4/5, 5/6, 6/7, and 7/8 are 1/5, 1/6, 1/7, and 1/8, respectively. Since $\frac{1}{5}>\frac{1}{6}>\frac{1}{7}>\frac{1}{9}$ , the distance away from 1 for the fraction 1/5 is greater than 1/6. The distance away from 1 for the fraction 1/6 is greater than 1/7. The distance away from 1 for the fraction 1/7 is greater than 1/8. Therefore, $\frac{7}{8}>\frac{6}{7}>\frac{5}{6}>\frac{4}{5}$ .

Explore 5 – Relative size

Determine which weight is heavier: $\dfrac{5}{8}$ pounds or $\dfrac{2}{3}$ pounds.

Solution

One way to compare fractions is by partitioning a whole into an equal number of parts that accommodates both values of the denominator. We can do this in two ways: 1) use the product of the denominators, or 2) use any number both denominators divide into exactly.

In this case $8\times3=24$ . 8 and 3 both divide into 24 exactly.

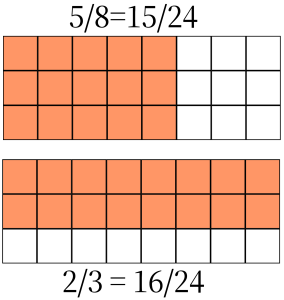
graphic showing 5/8=15/24 and 2/3=16/24

Since 16 > 15, $\dfrac{15}{24}>\dfrac{16}{24}$ . Consequently, $\dfrac{2}{3}$ pounds is heavier than $\dfrac{5}{8}$ pounds .

Since $\dfrac{5}{8}=\dfrac{15}{24}$ , $\dfrac{5}{8}$ and $\dfrac{15}{24}$ are equivalent fractions.

Since $\dfrac{2}{3}=\dfrac{16}{24}$ , $\dfrac{2}{3}$ and $\dfrac{16}{24}$ are equivalent fractions.

Reflect Icon

How would you compare the size of two fractions (e.g., 2/3 and 3/4) using the method of partitioning?

Show/Hide Answer

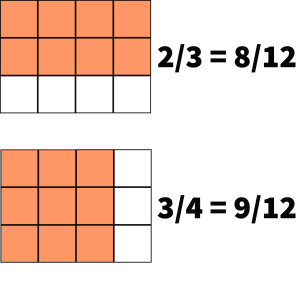Partitioning 1 into 12 equal parts, where the number 12 is the multiple of 3 and 4. Then identify the size of 2/3 (i.e., 8/12) and the size of 3/4 (i.e., 9/12) from the 12 equal parts. Since 9/12 > 8/12, this means that 3/4 > 2/3.

Using number sense, how would you compare the size of two fractions when their numerators are the same but their denominators are not (e.g., 7/8, 7/11)?

Show/Hide Answer

When two fractions have the same numerator but different denominators such as 7/8 and 7/11, the fraction with a smaller denominator is larger because the fraction with a smaller denominator has larger sized parts (i.e., 1/8 > 1/11) according to partitioning. Therefore, 7/8 > 7/11.

Using number sense, how would you compare the size of two fractions when their numerators are the same but their denominators are not (e.g., 7/10, 7/8)?

Show/Hide Answer

When two fractions have the same numerator but different denominators such as 7/10 and 7/8, the fraction with the smaller denominator is larger because its partitions are larger (e.g., 1/8 > 1/10). Therefore, 7/8 > 7/10.

Using number sense, how would you compare the size of two fractions when the numerators are 1 partition away from 1 (e.g., 10/11, 6/7) or 2 partitions away from 1 (e.g, 9/11, 5/7) or 3 partitions away from 1 (e.g., 8/11, 4/7)?

Show/Hide Answer

When two fractions have the same number of units away from 1 (e.g., 9/11 and 5/7 where both are 2 partitions away from 1), the one with larger denominator is the larger fraction. Note that 9/11 is 2/11 away from 1 and 5/7 is 2/7 away from 1. Since 2/7 > 2/11 (since 1/7 > 1/11), which means 5/7 is farther away from 1 compared to 9/11; 9/11 is closer to 1. Therefore, 9/11 > 5/7.

Practice Exercises

State the fraction shown in each visualization. Determine if the fraction is proper or improper.

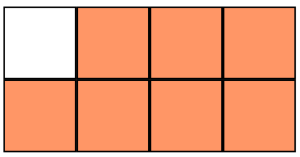2. 3.

Answer the following questions using number sense (i.e., without using a calculator).

Two brands of juice are priced the same per bottle. One bottle holds $\dfrac{7}{8}$ of a pint, while the other holds $\dfrac{5}{6}$ of a pint. Which is the better buy?
In a race, Ben runs 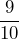$\dfrac{9}{10}$ of a mile in 10 minutes while Seamus runs 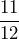$\dfrac{11}{12}$ of a mile in 10 minutes. Who is faster?
When Burger King offered a $\dfrac{1}{3}$ pound burger to compete with McDonalds $\dfrac{1}{4}$ pound burger, their sales dropped since many people thought a $\dfrac{1}{3}$ pound burger smaller than a $\dfrac{1}{4}$ pound burger. Which burger is bigger?

Show/Hide Answer

1. 1. 7/8 Proper fraction
  2. 8/8 Improper fraction
  3. 3/2 Improper fraction
  4. The bottle that holds 7/8 of a pint is the better buy.
  5. Seamus.
  6. Burger King’s 1/3 pound burger.

In this section, we will take what we have learned and apply the concepts to new situations.

Perspectives

You want to make brownies but can only find a ¼ cup measuring cup. The recipe calls for the following items that need to be measured by a measuring cup:

2 cups flour

1 cup sugar

1/8 cup cocoa powder

½ cup milk

a) How many ¼ cups do you need to measure 2 cups of flour?

b) How many ¼ cups do you need to measure 1 cup of sugar?

c) How many ¼ cups do you need to measure 1/8 cup of cocoa powder?

d) How many ¼ cups do you need to measure ½ cup of milk?

2. Ian wants to paint his bedroom. He estimates that it is about half the size of his parents’ living room. His dad painted their living room last year and used 1½ gallons of paint. About how much paint will Ian need to paint his bedroom?

Show/Hide Answer

a) There are four ¼ cups in 1 cup. So there are eight ¼ cups in 2 cups. You need 8 quarter cups of flour.

b) There are four ¼ cups in 1 cup. You need 4 quarter cups of sugar.

c) If ¼ cup is divided into two equal parts, each part will be 1/8 cup. You need 1/2 of a quarter cup of cocoa powder.

d) If 1/2 cup is divided into two equal parts, each part will be ¼ cup. You need 2 quarter cups of milk.

1½ gallons of paint can be represented visually as 1 whole gallon plus 1/2 of a gallon, which is 3/2 of a gallon.

2 paint can. one full, one half full

Ian needs half of this amount so we can take half of each can. Finding half of anything is splitting the amount into 2 equal parts.

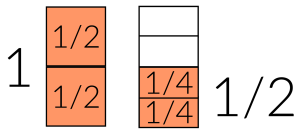
1 whole split into 2 halves. One half split into 2 quarters

Half of 1 is $\dfrac{1}{2}$ and half of $\dfrac{1}{2}$ is $\dfrac{1}{4}$

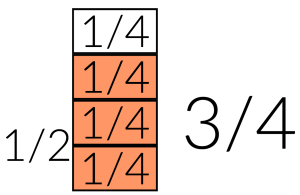
So, Ian needs $\dfrac{1}{2}+\dfrac{1}{4}=\dfrac{2}{4}+\dfrac{1}{4}=\dfrac{3}{4}$ .

Skills Icon In this section, we will use what we have learned so far to practice skill problems.

Skills Practice

In this section use number sense (i.e. no calculator) to answer the questions.

Determine an equivalent fraction with a denominator of 12:

1. $\dfrac{1}{2}$

2. $\dfrac{2}{3}$

3. $\dfrac{1}{6}$

4. $\dfrac{5}{2}$

5. $\dfrac{3}{4}$

6. $\dfrac{7}{4}$

Show/Hide Answer

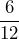
1. $\dfrac{6}{12}$

2. $\dfrac{8}{12}$

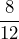
3. $\dfrac{2}{12}$

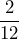
4. $\dfrac{30}{12}$

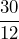
5. $\dfrac{9}{12}$

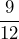
6. $\dfrac{21}{12}$

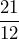
Determine which fraction is larger:

7. $\dfrac{3}{4}$ or $\dfrac{4}{5}$

8. $\dfrac{7}{6}$ or $\dfrac{6}{5}$

9. $\dfrac{2}{3}$ or $\dfrac{5}{3}$

10. $\dfrac{5}{6}$ or $\dfrac{10}{11}$

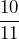
Show/Hide Answer

7. $\dfrac{4}{5}$

8. $\dfrac{7}{6}$

9. $\dfrac{5}{3}$

10. $\dfrac{10}{11}$

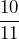
Use number sense and partitioning to answer the questions:

11. What is one-half of $\dfrac{2}{3}$ ?

12. What is one-quarter of $\dfrac{2}{3}$ ?

13. What is three times $\dfrac{1}{8}$ ?

14. What is five times $\dfrac{3}{10}$ ?

15. What is $\dfrac{1}{2}+\dfrac{1}{4}$ ?

16. What is $\dfrac{1}{2}-\dfrac{1}{4}$ ?

17. What is $\dfrac{2}{3}+\dfrac{3}{4}$ ?

18. What is $\dfrac{3}{4}-\dfrac{2}{3}$ ?

19. What is $1+\dfrac{3}{4}$ ?

20. What is $1-\dfrac{3}{4}$ ?

Show/Hide Answer

11. $\dfrac{1}{3}$

12. $\dfrac{1}{6}$

13. $\dfrac{3}{8}$

14. $\dfrac{3}{2}$

15. $\dfrac{3}{4}$

16. $\dfrac{1}{4}$

17. $\dfrac{17}{12}$

18. $\dfrac{1}{12}$

19. $\dfrac{7}{4}$

20. $\dfrac{1}{4}$

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License