CHAPTER 1: NUMBER SENSE

1-4: Number Sense and Relative Size

Number Sense and Relative Size 

Number sense is an essential tool for life. Number sense is the ability to understand, relate, and connect numbers to real life. It is often used for estimating calculations like determining how much wood we’d buy to build a deck, and how much that is going to cost us. Number sense is the ability to compare the sizes of different amounts. For example, $12,345 is a little over one hundred times as large as $123. Number sense is also used to evaluate the feasibility of a numeric calculation. For example, it doesn’t make sense to pay $10,000 per month on a three-year car loan of $25,000.  Evaluating the feasibility of a calculation is even more important to a nurse or doctor when giving the wrong dose of a drug could result in the death of a patient.

Number sense is about making sense of the numbers we use in our lives. Having good number sense will allow us to think about math with an open mind. It will enable us to understand what is being said in the media, in professional papers, in statistics, by our lenders, our retirement account managers, and our kids. It will stop us from being taken advantage of financially, and allow us to quickly check calculations and communicate mathematically.

Explore IconComputational Estimation

Sometimes, we just need to make a quick estimate without getting into the details of a computation to find an exact answer. For example, quickly calculating total cost in a supermarket so that you do not go over the $20 you have left to spend till payday. Estimation that is applied to a computation is called computational estimation. Computational estimation gives us a quick and rough idea about the size of an amount.

There are lots of ways to estimate, but truncation and rounding are two methods that are widely used. The goal of these two methods is to make an estimation as easy and fast as possible.

 

Explore 1 – Truncation

To do a quick and easy estimation, we can simply chop off the decimal portion of numbers so that there are only integers left to work with. This method of chopping off the smaller place values (often the decimal portion) of a number is called truncation.

Ji-Yoo is doing a quick estimation of the total expense for a picnic. The expenses are: $2.35, $5.86, $8.45, $5.44, $9.95.

  1. Truncate the expenses at the decimal point to estimate the total expense.

Solution

To truncate means to cut short. To truncate at the decimal point, we simply cut off any digits after the decimal point. The truncated expenses are: but $2.35\approx\$2, \$5.86\approx\$5, \$8.45\approx\$8, \$5.44\approx\$5, and \$9.95\approx\$9, which totals to $29. We use the symbol \approx to mean ‘approximately equal to’.

  1. Calculate the exact total expense.

Solution

The exact total expense is found by adding up the expenses: $2.35 + $5.86 + $8.45 + $5.44 + $9.95 = $32.05

  1. How far is the estimate away from the exact total expense? Is the estimate an underestimate or an overestimate?

Solution

The estimate is $3.05 less than the exact total expense. \$32.05-\$29=\$3.05. The estimate is an underestimate.

 

Explore 2  – Rounding

Another method for doing a quick and easy estimation is called rounding. We can round to any place value that makes sense in a given situation. To round a number to a certain place value, we look at the digit immediately following the given place value. If that digit is less than 5, we leave the digit in the given place value alone and write the number to that place value. If the digit is greater than or equal to 5, we increase the value of the digit in the certain place value by 1 and write the number to that place value. This is referred to as rounding up.

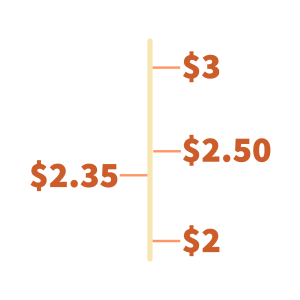For example, we may round $2.35 to the nearest dollar. The digit 2 is in the dollars (ones) place followed by the digit 3. SInce 3 is less than 5, we write the rounded number to $2. Every digit after the rounding place digit will become zero if it lies to the left of the decimal point, and will be dropped off if it lies after the decimal point. In this case, the digits 35 are dropped off. What we are really asking here is, does $2.35 lie closer to $2 or $3? Halfway between $2 and $3 is $2.50. Since $2.35 lies below $2.50, it lies closer to $2.

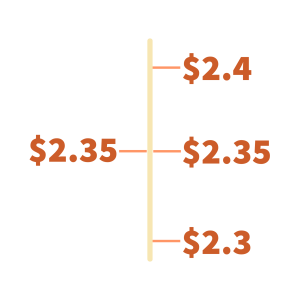To round $2.35 to the nearest ten cents (tenths place), we start with the digit in that place value (3) and consider the digit immediately following it (5). Since 5 is greater than or equal to 5, we round up the tenths place by adding 1 to the digit 3 to get 4. We also dismiss all digits in smaller place values than the tenths place. Therefore, the rounded amount is $2.4. What we are really asking here is, does $2.35 lie closer to $2.3 or $2.4? Halfway between $2.3 and $2.4 is $2.35. Since $2.35 lies at this halfway point, we round up to $2.4.

 

Ji-Yoo is doing a quick estimation for the total expense of a picnic. The expenses are: $2.35, $5.86, $8.45, $5.44, $9.95.

  1. Round the expenses to the nearest dollar to estimate the total expense.

Solution

To round expenses to the nearest dollar, we have to decide which dollar value each expense is closest to. We use the halfway point between each dollar value to determine whether the amount will round up to the next dollar or round down to its current dollar amount. The rounded expenses are: $2 + $6 + $8 + $5 + $10 = $31

  1. Calculate the exact total expense.

Solution

The exact expense is found by adding up the expenses: $2.35 + $5.86 + $8.45 + $5.44 + $9.95 = $32.05

  1. How far is the estimate away from the exact total expense?

Solution

The estimate is $1.05 less than the exact total expense. \$32.05-\$31=\$1.05

  1. Considering the estimate in Explore 1, which estimate is closer to the total expense?

Solutions

The closest estimate is $31 which was found by rounding then adding.

 

Examples

  1. It has been estimated that fleas can jump 150 times their own body height. If humans could do the same thing, estimate how high a 6 feet 4 inch human could jump?
Show/Hide Answer

The only number that needs to be simplified for estimation purposes is 6 feet 4 inches. We can round that to 6 feet. Therefore, the estimate is 150\times6 feet =900 feet.

However, we could also round 150 to 200 and get the estimate 200\times6 feet = 1200 feet. It all depends on how rough of an estimate you need for your answer. The estimate of 900 feet underestimates the actual answer of 950 feet, while the estimate of 1200 feet overestimates the actual answer.

  1. Brian is trying to estimate how much it will cost to rent a car for 21 days if it costs $45.36 per day, including taxes. Estimate his cost, then determine how far off the estimate is from the actual cost.
Show/Hide Answer

We can round all numbers to the nearest ten: 21 days \approx 20 days; $45.36 \approx $50.

Therefore, the estimated cost is \$50\times20=\$1000.

The actual cost is \$45.36\times21=\$952.56 The estimate is $47.44 higher than the actual cost. This is an overestimate.

 

Reflect Icon

  • Why do we round or truncate numbers when estimating?
Show/Hide Answer

To have easier numbers to deal with especially if we are multiplying or dividing.

  • What is the difference between truncating and rounding?
Show/Hide Answer

With truncation, the numbers past a decided value place are simply chopped off. With rounding, we look at the digit immediately following the decided place value and round up or down depending on whether that digit is greater than or equal to 5 or less than 5, respectively.

  • What is the benefit of estimation?
Show/Hide Answer

It gives a quick and easy answer to a calculation. It allows us to spot errors in a calculation.

  • Is it better to overestimate or underestimate? Explain your reasoning.
Show/Hide Answer

It depends on the circumstances. It may be better to overestimate the cost of buying something so that we know we’d have enough money, but it may be better to underestimate the weight capacity of a tow rope so that it does not break while towing.

 

Explore IconEstimation for Plausibility

Having good number sense includes the ability to determine if a given answer is plausible or not. Knowing when a given number, amount or statistic is valid or reasonable is a vital life skill. We can combine common sense with computation estimation to help us determine whether a given or computed amount is reasonable or not.

Explore 3  – Truncation

Jane is buying a car that costs $30,450. The finance manager says she will pay $5193 monthly for a three-year car loan. Using just number sense or your estimation skills, determine if the monthly payment amount makes sense. Explain your reasoning.

Solution

  • Just using common sense a $5193 monthly payment is more than most people earn in a month. Also, if you have any experience with car loans you will realize that most loan payments are around $200 to $800 per month, so $5193 seems incredibly high. Indeed, $5193 per month is much higher than most mortgage payments, so a car payment of $5193 makes no sense.
  • We could do a quick calculation to approximate how long it would take to pay off the $30,000 loan, paying $5000 per month. If we truncate the numbers at the thousands place, $30,450 truncates to $30,000 and $5193 truncates to $5000.  Since $30,000 ÷ $5000 = 6, only six monthly payments of $5000 will pay off the loan. Consequently, three years with 36 monthly payments is not reasonable.
  • Alternatively, the cost of the car is approximately $30k (k stands for thousand). The monthly payment is approximately $5k. Since $30k is 6 times the value $5k, six monthly payments will pay off the loan. Consequently, three years with 36 monthly payments is not reasonable.

 

Explore 4  – Rounding

Suppose that your car can travel about 384 miles on a full tank of gas. You are driving 131.6 miles from Reno to Sacramento to meet with a possible investor for your start-up business. As you turn on your car, you notice that you have half of a tank of gas. Can you make it to Sacramento without filling up the tank?  Can you make it back again to Reno without filling up? Using the rounding method to do a quick estimation that answers the questions. Explain your reasoning.

Solution

Rounding to the nearest hundred 384 miles is approximately 400 miles. Since the tank is half full, half of 400 miles is 200 miles (400 ÷ 2 = 200). Since 200 miles are more than 131.6 miles, you can make it to Sacramento without filling up the tank. 

Making it back to Reno is another matter. 131.6 miles is approximately 130 miles (rounding to the nearest ten). So the distance from Reno to Sacramento then back to Reno is approximately 2\times130 miles =260 miles. This is higher than the approximately 200 miles you can travel on a half tank of gas, so you will not make it back to Reno without filling up.

 

Examples

1. Utah’s state sales tax rate for 2023 is 4.85 percent [1] which is equal to 0.0485. Ming states that the smallest monetary unit is a cent. The tax rate does not make any sense because the tax rate apparently has smaller units than “cent”.  Do you agree with Ming’s reasoning? Explain your answer.

Show/Hide Answer

Tax rates do not have to stop at the hundredths place like cents. When the tax rate is multiplied by a dollar amount to find the tax due (e.g., 0.0485\times$500=\$24.25) it may turn out to be an exact dollar and cents amount. Even if it doesn’t (e.g., 0.0485\times$50=\$2.425), the tax due will be rounded to the nearest cent.

 

2. A school decides to lower it’s class size from 30 to 25 students. The principal’s report to the district states that the lower class sizes will result in an increase from 8 to 10 classes over 5 grades, and that two new teachers will need to be hired. Does the principal’s report make sense?

Show/Hide Answer

If each of the 8 classes is reduced by 5 students, there will be 40 students that need to be reclassed. So at first glance, 2 new classes sounds fine. However, although 40 students can be put into 2 classes of 25 students or less, these new classes could consist of students from 5 different grades. Consequently, the principal’s report does not make sense.

 

3. In a 2020 news interview, a tweet made by writer Mekita Rivas was discussed.

“Bloomberg spent $500 million on ads. The U.S. population is 327 million. He could have given each American $1 million and still have money left over. I feel like a $1 million check would be life-changing for most people. Yet he wasted it all on ads and STILL LOST.”

Does the statement in the tweet sound plausible? Explain your answer.

Show/Hide Answer

No, it is not plausible. 327 million people is approximately 3\times10^8 people, and $1 million =\$10^6. If each of the 300 million people were given $1 million, the total would be 3\times10^8\times\$10^6=\$3\times10^{14}. This far exceeds the $500 million spent by Bloomberg.

 

 

  • Reflect IconWhat is plausibility for a given amount?
Show/Hide Answer

Plausibility is how valid or reasonable a given amount is.

  • How does estimation help determining plausibility in real life?
Show/Hide Answer

Estimation can give us a rough estimate of what an answer should be so it tells us if the answer is in the right ball park.

  • Can we always trust estimation for determining plausibility in our daily life?
Show/Hide Answer

It depends. If we are looking for a close estimate, we might not be satisfied because an estimate may not be close enough. If we are looking for a rough estimate, we may be satisfied. We also have to use common sense.

 

Investigation IconPlausibility of a Statement

Forrest Gump ran for “3 years, 2 months, 14 days and 16 hours.” It was quoted that he ran all the way across the United States four times.

  1. Is it possible to run across the US from coast to coast? Explain your answer.
  2. How long would it take an average person to run from coast to coast?
  3. How plausible is the quote regarding Forrest Gump? Explain your reasoning.

 

Explore IconAbsolute and Relative Measures

Size can be absolute or relative. Absolute size is the actual measurement of the object. For example, the Empire State Building is 1454 feet tall. But from an airplane, the Empire State Building could seem ridiculously small. This is the size of the Empire State Building relative to the observer. Relative size can also be used when we are comparing the size of two things: the size of one thing relative to the size of another thing. For example, we could say, “I bought a watermelon that was bigger than my head.” This simile gives us a visual representation of the size of the watermelon.

One way of determining the relative size between two amounts is to divide one amount by the other. This division will determine how many times one is amount is of the other amount.

Explore 5  – Relative size using division

The world’s tallest building is the Burj Khalifa in Dubai at 828 meters. A five-story building is about 17 meters high. How many times as tall is the Burj Khalifa to a typical five-story building?

Solution

To determine how many times as tall is the Burj Khalifa to a typical five-story building, we divide the height of the Burj Khalifa by the height of a five-story building: 828\div17\approx 49. The Burj Khalifa is about 49 times as tall as a typical five-story building.

 

Explore 6 – Relative size using estimation

Utah Valley University sits at an elevation of about 1402 meters. [2] The elevation of nearby Timpanogos Peak is 3582 meters.[3]

  1. The elevation of Timpanogos Peak is roughly how many times the elevation of Utah Valley University?
  2. The average height of a story in a multi-story building is about 4 meters. If a building at UVU reached the elevation of Timpanogos Peak, estimate the number of stories it would have.

Solutions

  1. Rounding to the nearest thousand meters, the elevation of Utah Valley University is about 1000 meters, and the elevation of Timpanogos Peak is about 4000 meters. Timpanogos Peak is about 4 times the elevation of Utah Valley University (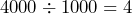4000\div1000=4. This is a very rough estimate. To get a closer estimate we can round the elevations to the nearest 100 meters: Utah Valley University 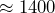\approx 1400 meters and Timpanogos Peak 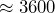\approx 3600 meters. Then 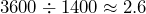3600 \div 1400\approx2.6 tells us that the elevation of Timpanogos Peak is about 2.6 times the elevation of Utah Valley University.
  2. The difference in elevation is about 3600 meters – 1400 meters = 2200 meters. So from ground level at UVU the building would have to be 2200 meters tall. Since each story is approximately 4 meters, the building would have 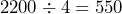2200\div4=550 stories.

 

Explore 7 – Relative size

The population of the Salt Lake City metro area at the end of 2022 was about 1.258\times10^6. As of January 2023, the population of the United States was about 3.36\times10^8. Estimate how many times the population of the U.S. is to the population of the Salt Lake City metro area.

Solution

Using truncation to estimate: You may truncate the decimal part of the number portion of the scientific notation. 1.258 truncates to 1, while 3.36 truncates to 3. The difference between the exponents will be the relative size difference in terms of the multiple of 10. So, (3\times10^8)\div(1\times10^6)=(3\div1)\times(10^8\div10^6)=3\times10^2=300. The population of the U.S. is about 300 times the population of the Salt Lake City metro area.

Using rounding to estimate: Rounding the decimal part of the numbers in scientific notation to the ones place gives the same estimate as truncation. If we instead round to the tenths place we get 1.258 rounding to 1.3, and 3.36 rounding to 3.4. The difference between the exponents will be the relative size difference in terms of the multiple of 10. Then (3.4\div1.3)\times10^2=2.62\times100=262. The population of the U.S. is about 262 times the population of the Salt Lake City metro area.

 

  • Reflect IconWhat is the relative size between two amounts?
Show/Hide Answer

Relative size tells us how much larger or smaller an amount is compared to the other amount. It is found by dividing one amount by the other amount.

  • How does estimation help determine the relative size between two amounts?
Show/Hide Answer

Estimation gives us an approximate answer using quick and easy arithmetic.

  • What are the benefits of using estimation in determining the relative size between two amounts?
Show/Hide Answer

We usually don’t need to know the exact size factor of one amount to another. Usually an estimate will do, and an estimate can be done quickly and easily without the need for a calculator.

  • Give an example of relative size being used in life.
Show/Hide Answer

A painter uses their thumb to determine the relative size of the facial features of a portrait they are painting.

 

Practice Exercises

    1. Estimate the cost of filling up a 16.2 gallon tank with gas that costs $3.54 per gallon. Compare your estimate with the actual cost.
    2. Estimate the time to print a paper that is 23 pages long if the printer you are using prints 8 pages per minute. Compare your estimate with the actual time.
    3. Estimate a 20% tip on a restaurant bill of $76.30.
    4. In 2020, the average American family credit card debt was $6270, totaling $607 billion. Estimate how many average American families carry credit card debt.
    5. The wingspan of a B-2 Stealth Bomber is about 30 times the width of a Honda Civic. If a Honda Civic is about 5 feet wide, what is the approximate wingspan of a B-2 Stealth Bomber? 
    6. The amount of water surface area on the Earth is about 140 million square miles. The total surface area of the Earth is about 197 million square miles. Estimate many times the total surface area of the Earth is compared to the water surface area of the Earth?
    7. Billy is buying tickets for his family to go to the movies. The tickets cost $12.59 for adults and $5.49 for children under 16. He needs to buy two adult tickets and three children’s tickets. Estimate the cost of the tickets using a) truncation, and b) rounding. Which method gives an estimation that is closer to the actual value?
    8. A social media post claims: “20 minutes of exercise every day equals over 1000 hours of exercise a year.” Determine if this post is plausible.
    9. Utah is an alcoholic beverage control state where the sale of liquor and spirits is state-controlled. The Utah liquor excise tax rate is 4.85 cents per dollar spent.  a) Estimate the excise tax paid to the state on a $75 bottle of Scotch.  b) Calculate the exact excise tax paid to the state on a $75 bottle of Scotch. c) Wyoming has no excise tax. Would it be worthwhile to drive to Wyoming to save money? Explain your reasoning.
Show/Hide Answer

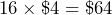    1. Estimated cost = 16\times\$4=\$64 or estimated cost =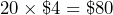 20\times\$4=\$80

      Actual cost = 16.2\times\$3.54=\$57.348\approx\$57.35

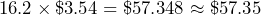
    2. Estimated time = 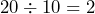20\div 10=2minutes

      or

      Estimated time = 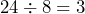24\div8=3 minutes

      Actual time = 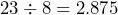23\div8=2.875 minutes

      The estimate of 2 minutes is an underestimate, while the estimate of 3 minutes is an overestimate.

    3. One way to estimate a tip is to round the bill: $76.30 \approx $80.

      Then divide by 10 and multiply 2: Tip = \$80\div10\times2=\$16

      This gives an approximately 20 percent tip.

    4. If we round to the highest place value of each number and write the numbers in scientific notation, we get 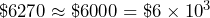\$6270\approx\$6000=\$6\times10^3 and $607 billion 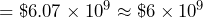=\$6.07\times10^9\approx\$6\times10^9. Then 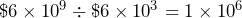\$6\times10^9\div\$6\times10^3=1\times10^6. So, approximately 1 million average American families carry credit card debt.

    5. 150 feet
    6. The total surface area of the Earth is about twice the water surface area of the Earth.
    7. a) $39 (truncating at the decimal point); b) $41 (rounding to the nearest dollar); The actual cost is $41.65. The rounding method of estimation is closer.
    8. 20 minutes every day amounts to 60 minutes = 1 hour every 3 days. Since it takes 3 days to complete 1 hour of exercise, it will take 1000 times 3 days = 3000 days to complete 1000 hours of exercise. 1 year is 365 days and 3000 days is almost ten times that. So no, the post is not plausible.
    9. a) Estimate = (5 cents per dollar)($80) = 400 cents = $4 b) $3.6375, which rounds to $3.64 c) No. It would cost way more than $3.64 in gas to drive to Wyoming and back.

 

Detour IconAbsolute and Relative Speed

Speed can be an absolute or relative measure. To a person standing still, a car that is traveling at 25 miles per hour will appear to be traveling at 25 miles per hour. But if that car overtakes a cyclist traveling at 10 miles per hour in the same direction as the car, that car is moving 15 miles per hour faster than the cyclist. So, relative to the cyclist, that car is moving at 15 miles per hour.

Velocity is speed with direction. When objects are moving in opposite directions, one will have a positive velocity and the other will have a negative velocity. A train traveling north may have a velocity of 60 miles per hour. A train traveling south, in the exact opposite direction, that is traveling at a speed of 50 miles per hour will have a velocity of -50 miles per hour. This means that relative to each other, the trains pass at 60-(-50)=110 miles per hour.

  • What is the relative speed of two cars traveling in the same direction if one car is traveling at 65 mph and the other car passes it at 70 mph?
Show/Hide Answer

5 mph

  • What is the relative speed of two cars traveling in opposite directions on a freeway, if one car is traveling at 70 mph and the other car is traveling at 80 mph?
Show/Hide Answer

150 mph

  • What is the relative speed of an express train passing through a station at 80 mph to an observer standing still?
Show/Hide Answer

80 mph

  • What is the relative speed of two high speed trains passing one another in opposite directions if they are both traveling at 120 mph?
Show/Hide Answer

240 mph

  • What is the relative speed of a car hitting a brick wall at 30 mph?
Show/Hide Answer

30mph

  • What is the relative speed of a head-on collision if one car is traveling at 40 mph and the other at 55 mph? Why are head-on collisions of two moving vehicles so destructive?
Show/Hide Answer

95 mph

 

In this section, we will take what we have learned and apply the concepts to new situations.

Perspectives

  1. As of 2023, the tallest dog on record was a Great Dane named Zeus who measured 111.8 centimeters from the ground to his withers. In contrast, the smallest dog on record was a fist-sized, dwarf Yorkshire terrier who stood 7.11cm.  a) Estimate how many times taller Zeus was to the Yorkshire terrier.     b) How close is your answer to the exact answer?     c) Was Zeus taller than you? Explain your reasoning.     d) Was the Yorkshire terrier taller than a can of Coke? Explain your reasoning.
  2. The age of the Earth is estimated to be 4,600,000,000 years old. Current evidence [4] supports modern Homo sapiens appearing around 190,000 B.C.E. How many times longer has Earth been around than the Homo sapiens?
  3. Combined sales tax in Utah County in 2023 is 7.25 cents for each dollar spent. If Matt buys a new couch for $2269, roughly how much should he expect to spend on taxes?
  4. The 5.15 meter tall statue of David was created by Michelangelo between 1501 and 1504. It was carved out of a single block of marble. The average height of an Italian man is 1.765 meters. a) Estimate how many times taller the statue of David is to an average Italian man.  b) Estimate how many times smaller you are to the statue of David.
  5. African savanna elephants are the largest animals walking the Earth. Their herds wander through 37 countries in Africa. They can reach 13 feet in height to their shoulder and weigh up to 7 tons.  African forest elephants are the elusive cousin of the African savanna elephant. They inhabit the dense rainforests of west and central Africa. They are critically endangered due to poaching and loss of habitat. African forest elephants can reach 10 feet and 5 tons. a) How many times taller is the African savanna elephant than the African forest elephant?     b) How many times heavier is the African savanna elephant than the African forest elephant?
Show/Hide Answer
  1. a) 111.8 centimeters rounds to 100 centimeters. 9.65 centimeters rounds to 10 centimeters. So, Zeus was 10 times the size of Miracle Milly.     b) Exact answer is 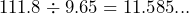111.8\div9.65=11.585... times the size.     c) 111.8 centimeters is less than 4 feet, so no.     d) A can of Coke is 12.27 centimeters high.[5] So, since 7.11 cm is shorter than 12.27 cm, the Yorkshire Terrier was not taller than a can of Coke..
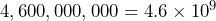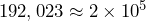  2. 190,000 B.C.E. is equivalent to -190,000 C.E., so Homo sapiens have been on Earth 2023-(-190,000) = 192,023 years.4,600,000,000 = 4.6\times10^9 and 192,023\approx2\times10^5Therefore, 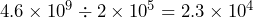4.6\times10^9\div2\times10^5=2.3\times10^4.Earth has been around about 23,000 times longer than Homo sapiens.
  3. 7.25 cents rounds to 7 cents. $2269 rounds to $2000. SO Matt can expect to spend 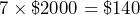7\times\$2000=\$140 in sales tax.
  4. a) 5.15 meter is approximately 5 meters; 1.765 meters is approximately 2 meters. So David is approximately 2.5 times as tall as an average Italian man.     b) If you are 1.7 meters tall, you are approximately 2.5 times as small as the statue of David.
  5. a) 13 feet compared to 10 feet: 1.3 times taller.    b) 7 tons compared to 5 tons: 1.4 times heavier.

 

 

Skills IconIn this section, we will use what we have learned so far to practice skill problems.

Skills Exercises

Perform the following operations using a scientific calculator. Write the answer in scientific notation.

  1. (2.1\times10^2)(3.4 \times10^{-5})
  2. (8.4\times10^{-3})\div(2.1\times10^7)
  3. (3.2\times10^{14})(1.03\times10^{-22})
  4. \dfrac{1.4\times10^{-8}}{2.5\times10^6}
Show/Hide Answer
  1. 7.14\times10^{-3}
  2. 4\times10^{10}
  3. 3.296\times10^{-8}
  4. 3.5\times10^{-2}

 

Truncate the numbers at the decimal point:

  1. 0.999
  2. 0.237
  3. 23.879
  4. 23.005
Show/Hide Answer
  1. 0
  2. 0
  3. 23
  4. 23

Round the numbers to the given place value:

  1. 2,386,975 to the nearest hundred-thousand
  2. 876.349 to the nearest tenth
  3. 0.08708 to the nearest one
  4. 0.798209 to the nearest hundredth
Show/Hide Answer
  1. 2,400,000
  2. 876.3
  3. 0
  4. 0.80

 

  1. https://www.avalara.com/taxrates/en/state-rates/utah/cities/salt-lake-city.html ↵
  2. https://elevation.maplogs.com/poi/utah_valley_university_w_university_pkwy_orem_ut_usa.382774.html ↵
  3. https://www.peakbagger.com/peak.aspx?pid=5474 ↵
  4. https://www.prb.org/articles/how-many-people-have-ever-lived-on-earth/ ↵
  5. https://www.measuringknowhow.com/coke-can-dimensions/ ↵
definition

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

Numeracy Copyright © 2023 by Utah Valley University is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.