CHAPTER 1: NUMBER SENSE
1-3: Scientific Notation
Scientific notation is an efficient, shorthand way of expressing very large or very small numbers. Scientific notation gives us an instant idea of how large or small a number is without having to count all those zeros to determine place value. Scientific notation gets its name because it is primarily used in the sciences, but it can be used in any field.
 Scientific Notation with Positive Exponents
Scientific Notation with Positive Exponents
Scientific notation is composed of a product of two parts; a decimal number part and a power of 10 part. For example, ![]() . The number part must be a decimal that is greater than or equal to 1 but less than 10. Any number may be expressed in scientific notation. Scientific notation gives us an instant idea of how large or small a number is without having to count all those zeros to determine place value. For example,
. The number part must be a decimal that is greater than or equal to 1 but less than 10. Any number may be expressed in scientific notation. Scientific notation gives us an instant idea of how large or small a number is without having to count all those zeros to determine place value. For example, ![]() immediately tells us that we are dealing with a number in the thousands since the exponent is 3.
immediately tells us that we are dealing with a number in the thousands since the exponent is 3.
Explore 1 – Number sense using scientific notation
The distance from New York to San Francisco is about ![]() miles. The circumference of the earth is about
miles. The circumference of the earth is about ![]() miles. The difference of the two exponents is 4 – 3 = 1, which tells us that the circumference of the earth is about ten times (i.e.,
miles. The difference of the two exponents is 4 – 3 = 1, which tells us that the circumference of the earth is about ten times (i.e., ![]() ) the distance from New York to San Francisco. Alternatively, the difference of the exponents is 3 – 4 = -1, which tells us that the distance from New York to San Francisco is about one-tenth the circumference of the earth since
) the distance from New York to San Francisco. Alternatively, the difference of the exponents is 3 – 4 = -1, which tells us that the distance from New York to San Francisco is about one-tenth the circumference of the earth since ![]() .
.
The distance between Earth and the moon is about ![]() miles. Use the difference between the exponents to determine how many times as long the distance between Earth and the moon is to the distance from New York to San Francisco.
miles. Use the difference between the exponents to determine how many times as long the distance between Earth and the moon is to the distance from New York to San Francisco.
Solution
The difference in exponents is 5 – 3 = 2, so the distance between Earth and the moon is about 100 times the distance from New York To San Francisco.
 Entering Scientific Notation in a Calculator
Entering Scientific Notation in a Calculator
As always, entering scientific notation into a calculator is dependent on the calculator you are using, but there are typically two options; the ![]() button or the
button or the ![]() button.
button.
Many scientific calculators have a button with the letters EE imprinted on it. This button means Enter Exponent and allows us to enter a power of 10. For example, to input the number ![]() we type in:
we type in:
![]()
The display will have the decimal 3.45 followed by the power 7 displayed as ![]() or something similar.
or something similar.
If we press ![]() after inputting the expression, the calculator will show
after inputting the expression, the calculator will show ![]() . The calculator converts the scientific number to a decimal number if there are enough spaces in the display to show all the digits. If not, the scientific number will remain.
. The calculator converts the scientific number to a decimal number if there are enough spaces in the display to show all the digits. If not, the scientific number will remain.
The ![]() button works in a similar way. The
button works in a similar way. The ![]() or
or ![]() buttons raise 10 to the power that is in the display of the calculator. So, to raise 10 to the power of 7, the input is
buttons raise 10 to the power that is in the display of the calculator. So, to raise 10 to the power of 7, the input is ![]() .
.
To input the number ![]() , the input is
, the input is ![]()
![]() and displays
and displays ![]() or the decimal
or the decimal ![]() .
.
Calculations done using scientific notation may display as scientific notations or as decimals.
Explore 2 – Writing decimal numbers in scientific notation using place value
We write a decimal number using place values. For scientific notation, we write a number based on the place value of its first non-zero digit. For example, the number 9560 has the digit 9 in the thousands place. We may write 9560 as 9.560 thousands, or, since ![]() , we write
, we write ![]() .
.
Walmart’s net income was about 13.7 billion dollars in 2022[1], which is $13,700,000,000. The place value of the digit 1 is the ten-billions place. We may write the number as 1.37 ten-billions, or, since ten-billions ![]() , we write
, we write ![]() .
.
Write the following numbers in scientific notation.
- The average home value in Los Angeles in 2022 was about $951,000[2].
Solution
The 9 in $951,000 is in the hundred thousands place, which is ![]() . So,
. So, ![]() in scientific notation.
in scientific notation.
- The population of the Salt Lake City metro area at the end of 2022 was about 1,258,000 people[3].
Solution
1,258,000 people is 1.258 million people. Million ![]() , so
, so ![]() people
people ![]() people.
people.
Explore 3 – Writing numbers in scientific notation by moving the decimal point
Instead of using the place value of the first non-zero digit in the number to determine the power of 10 in scientific notation, we can count the number of places and direction we must move the decimal point to get from a number between 1 and 10 for the decimal part back to the original number. For example, to write scientific notation for the number 9561, we put the decimal point after the first non-zero digit (9) and use 9.561 as the decimal part. To get back to 9651 from 9.560, we need to move the decimal point of the number 9.561 three places to the right, which is equivalent to multiplying by 1000 or 103. Therefore, the number 9561 is written as ![]() in scientific notation.
in scientific notation.
Write the following numbers in scientific notation.
- As of January 2023, the population of the United States is about 336,000,000 people.
Solution
The decimal part is 3.36 (we don’t write all the zeros!) and the decimal point would need to be moved 8 places to the right to get back to 336,000,000. Therefore, 8 is the power on the 10. In scientific notation, 336,000,000 people is written as ![]() people.
people.
- The population of the world in 2023 is around 8 billion people.
Solution
8 billion as a decimal is 8,000,000,000. The decimal part is 8, whose (unwritten) decimal point would need to be moved 9 places to the right to get back to 8,000,000,000. Therefore 8 billion people is written in scientific notation as ![]() people.
people.
- The distance from Earth to Mars is about 33.9 million miles.
Solution
33.9 million as a decimal is 33,900,000. Therefore, the decimal part of scientific notation is 3.39 and the decimal point would need to be moved 7 places to the right to get back to 33,900,000. In scientific notation, 33.9 million miles ![]() miles.
miles.

- Why is scientific notation important?
Show/Hide Answer
It allows very large numbers to be written in a concise form. It gives immediate information on how large a number is from the power of 10. It gives a quick answer to a comparison of size.
- How can we use scientific notation to get a quick estimate of how much larger or smaller one number is to another? Give an example.
Show/Hide Answer
Subtract the exponents on the powers of 10 in the scientific notation. For example if object 1 has a height of ![]() centimeters and object 2 has a height of
centimeters and object 2 has a height of ![]() centimeters, then the difference in exponents is 5 – 2 = 3. Therefore, object 2 is about 103 or 1000 times taller than object 1.
centimeters, then the difference in exponents is 5 – 2 = 3. Therefore, object 2 is about 103 or 1000 times taller than object 1.
- What is the relationship between the place value of the first non-zero digit in a decimal number and the power of 10 in scientific notation? Give an example.
Show/Hide Answer
The place value of the first non-zero digit corresponds to the power of 10 used in scientific notation. For example, in the number 456,000, the 4 is in the hundred-thousands place. One hundred-thousand = 105 so the power of 10 in scientific notation is also 105. In scientific notation, 456,000 ![]() .
.
- What does the exponent in scientific notation tell us about the decimal number? Give an example.
Show/Hide Answer
It tells us the place value of the first non-zero digit in the decimal number. For example, the exponent of 6 in ![]() tells us that the 3 is in the 6th place before the decimal point (i.e., the millions place).
tells us that the 3 is in the 6th place before the decimal point (i.e., the millions place).
- How is the decimal point and exponent in scientific notation related to a number? Give an example.
Show/Hide Answer
The number of places the decimal point has to move from the decimal part of scientific notation to get back to the original number tells us the exponent on the 10 in scientific notation. For example, the exponent 4 in ![]() tells us that we need to move the decimal point in 1.8 four places to the right to get the number 18,000.
tells us that we need to move the decimal point in 1.8 four places to the right to get the number 18,000.
 Scientific Notation with Negative Exponents
Scientific Notation with Negative Exponents
Explore 4 – Writing numbers in scientific notation using place value
In Explore 2, we saw that the scientific notation of a number may be derived by using the place value of the first non-zero digit of the number. Let’s explore if this method works for a decimal number that is smaller than one (i.e., a fractional decimal).
Write the following numbers in scientific notation.
- A single red blood cell is about 0.0000078 meters in diameter.[4]
Solution
For the number 0.0000078, the first non-zero digit (7) is in the place value millionths (![]() ). Therefore, in scientific notation
). Therefore, in scientific notation ![]() meters
meters ![]() .
.
- The length of a Queen Fire Ant is about 0.006 meter.[5]

Solution
The first non-zero digit (4) is in the thousandth place. One-thousandth ![]() , so
, so ![]() meters
meters ![]() meters.
meters.
- The size of the smallest mite is about 0.0001 meter.[6]
Solution
The first non-zero digit is in the ten-thousandth place. One ten-thousandth ![]() , so in scientific notation
, so in scientific notation ![]() meters
meters ![]() meters.
meters.
Explore 5 – Writing numbers in scientific notation by moving the decimal point
In Explore 3, we saw that the scientific notation of a number may be derived by counting the number of places we have to move the decimal point to get from the decimal part back to the original number. For example, for the number 0.000007, we need to move the (unwritten) decimal point of the number 7 to the left 6 places to turn 7 into 0.000007. This is equivalent to dividing 7 by ![]() or multiplying 7 by
or multiplying 7 by ![]() (see section 1-2). Therefore, the number 0.000007 may be written as
(see section 1-2). Therefore, the number 0.000007 may be written as ![]() .
.
Write the following numbers in scientific notation.
- A bacteria is about one millionth of a meter in diameter.
Solution
One millionth ![]() . From the first non-zero digit (1), we have to move the decimal point 6 places to the left. One millionth of a meter is
. From the first non-zero digit (1), we have to move the decimal point 6 places to the left. One millionth of a meter is ![]() meters.
meters.
- A hydrogen atom is about 0.0000000000529 meters.[7]
Solution
To turn 5 into 0.0000000000529, we have to move the decimal point 11 places to the left. So, ![]() meters
meters ![]() meters.
meters.

- How do you turn a number written in scientific notation to a decimal number?
Show/Hide Answer
Write the decimal part of the number and move the decimal point the exponent on the 10 number of places to the right if the power is positive and to the left if the power is negative.
Examples
- Uwe reaches his goal of 10,000 steps daily. Write this number in scientific notation.
- The amount of water surface area on the Earth is about 140 million square miles. Write this number in scientific notation.
Show/Hide Answer
- There are 4 zeros after the 1 in 10,000, so the exponent on the 10 in scientific notation must be 4. So, 10,000 steps
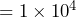 steps.
steps. - 140 million square miles = 140,000,000 square miles. For scientific notation the decimal part is 1.4 and the decimal point has to move 8 places to the right to get back to 140,000,000. This means the power on the 10 is 8. So, 140 million square miles
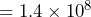 square miles.
square miles.
 Viruses
Viruses
Viruses are a common cause of illness, yet a typical human virus ranges in size from only about ![]() meters to about
meters to about ![]() meters in diameter.[8]
meters in diameter.[8]
- Express these numbers as decimals.
- What is the size of the Covid-19 virus?
- What type of mask is required to filter out Covid-19?
Practice Exercises
- Amazon’s net income in 2021 is 33.36 billion dollars[9].
- As of January 27, 2023, the US National Debt is about $31.5 x 1013 (Note that this is not written in scientific notation because the number part, 31.5, should be between 1 and 10).
- The age of the Earth is estimated to be 4,543,000,000 years old[10]. Express the age of the Earth in scientific notation.
- Homo-sapiens have lived on Earth for around 300,000 years.[11] Express the age of homo-sapiens in scientific notation.
- Use your answers from questions 3 and 4 to approximate how many times longer Earth has been around than homo-sapiens.
- A hydrogen atom is about
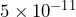 meters across, which is about 2 million times smaller than the width of a human hair. Write
meters across, which is about 2 million times smaller than the width of a human hair. Write 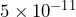 meters as a decimal.
meters as a decimal. - The painting Shot Sage Blue Marilyn, 1964 by Andy Warhol sold for $195 million in 2022[12], making it the most expensive work of art created in the 20th century. Write $195 million in scientific notation.
 The smallest flower on Earth is Watermeal[13] which averages 0.024 inches by 0.012 inches. Write these measurements in scientific notation.
The smallest flower on Earth is Watermeal[13] which averages 0.024 inches by 0.012 inches. Write these measurements in scientific notation.
Show/Hide Answer
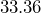 billion
billion 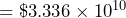
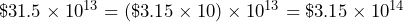
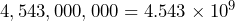 years old
years old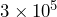 years old.
years old.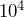 or 10,000 times longer.
or 10,000 times longer.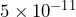 meters = 0.00000000005 meters
meters = 0.00000000005 meters- $195 million
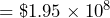
- 0.024 inches
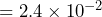 inches and 0.012 inches
inches and 0.012 inches 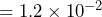 inches.
inches.
 In this section, we will take what we have learned and apply the concepts to new situations.
In this section, we will take what we have learned and apply the concepts to new situations.
Perspectives
- China has a population of about 1.4 billion people.[14] The world has a population of about 8 billion people. a) Write the population of China in scientific notation. b)Write the world population in scientific notation.
- Pollen grains cause allergies in many people, but they are usually too small to see with the naked eye. A grain of ragweed pollen, for example, is only about 0.00002 meters in diameter.[15] How is this number written in scientific notation?
- To write the entire diploid human genome it takes up
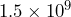 bytes or 1.5 Gigabytes of space on a hard drive, about 2 CDs worth![16] Write
bytes or 1.5 Gigabytes of space on a hard drive, about 2 CDs worth![16] Write 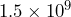 bytes as a decimal number.
bytes as a decimal number. - The number of cells in the human body is estimated at
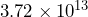 [17]. Write this number as a decimal.
[17]. Write this number as a decimal. - The U.S. has a population of about 330.2 million people[18]. The world has a population of about 8.0 billion people [19]a) Write the U.S. population in scientific notation. b) Write the world population in scientific notation. c) How many times is the world population as big as the U.S. population?
- The approximate mass of the average human cell is 0.000000000001 kilograms [20]. Write this number in scientific notation.
Show/Hide Answer
- a) Since billion
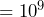 , 1.4 billion people is
, 1.4 billion people is 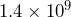 people. b) Since billion
people. b) Since billion 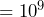 , 8 billion people is
, 8 billion people is 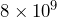 people.
people. - If we put the decimal point after the 2, we need to move the decimal point 5 places to the left to get back to 0.00002. Therefore the power on the 10 in scientific notation is -5. 0.00002 meters
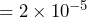 meters.
meters. - Since the power on 10 is 9, we have to move the decimal point in 1.5 nine places to the right:
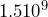 bytes = 1,500,000,000 bytes.
bytes = 1,500,000,000 bytes. - Move the decimal point 13 places to the right: 150,000,000,00,000.
- a)
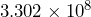 people. b)
people. b) 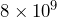 people. c) World population is about 24 times the U.S. population.
people. c) World population is about 24 times the U.S. population. 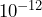 kilograms
kilograms
 In this section, we will use what we have learned so far to practice skill problems.
In this section, we will use what we have learned so far to practice skill problems.
Skill Exercises
Convert the following decimal numbers into scientific notation.
Show/Hide Answer
Convert the following scientific numbers into decimals.
Show/Hide Answer
- Walmart net income ↵
- Average home values in Las Angeles. ↵
- Population of Salt Lake City ↵
- Size of a blood cell. ↵
- Length of a fire ant ↵
- Size of a mite. ↵
- Empty space in an atom ↵
- Size of a virus. ↵
- Amazon's net income. ↵
- Age of the Earth. ↵
- Mans time on Earth ↵
- Value of Sage Blue Marilyn ↵
- Watermeal ↵
- Population of China ↵
- Karger article on pollen. ↵
- How much information is in the human genome? ↵
- Bianconi, Eva; Piovesan, Allison; Facchin, Federica; Beraudi, Alina; Casadei, Raffaella; Frabetti, Flavia; Vitale, Lorenza; Pelleri, Maria Chiara; Tassani, Simone (Nov–Dec 2013). "An estimation of the number of cells in the human body". Annals of Human Biology. 40 (6): 463–471. ↵
- Population of the United States ↵
- World population ↵
- Mass of a human cell ↵

