CHAPTER 1: NUMBER SENSE
1-5 The Order of Operations
The Order of Operations
Scenario 1
Jack walked into a restaurant. He asked the hostess where the kitchen was. He walked into the kitchen and asked the chef to make a meal for him. Then, he walked into the dining room and sat down at a table that had a tag saying “Reserved” on it and waited for his meal to arrive.
It turned out that Jack did not get his meal. Instead, Jack was escorted out of the restaurant.
Why did Jack not get his meal? Jack did not follow the order of operations for life. The order of operations for ordering a meal in the restaurant could be this: Ask to be seated, tell the server what you would like to eat when they visit your table, eat your meal when it is brought to you, ask for your bill, pay your server or the cashier.
Scenario 2
Leslie’s alarm went off and it was time to get up. They got out of bed, took off their pjs and started to get dressed. They put on a shirt and a pair of pants, then their socks and underwear. Then they walked into the bathroom to brush their teeth and take a quick shower. Leslie was ready for the day!
Was Leslie really ready for the day? Leslie did not follow the order of operations for getting up in the morning. They should have gotten out of bed and started in the bathroom. After removing their pjs they should have brushed their teeth then taken a shower (or vice versa). Getting dressed, they should have started with their underwear and socks, then added a shirt and pants. Then they would have been ready for the day!
In many real-life situations, we need to know the order of operations (e.g., cooking, baking, driving, construction, …) in order to do things safely, correctly, or considerately, and get things done. In mathematics, we also need to know the order of operations for arithmetic so that we perform computations correctly.
The Emergence of the Order of Operations in Arithmetic
What is formally called, the order of operations in mathematics (also referred to as operator precedence) has been around since the 16th and 17th centuries when exponents were first introduced. Order of operations started to show up in textbooks in the late 1800s, was still being debated in the 1920s, and was basically agreed upon in the 1960s. It is a set of rules that reflect conventions about which arithmetic and algebraic procedures need to be performed first to evaluate a mathematical expression. The conventions were agreed upon to eliminate notational ambiguity, to keep notation as brief as possible, and to improve mathematical communication.
The order of operations is defined by the precedence of the operators. Addition and subtraction are at the lowest, most basic level. Subtraction is simply addition of the opposite, so subtraction can always be written as addition. Multiplication is repeated addition, and division is multiplication of the reciprocal. So, division can always be written as multiplication. Multiplication is at the second level. Exponents indicate repeated multiplication, so exponents are at the 3rd level. The order of operations works from the highest level down, so exponents are calculated before multiplication, which is calculated before addition. Grouping symbols like parentheses ( ), brackets [ ], and braces { } are used to group terms together and signify that the operations inside them must be completed first as a unit. So, all we must remember is Grouping, Exponents, Multiplication, then Addition (GEMA).
The Order of Operations: GEMA
The order of operations is used to complete arithmetic operations in the correct order.
Grouping–work inside grouping symbols like ( ), [ ], and { } first following GEMA
Exponents–evaluate exponents next
Multiplication–evaluate multiplication and division from left to right
Addition–evaluate addition and subtraction from left to right
According to Pew Research[1], 96 percent of US adults aged 18 – 29 own a smartphone. That means that they own a calculator! Calculators are tools and we need to learn how to use them. The calculator will only give us the answer to the information we input through the buttons we push. The adage of “garbage in-garbage out” still prevails, so knowing how to input information correctly is key. But we also need to use reasoning and common sense to know whether our calculation is correct. Having a rough idea of what the answer should be and whether the answer makes sense will help us get to the correct answer.
 Parentheses
Parentheses
Explore 1 – Parentheses
John’s sister asks him to use a calculator to help double check her homework question:
![]()
John picked up a calculator and input: ![]()
Will he get the correct answer? Explain your reasoning. Test this on your calculator.
Solution
John’s answer was 1.625, which is incorrect. But how do we know it was incorrect? Calculators have the order of operations programmed into them, so when the calculator saw ![]() it followed the order of operations. The operations input into the calculator are subtraction (addition of the opposite) and division (multiplication by the reciprocal), so, since division is of higher priority than subtraction, the calculator divided first:
it followed the order of operations. The operations input into the calculator are subtraction (addition of the opposite) and division (multiplication by the reciprocal), so, since division is of higher priority than subtraction, the calculator divided first:
![]()
To get the correct answer, parentheses must be included around the numerator and denominator so that the calculator knows to complete the operation of subtraction on each of the numerator and denominator first before completing the division.
To input this question correctly, John needs to use a pair of parentheses to group ![]() on the numerator and
on the numerator and ![]() on the denominator so that numerator and denominator are evaluated before they are divided. This is because the priority of the grouping symbol parentheses and the operations inside the parentheses are higher than any objects and operations outside the parentheses.
on the denominator so that numerator and denominator are evaluated before they are divided. This is because the priority of the grouping symbol parentheses and the operations inside the parentheses are higher than any objects and operations outside the parentheses.
To correct his work, John should input,
![]()
This will result in the correct answer 0.4.
Explore 2 – Consecutive multiplications or divisions of numbers
John learned from his mistakes. This time John uses a pair of parentheses to input the following operation into his calculator.
![]()
- John said he can simplify the question first by dividing 4 by 2 and get
![]()
2. John then inputs
![]()
Will he get the correct answer? Explain your reasoning.
Solution
Unfortunately, John got it wrong again. First, John should not simplify by dividing 4 by 2 because 4 needs to be grouped with (10-6). When there are more than two or more consecutive multiplications or divisions or multiplication and division combined, the operations should be performed from the left to the right. Therefore, the multiplication ![]() will be performed first, and the the result will be divided by 2.
will be performed first, and the the result will be divided by 2.
Second, according to the order of operations, in his input 1 is grouped with 2 because the priority of division is higher than addition. Therefore, the operations John performs are different from the question. The operations the calculator performs are:
![]()
To fix the two mistakes, John should not simply by dividing 4 by 2. Also, John needs another pair of grouping symbols to include ![]() as part of the numerator. Since the numerator already includes a set of parentheses, John can use another type of grouping symbols, brackets:
as part of the numerator. Since the numerator already includes a set of parentheses, John can use another type of grouping symbols, brackets:
![]()
The brackets enclose the operations ![]() and these operations must be performed first following GEMA, before being divided by 2. This puts all operations on the numerator inside the brackets and 2 on the denominator.
and these operations must be performed first following GEMA, before being divided by 2. This puts all operations on the numerator inside the brackets and 2 on the denominator.
Although using brackets [ ] to enclose parentheses ( ) is mathematically correct when we are writing math, most calculators just use multiple sets of parentheses. Consequently, John’s calculator input should be,
![]()
The correct answer is ![]() .
.

- Why do we use parentheses in numerical expressions?
Show/Hide Answer
Parentheses are used to group specific operations together. They are also used to group operations on a numerator or a denominator of a division problem.
- Why are different types of grouping symbols used (e.g., parentheses and brackets)?
Show/Hide Answer
When writing grouping symbols within grouping symbols (nested grouping), different grouping symbols are used to make the expression easier to read. Parentheses ( ) are placed within brackets [ ] which are placed within braces { }. It just makes it easier to see when a expression that is grouped begins and ends.
 Evaluating Exponents
Evaluating Exponents
Explore 3 – Exponents
The population of a certain bacteria that loves cheese doubles twice per hour when the temperature is around 75oF. If a cheese that has 1 bacterium is left out of the fridge on a warm day, what is the number of bacteria on the cheese after 5 hours?
One student used the calculation,
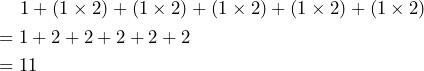
Is the student’s answer correct? Explain your reasoning.
Solution
The student’s answer is not correct.
The mistake the student made is that the doubling process is based on the initial number of bacteria (i.e., 1 bacterium). The correct process should be that the doubling process is based on the current number of bacteria. To illustrate, after one hour, the number of bacteria is ![]() . For the next hour, the doubling process is based on the current number of bacteria that is 2. Therefore, after two hours, the number of bacteria is
. For the next hour, the doubling process is based on the current number of bacteria that is 2. Therefore, after two hours, the number of bacteria is ![]() .
.
The doubling process across the five hours is illustrated in figure 1.
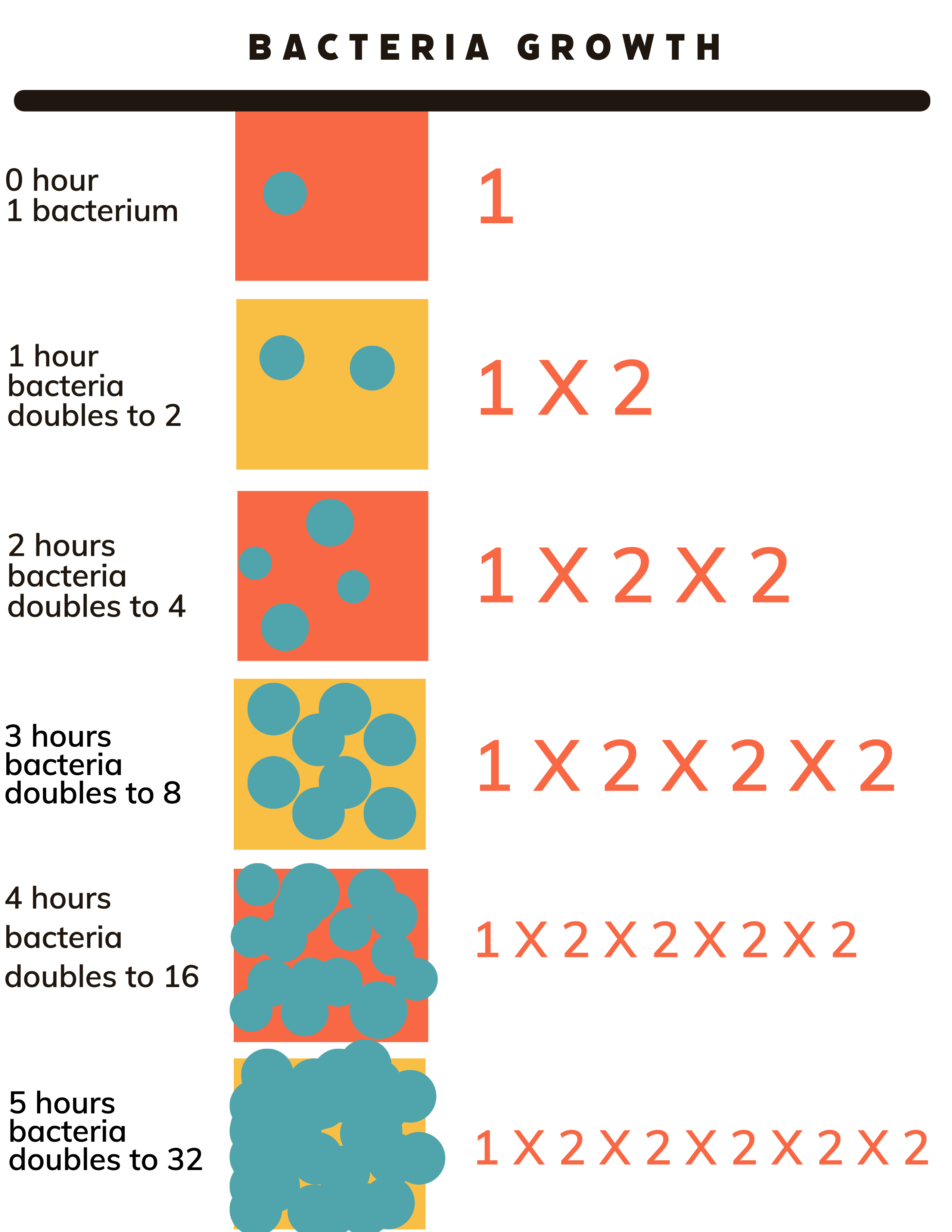
Since we are multiplying by 2 every hour, a pattern arises.
After 5 hours, the number of bacteria is ![]() .
.
To calculate this on a calculator, we use the exponent key.
The exponent key will either look like a carat ![]() or an exponential expression
or an exponential expression ![]() or
or ![]()
To input ![]() we type:
we type: ![]() and get an answer of 32.
and get an answer of 32.
Alternatively, we type: ![]() and get the same answer.
and get the same answer.
It is very important that you get to know your calculator. Don’t assume that you will automatically get the correct answer. Remember, garbage in; garbage out!
Explore 4 – Exponents
Following Explore 3, if a cheese that has 8 bacteria is left out of the fridge on a summer’s day, what is the number of bacteria on the cheese after 5 hours?
One student used the calculation,
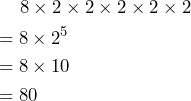
Is the student’s answer correct? Explain your reasoning.
Solution
The students’ answer is not correct. The correct answer is:
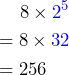 .
.
The mistake the student made is that the student multiplied the base of the exponential expression 2 by the exponent 5. The student should instead perform the exponential expression ![]() first, and then multiply 32 by 8.
first, and then multiply 32 by 8.
To put the expression ![]() into a calculator, we input
into a calculator, we input ![]() and get the answer 256.
and get the answer 256.

- What is the purpose of exponents?
Show/Hide Answer
Exponents represent repeated multiplication by the same number. The base tells us which number is being multiplied each time and the exponent tells us how many times to multiply the base by itself. Exponents are a shorthand way of writing multiple multiplication of the same number.
- How do exponents fit into the order of operations?
Show/Hide Answer
Exponents are evaluated first after all expressions inside grouping symbols have been taken care of.
Practice Exercises
Write out exactly what you would input into the calculator to evaluate each expression:
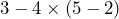
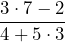
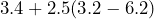
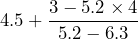
- Bailey received her city utilities bill in the mail.
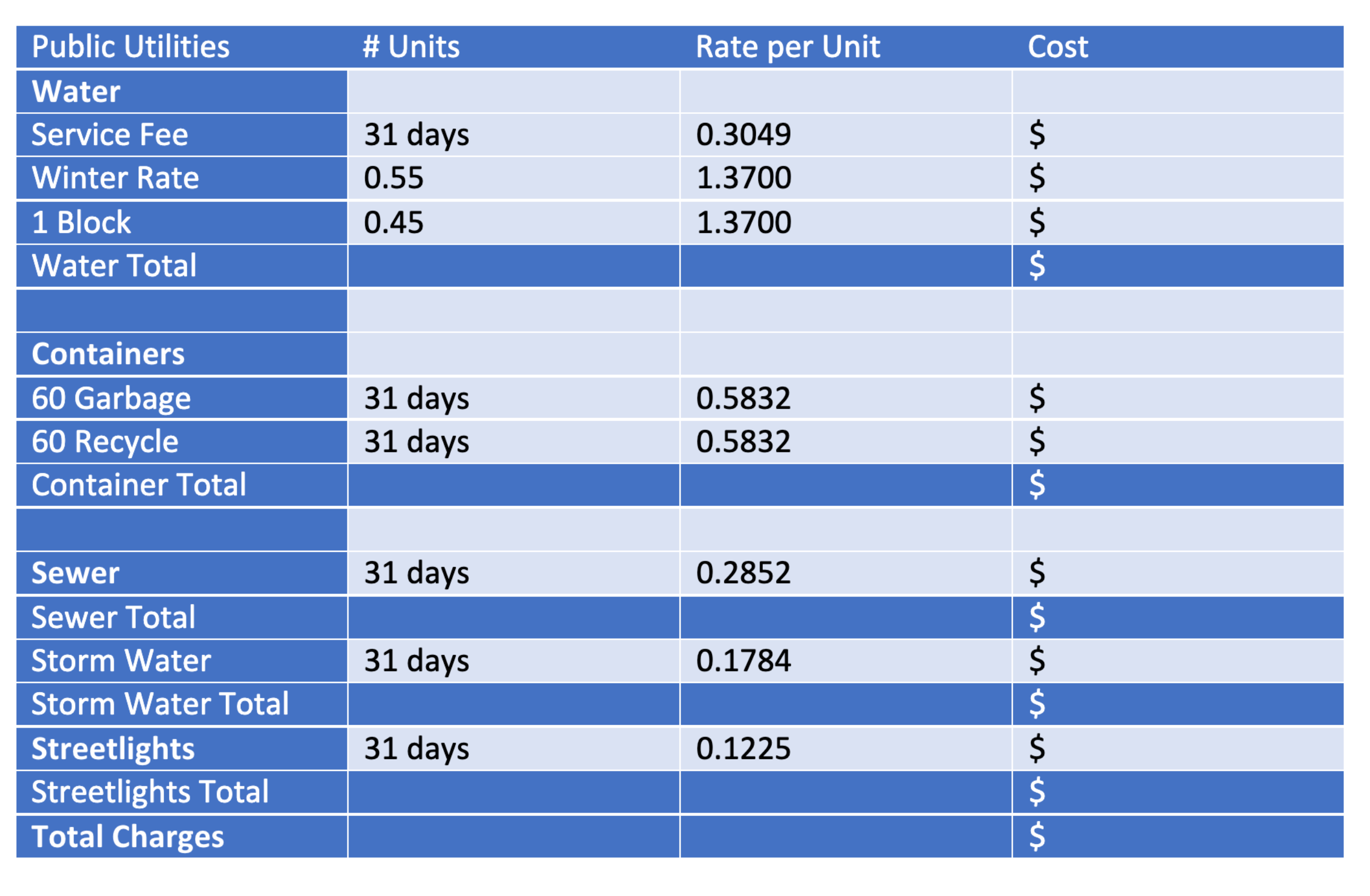
The utility bill contains the following information. For the water portion: Service Fee, 31 days at a rate of $0.3049 per day, .55 days at the winter rate of $1.3700 per day, .45 days at a rate of $1.3700 for a block fee. For a container fee: 60 gallon garbage container, 31 days at a rate of $0.5832 per day, 31 days at $0.5832 per day for a 60 gallon recycling container. For sewer: 31 days at a rate of $0.2852 per day. For storm water: 31 days at $0.1784 per day. For Street lights: 31 days at $0.1225 per day.
- What utilities are included in this bill?
- What measurement unit is the column rate per unit measured in?
- Calculate the cost column values in the table and calculate the total charges based on the information in the table.
- How many decimal places are there after the point for the total charge?
- What would you round the total charges to? Explain your reasoning.
Show/Hide Answer
-
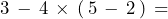
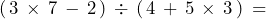
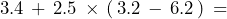
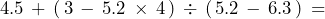
- a) The utilities covered in this bill are water, containers (garbage and recycling), sewer, storm water, and street lights.
b) The measurement unit for this column is not given. However, since we are looking at cost it makes sense that it is in $ per unit. For example, the water service fee has a units of days so the rate per unit would be $ per day.
c) The cost of water is made up of three sections: service fee + winter rate + blocks of water used. Therefore, the total cost will be the sum of the costs for each of these sections. Each separate cost can be calculated by multiplying the #units by the cost per unit.
Water total
Container total
Sewer total
Storm water total
Streetlights total
Therefore, Total charges = $10.8219 + $36.1584 + $8.8412 + $5.5304 + $3.7975 = $65.1494
d) There are 4 decimal places after the point.
e) $65.1494 would be rounded to $65.15 since there is no way to pay a value less than 1 cent. The digit 9 following the 4 in the cents place is greater than or equal to 5, so the 4 gets rounded up to 5.
 In this section, we will use order of operations to solve realistic problems.
In this section, we will use order of operations to solve realistic problems.
Perspectives
- When banks calculate interest they use the formula
![]()
A formula is just a rule that tells us how to combine numbers. Since the numbers in a formula can change depending on the situation, we use letters to denote these variable numbers. As such, these letters are called variables. In this formula, the variable ![]() stands for account balance,
stands for account balance, ![]() stands for principal (the initial deposit),
stands for principal (the initial deposit), ![]() stands for yearly interest rate, and
stands for yearly interest rate, and ![]() stands for the number of years the principal is invested. If we know the value of each variable we can rewrite the formula substituting given values for the variables.
stands for the number of years the principal is invested. If we know the value of each variable we can rewrite the formula substituting given values for the variables.
Suppose ![]() ,
, ![]() , and
, and ![]() . The only unknown variable value is
. The only unknown variable value is ![]() .
.
Tammy inputs the given numbers into the formula: ![]()
then uses her calculator as follows:
![]()
Will Tammy get the correct answer? Explain your reasoning.
- Every book published is assigned a unique International Standard Book Number (ISBN), which, since January 1st, 2007, consists of 13 digits.
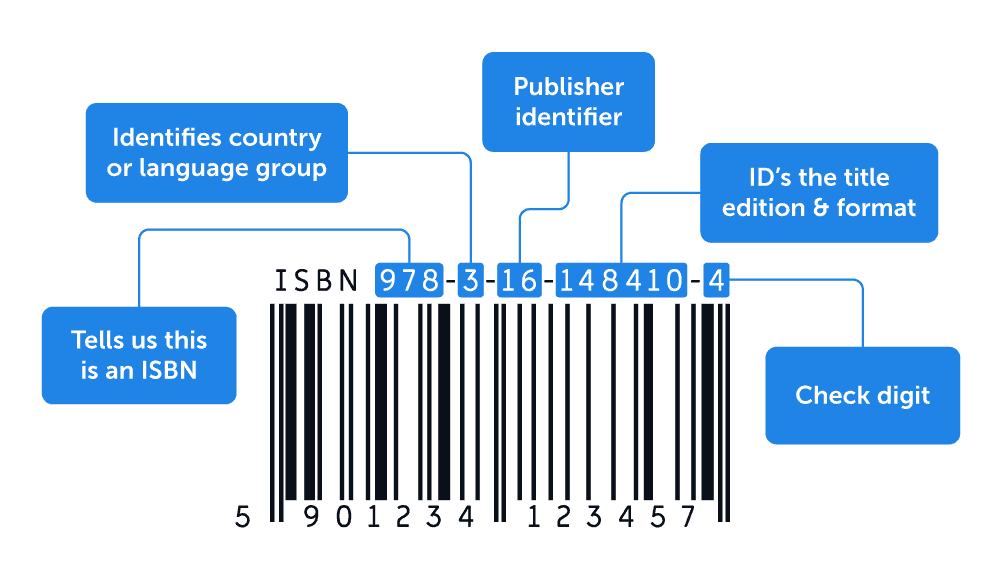
The last digit is called a check digit and is used to make sure there are no errors in the first 12 digits. The check digit is calculated by multiplying each of the first 12 digits by alternating weights of 1 and 3, adding the products up, then finding the remainder when that sum is divided by 10.
Write the operations to generate the checking digit.
b) Calculate the check digit. Is the check digit correct in this example? Explain your reasoning.
c) Find the check digit X for the ISBN 979-54-38602-04-X.
Show/Hide Answer
- No. Tammy will not get the correct answer. Following the order of operations, the correct answer is:
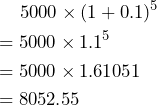
Tammy made a mistake. Tammy should have used a pair of parentheses to enclose the operation ![]() so that the number 1 was added to 0.1 instead of being multiplied by 5000. In the order of operations, operations inside parentheses have higher priority than any operations outside the parentheses. Therefore, 1 should be added to 0.1 first. After evaluating the operation inside the parentheses, we get 1.1. The exponential expression
so that the number 1 was added to 0.1 instead of being multiplied by 5000. In the order of operations, operations inside parentheses have higher priority than any operations outside the parentheses. Therefore, 1 should be added to 0.1 first. After evaluating the operation inside the parentheses, we get 1.1. The exponential expression ![]() should then be evaluated because the priority of exponents is higher than the associated multiplication (i.e., multiplied by 5000).
should then be evaluated because the priority of exponents is higher than the associated multiplication (i.e., multiplied by 5000).
The correct input is ![]() and the correct answer is 8052.55. Consequently, the account balance after 5 years would be $8052.55.
and the correct answer is 8052.55. Consequently, the account balance after 5 years would be $8052.55.
- a) The operations for generating the checking digit are:
![]()
Alternatively, ![]()
b) The calculation is ![]() .
.
The remainder when 10 is divided by 10 is 0. Therefore, the check digit is 0. The check digit on the picture of the ISBN is incorrect.
c) The operations for generating the check digit X for the ISNB 979-54-38602-04-X are:
![]()
or, ![]()
The calculation is:
![]() .
.
The remainder is 1. Therefore, the check digit X is 1.
Decimal numbers are everywhere. Any time you make a purchase you are using decimals. Any time you fill up your car with gas the pump shows how much gas you have pumped and how much it costs as decimals. Vehicle odometers use decimals. GPAs are decimals. Athletics use decimals both as distances for races and times. Our counting system is base-10 which extends to the decimal digits. We have 10 fingers so working with decimals makes perfect sense.
 In this section, we will use what we have learned so far to practice skill problems and strategies for solving them.
In this section, we will use what we have learned so far to practice skill problems and strategies for solving them.
Skills Practice
Use a calculator to evaluate each numerical expression.
- 1.
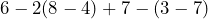
- 2.
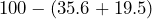
- 3.
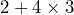
- 4.
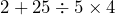
- 5.
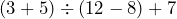
- 6.
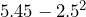
- 7.
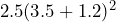
- 8.
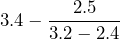
- 9.
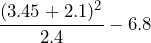
- 10.
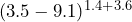
Show/Hide Answer
-
- 9
- 44.9
- 14
- 22
- 9
- –0.8
- 55.225
- 0.275
- 6.034375
- –5507.31776
The order that has been established to complete arithmetic operations. i.e. Grouping; Exponents; Multiplication; then Addition.
writing grouping symbols within grouping symbols e.g. {2 [3 · 4 – 5 (3 – 7)]}
a mathematical relationship or rule expressed in symbols
a symbol that represents a quantity in a mathematical expression that can be changed
One of the numbers 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 used in the decimal number system.

