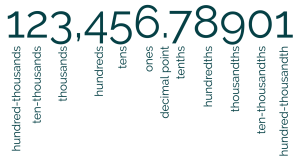1-0: Numbers in the Real World

A Quick History of Numbers    

Arithmetic is the oldest form of mathematics. It is the theory of the construction and manipulation of number systems. Humans started counting with tally sticks where marks or notches were made into sticks, bones, or antlers. These may have been used to count the passage of time in days or lunar cycles, or as a way to count animals. The Lebombo bone was discovered in Swaziland and is the oldest mathematical relic dating to around 44,000 BCE.

Counting systems developed independently across the world, most notable in Babylonia, South America, China, India, and Greece.

But tally sticks only counted. They were not numbers as we know them today where numerals and place-value are required for adding, subtracting, multiplying and dividing. The first known system with place value was the Mesopotamian base 60 system (c. 3400 BCE) and the earliest known base 10 system dates to 3100 BCE in Egypt. Numbers can use any base as their place-value. For example, the Mayans used base 20, and modern computers use base 2 (binary), base 8 (octal), or base 16 (hexadecimal) with an occasional base 3 (ternary) thrown in.

A Quick History of Arithmetic through Real Numbers

Humans started to count using what we know as the Natural Numbers: . Natural numbers could be added and multiplied within the natural numbers system but could not always be divided or subtracted. Think about or or ; none of these examples can be evaluated using only natural numbers.

The concept of zero may seem intuitive to us but that is because we are familiar it. The first evidence we have of zero is from the Sumerian culture in Mesopotamia, some 5,000 years ago when scribes left spaces to show absences in number columns. Much later, around the 3rd century BCE, the first recorded use of a zero-like symbol was introduced by the Babylonians. This symbol was a slanted double wedge that was inserted between cuneiform symbols for numbers, written positionally, to indicate the absence of a number in a place (as we would write 102, the ‘0’ indicating no digit in the tens column). A similar type of symbol cropped up independently in the Americas sometime around A.D. 350, when the Mayans began using a zero marker in the form of a shell-like symbol in their calendars. ^[1][2] Zero was not treated as a number in its own right but was seen as simply a placeholder digit or as a symbol for lack of quantity. The concept of zero as a written digit in the decimal place value notation was developed in India where a large dot was used to denote zero as a number in the Bakhshali manuscript dated to between 224 AD and 383 AD. ^[3][4] The earliest known text to consider arithmetic rules for zero as a number is Brāhmasphuṭasiddhānta, written by the Indian mathematician Brahmagupta around 628.^[5] However, the belief in zero as a number was considered heresy by the early Christian church and it wasn’t until the 12th century that the number zero was accepted in Europe.

The introduction of  negative numbers as early as 100–50 BCE in China, to deal with problems such as was also a concept that was not immediately accepted. European mathematicians, for the most part, resisted the concept of negative numbers until the 17th century and it wasn’t until the 19th century that the problem of negative numbers was resolved! ^[6]

These new ideas led to the Whole Numbers , the Integers and the Rational Numbers, which are all the numbers that can be written as fractions with a non-zero denominator using integer values.

To solve the division issue within whole numbers, Ancient Egyptians introduced positive fractions around 1850 BCE so that . The earliest known use of Irrational Numbers (numbers that cannot be written as a fraction with integer numerator and denominator) was in the Indian Sulba Sutras composed between 800 and 500 BCE. Geometry led to the first proof of the irrational number by Pythagorean Hippasus of Metapontum. ^[7] Rational and irrational numbers were then combined to form the Real Numbers. Notice how these numbers interact with each other: Natural Numbers are Whole Numbers are Integers are Rational Numbers are Real Numbers. Figure 2 shows this relationship.

What about Decimal Numbers? Decimal numbers are an extension of the place-value system of whole numbers. Digits to the left of the decimal point denote the integer part of the number, while digits to the right of the decimal point denote the fractional part of the number. Decimal numbers that either stop or have a repeating decimal after the point that goes on forever are rational numbers. Irrational numbers are represented by decimals that go on forever after the decimal point but never end in repeating digits. Consequently, all Real Numbers can be written as Decimal Numbers.

Place-Value 

Today, the most common numeral system is the Hindu–Arabic numeral system, which allows for the representation of any number using a combination of ten fundamental numeric symbols, called digits: . To count past 9, we need a place-value system that allows us to use the same digit to mean different things in a number. In a base-ten system, digits to the left are 10 times larger in place value than the adjacent digit to the right (figure 3). For example, or, using the place value names, 4 thousands + 4 hundreds + 4 tens + 4 ones.

Likewise, can be expanded to 5 tenths + 8 hundredths + 2 thousandths, and can be written 3 ones + 9 tenths + 5 thousandths.

Numbers in the Real World

In the real world, numbers do not exist in isolation. Rather, they are inextricably linked to the context in which they exist. No one would go into a store to buy 3 at a price of 12 per pair. The context is completely lost. But if someone were go into a store to buy 3 pairs of gardening gloves at $12 per pair, we now know the context to which the numbers belong. This first chapter will expose you to numbers used in context and the common sense and reasoning required to understand them. 

Numbers are used to count, label, measure, and calculate.

Numbers Used to Count

Based on the USDA, NASS 2017 Census of Agriculture, the average beef cow herd is about 44 head (USDA) [8]. The number 44 is a count of the number of beef cows in an average herd.

Numbers as Labels

When numbers are used as labels, there is no numeric order to the number.

Numbers as Measures

Numbers are used as measures when there is a unit of measurement associated with them.

Numbers to Calculate

Calculating takes place when numbers are combined through an arithmetic operation like adding or dividing.

The receipt shows a calculation where the cost of the juice ($5.00) is added to the cost of the sandwich ($4.99) to get a total for food of $9.99. Tax ($0.70) is then added to get a total payment of $10.69. The arithmetic calculation is $5.00 + $4.99 + $0.70 = $10.69

But be careful, for not all numbers that we still use today are base 10!

Roman Numerals

Although we typically use the digits 0-9 to write numbers, the use of Roman numbers still shows up here and there. Roman Numerals originated in ancient Rome (753 BC–476 CE) and remained the usual way of writing numbers throughout Europe well into the 15th century. Roman numerals, as used today, are based on seven symbols:

Numbers are formed by combining symbols and adding or subtracting the values depending on position. If the smaller valued symbol comes before a larger valued symbol, the value is subtracted. Otherwise it is added. For example, III equals 3 and XI equals 10 + 1 = 11, while XL equals 10 before 50 or 50 – 10 = 40 and MMCCIX equals 2(1000)+2(100)+(10-1)= 2209.

Today, the use of Roman Numerals is much more limited. Mostly they are used for show.

Time

When it comes to time, we use a base-12 or base-24 system. For example, 3 a.m. is equivalent to 0300 hours in military time, while 3 p.m. is equivalent to 1500 hours. Note that a.m. is the abbreviation for the Latin ante-meridiem (before noon) and p.m. is post-meridiem (after noon).

Minutes and seconds use base-60 since there are 60 seconds in a minute and 60 minutes in an hour. So 11:30:56 is 56 seconds past 11:30 or the race was run in 11 hours 30 minutes 56 seconds.

US Customary Measurements

When it comes to measuring length in the U.S., we have miles, yards, feet, and inches with 12 inches in a foot; 3 feet in a yard; 1780 yards in a mile! Then there’s weight with 16 ounces in a pound and 2000 pounds in a ton. But wait, there’s more! How about 16 fluid ounces in a pint; 2 pints in a quart; 4 quarts in a gallon. We won’t worry about such things right now, but you can see why the base-10 metric system is so much easier!

Numeracy

This book will take you on a journey through different types of numbers and how they are used in everyday life. We assume that you are familiar with the basics of place-value and arithmetic of whole numbers. We will start with a brush up of integers then move on to decimals. We also assume that you have seen integers, fractions and decimals at some point in your life, but we recognize that you may not be too comfortable using them. This book will not give you a list of rules to memorize. Rather it will provide you with examples and opportunities to learn how numbers are used and ask you to formulate your own thoughts. We want you to become comfortable with numbers and think about the relationship numbers have with the everyday world. We want you to problem solve. We hope that by presenting topics in a way that is different from what you’ve seen before that you will appreciate what math offers in life. We expect that you will become confident in your own ability to use numbers, that you will become numerically literate, and not fall into the traps laid for the innumerate in society.