2 The Biases and Fallacies of Homo sapiens

The quirks discussed in Chapter 1 set the stage for biases and fallacies that often plague the choice behavior of Homo sapiens. The extent to which we miscalculate problems—problems begging for various degrees of logical reasoning—illuminates our inherent cognitive limitations. The effects that prime and frame us to miscalculate and misjudge underlying conditions (or when harnessed for our betterment, help us correct our otherwise misguided thought processes) evince the different contexts within which our quirks lead us astray. As we learned in Chapter 1, Homo sapiens have devised heuristics, or rules-of-thumb, that we use as substitutes for deeper analysis of, or reasoning about, problems that otherwise warrant such depth and reasoning.

In this chapter, we make a subtle turn from these stage-setting quirks toward identifying the different ways in which Homo sapiens are innately biased. The word “innately” is important here. Bear in mind that the biases discussed in this chapter are, for the most part, ingrained in the human condition. They are not learned prejudices.

Status Quo Bias

As previously discussed in Example 3 in the Introduction, Homo sapiens are prone to what’s known as Status Quo Bias, whereby we tend to resist change, and thus, sometimes miss opportunities to make beneficial changes in our personal lives as well as those for society at large. In Example 3 we learned that choosing the default option carefully can solve the problem of status quo bias. For instance, the nations of Spain, Belgium, Austria, and France have among the highest organ donation consent rates. Why? They use “opt-out” default on the organ donation registration form, and thus, presume consent on the behalves of their citizens (Davidai et al., 2012). Similarly, Thaler and Benartzi (2004) proposed the Save More Tomorrow (SMarT) Program where employees commit in advance to allocate a portion of their future salary increases toward retirement savings (in effect opting out of the alternative of not making this allocation). The authors found that (1) 78% of the company’s employees offered the plan joined, (2) 80% remained in the program for 40 months, and (3) the company’s average savings rate increased by 10%.

Confirmation Bias

In our daily lives, we sometimes guard more against committing what Statisticians call Type 2 error (failing to reject a false null hypothesis) than against committing Type 1 error (rejecting a true null hypothesis). For example, one of my most frequent Type 2 errors is instinctively blaming my wife whenever something of mine goes missing at home, like a pair of shoes or a magazine. In this case, I effectively set the null hypothesis as “my wife is innocent.” In my mind though, I consider her guilty. I am therefore afraid of failing to reject the null hypothesis that she is innocent. Further, I unwittingly guard my ego against being proved wrong by sharing menacing looks and grimaces and sighs of helplessness. This is my guard against committing what I suspect would be a Type 2 error. Unfortunately, this precautionary tendency leads me to commit what is known as Confirmation Bias.[1] The way I structure my thinking, and the way I behave, impel me to confirm to myself that I am not absent-minded. It’s my wife’s fault. She is the guilty one!

Darley and Gross (1983) conducted one of the earliest and most enduring studies of Confirmation Bias with approximately 70 of their undergraduate students. One subgroup of the students was subtly led to believe that a child they were observing came from a high socio-economic (SE) background, while another subgroup was subtly led to believe that the child came from a low SE background. Nothing in the child’s SE demographics conveyed information directly relevant to the child’s academic abilities. When initially asked by the researchers, both subgroups rated the child’s ability to be approximately at grade level. Two other subgroups, respectively, received specific SE demographics about the child—one set of demographics indicating that the child came from a high SE background, the other that she came from a low SE background. Each of these two subgroups then watched the same video of the child taking an academic test. Although the video was identical for all students in these two subgroups, those in the subgroup who had been informed that the child came from a high SE background rated her abilities well above grade level, while those in the subgroup for whom the child was identified as coming from a lower SE background rated her abilities as below grade level. The authors concluded that Homo sapiens are prone to using some “stereotype” information to form hypotheses about the stereotyped individual. Homo sapiens test these hypotheses in a biased fashion, leading to their false confirmation.

Law of Small Numbers

Consider the following thought experiment presented in Kahneman (2011):

Consider three possible sequences for the next six babies born at your local hospital (B stands for “boy” and G stands for “girl”):

B B B G G G

G G G G G G

B G B B G B

Are these sequences equally likely?

Kahneman’s guess is that you answered “no,” in which case you consider the third sequence (B G B B G B) to be the most likely to occur. You liken it to your experience flipping a coin—flip the coin often enough and you would expect to see Heads and Tails alternating more repeatedly, which would be a valid expectation. The problem here is that the coin hasn’t yet been flipped often enough. A sequence of six babies is not enough flips of the coin, so to speak, to necessarily start witnessing an alternating pattern. Hence, if you indeed answered “no” to the question you are guilty of what’s known as the Law of Small Numbers.[2] Needless to say, Homo economicus is not beholden to this law.

In a classic study of the Law of Small Numbers, Gilovich, et al. (1985) investigated common beliefs about “the hot hand” and “streak shooting” in the game of basketball. The authors found that basketball players and fans alike tend to believe that a player’s chance of hitting a shot is systematically greater following a hit than following a miss on the previous shot. However, data compiled for an entire season (i.e., data from a large sample) did not support the hot-hand hypothesis which, by its very nature, is predicated on a game-by-game basis (i.e., data from a small sample).

In specific, Gilovich, et al. (1985) found that if a given player on a given night had just missed one shot, then on average, he hit 54% of his subsequent shots. Likewise, if the player had just hit one shot, he hit 51% of his remaining shots. After hitting two shots, he then hit 50% of subsequent shots. The estimated correlation coefficient between the outcome of one shot and the next was a statistically insignificant −0.039, suggesting that shooting streaks are an illusion. Each shot is essentially independent of the previous shot. To the contrary, when surveyed, basketball fans on average expected a 50% shooter to have a 61% chance of making a second shot once the first was made. The authors also analyzed game-by-game shooting percentages to see if a player’s performance in a single game could be distinguished from any other game. Again, contrary to the beliefs of the average fan, they found no evidence that players have hot and cold shooting nights.[3]

Representative Bias

Consider the following two-part thought experiment presented in Kahneman (2011):

James is a new student at your university. What is the likelihood that James’ major is?

Psychology    Philosophy    Chemistry    Computer Sciences    Library and Info Sciences    Physics

Hopefully, you appealed to some base-rate information in answering this question, either because you recently happened to see some published statistics about your university’s distribution of majors or because you’ve wondered about this very question before and, based upon your perceptions, can guesstimate a fairly reasonable answer.

Now, consider a slightly altered form of this experiment.

James is a new student at your university. During his senior year of school his school’s psychologist made the following personality sketch of James based upon tests of uncertain validity:

“James is of high intelligence. He has a need for order and clarity, for neat and tidy systems in which every detail finds its appropriate place. His writing is rather dull and mechanical. He has a strong drive for competence. He seems to have little sympathy for other people and does not enjoy interacting with others. Self-centered, James nonetheless has a deep moral sense.”

What is the likelihood that James’ major is?

Psychology    Philosophy    Chemistry    Computer Sciences    Library and Info Sciences    Physics

Kahneman’s guess is that the added information provided by James’ high school psychologist has made it more likely that your ranking of the likelihoods of each candidate major looks something like this.

Chemistry   Physics   Computer Sciences    Philosophy   Psychology   Library and Info. Studies

In which case you would be guilty (justifiably so?) of what’s known as Representative Bias.

Conjunction Fallacy

Consider the following thought experiment proposed by Kahneman (2011):

Ella is 31 years old, single, outspoken, and very bright. She majored in Philosophy. As a student, she was deeply concerned with issues of discrimination and social justice, and also participated in the 2017 Women’s March in Washington, DC.

Referring to the list below (which is presented in no particular order), rank each statement from the most to least likely:

1. Ella is a teacher in a primary school.
2. Ella works in a bookstore and practices yoga.
3. Ella is active in promoting women’s rights.
4. Ella is a social worker.
5. Ella is a member of Equality Now.
6. Ella is a bank teller.
7. Ella is an insurance agent.
8. Ella is a bank teller and is active in promoting women’s rights.

If you ranked number 8 higher than numbers 3 or 6, then you are guilty of a Conjunction Fallacy. That is because numbers 3  and 6 are each marginal probabilities and number 8 is a corresponding joint probability. By definition, marginal probabilities are never less than corresponding joint probabilities. But not to worry. Kahneman reports that in repeated experiments, over 80% of undergraduate and graduate students at Stanford University make the mistake. Homo economicus? Never.

Conjunction Fallacy (Version 2)

As another example of the Conjunction Fallacy, consider the following thought experiment provided by Kahneman (2011):

Suppose I have a six-sided die with four green faces and two red faces, which will be rolled 20 times. I show you three sequences that could potentially arise during any subset of the 20 rolls (G = green and R = red):

1. R G R R R
2. G R G R R R
3. G R R R R R

Choose the sequence you think is most likely to have arisen during a subset of 20 rolls.

If you chose Sequence 2, you have unwittingly fallen victim to a Conjunction Fallacy. Note that Sequence 1 is a subset of Sequence 2. Similar to the marginal vs. joint probability comparison in the previous thought experiment, subsets of a larger set are always more likely to occur than the larger set itself. To derive this result mathematically, begin by noting that the probability of a red face occurring on any given roll of the die is 2/6 = 1/3 and the probability of a green face is 4/6 = 2/3. Since the outcome of each roll of the die is independent from the outcomes of any other roll, the probability of Sequence 1 is therefore 1/3 x 2/3 x 1/3 x 1/3 x 1/3 = 0.00823, and the probability of Sequence 2 is 2/3 x 0.00823 = 0.00549.

Guess who would have done this math in his or her head, and thus, never chosen Sequence 2?

Planning Fallacy

Kahneman (2011) recounts an anecdote about a company’s management team that had unfortunately developed over time a systematic tendency toward unrealistic optimism about the amount of time required to complete any given project, as well as the project’s probable outcome. Unrealistic optimism is a symptom of what is known as Planning Fallacy, which in turn results in Optimism Bias. As Kahneman (2011) informs us, one way to eschew this bias is to conduct a “premortem” before a project begins, whereby the management team imagines that the project has failed and then works backward (a technique known as backward induction, which you will learn more about in Section 3 of this textbook) to determine what could have potentially lead to the project’s failure. This strategy seems to align with the old adage, “hope for the best, expect the worst.”

Stereotyping

Consider the following thought experiment.

A Taxi in Yangon (the capital city of Myanmar) was involved in a hit-and-run accident at night. Two taxi companies, Grab and Hello, operate in the city.

You are given the following data:

•  The two companies operate the same number of taxis, but Grab taxis are involved in 85% of accidents.

•  A witness identified the taxi as Hello. The court tested the reliability of the witness under circumstances that existed on the night of the accident and concluded that the witness correctly identified each one of the two taxis 80% of the time and failed to identify them 20% of the time.

Q:  What is the probability that the taxi involved in the accident was Hello rather than Grab?

If you are like most people, you see this experiment as suffering from TMI. In your mind, the great majority of the evidence suggests that a Grab taxi was the culprit. Thus, although you might not assign a probability as low as 100% − 85% = 15% to a Hello taxi having been involved in the accident, chances are you will assign something close to 15%, in which case you are guilty of adopting an Availability Heuristic (recall the discussion about this heuristic in Chapter 1) and consequently stereotyping poor old Grab taxi company. Mathematically, we can use the information supplied in the thought experiment and appeal to what’s known as Bayes Rule to calculate Hello’s actual probability.

Let Pr(H) = 0.15 represent Hello’s (H’s) probability of getting in an accident on any given night.

Let Pr(G) = 0.85 represent Grab’s (G’s) probability of getting in an accident on any given night.

Let Pr(H|W) = 0.80 represent the probability that H was involved in the accident given the witness’s (W’s) testimony.

Let Pr(G|W) = 0.20 represent the probability that G was involved in the accident given W’s testimony.

Via Bayes Rule, the probability that a Hello taxi was involved in the accident is calculated as,

[Pr⁡(H|W) \, x \, Pr⁡(H)] \div [(Pr⁡(H|W) \, x \, Pr⁡(H))+(Pr⁡(G|W) \, x \, Pr⁡(G) )]

=[0.80 x 0.15] ÷ [(0.80 x 0.15)+(0.20 x 0.85) ]=41%,

which (surprise, surprise) is exactly the probability that Homo economicus would calculate.

Stereotyping does not materialize solely as a lack of application or misapplication of a mathematical rule. It is a much more pervasive behavior among Homo sapiens, particularly when it comes to ascribing motives to or judging the practices of other individuals or groups of people. How do we integrate our impressions of another person to form a perception of that individual’s reference group as a whole? To what extent does the Availability Heuristic lead to stereotyping in instances such as these?

Rothbart et al. (1978) preface their experiments in pursuit of answers to these questions with the basic understanding that among Homo sapiens information obtained about other individuals is organized mnemonically. Attendant judgments made about the other individuals’ respective reference groups in turn vary according to the way the information is organized in one’s brain. In particular, when we have repeated interactions with individuals of a specific group, we may organize our perceptions of this group around the specific individuals with whom we have interacted or around an integration of the repeated characteristics of the individuals we have encountered.

Further, Rothbart et al. postulate that one of the strongest determinants of mnemonic organization is the demand made on memory during the learning process. When there is low demand on memory, individuals can organize their perceptions of a group around their interactions with its individual members. However, under a high-memory load, individuals are more apt to organize their perceptions around the integration of repeated characteristics encountered within the group as a whole (ignoring the specific individuals encountered). To investigate these issues of memory, organization, and judgment driving Homo sapiens’ proclivity to stereotype, the authors designed a series of experiments to examine the effects of memory organization on the recall and heuristic judgments of a reference group’s characteristics.

In the experiments, over 200 subjects are presented with identical trait information about group members in one of two ways. In the single-exposure condition, each presentation of a trait is paired with a different “stimulus person,” where each stimulus person is encountered only once. In the multiple-exposure condition, a given trait (e.g., “lazy”) is paired multiple times with different stimulus persons. Eight favorable traits (cooperative, objective, intelligent, generous, creative, resourceful, sincere, reliable) and eight unfavorable traits (clumsy, anxious, impatient, lazy, compulsive, irritable, withdrawn, stubborn) were used in the experiments. Depending upon the particular experimental session, the same number of desirable traits were presented either one-third as often, half as often, or three-times more often than undesirable traits. The actual experiments themselves consisted of either 16 (low-memory load) or 64 (high-memory load) name-trait pairings.

After the presentation of the stimulus information, subjects estimated the proportions of desirable, undesirable, and neutral persons in the group, recalled the adjective traits, and rated the attractiveness of the group as a whole. Two measures of group attractiveness were obtained by asking subjects to rate the desirability of the group as a whole on a 17-point scale from 1 (extremely undesirable) to 17 (extremely desirable) and to rate “how much they would like a group with these characteristics to be among (their) close friends” on a 17-point scale from 1 (dislike very much) to 17 (like very much).

Rothbart et al. find that when under low-memory load and in the multiple-exposure condition, the typical subject’s recollection of desirable stimulus persons in the group, as well as his or her judgment of group attractiveness, both remained constant as the proportion of presentation of the same desirable stimulus persons increased. This means that if a new individual joined the multiple-exposure group, say Fred, who demonstrated two instances of generosity, then this would not alter the typical subject’s recollection and judgment of the group’s desirability. On the contrary, when the proportion of different desirable stimulus persons increased in the single-exposure condition, the subject’s judgment of group attractiveness increased proportionally (e.g., if sincere Sam was added to the single-exposure condition, the experiment’s typical subject would increase his or her judgment of group attractiveness, and this increased amount would itself increase as additional desirable stimulus persons were added to the group). When under a high-memory load, the subject’s recollection and judgment of the group’s desirability increased proportionately as desirable stimulus persons were added under either the single- or multiple-exposure condition.

Therefore, the authors conclude that subjects under low-memory load organize their perceptions of group desirability around the preponderance of desirable stimulus persons in the group, while subjects under high-memory load organize their perceptions around the group as a whole regardless of whether an increase in desirability materializes through the addition of single encounters with desirable stimulus persons (single-exposure condition) or multiple encounters (multiple-exposure condition). In other words, the extent to which Homo sapiens stereotype depends upon how loaded their memories are with interactions with different members of the group being judged.[4]

Conformity

In what has since been deemed a classic test of the social stigma of Conformity, Asch (1951) devised an experiment to test the extent to which a “naive subject” might choose to conform. In this experiment, the naive subject conforms when he selects an obviously wrong answer to a simple question as a result of having been unknowingly placed in a group of “stooges.” Stooges had been pre-programmed to select the obviously wrong answer en masse.

The experiment presents the naive subject with the following figure.

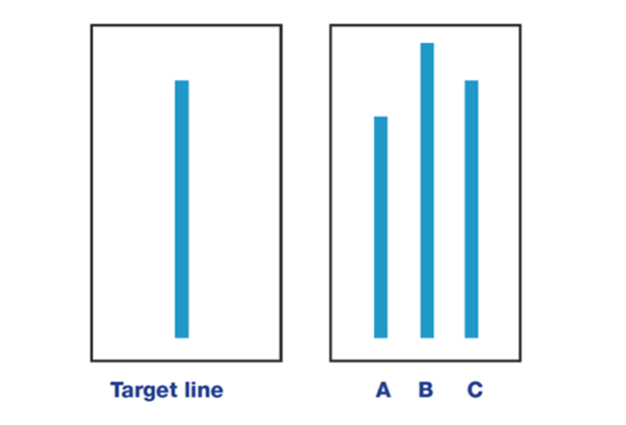
“Psychology-asch-1951“, by Saul McLeod, licensed under CC BY 3.0

He is then, eventually, asked which line in the box on the right—A, B, or C—is most like the Target line in the box on the left. Clearly, the correct answer is line C. However, in this experiment each of the stooges answers aloud and individually before the naive subject. In some treatment trials, each stooge answers line A, while in others they answer line B. The naive subject conforms if he answers line A in the former case and line B in the latter.

Asch (1951) conducted 18 trials total, 12 of which were treatment trials including stooges, and 6 of which were control trials without stooges (i.e., where no subjects in the group had been pre-programmed to say line A or line B). In the treatment trials, 75% of the naive participants conformed. In the control groups, only 1% of subjects gave incorrect answers (i.e., 99% of the subjects chose line C).[5]

What do you think would have been the outcome of this experiment if the naive subjects in the treatment groups would have been from the Homo economicus species rather than Homo sapiens?

Hindsight Bias

Fischhoff and Beyth (1975) engaged students at Hebrew University and Ben Gurion University of the Negev in Israel in an interesting experiment regarding the students’ predictions and recollections of then-President Nixon’s diplomatic visits to China and the USSR in the first half of 1972. It turns out that 75% of the students recalled having assigned higher probabilities than they actually had to events that they believed had happened. Specifically, shortly after Nixon’s visit to China or the USSR, these students erroneously believed that they had more accurately predicted before Nixon’s visit that Nixon would make the trip. And 57% of the students erroneously recalled having assigned lower probabilities than they actually had to events they believed had not happened. Specifically, shortly after Nixon’s visit to China or the USSR, these students erroneously believed that they had more accurately predicted before Nixon’s visit that Nixon would not visit somewhere else, other than China or the USSR. Ouch!

These exaggerations of predictive accuracy are reflective of what is known as Hindsight Bias.[6]

Less is More

Redelmeier et al. (2003) report on a study of roughly 700 patients who underwent colonoscopies. The patients self-reported the intensity of pain on a 10-point scale (0 = “no pain at all” to 10 = “intolerable pain”) every 60 seconds during the procedure. By random assignment, half of the patients’ procedures lasted a relatively short amount of time. The other half had a short interval of time added to the end of their procedure during which the tip of the colonoscope remained in their rectums (egad!).

The experience of each patient varied considerably during the procedure. As an example, suppose Patient A’s procedure lasted 14 minutes, while Patient B’s lasted 29 minutes. Later, shortly after their respective procedures, we would expect Patient B to have reported incurring more pain overall (again on a 10-point scale) since the “integral of pain” is larger for Patient B. On the contrary, the researchers found that on average those patients who underwent the extended procedure (like Patient B) rated their overall experience as less unpleasant than those who underwent the shorter procedure.[7] This result exemplifies what’s known as Less is More.

Flat-Rate Bias

Many services can be purchased on a per-use or flat-rate basis (e.g., per-month, per-season, or per-year). For example, mass transit in most cities can be paid for per ride or via a monthly or pre-paid transit pass. Health clubs allow you to pay per visit or on a monthly, annual, or punch-pass basis. Living in Utah where downhill skiing is considered by many to be a must-do, I can purchase a daily lift ticket each time I arrive at the mountain or pre-purchase a season’s pass which allows me unlimited visits during the ski season. It seems only logical that for purchases like these, people decide how many times they will use the service during a given year and then choose to purchase on a per-use or a flat-rate basis, whichever costs them less. But such is not always the case. Homo sapiens are prone to what’s known as Flat-Rate Bias.

For example, Della Vigna and Malmendier (2006) analyzed data from three U.S. health clubs with information on both the contractual choice and the day-to-day attendance decisions of approximately 8,000 members over three years. Members who chose a contract with a flat monthly fee of $70 attended on average 4.3 times per month. They, therefore, paid an effective price per visit of more than $17 even though they could have paid only $10 per visit using a 10-visit punch pass. On average, these members forgo savings of roughly $600 over the course of their memberships. Further, members who chose the monthly contract were 17% more likely to stay enrolled beyond one year than users pre-committing for a single year. Flat-Rate Bias, therefore, has relatively costly consequences for these members.

Della Vigna and Malmendier mention the leading explanations for their findings: overconfidence about future self-control and resolve. Overconfident members overestimate their future attendance as well as their resolve to cancel automatically renewed contracts. This latter manifestation of overconfidence—a lack of resolve when it comes to cancelling a contract—is what’s known as a time inconsistency problem (or a Projection Bias). Time inconsistency arises when you make a suboptimal choice in the moment that is inconsistent with how you envisioned making that choice at an earlier period in time (e.g., as part of a larger plan). For example, you may originally sign the contract with automatic renewal with the understanding that if later on you find yourself working out less than expected, you will cancel. But as “later on” becomes “today,” you’re just too busy or forgetful to follow through with the cancellation.[8]

Diversification Bias

As Read and Loewenstein (1995) point out, the rational model of Homo economicus’ choice behavior suggests that it is better to make choices in combination rather than separately, in other words, to frame the choices broadly rather than narrowly. For example, for dinner tonight, you should choose the restaurant you will eat at based upon the expected quality of the entrée, and then also envision the wine you will choose based upon the entrée. And before going out, you should select a matching outfit. It would probably be best if you combine the restaurant, dinner, wine, and outfit into a single interrelated choice. The advantages of a combined choice stem from the complementarities and substitutability between the individual choices. Only when choices are made in tandem can such interactions be accommodated optimally.

Previous experiments conducted by Simonson (1990) and Simonson and Winer (1992) found that if consumers combine their purchases at a single, initial point in time (to simultaneously provide for current and future consumption), they will choose more diverse bundles (i.e., exhibit more variety-seeking behavior) than if they make purchases sequentially at the various points in time when the goods are actually to be consumed. Homo sapiens being Homo sapiens, the question naturally arises as to whether consumers are prone to over-compensate when it comes to adding variety to their bundles. When consumers plan for more variety (in the simultaneous-choice setting) than they will subsequently desire (in the sequential-choice setting), they exhibit a Diversification Bias. Read and Loewenstein conduct a series of simultaneous- and sequential-choice laboratory experiments to explain potential underlying causes of this bias.

The authors identify a host of possible explanations for Diversification Bias stemming from (1) time contraction, when consumers subjectively shrink the inter-consumption interval when making an initial simultaneous choice, thus exaggerating the impact of satiation on their preferences, and (2) choice bracketing, when a simultaneous choice is presented to consumers in the form of a package and the most straightforward choice heuristic is to diversify.[9] In the experiments, roughly 375 subjects (undergraduate economics students at Carnegie Mellon University) are randomly assigned to groups tasked with making either simultaneous or sequential choices across three different snacks from among the following six: Snickers bars, Oreo cookies, milk chocolate with almonds, tortilla chips, peanuts, and cheese-peanut butter crackers. Read and Loewenstein ultimately find evidence of both time contraction and choice bracketing as underlying reasons for Diversification Bias.

The Bias Blind Spot

We conclude this chapter with a simple question (and provide a generally accepted answer to it). To what extent do Homo sapiens perceive themselves as less guilty of biasedness in their own thinking than others are in theirs—others such as the “average American” or “average classmate”? Pronin et al. (2002) couch this question of “asymmetry in perceptions of bias” as an informal hypothesis:

“People think, or simply assume without giving the matter any thought at all, that their own take on the world enjoys particular authenticity and will be shared by other openminded perceivers and seekers of truth. As a consequence, evidence that others do not share their views, affective reactions, priorities regarding social ills, and so forth prompts them to search for some explanation, and the explanation most often arrived at is that the other parties’ views have been subject to some bias that keeps them from reacting as the situation demands. As a result of explaining such situations in terms of others’ biases, while failing to recognize the role of similar biases in shaping their own perceptions and reactions, individuals are likely to conclude that they are somehow less subject to biases than the people whom they observe and interact with in their everyday lives.” (pp 369-370)

The authors label this asymmetry as a special case of “naive realism” called the Bias Blind Spot. To test their hypothesis, Pronin et al. surveyed a group of 24 Stanford students enrolled in an upper-level psychology class on their susceptibility to eight different biases compared with both the average American and their average classmate. The biases were associated with (1) self-serving attributions for success versus failure (Self-Serving), (2) reduction of cognitive dissonance after having voluntarily made a choice (Cognitive Dissonance), (3) the halo effect (recall our discussion in Chapter 1) (Halo Effect), (4) biased assimilation of new information (Biased Assimilation), (5) reactive devaluation of proposals made by one’s negotiation counterparts (Reactive Devaluation), (6) perceptions of hostile media bias toward one’s group or cause (Hostile Media), (7) the fundamental attribution error associated with blaming the victim (FAE), and (8) judgments about the greater good that are influenced by personal self-interest (Self Interest).[10]

The authors point out that while none of these particular biases had previously been discussed in the class, participants may have learned about some of them in other psychology courses. Further, the descriptions of the biases used the neutral terms “effect” or “tendency” rather than the nonneutral term “bias.” Thirteen participants were asked first about their susceptibility to each of the eight biases (“To what extent do you believe that you show this effect or tendency?”) and then about the susceptibility of the average American to each (“To what extent do you believe the average American shows this effect or tendency?”) The remaining 11 students rated the average American’s susceptibility before their own. Ratings were made on nine-point scales anchored at 1 (“not at all”) and 9 (“strongly”), with the midpoint of 5 labeled “somewhat.”

Pronin et al. found that for each bias the students on average rate their susceptibility less than what they perceive as the average American’s. For some biases (e.g., Self-Serving, FAE, and the Halo Effect), the difference is relatively large, while for others (e.g., Reactive Devaluation and Cognitive Dissonance), the difference is relatively small.[11] Interestingly, the students also rated their parents as less susceptible to each bias than the average American. In a separate study with a different sample of students, Pronin et al. find that, although not as strong, these results extend to the average student in another seminar course—a comparison group that is less hypothetical and more relevant to the participating students than the average American.

Alas, it appears that not only are Homo sapiens susceptible to a host of biases and fallacies and effects, but they are also susceptible to projecting their biases onto others, creating a ripple effect throughout society. This leads Pronin et al. to conclude that,

“In the best of all possible worlds, people would come to recognize their own biases and to recognize that they are no less susceptible to such biases than their adversaries. In the imperfect world in which we live, people should at least endeavor to practice a measure of attributional charity. They should assume that the “other side” is just as honest as they are (but not more honest) in describing their true sentiments—however much these may be distorted by defensiveness, self-interest, propaganda, or unique historical experience.”  (p 380)

Study Questions

Note: Questions marked with a “†” are adopted from Just (2013), and those marked with a “‡” are adopted from Cartwright (2014).

  1. † Homo economicus prefers information that is accurate no matter how it relates to her current hypothesis. She continues to seek new information until she is certain enough of the answer that the cost of additional information is no longer justified by its degree of uncertainty. As we know, Confirmation Bias among Homo sapiens can lead to overconfidence, which impedes the individual from fully recognizing the level of uncertainty she faces. What implications are there for an information search by individuals displaying Confirmation Bias? When do these individuals cease to search for additional information? What might this imply about people who have chosen to cease their education efforts at various phases? How might education policy be adjusted to mitigate this bias among individuals who terminate their educations at different levels (e.g., before earning an Associate’s or Bachelor’s degree)?
  2. Discuss how Status Quo Bias and the Mere Exposure Effect are related to each other.
  3. Explain how Status Quo Bias has a negative impact on your life. Can you think of an example of how this bias impacts your life positively?
  4. ‡ Why might the use of a heuristic stem from an underlying bias? Give an example of a heuristic presented in Chapter 1 that accompanies a bias presented in this chapter. Should we emphasize how clever people are for utilizing good heuristics or how deficient they are for being biased in the first place?
  5. Give an argument for why people who believe in extrasensory perception (ESP) or are prone to superstition are more likely to exhibit Confirmation Bias than people who are not.
  6. Why might people who are prone to Status Quo Bias also be prone to Confirmation Bias?
  7. Explain how Confirmation Bias both differs from and is similar to Jumping to Conclusions.
  8. As mentioned in the discussion of the Law of Small Numbers, basketball fans tend to believe they are witnessing a “hot hand” when a player makes a series of shots during a game. Gilovich, et al. (1985) dismissed the hot hand as a myth. Recall that based upon a season’s worth of data, the authors found that if a given player on a given night had just missed one shot, then on average, he hit 54% of his subsequent shots. Likewise, if the player had just hit one shot, he hit 51% of his remaining shots. After hitting two shots, he then hit 50% of subsequent shots. The estimated correlation coefficient between the outcome of one shot and the next was a statistically insignificant −0.039, suggesting that shooting streaks are an illusion. Take a look at this YouTube video of Houston Rocket’s star player Tracy McGrady’s amazing performance in the final 35 seconds of a crucial game against the San Antonio Spurs on December 9, 2004, a performance that many basketball fans believe cumulated into the greatest series of plays in National Basketball Association history. If this wasn’t a hot hand, then what was it?
  9. One way to demonstrate the implication of the Law of Small Numbers is to show how small samples are inclined to result in greater extremes in terms of deviations from expected lottery outcomes. To see this, suppose a jar is filled with a total of six marbles—three green and three red. You randomly choose three marbles without replacement. Calculate the probability of choosing the extreme of either three red or three green marbles. Now, assume the jar is filled with a total of eight marbles—four green and four red. You randomly choose four marbles without replacement. Show that the probability of choosing the extreme of either four red or four green marbles is now less than it was when the jar was filled with three green and three red marbles.
  10. Name a bias in this chapter that is likely to occur as a result of having adopted the Affect Heuristic. Name a bias that is a likely result of having adopted the Availability Heuristic.
  11. Logicallyfallacious.com poses two questions. Answer each one. What fallacy are these two questions setting you up to fall victim to? Question 1:  While jogging around the neighborhood, are you more likely to get bitten by someone’s pet dog, or by any member of the canine species? Question 2:  Sarah is a thirty-something-year-old female who drives a mini-van, lives in the suburbs, and wears mom jeans. Is Sarah more likely to be a woman or a mom?
  12. Can you think of a situation in your own life where undertaking a “premortem” would likely help you avoid falling victim to the Planning Fallacy?
  13. In the Bayes Rule example of Stereotyping, how low would the probability that a Hello taxi was involved in the accident given the witness’s testimony (i.e., 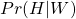Pr(H|W)) have to be in order for the probability of a Hello taxi having been in the accident to equal 15%?
  14. Can you think of an example where “less is more”? Henry David Thoreau, the 19th Century American naturalist, essayist, and philosopher, did so when he wrote in Life in the Woods (a.k.a Walden Pond) that a man’s wealth is determined by the number of things that he can live without.
  15. Think of a way in which you have conformed to a social norm. Describe both the social norm and how you went about conforming to it. In what ways has your conformity both benefitted and harmed you?
  16. When a bank recently stopped charging per transaction (e.g., check fees and fees per phone-banking transaction) and changed to a per-month flat rate, their revenues went up by 15%. What is the most likely cause of this response among the bank’s customers?

Media Attributions

  1. Of course, it can be argued that those who guard more against committing Type 1 error are just as likely to exhibit Confirmation Bias. In my case, this counterfactual situation would have me guarding against blaming my wife. But since our children no longer live under our roof, and we own no pets capable of playing hide and seek with my things, this scenario would require that I blame myself first and foremost. Perish the thought! ↵
  2. The opposite of this law, the Law of Large Numbers, is what underpins the correct answer, “yes,” to this experiment’s question. Interestingly, the law’s application here does not specify a threshold number of births beyond which we would expect to see more of an alternating pattern. Rather, as applied here, the Law of Large Numbers merely implies that six is too small a number. ↵
  3. Clotfelter and Cook (1991) and Terrell (1994) tested for a version of the Law of Small Numbers known as the Gambler’s Fallacy based upon state lottery data from Maryland and New Jersey. In both lotteries, players try to correctly guess a randomly drawn, three-digit winning number. Both studies found that relatively few players bet on a number that had recently won the lottery. Gamblers in the New Jersey lottery who succumbed to this gambler’s fallacy paid more of a price than those who succumbed in the Maryland lottery. This is because in the Maryland lottery all players who pick the correct number win the same prize amount, while in New Jersey a jackpot amount is split evenly among all the winners. Thus, a player in the New Jersey lottery wins more the fewer the number of other winners, in which case picking a number that recently won the New Jersey lottery is actually a better strategy (or less-worse strategy) in New Jersey than it is in Maryland. One would therefore expect to find fewer players succumbing to the Gambler’s Fallacy in New Jersey than in Maryland. Although this did occur, the difference was only slight, suggesting that gamblers are hard-pressed to overcome the fallacy even when it is in their best interest to do so. ↵
  4. In a second experiment, Rothbart et al. test whether group members who are considered most salient have a disproportionate impact on our impressions of the group as a whole, in particular, whether “extreme individuals,” by being novel, infrequent, or especially dramatic, are more available in memory, and thus, overestimated when judging their presence in the group. The authors ran the experiment with extreme instances of physical stimuli (men’s heights) and social stimuli (unlawful behavior). In accord with the authors’ predictions, subjects gave significantly higher estimates of the number of stimulus persons in the groups with extreme conditions—over six feet tall (in the physical stimuli treatment) and criminal acts (in the social stimuli treatment). ↵
  5. For a nice synopsis of the original Asch conformity experiment, along with more recent conformity findings, see McLeod (2018). ↵
  6. Hindsight Bias is a special case of biases associated with “optimistic overconfidence,” of which there are several examples. For instance, Svenson (1981) questioned drivers in the US and Sweden about their overall driving skills. 93% of US drivers and roughly 70% of Swedish drivers believed they drive better than the respective average drivers in their countries, indicating general overconfidence in their driving skills. In some instances, people may express Hindsight Bias in a less egotistical manner by believing that others possess the same level of skill or knowledge as they do. This is what’s come to be known as the “curse of knowledge.” Whereas Hindsight Bias results when Homo sapiens look backward in time, a similar bias results when we look forward in time (i.e., when we predict the future), called Projection Bias. Projection Bias occurs when we do not change how we value options (e.g., decision outcomes) over time. Thus, we tend to ignore the impacts of certain factors that have changed in the intervening time, which can later lead to regret at having made the decision we did. As we will see in Chapters 4 and 5, Hindsight and Projection Biases lead to what’s known as the “time-inconsistency problem” for Homo sapiens, where what we believe we will want at some future time disagrees with what we actually want (and therefore choose) at that future time (which can be thought of as an inter-temporal version of a preference reversal). ↵
  7. Nevertheless, those patients undergoing the extended procedure reported having experienced less pain in the final moments of their procedures than those undergoing the shorter procedure. ↵
  8. In a related study of members of three health clubs in Colorado, Gourville and Sorman (1998) found evidence of what’s known as “payment depreciation,” whereby payment for club membership has a diminishing effect on members’ use of the club as time goes on. Memberships in these clubs were purchased on an annual basis with payments made semi-annually from the time of enrollment. For instance, a member joining in January would pay in January and June each year. The authors found that no matter when the month of payment occurred, there was a substantial spike in attendance immediately following payment. Approximately 35% of the average member’s attendance during any six-month window occurred in the month of payment. In contrast, roughly 10% of attendance occurred during the fourth or fifth month after payment. ↵
  9. The authors also test several hypotheses about why Homo sapiens may choose greater diversity in a simultaneous-choice setting, but not as a result of Diversification Bias. Rather, the reasons stem from mispredictions of taste, risk aversion and uncertain preferences, and information acquisition about a larger variety of commodities. ↵
  10. These biases are measured by Pronin et al. in an objective reality context. Related research conducted by Cheeks et al. (2020) shows that people are similarly susceptible to the Bias Blind Spot in the subjective domain of art appreciation. ↵
  11. In Chapter 5 we will learn how researchers discern differences like these on a more formal, statistical basis. ↵

License

Icon for the Creative Commons Attribution 4.0 International License

A Practicum in Behavioral Economics Copyright © 2022 by Arthur J. Caplan is licensed under a Creative Commons Attribution 4.0 International License, except where otherwise noted.

Share This Book