22 How Do We Know the Laws of Nature Are True?

We should begin by noting that laws of nature are general statements about regularities that objects and their features must obey. Force is always required to cause a mass to change velocity. Pressure is always directly proportional to temperature and inversely proportional to volume. Overall entropy never decreases in an isolated system. Laws of nature are lawlike in the generalities they describe and in their force. They do not invoke specific particular objects, like the phone in your pocket or the top of Mt. Fuji or Larry from down the hall. Laws of nature state general truths which may apply to all relevant particulars but never focus on any specific particulars.

But, of course, all we ever see are specific particulars. And, as noticed back in our discussion of phenomenalism, we see that events happen, but we never see the necessity in their happening. So how do we arrive at knowledge of laws of nature?

One might begin by thinking that we arrive at knowledge of laws of nature by observing a phenomenon repeatedly and seeing what regularities hold. So, for example, a line of frogs comes our way, and the first one hops, and the second one hops, and the third one hops, and so on, and eventually we begin to think that maybe “all frogs hop” is true. That is a general statement, and it seems to be based on observing a string of particulars.

But there is a logical problem. It simply does not follow from the claim that one frog hops and a second frog hops and a third one hops that all frogs hop. Moreover, the observation that all the frogs observed so far hop does not demonstrate any necessity in their hopping. Consider for contrast the situation in which an old man in front of you in line at a convenience store pulls one penny out of his pocket and then pulls another one out of his pocket and then a third one… As frustrating as the experience may be for you, you should not conclude from it that all coins in the pockets of old men in convenience stores must be pennies. Your tedious experience does not allow you to boast that you have discovered a new law of nature.

Of course, doing real science is harder than just watching frogs hop or old men count out change. Scientists observe carefully, employ control groups, and run tests to find accidental correlations. But even so the logical fact remains that no number of particular observations show the truth of a general and necessary claim. Put another way, a general truth, like a law of nature, is always underdetermined by its evidence. This, by the way, is known as the problem of induction, and it was made famous (or infamous) by David Hume (1711-1776). To make the point in another way, suppose we make five careful observations. Which of the dotted lines most accurately portrays the law of nature we have discovered?

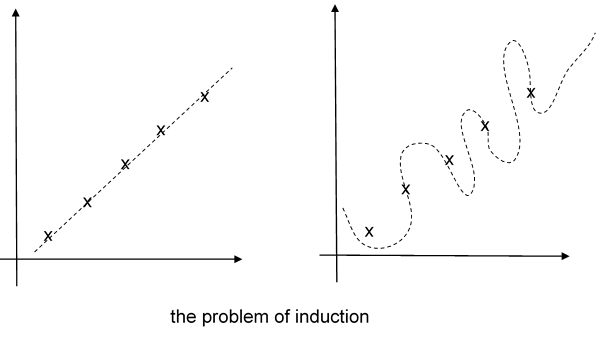
They both do; each one models our data. The problem though is that there just isn’t enough data to tell us what to do with the spaces in-between the data points. This is what is meant by “under-determination.” The two different ways of construing what is going on make different predictions about what patterns we will find as we make further observations. Further observations may help us to rule out some possibilities. But no matter how many further observations we make, we will always have many different ways of connecting the dots.

So we do not easily “read off” general statements from the data. What do we do? At this point it would be sensible to admit that our observations of particulars do not demonstrate what the laws of nature are. Instead, perhaps they only give us some idea of what sorts of correlations there might be in the world, and based upon this idea we frame a hypothesis about what the laws of nature are. The hypothesis, we will admit, may be true or false, but it is a good guess based on what we have seen so far.

This suggestion obviously brings us to the famed scientific method. The method, in short summary, is this. Begin with some observations; frame a hypothesis; generate a prediction from the hypothesis; devise a test to determine if your prediction is accurate; if it is – well done, keep testing; if it isn’t – then start over. We need not go into further detail for our purposes, and the method is probably already familiar to most readers.

Note, however, that the scientific method does not deliver certain knowledge of the laws of nature. Each known law of nature is a hypothesis that has not yet been decisively refuted by experiments. That is the most that can be said of the hypothesis, and it is clearly not the same as saying that some law of nature is known with certainty. But perhaps that is okay. As we have seen, knowledge need not be certain in order to count as knowledge; it need only be a justified, true belief (recall JTB) whose truth helps to explain why it is believed (JTB+). So long as we are justified in our belief of the scientific claim that has been made (which we have not yet discussed), then it will turn out that we know the claim – just so long as it does turn out to be true, and the JTB+ conditions have been met.

This gives us occasion to reflect on the sentence “It’s only a theory.” Many times people use this phrase to remind us that the theory of evolution, for instance, is only a theory. It is implied that when something is only a theory, it is not known with certainty, or perhaps not even known very well at all. But once we recognize that very little of our knowledge of nature is known with certainty, we should reject the implication behind saying “It’s only a theory.” If “theory” just means not known with certainty, then basically all of the knowledge of nature we use to build bridges, cure diseases, manufacture cell phones, and boil water is only a theory. And in fact, this is not a good way to understand the term “theory” anyway. A common definition of the term is that a theory is “a supposition or a system of ideas intended to explain something, especially a system based on general principles independent of the thing to be explained.” Note that nothing is said about certainty. A theory is an explanation-provider; whether any particular theory is plausible or not, or very likely true or not, or even certain or not, is a completely separate matter.

This admission, that we can never know with complete certainty whether our claims about the natural world are true, is called fallibilism. Our knowledge is fallible, which means it might turn out not to be knowledge at all. It is a good guess we are working with until we have evidence that it is false.