46 Further Reading
As mentioned, Bayes’ Theorem is usually presented as a formula. The basic question is, “What is the probability of {some event} given this evidence?” The idea is to make the probability proportional to both the probability of the event on its own and the probability that the evidence would exist if the event happened and to make the probability inversely proportional to the probability of the evidence existing, even if the event didn’t happen. So, we have this:

Or, letting A = the event, B = the evidence, and “P(A|B)” meaning “the probability of A given B”, we have:
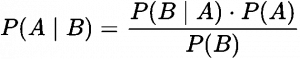
There are many excellent videos about Bayes’ Theorem on YouTube. One that is exceptionally clear is from 3blue1brown, “The medical test paradox: Can redesigning Bayes rule help?”, https://youtu.be/lG4VkPoG3ko.
A fascinating book about the powerful effects of Bayes’ Theorem is Sharon Bertsch McGrayne’s The Theory That Would Not Die: How Bayes’ Rule Cracked the Enigma Code, Hunted Down Russian Submarines & Emerged Triumphant from Two Centuries of Controversy (Yale UP, 2011)
Hume, David. An Enquiry Concerning Human Understanding. Indianapolis: Hackett, 1993. Hume’s argument against believing reports of miracles is chapter 10 of his Enquiry Concerning Human Understanding. It is a classic!
Media Attributions
- Bayes Formula © Charlie Huenemann is licensed under a CC BY-SA (Attribution ShareAlike) license
- Figure 10.2 © Charlie Huenemann is licensed under a CC BY-SA (Attribution ShareAlike) license

