College of Science
82 Development of New Tools for the Study of Superconductivity at Extreme Conditions of Temperature and Pressure
Mason Burden; Audrey Glende; Willis Holle; Julia St. Andre; Jason Chang; and Shanti Deemyad
Faculty Mentor: Shanti Deemyad (Physics & Astronomy, University of Utah)
Introduction
Superconductors are materials with the unique properties of zero DC electrical resistance and perfect diamagnetism. However, the operating conditions of superconductors are currently limited to either very low temperatures or high pressures – conditions which obscure their wider application. The holy grail of condensed matter physics and material science is a superconductor that operates in ambient conditions. The realization of such a material would be revolutionary. Although we know of many superconducting materials, we do not have a universal theory for how they operate. To develop a theory of superconductivity, one path is to construct a form of dimensional phase space from known samples by analyzing their pressures, temperatures, currents, and unit cell parameters at the point they become superconductive. In doing so, we lay out a path to discovering novel materials to harness phenomena in increasingly ideal environments.
The goal of this research is to provide a comprehensive metric to analyze properties of superconductors, which allows for reliable measurements and helps develop and test for a universal theoretical model of superconductivity. One of the most important metrics modernly used to develop this understanding has been the modulation of a sample’s pressure. Unfortunately, the apparatuses required for applying such immense pressure are bulky and consequently bring their own complications. To achieve the required pressures for some superconductive samples, a Diamond Anvil Cell (DAC) is used. This device takes advantage of the roughly inverse relationship between area and pressure by placing the sample between the tips of two diamonds of low area to maximize pressure.
The problem arises when trying to take useful measurements while applying pressure. The DAC physically surrounds the sample and interferes with any mechanical interface used to operate with the sample. Common forms of measurement of superconducting properties such as Scanning Tunneling Microscope (STM) or Angle-resolved photoemission spectroscopy (ARPES) become impossible as they require physical interaction with the sample to be of use. Other techniques can be used – such as DC Four-Probe measurements and AC Magnetic Susceptibility – but they require very precise electronic circuits to be built in or around the DAC. Though these measurements are useful, they can be enhanced using complimentary measurements.
Fortunately, while diamonds are the hardest naturally occurring material, they also happen to have the immensely useful property of being completely transparent to light in and around the visible spectrum. The table of the diamond operates as an optical window pointing directly through the heart of the diamond anvil and onto the sample, even under immense pressure. Through this window, a plethora of optical measurements can be taken. For this work, Raman spectroscopy will be of greatest emphasis.
Raman spectroscopy can be used to measure the superconductive gap. This gap is essentially the energy disparity between electrons and cooper pairs [1]. At the critical temperature of superconductivity (TC), it becomes energetically favorable to form Cooper pairs as the energy gap is zero. Below TC, the energy gap increases in favor of Cooper pairs [1]. This gap can be measured using electronic Raman spectroscopy [3], providing useful insights into superconductive samples.
Raman spectroscopy is a form of optical measurement used to analyze the low frequency vibrational mechanical or electrical oscillations of a system. This is done by firing a laser of a set frequency and measuring the offset of the wavelength of the light scattered from the sample. Three signature frequencies of light will be scattered from the sample, namely the Rayleigh scattering, Stokes Raman scattering, and anti-Stokes Raman Scattering [2]. Rayleigh scattering is simply the light of the same wavelength of our laser. Useful information is stored in the energies of the two other forms of scattering, but they occur at a far lower rate than that of Rayleigh scattering; an occurrence which makes readings much more difficult to achieve. Thus, the apparatus for measuring Raman must be of great precision to absorb enough light to make significant measurements. It is notable that for superconductors the anti-stokes scattering will not occur.
For most Raman setups, this is accomplished by designing systems with extremely short working distances (the distance the focal plane sits away from the last lens). Doing so increases the numerical aperture (the maximal angle a system will accept light from) which increases the percent of light available for collection. This short working distance does not integrate well with DACs, as the sample lies outside the working distance of most Raman spectroscopy systems. Incorporate the massive cryostat structure required for low temperature measurements, and conventional Raman becomes near impossible.
Methods
To address the current sizable disparities in working distance and the distance required by our removed focal plane. We spent time using parabolic mirrors as a solution, but encountered issues with alignment, so we devised n alternative solution. This work proposes a secondary lensing system to extend the working distance of the primary instruments. This solution unfortunately decreases the numerical aperture and proportionally the light received by the sample. To accommodate the extended working distance, a higher-powered laser and a bandpass filter of finer precision can theoretically be used to increase Stokes and Anti-Stokes scattering counts.
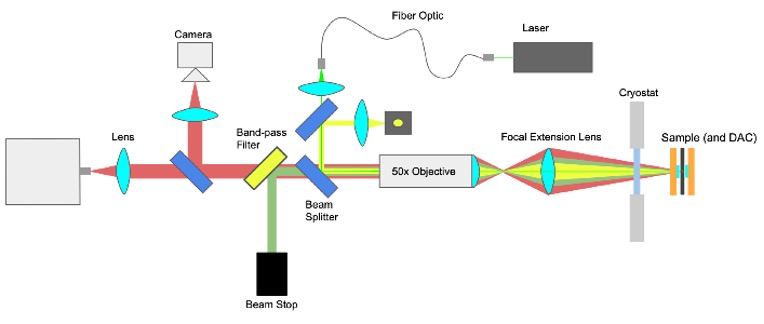
Figure 1. A model of a standard Raman system with modifications to allow for long-distance spectroscopy.
The “Focal Extension Lens” in Fig. 1 is the central focus of this project. By aligning the focus of the extension lens between the focal length of the fifty times objective and twice that same distance we can extend the working distance of our lens. Through careful alignment and construction, long distance microscopy can be realized. This level of clarity can be observed in figures 2 and 3 below.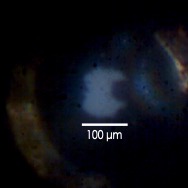
Figure 2. Image of a DAC loaded with ruby sample, taken with a working distance of around three inches.
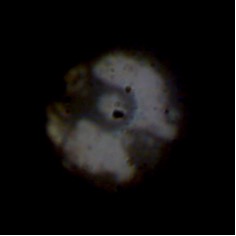Figure 3. Image of a DAC loaded with a CeO2 sample, taken with a working distance of around three inches.
Figure 4. Image of the Raman system in an earlier prototype phase, taking an image of a DAC.
A preliminary test of the system’s effectiveness and alignment was taken using the DAC featured in Fig. 2. A fluorescence reading was used for visual calibration and alignment, the results of which can be seen in Fig. 5.
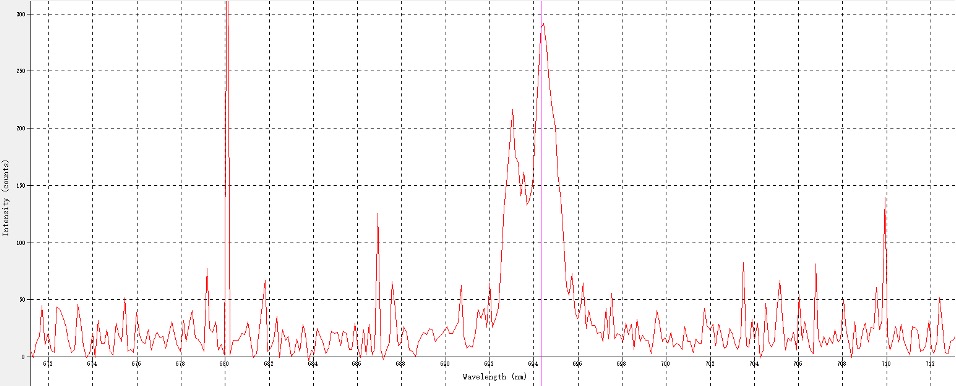Figure 5. R1 and R2 peaks of ruby fluorescence in the Fig. 2 DAC
Conclusion
The results of this work reveal that the extension of the working distance of Raman Spectrometry using a secondary lensing system stand as a viable solution to the limitations of high-pressure low temperature experimentation. While continued work can be done to improve beyond this modification, it appears to already show great promise in terms of imagery and fluorescence. With further effort, it is reasonable to assume that long distance Raman measurements can be achieved and even applied in situations beyond the realm of low temperature high temperature measurements once thought impossible.
Acknowledgements
This work was supported by SPUR from the Office of Undergraduate Research at the University of Utah awarded to Mason Burden. The experimental research at University of Utah was supported by National Science Foundation Division of Materials Research Awards No. 2132692.
References
[1] Cooper, Leon N, “Bound electron pairs in a degenerate Fermi gas”. Physical Review, vol. 104, no. 4, 1956.
[2] A. Lyon et al., “Raman spectroscopy,” Anal. Chem., vol. 70, no. 12, pp. 341–362, 1998.
[3] P. Devereau and D. Einzel, Physical Review, vol. 51, 1995.
