Action Potential Propagation
Jim Hutchins
Objective 10: Describe the process by which action potentials move from the proximal axon to the axon terminal.
Action potentials are carried only on nerve cell axons. This is because only nerve cell axons have the machinery (yellow shading) to propagate (pass and regenerate) an action potential.
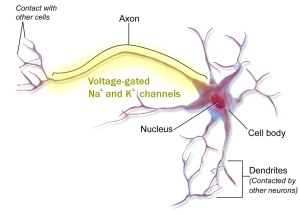
To understand this process, we first need to know (just a little bit) about how current flows in a wire.
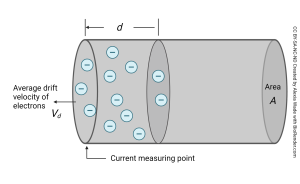
Electrons drift with a bias towards moving one direction, and this creates an electromagnetic wave. This moving electromagnetic wave spreads at near-light speed through the wire, carrying current as it goes. (For this discussion, we’ll consider current — the number of electrons passing by a single point per second, like a river current — as interchangeable with voltage, the difference in the number of electrons in the river vs. on the riverbank.)
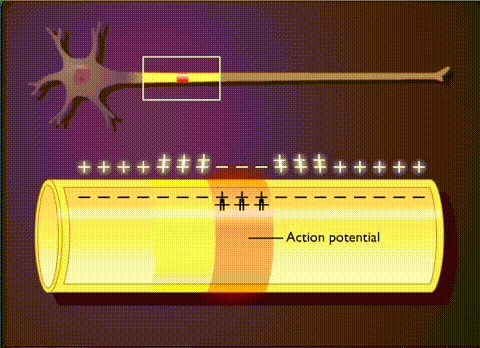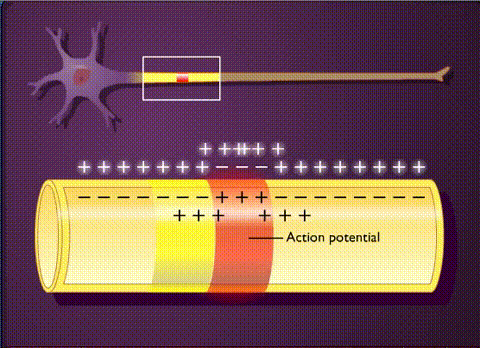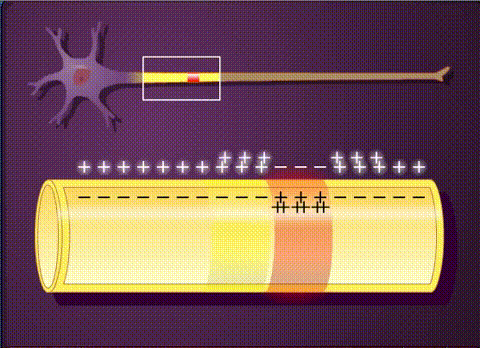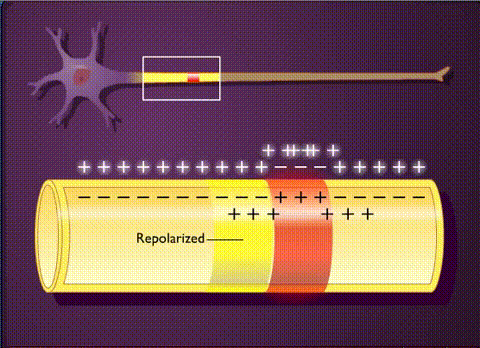
Another way of looking at this in in the animation shown here, illustrating the spread of positive charges (mostly potassium ions) in a nerve axon.
Current and voltage spread from a single point is shown by this graph. Note that the shape of the two curves is the same, but the purple curve, showing a large myelinated axon, loses its peak voltage much slower than the black curve, showing a small unmyelinated axon.
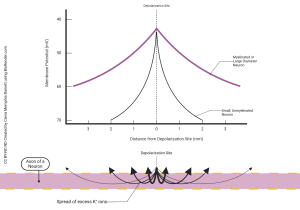
Start at the channel where positive ions flow in (“depolarization site”). Ion flow is an electrical current, and the electrical current (ion flow) is at a peak where the ions come in. This causes a peak change in membrane voltage, making it more positive.
Then, as we move further from the point where the ions enter, they spread out in both directions, getting diluted as they go, so the voltage change is smaller and smaller the further we get from the point where it entered.
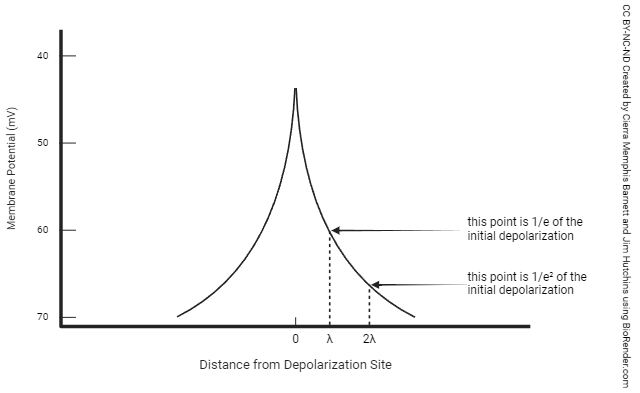
The term of art we use to describe this slow, steady decline from a peak is decrement. Current, or voltage, injected at a single point along the neuronal membrane will decrement over distance as we travel further away from the point of injection.
Current, or voltage, injected at a single point along the neuronal membrane will decrement over time as we observe that single point over a period of several milliseconds.
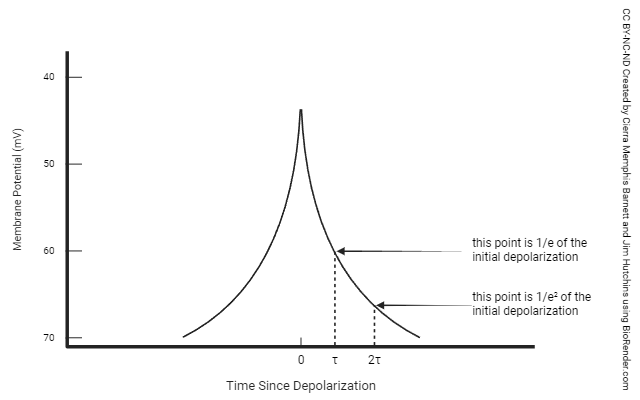
You don’t need to know this unless you become a neuroscientist, but the distance it takes for voltage to drop to 1/2.71828 of its initial value is called the length constant (λ).
The time it takes for voltage to drop to 1/2.71828 of its initial value is called the time constant (τ).
Why such a weird number (1/2.71828)? Mathematicians have some numbers that have special properties, and the number 2.71828··· is one of those. It’s called e or Euler’s constant. Like pi (π) it shows up in a lot of weird places, and like π it goes on forever. For example, e shows up in the calculation of the equilibrium potential. Remember that the equilibrium potential was something we discussed earlier but we didn’t get into the detailed mathematics explaining it. There’s a good reason for that.
The length constant and time constant are useful to understand the idea of graded potentials and summation which we will discuss in Objective 10.
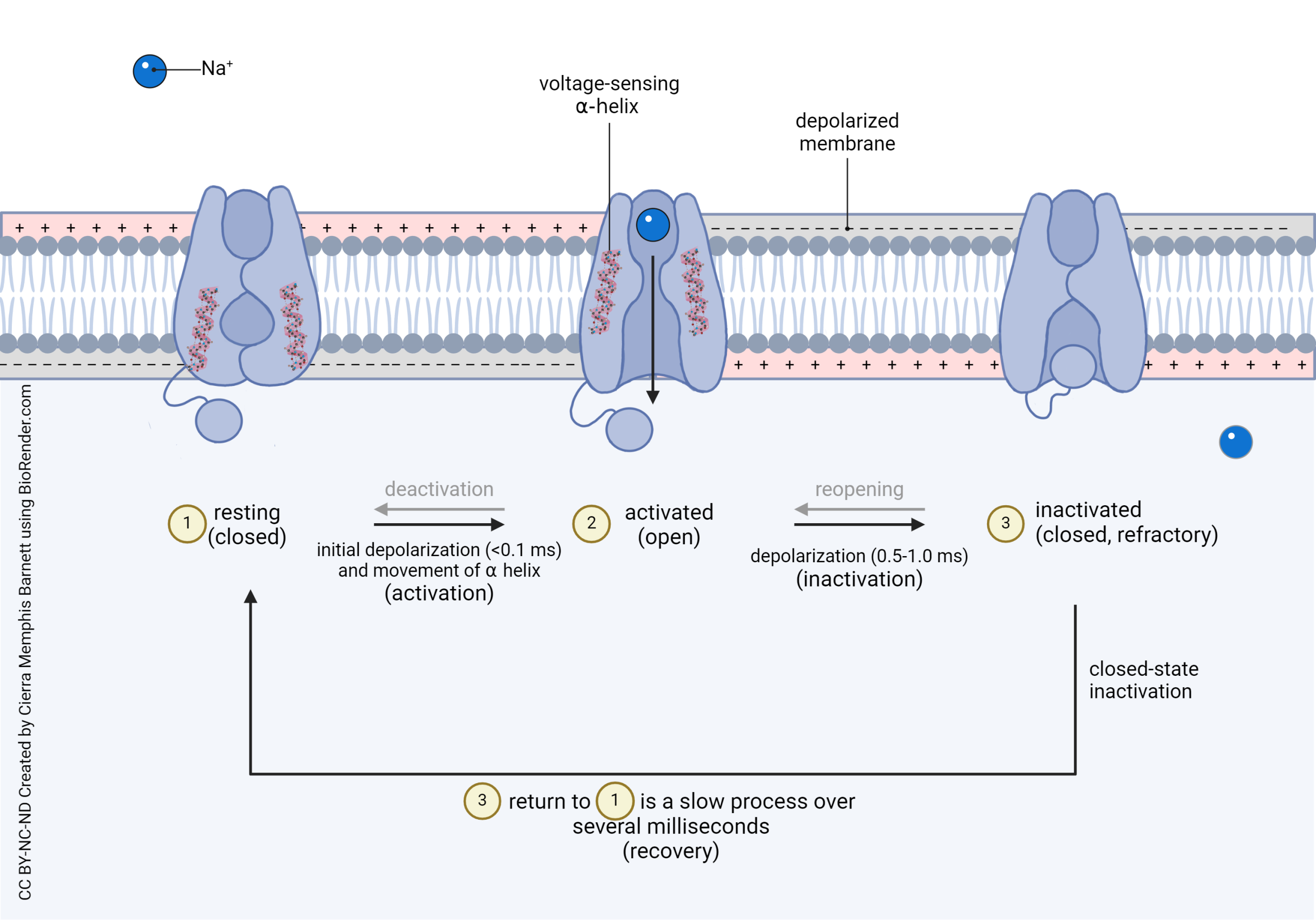
This is the representation of the voltage-gated Na+ channel we saw earlier. Remember that the voltage-gated Na+ channel has three states. The third state, starting at about 1 msec after its activation, is the closing of the inactivation gate, represented by the ball-and-chain.
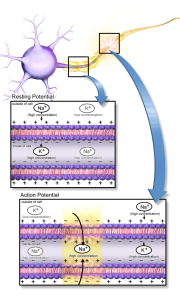
The action potential is generated at a decision point for the neuron, the axon hillock or initial segment. This is where the cell body (left) and axon (right) meet. In this diagram, the cell body membrane to the left of the initial segment has neither voltage-gated Na+ channels nor voltage-gated K+ channels, so no action potentials can be generated in that part of the neuron.
The axon membrane to the right of the initial segment does have voltage-gated Na+ channels and voltage-gated K+ channels. It can support an action potential. So a small segment of the axon, just to the right of the initial segment in this diagram, fires an action potential.
Now we’ll shift our focus slightly. In the middle of this axon, the patch of axonal membrane to the left of the action patch has just been through an action potential .The voltage-gated Na+ channels there are refractory (inactivated). They did the action potential “thing” a couple of milliseconds ago, and they’re over it. Their inactivation gates are closed, and they cannot be reopened until the voltage-gated Na+ channel resets (i.e. returns to the resting state, which takes several milliseconds).
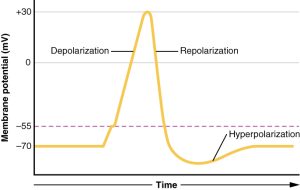
Remember that the falling phase of the action potential is due to two overlapping events:
- sodium channels inactivate, which prevents the entry of these positive ions;
- potassium channels open, and this allows positive ions to leave the neuron, making it more negative inside.
We will focus on the sodium channel inactivation, because these inactivated sodium channels keep the action potential moving in the same direction.
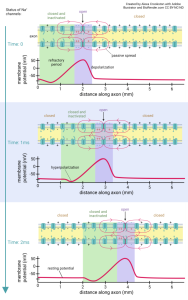
Note that the horizontal axis is distance along the axon, not time. That’s why this curve does not exactly match the action potential voltage trace.
This is just another representation of the same idea. The green shaded part of the axon is refractory (inactivated). The purple part is going through an action potential. The yellow part is ready for a new action potential. Notice the yellow shading returning to the left side of the axon as the action potential moves to the right from top to bottom in the diagram.
Media Attributions
- Voltage gated Na K channel distribution © BruceBlaus adapted by Jim Hutchins is licensed under a CC BY (Attribution) license
- Electrons in a Wire © Alexia Wade is licensed under a CC BY-NC-ND (Attribution NonCommercial NoDerivatives) license
- Action potential propagation in unmyelinated axon © Germis is licensed under a CC BY-SA (Attribution ShareAlike) license
- Membrane Potential and Depolarization © Cierra Memphis Barnett is licensed under a CC BY-NC-ND (Attribution NonCommercial NoDerivatives) license
- Length Constant © Cierra Memphis Barnett and Jim Hutchins is licensed under a CC BY-NC-ND (Attribution NonCommercial NoDerivatives) license
- Time Constant © Cierra Memphis Barnett and Jim Hutchins is licensed under a CC BY-NC-ND (Attribution NonCommercial NoDerivatives) license
- Voltage Gated Sodium Channel Internal Gate Mechanisms Membrane Charges © Cierra Memphis Barnett is licensed under a CC BY-NC-ND (Attribution NonCommercial NoDerivatives) license
- Action Potential Nerve © BruceBlaus is licensed under a CC BY (Attribution) license
- Action potential © Betts, J. Gordon; Young, Kelly A.; Wise, James A.; Johnson, Eddie; Poe, Brandon; Kruse, Dean H. Korol, Oksana; Johnson, Jody E.; Womble, Mark & DeSaix, Peter is licensed under a CC BY (Attribution) license
- Sodium axon action potential graph © Alexa Crookston is licensed under a CC BY-NC-ND (Attribution NonCommercial NoDerivatives) license

