Pre-Service Elementary School Teachers’ Perception of Themselves as Learners of Mathematics and Science
Diana L. Moss, Ph.D.; Rachel Wilson, Ph.D.; and Danielle Divis
Abstract
This study investigated how prospective elementary teachers view themselves as learners of mathematics and science during their last year in a teacher preparation program at an American university. Using drawing and reflections as the method for collecting data, prospective teachers were prompted to draw themselves and reflect on learning mathematics and draw themselves and reflect on learning science prior to and after their mathematics and science methods courses. Drawings (n = 147) were coded according to the presence or absence of several themes including physical objects, teachers, students, and environment. The drawings and reflections indicated that the experience of participating in mathematics and science methods courses taught from a social constructivist perspective positively impacted prospective teachers’ conceptions of themselves as learners and in ways consistent with current research-based pedagogies. The research study described here proposes that prospective teachers’ learning experiences in mathematics and science methods classes might impact how they will teach mathematics and science in their future elementary classrooms.
Keywords: prospective elementary teachers, mathematics education, science education, pre-service teacher identity
Pre-service elementary teachers (PSETs) enter their methods courses with beliefs about learning mathematics and science based on prior education and life experiences (Hsu, Reis, & Monarrez, 2017). These beliefs can affect how pre-service teachers view themselves as learners as well as how they navigate the process of becoming a teacher (Lortie, 1975). The becoming a teacher process is influenced by the “experience of schools and teaching that [PSETs] bring with them to teacher preparation courses” (Beltman et al., 2015). Teacher educators are challenged to navigate PSETs’ beliefs and prior experiences to prepare them to become effective classroom teachers.
Using drawings and written descriptions, this study investigated how PSETs view themselves as learners of mathematics and science during their last year in a teacher preparation program. Specifically, how do PSETs’ perspectives on learning change after taking methods courses in mathematics and science?
Literature Review
Social Constructivism Learning and Environment
The constructivist learning theory supports teaching mathematics and science through inquiry where learning is student-centered, rather than lecture-based (Fosnot, 1996). A shared intention in mathematics and science teacher education is to prepare PSETs to teach from a social constructivist (Vygotsky, 1978) perspective (National Research Council [NRC], 2007). In the theory of social constructivism, the central tenet is that learners construct their own understanding by participating in meaningful shared discourse. Although Vygotsky (1978) used speech as the primary mediation tool upon which to focus his studies, he noted other mediation tools such as symbols, algebraic systems, art, drawing, writing, and diagrams (Brooks, 2009). Brooks (2009) theorizes that “drawing might contribute to the formulation of thinking and meaning” (p. 2).
Further, learners are limited in what they can learn independently, and more can be learned with assistance from teachers and collaboration with others (Carlile & Jordan, 2005). In an environment conducive to learning mathematics and science, the teacher plays a vital role. The teacher not only needs to use interesting and engaging problems, but also encourage discussion and provide representations of multiple methods, support conceptual understanding, and encourage critical thinking (Davis et al., 2006; Picone-Zocchia & Martin-Kniep, 2008). Social constructivism accounts for the interactive communications that occur between teaching and learning, where teachers and students are “active meaning makers who continually give contextually based meanings to each other’s words and actions as they interact” (Cobb, 1988, p. 88). Moreover, the NRC (2001) contended that students must develop a “productive disposition” toward mathematics and believe that they are capable of learning and using mathematics (p. 131). Teachers that have a productive disposition are confident doers of mathematics and science who? encourage and support their students. Students who are learning in a positive environment should feel comfortable expressing their learning approaches and engaging in problem solving. Moreover, the teaching of mathematics and science should not focus entirely on the content but should consider the interactions that occur between teachers, students, and content as well (Cohen & Ball, 1999; Davis et al., 2006; Windschitl, 1999). These valuable interactions set the stage for productive thinking and learning.
Teacher Professional Identity Construction
A common challenge in both mathematics and science education is developing new teachers’ professional identities in line with research regarding mathematics and science thinking, teaching, and learning. Lave and Wenger (1991) and Wenger (1999) approached identity research from a sociocultural perspective where they framed? identity as dynamic (being reformed over time based on experience and personal meaning-making) and formed in communities with social and historical influences. In this perspective, identity links? to learning because “learning is conceptualized as the process of becoming a certain kind of person in relation to mathematical activity” (Langer-Osuna & Esmonde, 2017, p. 637). Researchers have suggested that new teachers tend to teach mathematics and science the way that they have been taught (Avraamidou, 2014a; Clift & Brady, 2005; Eick & Reed, 2002; NCTM, 2014; Zeichner & Tabachnick, 1981). Moreover, Avraamidou (2014b) and Luehmann (2007) have argued that by examining the identity work of teachers, we, teacher educators, can examine teacher learning and the factors that affect the development of teacher identity related to teaching science. By using an identity framework in research with pre-service and beginning teachers, researchers recognize that content-specific learning experiences within teacher education programs and in their previous schooling impact teacher beliefs about and emotions related to teaching that content (Wilson & Kittleson, 2012; Carrier et al., 2017; Timoštšuk & Ugaste, 2010).
PSETs’ Epistemological Beliefs
PSETs’ professional identity embodies and is embodied by their epistemological beliefs. Although content impacts learning in mathematics and science, the experiences that occur in the classroom also shape and influence the learning that takes place (NCTM, 2014; NRC, 2012). These experiences that occur in teacher education courses play an essential role in integrating beliefs and theory (Huang et al., 2021). For instance, negative experiences in mathematics classrooms influence PSETs’ perceptions of the subject, and sometimes cause negative feelings or anxiety toward learning and teaching mathematics. Mathematics anxiety is persistent among pre-service teachers (Bekdemir, 2010; Gresham, 2007; Hembree, 1990). Bekdemir’s (2010) study found that PSETs’ negative experiences in learning mathematics not only cause anxiety towards mathematics, but the anxiety towards mathematics increases as the grade levels progress. Studies have also found that anxiety towards mathematics is caused by teachers’ behaviors and approaches to teaching mathematics (Andrew, 2004; Bekdemir, 2010; Frank, 1990; Hadfield & McNeil, 1994; Harper & Daane, 1998; Hembree, 1990; Jackson & Leffingwell, 1999; Perry, 2004). These prior mathematics experiences influence PSETs’ beliefs about learning in their methods courses. Thus, a cycle of mathematics anxiety is present where the educators’ anxiety impacts the students’ anxiety (Vinson, 2001). This occurs because anxiety can impact teachers’ abilities to teach mathematics with confidence (Akerson, 2017). Further, teachers cannot be expected to generate enthusiasm and excitement for a subject for which they have fear and anxiety. If the cycle of math phobia is to be broken, it must be broken in the teacher education institution (Mihalko, 1978, p. 36).
Studies have found that PSETs’ prior learning experiences in science influence their beliefs toward the subject content, their ability to learn the subject, and their views about how to teach it to students (Carrier et al, 2017; Cavallo et al., 2002; Hsu et al., 2017; Kazempour, 2008, 2013). When PSETs describe their beliefs towards science learning as negative or neutral, these beliefs are associated with experiences of learning science through passive means, including lectures, worksheets, textbooks, and/or lack of collaborative learning (Hsu et al, 2017; Kazempour, 2008; Mensah, 2011). These negative beliefs, as a result of their own learning experiences, have been linked by researchers as influences on PSETs’ beginning teaching identities (Carrier et al., 2017), their ideas about how to teach science (Hsu et al., 2017), and how often they are willing to teach science (Cavallo et al., 2002). When methods courses include an element of reflection for PSETs about their prior learning experiences in science, along with models of inquiry-based teaching and collaborative learning, PSETs with previously negative learning experiences were able to make significant improvements in their beliefs toward the subject (Kazempour, 2008) and include research-based practices as a part of their beginning teaching identity (Mensah, 2011).
Therefore, our study seeks to determine how PSETs’ learning experiences in their mathematics and science methods courses impact their perceptions of learning mathematics and science, and in turn, how this might influence how they teach mathematics and science to their future students.
Theoretical Framework
Narrative Identity
Narrative identities are stories from students and teachers that help them make sense of their learning experiences. Sfard and Prusak (2005) argue that identities are a “collection of stories told about persons” and that these stories are influenced by participation in different contexts. However, narrative identity can focus on “stories told about the self” (Langer-Osuna, 2017) and complements positioning theories where participation in social practices is linked to individual formation of identities (Lave & Wenger, 1991). Sfard and Prusak’s (2005) definition of narrative identities differs from Wenger’s (1999) theory in that Wenger focused on experiences rather than stories. For example, research (Bartholomew et al., 2011; Rodd & Bartholomew, 2006; Solomon, 2007) indicated that “students’ stories about mathematics tend to focus on how they develop a sense of belonging or exclusion” (Langer-Osuna, 2017). Teachers’ narrative identities demonstrate how their own learning experiences relate to their approaches to teaching mathematics and science (Adams, 2013; Mensah, 2011; Rivera Maulucci, 2013; Williams, 2011). It is unclear from the research if and how teacher and student identities relate to each other (Langer-Osuna, 2017). Narrative approaches to studying identity can provide a lens into how PSETs envision themselves as teachers of mathematics and science. We propose that drawing used in conjunction with written explanation can be a narrative approach that serves to analyze the stories of many individuals, “enabling analysis of patterns of experiences and stories” (Langer-Osuna & Esmonde, 2017, p. 641). PSETs’ drawings in mathematics and science methods courses can be used to study their identities and beliefs about learning mathematics and science.
Drawings are most often used in the elementary setting to observe children’s thoughts and emotions towards different content areas. Limited research exists on using drawings to explore the images and experiences that pre-service teachers associate with mathematics (Burton, 2012; Lee & Zeppelin, 2014; Rule & Harrell, 2006). Research has explored the drawings of PSETs and their perspectives on science teaching (Katz et al., 2010; Mensah, 2011; Mensah & Fleshman, 2017), but not necessarily as a way to document the science learning experiences of PSETs. Others (Akerson, 2017; Burton, 2012) have used drawings to investigate pre-service teachers’ internship experiences. Drawings have also been used as a form of narrative writing for second- and third-grade students (Caldwell & Moore, 1991) and can be particularly useful in regulating emotions (Drake & Winner, 2013). Rule and Harrell (2006) recommend that drawings be included in mathematics methods courses to connect pre-service teachers to their unconscious images of mathematics and to help shift their emotions towards mathematics to a more positive mindset.
A Framework for the Scholarship of Teaching and Learning
PSETs’ drawings completed before and after methods courses can be used as evidence of student learning to ensure that the learning goal of the methods courses are being met. In the scholarship of teaching and learning, student learning should be based on the teacher’s teaching philosophy (Stipek et al., 2001). The following figure offers a model that connects our (Teacher Educators’) teaching philosophy with the learning goal for PSETs, teaching activity for PSETs in methods courses, and evidence of PSETs’ learning.
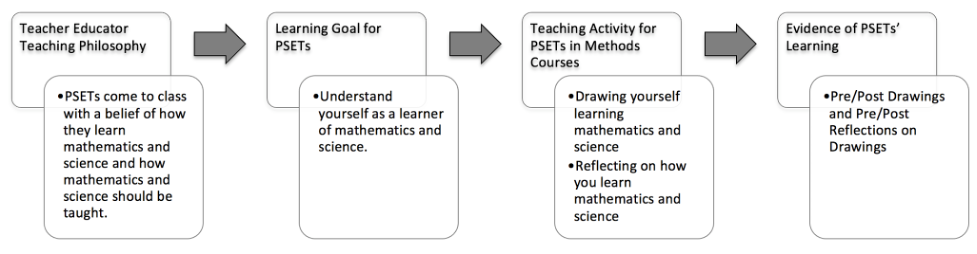
A major learning goal in our methods courses is for PSETs to understand themselves as learners of mathematics and science. This means that we want the PSETs to reflect on how they learned mathematics and science in their pasts and compare and contrast these teaching approaches to instructional practices that they hope to develop. We encourage them to revise and challenge their assumptions about learning and teaching mathematics and science. Based on this framework, this study aims to examine PSETs’ perceptions of themselves as learners of mathematics and science by analyzing PSETs’ stories through pre- and post-drawings as well as descriptions of their drawings.
Methods
Context
The context for the study was an undergraduate elementary education program at a regional comprehensive master’s university in the southeastern United States. We, a mathematics teacher educator and a science teacher educator, each were teaching a methods course in the program: a) the first of two mathematics methods courses taken in the third year of the program, and b) the only science methods course taken in the fourth year of the program. The program, and the College, have social constructivism as a core philosophy. Therefore, classes are structured where teacher candidates participate as “students” in model activities, develop their pedagogical content knowledge, and analyze, deconstruct, and discuss activities in light of pedagogical strategies and content topics (Luehmann, 2007). This course structure is meant to address the possible scenario that PSETs might not have experienced such social constructivist learning environments and to encourage their confidence within this philosophy of teaching and learning. A course goal that is central to both the mathematics and the science methods courses is for PSETs to reflect on how they learned mathematics and science in their prior school experiences. We encourage them to compare and contrast the kinds of instructions that they experienced to the approaches to teaching in our methods courses. Thus, learning to pay attention to their own learning experiences will help PSETs articulate, challenge, and revise their assumptions about teaching and learning mathematics and science.
We exposed PSETs to discipline-specific practices (e.g., science: scientific and engineering practices and science process skills; math: e.g., the standards for mathematical practices (CCSSM, 2010). Additionally, in facilitating model activities for PSETs to highlight research-based pedagogical strategies, we use general and discipline-specific materials while students work in cooperative-learning groups. In both courses, students complete a field experience internship in a local public school. In the mathematics methods course, PSETs complete the internship at the end of the course and are responsible for conducting a diagnostic interview with three students. The purpose of the diagnostic interview is to assess what the students know and can do rather than report what they cannot do. In the science course, PSETs are responsible for creating and implementing a 3-day 5E unit in their internship classroom. In this internship experience, PSETs have a chance to teach using strategies they experienced as students in the science methods course and to see how elementary students respond to such teaching practices.
Participants
Participants in the study are all elementary education majors, therefore, they are all pre-service elementary teachers (PSETs). At the time of data collection, PSETs enrolled in each of the teacher educators’ courses were asked by an outside visitor if their drawings and written descriptions from two class activities during the semester could be collected for research. The outside instructor kept the signed consent forms in their office until the end of the semester. In this way, the instructors did not know who had agreed to participate until after final grades were turned in. Seventy-two students from three sections of the mathematics methods course consented to participate, while 75 students from four sections of the science methods course consented to participate.
Data Colleciton
On the first day of class, PSETs were given the first prompt: “Draw yourself learning math” or “Draw yourself learning science” and asked to “Explain your drawing below” in written text. This style of prompt is similar to that used in other studies investigating PSETs identities related to science teaching (Katz et al., 2010). On the last day of class, students were asked to repeat the prompt. They did not have their initial response available to them when they completed their final prompt.
Data Analysis
Drawings and written descriptions were collected from all PSETs enrolled in the mathematics and science methods courses. At the end of the semester, only those PSETs that provided consent for their classwork to be used for research were used in the data analysis. First, the student work was de-identified and labeled with numbers to keep track of matching initial and final course drawings and written descriptions and to keep PSETs’ participation confidential. All names used in the findings section (below) are pseudonyms. We chose a subset of science (n = 16) and mathematics (n = 16) drawings and written descriptions to develop emergent codes and categories (Charmaz, 2008). Though we allowed the codes and categories to emerge from the data, as teacher educators, we focused on labeling ideas within the drawings with words or phrases that are pertinent to evidence-based teaching strategies. For example, when students included pencils and paper in their drawings, instead of labeling them individually, we coded them as generic classroom materials, whereas when students included math manipulatives or hand lenses, we coded these as materials for hands-on learning. Emergent codes and categories for each set of drawings were compared across content courses and a shared coding scheme for drawings and written descriptions was developed. All initial science and mathematics drawings and written descriptions were then coded with the shared coding scheme. Elements in drawing and writing were coded as present (1) or absent (0). Results for each PSETs’ initial and final work were recorded in a spreadsheet, which was then exported to SPSS for analysis to compare the results of the presence/absence of elements in the initial vs. final drawings and written descriptions. Once in SPSS, we performed a McNemar test (Siegal & Castellan, 1988), assuming course activities are a “treatment,” to determine if there were significant changes across PSETs’ work between their initial and final drawings and written descriptions. All codes for the drawings are included in Appendix A and all codes for the written descriptions are included in Appendix B. The codes that showed significance, p < .05, for both mathematics and science drawings and written descriptions are reported and discussed in the following section.
Findings
Drawing Results
Analysis of the pre/post mathematics and science drawings data resulted in a significant difference, p < .05, in the proportion of eight categories in pre- and post- methods courses. Table 1 indicates the categories, descriptions, and significant quantitative results for the categories found in the drawings. The presence of these categories in the pre/post drawings will be described with illustrative examples.
| Drawing Category Name | Drawing Category Description | Pre/Post Significant Results for Mathematics (n = 72) and Science Drawings (n = 75) |
|---|---|---|
| Increase in Teaching Students as a Component of Learning | Drawing clearly includes a teacher with student(s) | Math: p = .039 Science: p = .004 |
| Decrease in Board/Lecture | Drawing includes a board or teacher at the board | Math: p = .026 Science: p = .009 |
| Increase in Materials for Hands-on Teaching | Drawing contains mathematics manipulative or science materials | Math: p < .001 Science: p = .018 |
| Increase in Students Working Together | Drawing depicts two or more students working together | Math: p = .039 Science: p < .001 |
| Decrease in Uncertainty of Student(s) | Drawing contains question marks, straight face, sad face, text that indicates uncertainty | Math: p < .001 Science: p = .019 |
| Increase in Positive Expression | Drawing contains student(s) with happy face | Math: p = .005 Science: p = .026 |
| Decrease Negative Expression | Drawing contains student(s) with unahppy face | Math: p < .001 Science: p = .008 |
| Increase in Inclusion of Recent Content | Drawing depicts content recently learned in college methods course | Math: p < .001 Science: p = .001 |
Written Descriptions
The pre/post writing data resulted in three significant categories. Analysis of the pre/post mathematics and science written descriptions data resulted in a significant difference, p < .05, in the proportion of three categories pre- and post- methods courses. Table 2 indicates the categories, descriptions, and significant quantitative results for the categories found in the writing. Examples of the writing that show these themes will be provided.
| Written Description Themes | Theme Description | Pre/Post Results for Mathematics (n = 72) and Science Written Descriptions (n = 75) |
|---|---|---|
| Increase in Collaboration | Writing contains examples of working together with other students, discussions, inclusion of hands-on materials, etc. | Mathematics: p = .031 Science: p = .004 |
| Decrease in Negative Emotions | Writing describes negative feelings about learning mathematics or science (e.g., giving up, frustration, irritation, sadness, boredom). | Math: p < .001 Science: p < .001 |
| Increase in Subject-Specific Practices | Writing includes specific pedagogies or practices learned in math/science methods courses (Math: Problem Solving/ Science: 5E) | Math: p = .003 Science: p < .001 |
Increase in Teaching Students as a Component of Learning
PSETs’ drawings of learning mathematics and science showed a significant increase in the presence of a teacher. For example, a pre-drawing could contain a student at a desk with no teacher present and a post-drawing could contain a teacher helping a student at a desk. In math, eight PSETs did not include a teacher before the methods class but included a teacher after the methods class. Figure 2 is an example of a pre-post mathematics drawing. This PSET depicted a student sitting at a desk alone before completing the math methods course and depicted a student at a desk with a teacher after completing the mathematics methods course.

In science, nine drawings that did not contain a teacher in the pre-drawing included a teacher in the post-drawing. Figure 3 is an example of a pre-post science drawing. The PSET included a student alone in the pre-drawing and a group of students with a teacher in the post-drawing.

Decrease in Board/Lecture and Increase in Materials for Hands-on Teaching
The PSETs’ drawings indicated a decrease in lecture-based teaching and an increase in materials for hands-on teaching. In mathematics and science, many PSETs included a board or a teacher at the board in the pre-drawing and, in the post-drawings, included mathematics manipulatives or science materials without a board. In math, 21 PSETs did not include a board after taking the mathematics methods course, and, in science, 22 PSETs did not include a board after taking the science methods course. Figure 4 shows a pre mathematics drawing where the teacher is at the board and students are sitting in rows at desks that are facing the board, a lecture-based teaching setting. Although three PSETs included manipulatives in both their pre and post-drawings, 18 PSETs that did not have manipulatives in their pre-drawing added manipulatives to their post-drawings. The post-drawing shows hands using mathematics manipulatives that include base-ten blocks, counters, fraction circles, and connecting cubes, a reform-based teaching setting.

The PSETs’ science drawings also showed a decrease in lecture and an increase in science materials, similar to the mathematics drawings. Eighteen PSETs included science materials in their pre and post-drawings, but 28 students that did not have science materials in their pre-drawings, added science materials to their post-drawings. Figure 5 shows a PSETs’ pre and post science drawing.

Increase in Students Working Together
We found that the PSETs’ pre-drawings contained individuals, whereas the post-drawings contained groups of people working together. The groups of students collaborating were often depicted as having discussions, indicated with speaking bubbles. In the mathematics drawings, 10 PSETs that did not include students working together in their pre-drawing showed students working together in their post-drawing. Twenty-two PSETs that did not depict students working together in the science pre-drawing drew students working together in the science post-drawing. Figure 6 shows an example of Julia’s pre mathematics and Astrid’s pre science drawing with an individual and Julia’s post mathematics and Astrid’s post science drawing with a group of students.


We also found that PSETs description of their drawings included an increase in collaboration. For example, one PSET, Julia, described her pre-drawing as, “I am sitting in a desk taking notes as the teacher writes important information on the board.” She writes about her post-drawing by saying, “In groups, my classmates and I discuss how we think about mathematics and we use manipulatives to help us figure it out.” Astrid writes, “I picture sitting at a black lab table watching my teacher demonstrate something. In this picture I have to write a lab report and I have no idea what I’m doing” as she describes her pre-drawing. For her post-drawing, she says, “I am working in a group with a lot of hands-on materials. We are writing down our observations about what we notice.”
Decrease in Uncertainty of Students
The mathematics and science pre-drawings depicted students as unsure, and the post-drawings indicated confidence. Uncertainty was shown using a straight or sad face, question marks, or text indicating uncertainty. Confidence was shown with a happy face, exclamation points, or text indicating confidence. This category was seen across the mathematics and science drawings. Although 43 PSETs did not show uncertainty in the pre or post mathematics drawings, 23 PSETs showed uncertainty in their pre-drawings but did not show uncertainty in their post-drawings. In science, 56 PSETs did not depict uncertainty in their pre- or post-drawings, but 15 PSETs showed uncertainty in their pre-drawings, but not in their post-drawings. Figure 7 shows examples from mathematics and science.


Increase in Positive Expression/Decrease in Negative Expression
The drawings showed that there was an increase in positive expressions and a decrease in negative expressions from before the mathematics and science methods classes and after the mathematics and science methods classes. A positive expression is indicated with the presence of a happy face and a negative expression is indicated with the presence of a frown. In both mathematics and science, the number of drawings with a positive expression increased from pre to post and the number of drawings with a negative expression decreased from pre to post. Sixteen PSETs depicted positive expressions in their pre- and post-drawings. However, 27 PSETs that did not show positive expressions in their pre-drawing drew positive expressions in their post-drawing. The science drawings were similar with 34 PSETs showing positive expressions in their pre- and post-drawings, but 21 PSETs that did not have a positive expression in their pre-drawing added a positive expression to their post-drawing. In addition, 70 PSETs’ pre- and post-drawings did not contain a negative expression, but two PSETs that had a negative expression before the mathematics course did not draw a negative expression after the mathematics course. Similarly, in science, 67 PSETs did not have a negative expression in their pre- or post-drawing, but 8 PSETs that had a negative expression before the science course, dropped the negative expression after the science course. Figure 8 shows an increase in a positive expression and a drop in a negative expression in math. The science drawings were very similar.
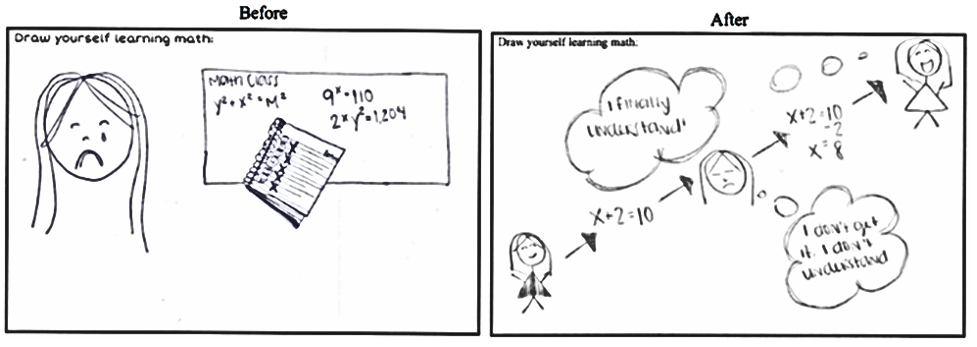
We also found that PSETs’ descriptions of their drawings included a decrease in negative emotions. In math, Kathy described her pre-drawing as, “My drawing is a picture of me, very sad because I made a bad grade on a test. There are also a few complicated problems written on the whiteboard. Let’s say math isn’t my best subject.” However, her post-drawing showed, “As I am introduced to a problem I am frustrated I don’t understand, but that is a part of my process. I finally understand the equation and I am content. The cloud bubbles also represent not just what is written, but my thinking processes to get the new answer” (see Figure 8). Similarly, Tamara, a PSET in science wrote, “I have a bad relationship with science…it was almost as if I didn’t try at it for so long that I gave up.” Her post-drawing shows a definite change in negative emotions, and she described it as, “I still need to work on total content understanding, but I have gotten SO MUCH better with science, both in understanding and my feelings towards it. I feel like I understand major concepts and don’t cry every time I see or hear a science question.”
Increase of Inclusion of Recent Content
The pre-drawings in mathematics most often depicted the content area of algebra because this was the most recent mathematics class that students had taken. Post mathematics drawings contained the content area of numbers and operations because that was the focus of the methods course in which the drawings were collected. Figure 9 shows a pre-drawing that contains algebra and a post-drawing that contains numbers and operations. Twenty-one PSETs in mathematics that showed algebra or calculus in their pre-drawings did not include algebra or calculus from their post-drawings but included the recent content of numbers and operations. Twenty-five PSETs in science that did not have recent content in their pre-drawing added recent course activities to their post-drawing. The pre-drawing in science shows many different content areas including chemistry and biology. The post-drawing shows the most recent content from the methods class (e.g., a recent course activity) (see Figure 10).


Similar to the inclusion of most recent content in PSETs’ drawings, PSETs’ writing showed a significant increase in subject-specific practices. Jamie described her pre math drawing in Figure 9:
One of the many reasons I plan to become an elementary teacher is the lack of complex math classes required. My math background would consist of the typical honors high school courses with some AP calculus involved. If I were to define my feelings towards math, I would say that the effort is there, the lessons are usually retained with work and practice but the interest area is lacking beyond your basic, life-applicable math problem.
When writing about her post mathematics drawing, she remarked, “From this course, I have learned so many new ways to solve problems. Each way provides a different perspective and process to cater to what fits the student best.”
A student in the science methods class, Hilary, commented on her pre-drawing (Figure 10), “I believe science should be hands-on and interactive. This is a picture of myself exploring the world around me.” She remarked about her post science drawing, and said, “This is a picture of me learning science through hands-on activities. The best way to learn science is to ask a question and explore activities to find evidence. Science is [a] way to help us understand the world around us.”
Discussion
Based on the results of this study, PSETs’ experiences in constructivist content-focused methods courses with an internship component seemed to influence PSETs’ perceptions of learning mathematics and science. In particular, PSETs significantly increased their positive emotions and/or decreased their negative emotions related to learning mathematics and science content in their drawings. There was also a decrease in PSETs’ negative emotions in their written explanations. Katz et al. (2010) studied PSETs’ drawings in science after a semester of after-school internship which used constructivist learning tenets in the design. They found an increase in the inclusion of positive expressions and/or a decrease in the inclusion of negative expressions in the PSETs’ drawings (Katz et al., 2010). These findings also align with Akerson’s (2016) results where PSETs’ perceptions towards mathematics shifted from a negative toward a positive experience after completing a field experience where PSETs observed classroom settings where students were learning mathematics in a collaborative setting and engaged in discussion with each other. These findings have important implications for how enthusiastic PSETs feel about teaching these content areas, given that researchers have found links between PSETs’ attitudes towards their content, their approaches to teaching the subject (Wilson & Kittleson, 2012; Hsu et al., 2017), and in the case of science, even how often they are willing to teach it (Cavallo et al., 2002).
Additionally, we saw significant increases about content-related understanding. Content understanding is an important component in the development of a constructivist teaching identity, as this strategy of attending to student ideas requires higher-level knowledge of the teacher (Windschitl, 1999). In PSETs’ drawings, from pre- to post- they increased the inclusion of recent content from the model constructivist activities used in class as well as decreased the uncertainty expressed about their content understanding. In their written explanations, PSETs showed an increase in discussion of subject-specific practices.
We agree with Langer-Osuna & Esmonde (2017) that as PSETs reflected and made sense of their experiences of learning mathematics and science through drawing and written descriptions, they told stories about their mathematical and scientific selves. Similar to Battey and Franke’s (2008) findings that shifts existed in teacher identities based on stories before and after participating in professional development, we found that PSETs showed evidence of shifting identities based on drawings completed before and after engaging in methods courses.
Implications for Teaching
The results of this study provide implications for mathematics and science teacher educators, especially those that teach methods courses to PSETs. Providing model experiences related to reform-based teaching is what pre-service teachers expect (Timoštšuk & Ugaste, 2010) and may be an important element in shifting their emotional responses to content-area teaching. After experiencing model constructivist mathematics or science teaching, PSETs increased their inclusion of elements associated with constructivist learning environments (materials for hands-on teaching and students working together) and decreased their inclusion of passive elements of learning (board/lecture) in their drawings as well as included an increase in written expressions of collaboration with peers as a component of learning.
While we saw significant increases in PSETs’ inclusion of aspects of reform-based teaching practices in their post-drawings and explanations, we are only cautiously optimistic that this will result in the consistent use of these practices in their classroom teaching. Research has found that new science teachers will often espouse the use of reform-based practices in their classrooms, but not implement these (Davis et al., 2006). Despite being exposed to constructivist ideas in university classes, teachers tend to use strategies based on their personal learning histories (Eick & Reed, 2002). In addition, if PSETs have had negative emotions about their learning of the subject, they may choose to plan more passive learning for their students to prevent them from struggling (Wilson & Kittleson, 2012). Finally, even science teacher enthusiasts, who have expressed positive experiences about learning and teaching science, struggle to consistently teach science because of constraints related to time, resource availability, and testing for other subjects (Bradbury & Wilson, 2020). Therefore, even though we see potential in using both modeling of reform-based teaching strategies and reflection on their perspectives of content-area learning throughout the semester, their experiences in the methods courses are only one small set of their learning experiences.
Limitations and Suggestions for Future Research
This study gave us a glimpse into how PSETs’ identities related to learning mathematics and science develop in a social context like a classroom. Limitations exist connected to PSETs’ abilities and willingness to draw themselves. Thus, the method of using drawings as evidence of learning could be paired with using narrative identities where PSETs reflect and make sense of their experiences of learning mathematics and science through telling stories (Langer-Osuna & Esmonde, 2017; Battey & Franke, 2008). In future studies, it would be beneficial to explore how PSETs’ identities develop in other instructional settings, such as field experiences and online, asynchronous, and blended mathematics methods courses. Research should also be done to examine drawings before and after methods courses, as well as after student teaching, to locate possible shifts in instructional practice and for teacher educators to improve their courses. In addition, future studies should also address how PSETs’ perceptions of themselves as learners of mathematics and science impact how they design and teach lessons to students. In future research, mathematics and science teacher educators could use pre- and post-course drawings of students learning along with drawings of students teaching to try to analyze connections between PSETs’ ideas about learning and teaching elementary mathematics and science.
References
Adams, G. (2013). Women teachers’ experiences of learning mathematics. Research in Mathematics Education, 15(1), 87–88. https://doi.org/10.1080/14794802.2013.763607
Akerson, A. (2016). Preservice Teachers’ Perceptions of Mathematics through Drawings–RESEARCH. Kentucky Journal of Excellence in College Teaching and Learning, 14, 3. https://encompass.eku.edu/kjectl/vol14/iss/3/
Andrew, P. B. (2004). Decreasing math anxiety in college students. College Student Journal, 38(2), 321–323. https://eric.ed.gov/?id=EJ704967
Avraamidou, L. (2014a). Tracing a beginning elementary teacher’s development of identity for science teaching. Journal of Teacher Education, 65(3), 223-240. https://doi.org/10.1177/0022487113519476
Avraamidou, L. (2014b). Studying science teacher identity: Current insights and future research directions. Studies in Science Education, 50(2), 145-179. https://doi.org/10.1080/03057267.2014.937171
Bartholomew, H., Darragh, L., Ell, F., & Saunders, J. (2011). ‘I’m a natural and I do it for love!’: Exploring students’ accounts of studying mathematics. International Journal of Mathematical Education in Science and Technology, 42(7), 915-924. https://doi.org/10.1080/0020739X.2011.608863
Battey, D., & Franke, M. (2008). Transforming identities: Understanding teachers across professional development and classroom practice. Teacher Education Quarterly, 35(3), 127-149. https://eric.ed.gov/?id=EJ831720
Bekdemir, M. (2010). The pre-service teachers’ mathematics anxiety related to depth of negative experiences in mathematics classroom while they were students. Educational Studies in Mathematics, 75(3), 311-328. https://www.jstor.org/stable/40928564
Beltman, S., Glass, C., Dinham, J., Chalk, B., & Nguyen, B. (2015). Drawing identity: Beginning pre-service teachers’ professional identities. Issues in Educational Research, 25(3), 225. https://www.jstor.org/stable/40928564
Bradbury, L.U., & Wilson, R.E. (2020). Questioning the prevailing narrative about elementary science teachers: An analysis of the experiences of science teacher enthusiasts. Science Education, 104(3), 421-445. https://doi.org/10.1002/sce.21574
Brooks, M. (2009). What Vygotsky can teach us about young children drawing. International Art in Early Childhood Research Journal, 1(1), 1-13. https://rune.une.edu.au/web/handle/1959.11/5428
Burton, M. (2012). What is math? Exploring the perception of elementary pre-service teachers. Issues in the undergraduate mathematics preparation of school teachers, 5, 1-17. https://eric.ed.gov/?id=EJ970350
Common Core State Standards Initiative. (2010). Common Core State Standards for Mathematics (CCSSM). Washington, DC: National Governors Association Center for Best Practices and the Council of Chief State School Officers.
Caldwell, H., & Moore, B. H. (1991). The art of writing: Drawing as preparation for narrative writing in the primary grades. Studies in Art Education, 32(4), 207-219. https://doi.org/10.2307/1320873
Carlile, O., & Jordan, A. (2005). It works in practice but will it work in theory? The theoretical underpinnings of pedagogy. In O’Neill, G., Moore, S., & McMullin, B. (Eds.), Emerging Issues in the Practice of University Learning and Teaching (pp. 11-26). Dublin Institute of Technology.
Carrier, S. J., Whitehead, A. N., Walkowiak, T. A., Luginbuhl, S. C., & Thomson, M. M. (2017). The development of elementary teacher identities as teachers of science. International Journal of Science Education, 39(13), 1733-1754. https://doi.org/10.1080/09500693.2017.1351648
Cavallo, A. M. L., Miller, R. B., & Saunders, G. (2002). Motivation and affect toward learning science among preservice elementary teachers: Implications for classroom teaching. Journal of Elementary Science Education, 14(2), 25-38. https://doi.org/10.1007/BF03173846
Charmaz, K. (2010). Grounded theory as an emergent method. In Hesse-Biber, S. N., & Leavy, P. (Eds.). Handbook of emergent methods (pp. 155-172). Guilford Press.
Clift, R. T., & Brady, P. (2005). Research on methods courses and field experiences. In M. Cochran-Smith & M. Kenneth (Eds.), Studying teacher education: The report of the AERA panel on research and teacher education (pp. 309-424). Lawrence Erlbaum.
Cobb, P. (1988). The tension between theories of learning and instruction in mathematics education. Educational Psychologist, 23(2), 87-103. https://doi.org/10.1207/s15326985ep2302_2
Cohen, D. K., & Ball, D. L. (1999). Instruction, capacity, and improvement. (CPRE Research Report No. RR-043). Retrieved from Study of Instructional Improvement website: http://www.sii.soe.umich.edu/about/pubs.html
Davis, E. A., Petish, D., & Smithey, J. (2006). Challenges new science teachers face. Review of Educational Research, 76(4), 607-651. https://doi.org/10.3102/00346543076004607
Drake, J. E., & Winner, E. (2013). How children use drawing to regulate their emotions. Cognition & Emotion, 27(3), 512-520. https://doi.org/10.1080/02699931.2012.720567
Eick, C. J., & Reed, C. J. (2002). What makes an inquiry‐oriented science teacher? The influence of learning histories on student teacher role identity and practice. Science Education, 86(3), 401-416. https://doi.org/10.1002/sce.10020
Fosnot, C. T. (1996). Constructivism: A psychological theory of learning. In C. T. Fosnot (Ed.), Constructivism: Theory, perspectives, and practice (pp. 8-33). Teachers College Press.
Frank, M. L. (1990). What myths about mathematics are held and conveyed by teachers? Arithmetic Teacher, 37(5), 10–12. https://eric.ed.gov/?id=EJ407573
Gresham, G. (2007). A study of mathematics anxiety in pre-service teachers. Early Childhood Education Journal, 35(2), 181–188. https://doi.org/10.1007/s10643-007-0174-7
Hadfield, O. D., & McNeil, K. (1994). The relationship between Myers-Briggs personality type and mathematics anxiety among pre-service elementary teachers. Journal of Instructional Psychology, 21(4), 375–384.
Harper, N. W., & Daane, C. J. (1998). Causes and reduction of math anxiety in preservice elementary teachers. Action in Teacher Education, 19(4), 29-38. https://doi.org/10.1080/01626620.1998.10462889
Hembree, R. (1990). The nature, effects, and relief of mathematics anxiety. Journal for Research in Mathematics Education, 33-46. https://doi.org/10.2307/749455
Hsu, P-L., Reis, G., & Monarrez, A. (2017). Identity discourse in preservice teachers’ science learning autobiographies and science teaching philosophies. Canadian Journal of Science, Mathematics, and Technology Education, 17(3), 179-198. https://doi.org/10.1080/14926156.2017.1343517
Huang, J., Wang, Y., & Teng, F. (2021). Understanding changes in teacher beliefs and identity formation: A case study of three novice teachers in Hong Kong. Teaching Education, 32(2), 193–207. https://doi.org/10.1080/10476210.2019.1693535
Jackson, C. D., & Leffingwell, R. J. (1999). The role of instructors in creating math anxiety in students from kindergarten through college. The Mathematics Teacher, 92(7), 583-586. https://www.jstor.org/stable/27971118
Katz, P., McGinnis, J.R., Hestness, E., Riedinger, K., Marbach-Ad, G., Dai, A., & Pease, R. (2010). Professional identity development of teacher candidates participating in an informal science education internship: A focus on drawings as evidence. International Journal of Science Education, 33(9), 1169-1197. https://doi.org/10.1080/09500693.2010.489928
Kazempour, M. (2008). Exploring attitudes, beliefs, and self efficacy of pre-service elementary teachers enrolled in a science methods course and factors responsible for possible changes (Doctoral dissertation). Retrieved from ProQuest, LLC. (3324538).
Kazempour, M. (2013). The interrelationship of science experiences, beliefs, attitudes, and self-efficacy: A case study of a pre-service teacher with positive science attitude and high science teaching self-efficacy. European Journal of Science and Mathematics Education, 1(3), 106-124. https://eric.ed.gov/?id=EJ1108231
Langer-Osuna, J. M., & Esmonde, I. (2017). Identity in research on mathematics education. In Cai, J. (Ed.), Compendium for research in mathematics education (pp. 637-648). National Council of Teachers of Mathematics.
Lave, J., & Wenger, E. (1991). Situated learning: Legitimate peripheral participation. Cambridge University Press.
Lee, J. E., & Zeppelin, M. (2017). Using drawings to bridge the transition from student to future teacher of mathematics. International Electronic Journal of Elementary Education, 6(2), 333-346. Retrieved from https://www.iejee.com/index.php/IEJEE/article/view/48
Luehmann, A. L. (2007). Identity development as a lens to science teacher preparation. Science Education, 91(5), 822-839. https://doi.org/10.1002/sce.20209
Lortie, D. (1975). Schoolteacher: A sociological study. Chicago University Press. Mensah, F. M. (2011). The DESTIN: Preservice teachers’ drawings of the ideal elementary science teacher. School Science and Mathematics, 111(8), 379-388. https://doi.org/10.1111/j.1949-8594.2011.00103.x
Mensah, F. M. & Fleshman, R. (2017). Drawings as identity data in elementary science teacher education. In Katz, P. (Ed.), Drawing for Science Education: An International Perspective (pp. 219-225). Sense Publishers. DOI:10.1007/978-94-6300-875-4
Mihalko, J. C. (1978). The answers to the prophets of doom: Mathematics teacher education. In D.B. Aichele (Ed.), Mathematics Teacher Education: Critical Issues and Trends (pp. 36-41).
National Education Association. National Council of Teachers of Mathematics (NCTM). (2014). Principles to actions: Ensuring mathematical success for all. Author.
National Research Council. (2001). Adding it up: Helping children learn mathematics. J. Kilpatrick, J. Swafford, & B. Findell (Eds.). Mathematics Learning Study Committee, Center for Education, Division of Behavioral and Social Sciences and Education. National Academy Press.
National Research Council. (2007). Knowing what students know: The science and design of educational assessment. J. Pelligrino, N. Chudowsky, & R. Glaser (Eds.). Committee on the Foundations of Assessment, Board on Testing and Assessment, Center for Education, Division of Behavioral and Social Sciences and Education. National Academy Press.
National Research Council. (2012). A framework for K-12 science education: Practices, crosscutting concepts, and core ideas. National Academies Press.
Perry, A. B. (2004). Decreasing mathematics anxiety in college students. College Student Journal, 38(2), 321–324. https://eric.ed.gov/?id=EJ704967
Picone-Zocchia, J., & Martin-Kniep, G. O. (2008). Supporting mathematical learning: Effective instruction, assessment, and student Activities, grades K-5. Jossey-Bass.
Rivera Maulucci, M. S. (2013). Emotions and positional identity in becoming a social justice science teacher: Nicole’s story. Journal of Research in Science Teaching, 50(4), 453-478. https://doi.org/10.1002/tea.21081
Rodd, M., & Bartholomew, H. (2006). Invisible and special: Young women’s experiences as undergraduate mathematics students. Gender and Education, 18(1), 35-50. https://doi.org/10.1080/09540250500195093
Rule, A. C., & Harrell, M. H. (2006). Symbolic drawings reveal changes in preservice teacher mathematics attitudes after a mathematics methods course. School Science and Mathematics, 106(6), 241-258. https://doi.org/10.1111/j.1949-8594.2006.tb17913.x
Sfard, A., & Prusak, A. (2005). Telling identities: In search of an analytic tool for investigating learning as a culturally shaped activity. Educational Researcher, 34(4), 14-22. https://doi.org/10.3102/0013189X034004014
Siegal, S., & Castellan Jr, N. J. (1988). Nonparametric statistics for the Behavioral Sciences. McGraw-Hill.
Solomon, Y. (2007). Not belonging? What makes a functional learner identity in undergraduate mathematics? Studies in Higher Education, 32(1), 79–96. https://doi.org/10.1080/03075070601099473
Stipek, D. J., Givvin, K. B., Salmon, J. M., & MacGyvers, V. L. (2001). Teachers’ beliefs and practices related to mathematics instruction. Teaching and teacher education, 17(2), 213-226. https://doi.org/10.1016/S0742-051X(00)00052-4
Timoštšuk, I., & Ugaste, A. (2010). Student teachers’ professional identity. Teaching and Teacher Education, 26(8), 1563-1570. https://doi.org/10.1016/j.tate.2010.06.008
Vinson, B. (2001). A comparison of preservice teachers’ mathematics anxiety before and after a methods class emphasizing manipulatives. Early Childhood Education Journal, 29(2), 89-94. https://doi.org/10.1023/A:1012568711257
Vygotsky, L. (1978). Mind in society: The development of higher psychological processes. Harvard University Press.
Wenger, E. (1999). Communities of practice: Learning, meaning, and identity. Cambridge University Press.
Williams, J. (2011). Teachers telling tales: The narrative mediation of professional identity. Research in Mathematics Education, 13(2), 131–142. https://doi.org/10.1080/14794802.2011.585825
Wilson, R.E. & Kittleson, J. (2012). The role of struggle in pre-service elementary teachers’ experiences as students and approaches to facilitating science learning. Research in Science Education, 42(4), 709-728. DOI 10.1007/s11165-011-9221-x
Windschitl, M. (1999). The challenges of sustaining a constructivist classroom culture. Phi Delta Kappan, 80(10), 751. https://eric.ed.gov/?id=EJ587664
Zeichner, K. M., & Tabachnick, B. R. (1981). Are the effects of university teacher education ‘washed out’ by school experience? Journal of Teacher Education, 32(3), 7-11. https://doi.org/10.1177/002248718103200302
Appendix A
| Drawing Category Name for Mathematics and Science | Pre/Post Results for Mathematics (n = 72) and Science Drawings (n = 75) | |
|---|---|---|
| Mathematics p = | Science p = | |
| Books/papers | .359 | .441 |
| Computer/internet | 1.000 | .289 |
| Drawing on paper/board | .375 | 1.000 |
| Writing on paper/board | .690 | .332 |
| Symbols on paper/board | .250 | 1.000 |
| Teaching students | .039 | .004 |
| Desk/table | 1.000 | .164 |
| Board | .026 | .009 |
| Windows | 1.000 | .219 |
| Mathematics Manipulatives/Science Materials | <.001 | .018 |
| Pencil | .481 | .754 |
| Ruler | 1.000 | .625 |
| Calculator | .031 | 1.000 |
| No person | 1.000 | 1.000 |
| Student alone | .700 | .429 |
| Teacher alone | 1.000 | 1.000 |
| With other students working separately | .289 | .180 |
| With other students working together | .039 | <.001 |
| With a teacher (unknown gender) | 1.000 | .064 |
| With a teacher (known male) | 1.000 | 1.000 |
| With a teacher (known female) | .388 | 1.000 |
| Parent/expert | .500 | 1.000 |
| Teacher in front of class | .383 | .064 |
| Teacher off to the side | 1.000 | 1.000 |
| Teacher with a student | 1.000 | 1.000 |
| Student at the board | .238 | 1.000 |
| Student at desk/table | .845 | .441 |
| Centers | 1.000 | .250 |
| Indoors | 1.000 | 1.000 |
| Student thinking cloud: connections to content | <.001 | .289 |
| Student thinking cloud:? or uncertainty | <.001 | .019 |
| Student speaking bubble: ? or uncertainty | .375 | .453 |
| Student positive expression | .005 | .026 |
| Student negative expression | <.001 | .008 |
| Student neutral or no expression | 1.000 | .201 |
| Teacher positive expression | .629 | .454 |
| Teacher negative expression | .500 | 1.000 |
| Teacher neutral or no expression | 1.000 | .289 |
| Drawing Category Name for Math | p = |
|---|---|
| Basic operations present | 1.000 |
| Algebra present | <.001 |
| Geometry present | .625 |
| Contrast between arithmetic and “other” mathematics content | .063 |
| Drawing Category Name for Science | p = |
|---|---|
| Earth science | .001 |
| Biology | .009 |
| Physical science | .405 |
| 5E | .063 |
Appendix B
| Drawing Category Name for Mathematics and Science | Pre/Post Results for Mathematics (n = 72) and Science Drawings (n = 75) | |
|---|---|---|
| Mathematics p = | Science p = | |
| Hands-on | .002 | .188 |
| Text | 1.000 | .049 |
| Media | 1.000 | .021 |
| Writing | .092 | .092 |
| Collaboration | .031 | .004 |
| Lecture | .008 | .070 |
| Activity from class | 1.000 | .832 |
| Positive | .230 | .596 |
| Negative | < .001 | < .001 |
| World outside | 1.000 | |
| Writing Category Name for Math | p = |
|---|---|
| Problem solving | .003 |
| Reasoning and proof | .039 |
| Communication | .500 |
| Connections | .063 |
| Representations | .688 |
| Numbers and operations | .549 |
| Geometry | .500 |
| Fractions | .250 |
| Writing Category Name for Math | p = |
|---|---|
| Problem solving | .003 |
| Reasoning and proof | .039 |
| Communication | .500 |
| Connections | .063 |
| Representations | .688 |
| Numbers and operations | .549 |
| Geometry | .500 |
| Fractions | .250 |
| Writing Category Name for Science | p = |
|---|---|
| 5E | < .001 |
| Experimenting | .571 |
| Recording | .219 |
| Observing | .804 |
| Data collection | .375 |
| Engaging in argument from evidence | .500 |
| Asking questions | .031 |
| Mathematical thinking | 1.000 |
| Inferring | .500 |
| Measuring | 1.000 |
| Modeling | .125 |
| Earth science | 1.000 |
| Life science | <.001 |
| Physical science | .041 |
