8 The Simplex Method Using Pivot Tables

Robert Vanderbei, Operations Research and Financial Engineering Professor at Princeton has created an online solver for the simplex method.  To see how this problem would be solved using this, or a similar software solver, let’s walk through the steps here.

The constraints previously were converted to the following objective function and equalities.

[latex]f(x_a,x_b)=10x_a+12x_b[/latex]

[latex]4x_a+4x_b+u=600[/latex]

[latex]3x_a+2x_b+v=500[/latex]

[latex]2x_a+4x_b+w=500[/latex]

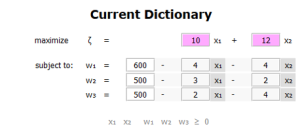These are entered as the dictionary shown to the right.  A dictionary is much like a tableau and is pivoted repeatedly until the solution can be read from the dictionary.  In the dictionary, [latex]x_1[/latex] and [latex]x_2[/latex] correspond to [latex]x_a[/latex] and [latex]x_b[/latex] in the previous tableaux and [latex]w_1[/latex], [latex]w_2[/latex], and [latex]w_3[/latex] correspond to [latex]u[/latex], [latex]v[/latex], and [latex]w[/latex] respectively.

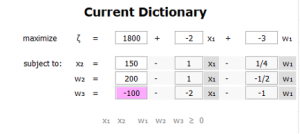Continuing through the example, we will choose to pivot on the variable [latex]x_2[/latex] and will pivot it with [latex]w_1[/latex].  The pink highlights on both [latex]x_1[/latex] and [latex]x_2[/latex] suggest that either will suffice for a pivot.  We chose [latex]x_2[/latex] because it has the greater of the two coefficients and changes to it will cause a greater increase than changes to [latex]x_1[/latex]. To accomplish the pivot, click on the box labelled [latex]x_2[/latex] in the line starting with [latex]w_1=[/latex].  After pivoting [latex]x_2[/latex] with [latex]w_1[/latex], we get the second dictionary to the right.  We still need to pivot [latex]x_1[/latex], and the tool recommends pivoting with [latex]w_3[/latex] by showing the pink highlight.  Clicking on the [latex]x_1[/latex] box in the line starting with [latex]w_3=[/latex] gives us the final dictionary.

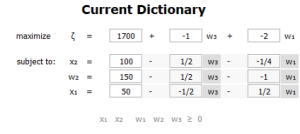From this dictionary, remembering that the slack variables are equal to zero, we can read off the solution [latex]x_2 = 100[/latex] and [latex]x_1 = 50[/latex]. This agrees with the solution we attained using the tableau method above.