3 The Feasible Region
James Kupetz; Earl Lee; Karl Levy; and Daphne Skipper
A solution to a linear program is an assignment of a number to each of the decision variables. For example, [latex](T,C)=(6,0)[/latex] is a solution to the Legos problem that represents making six tables and no chairs.
A feasible solution to a linear program is a solution that satisfies all of the constraints. The solution [latex](T,C)=(6,0)[/latex] to the Legos problem is a feasible solution because it satisfies all four constraints: it does not overuse large or small blocks (constraints 1 and 2), and it does not require making a negative number of tables or chairs (constraints 3 and 4).
An infeasible solution is a solution that is not feasible; that is, a solution is infeasible if it violates at least one constraint.
The value of a solution is the value of the objective function at that solution.
A constraint is active at a particular solution if the constraint is satisfied with equality. Constraints 1 and 4 are active for solution [latex](6,0)[/latex].
Problem 4:
Problem 4. For each of the solutions, [latex](T,C)[/latex], to the Legos problem below: (i) Determine whether the solution is feasible or infeasible. (ii) If the solution is feasible, determine which constraints in the Lego LP are active. If the solution infeasible, determine which constraints are violated. (iii) Find the value of the solution.
- [latex](4,4)[/latex]
- [latex](2,8)[/latex]
- [latex](-1,10)[/latex]
- [latex](0,9)[/latex]
Solution
- (i) Feasible, (ii) [latex]2T+C\le12[/latex] is active, (iii) 104
- (i) Infeasible, (ii) [latex]2T+2C\le18[/latex] has been violated, (iii) 112
- (i) Infeasible, (ii) [latex]T\ge0[/latex] has been violated, (iii) 84
- (i) Feasible, (ii) [latex]2T+2C\le18[/latex] and [latex]T\ge0[/latex] are active, (iii) 90
For two-dimensional linear programs (those with two variables), we can visualize the set of points that satisfy each constraint in the Cartesian plane. A 2-dimensional linear inequality, such as [latex]2T+C\le12[/latex], describes a half-plane: all the points on the line [latex]2T+C=12[/latex], along with the points to the left of (or below) this line.
Figure 1 illustrates the half-planes described by the four constraints of the Legos LP. For example, the shaded region in Figure 1a consists of all of the solutions to the Legos LP that satisfy constraint 1, or that do not require more than 12 large blocks.
Figure 1: Half-planes described by the constraints of the Legos LP
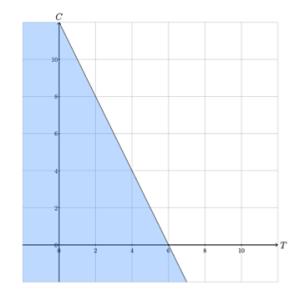
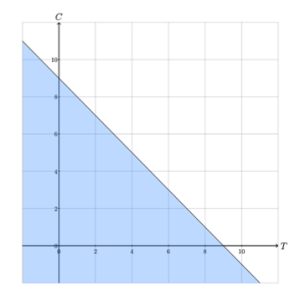
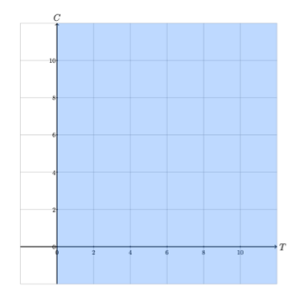
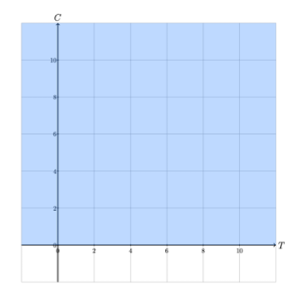
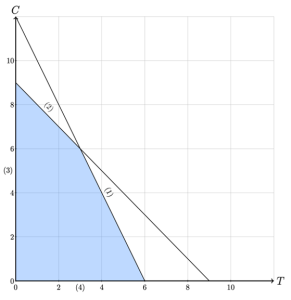
The feasible region of a linear program is the set of solutions that satisfy all constraints. The feasible region of the Legos LP consists of the points in the intersection of all four half-planes described by its constraints, as illustrated in Figure 1. The feasible region of the Legos LP is illustrated in Figure 2. Thus, every point in the shaded region in Figure 2 represents a valid solution to the Legos problem.
Figure 2: Feasible Region of the Legos LP
A linear program is infeasible if its feasible region is empty (in other words, the linear program has no feasible solutions).
A feasible region is unbounded if one or more decision variables can increase (or decrease) indefinitely inside of the feasible region. In this case, the linear program may be unbounded, meaning that there is no optimal solution because the values of .
Problem 5
Suppose the inequalities are the constraints of a linear program. Graph the feasible region of each linear program. Is the associated linear program infeasible?
-
[latex]2x+y\le4[/latex]
[latex]x+2y\le6[/latex]
[latex]y\ge0[/latex]
[latex]y\ge0[/latex] -
[latex]-2x+y\le-4[/latex]
[latex]x+2y\le1[/latex]
[latex]y\ge0[/latex]
[latex]y\ge0[/latex] -
[latex]2x-y\le-3[/latex]
[latex]x-2y\le6[/latex]
[latex]y\ge0[/latex]
[latex]y\ge0[/latex]
Solutions
- A graph of these constraints looks like the figure below. The feasible region is the polygon with vertices [latex](0,0)[/latex],[latex](0,3)[/latex],[latex]\left(\frac{2}{3},\frac{8}{3}\right)[/latex], and [latex](2,0)[/latex]. Any of the points in the region or on its boundary satisfy all four constraints.
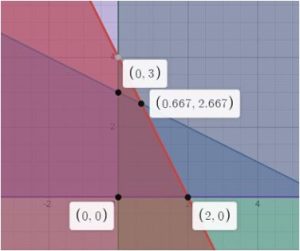 Problem 5b, Feasible Region
Problem 5b, Feasible Region - This is an example of a system that is infeasible. The constraints do not create a region where all four solutions overlap. The system is illustrated in the figure below.
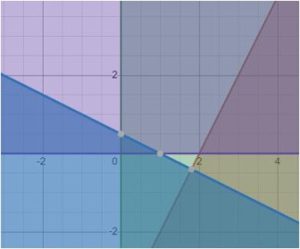 Problem 5b, No Feasible Solutions
Problem 5b, No Feasible Solutions - This is an example of an unbounded feasible region. The feasible region has corners at [latex](0,0)[/latex],[latex](0,3)[/latex], and [latex](6,0)[/latex], but extends without bound between the lines [latex]2x-y=-3[/latex] and [latex]x-2y=y[/latex] as [latex]x[/latex] and [latex]y[/latex] increase to infinity.
