4 Solving the Legos LP
James Kupetz; Earl Lee; Karl Levy; and Daphne Skipper
Let's consider the Legos LP again:
[latex]2T+2C\le18[/latex]
[latex]T\ge0[/latex]
[latex]C\ge0[/latex]
(2)
(3)
(4)
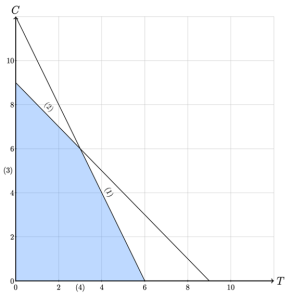
The feasible region of the Legos LP is made up of the polygon with corners [latex](0,0)[/latex], [latex](6,0)[/latex], [latex](0,9)[/latex], and [latex](3,6)[/latex], as illustrated in Figure 4-1. These corner points are called basic feasible solutions, of the LP. These points are important in solving a linear program because at least one of these points must be an optimal solution!
Figure 4-1: Feasible Region of the Legos LP
Theorem 1
If P is a linear program with a bounded, nonempty, feasible region, then an optimal solution to P occurs at a basic feasible solution.
Note the requirement in Theorem 1 that the feasible region of P is bounded and nonempty. Without these requirements, there are three possible cases given a linear program P:
(1) P has an optimal solution, (2) P is unbounded (i.e., the objective function can grow without bound within the feasible region), or (3) P is infeasible. The requirement that the feasible region of P is bounded and nonempty keeps us in case (1), our case of interest.
Thus, we can solve the Legos problem by evaluating the objective function at each of the corner points of the feasible region to see which results in the maximum revenue:
[latex]R(0,0)=0[/latex]
[latex]R(0,9)=90[/latex]
[latex]R(3,6)=108[/latex]
[latex]R(6,0)=96[/latex]
Of the four corner points, [latex](3,6)[/latex] results in the maximum revenue. Thus, by Theorem 1, the optimal solution to the Legos problem is to make 3 tables and 6 chairs for a revenue of $108.
Problem 6:
Use Theorem 1 to solve the LP below.
[latex]2x+2y\le11[/latex]
[latex]x\ge0[/latex]
[latex]y\ge0[/latex]
Solution
By graphing the feasible region of the LP, we see that the corner points are [latex](0,0)[/latex], [latex](0,3)[/latex], [latex]\left(\frac{2}{3},\frac{8}{3}\right)[/latex], and [latex](2,0)[/latex]. Evaluating the objective at each of these points, we see that [latex](2,0)[/latex] results in the maximum objective value of 12. Thus, by Theorem 1, the optimal solution is [latex](2,0)[/latex].
Problem 7:
Consider the following linear program:
[latex]2x+y\le4[/latex]
[latex]x+2y\le6[/latex]
[latex]x\ge0[/latex]
[latex]y\ge0[/latex]
- Graph the feasible region and find the corner points.
- Solve the LP. What do you notice?
Solution
By graphing the feasible region of the LP, we see that the corner points are [latex](0,0)[/latex], [latex](0,5)[/latex], [latex](1.5,4)[/latex], [latex](3.4,2.1)[/latex], and [latex](4,0)[/latex]. The two corner points [latex](1.5,4)[/latex] and [latex](3.4,2.1)[/latex] both result in the same maximum objective value of 5.5. In fact, all of the point on the line segment connecting [latex](1.5,4)[/latex] and [latex](3.4,2.1)[/latex] are optimal solutions to the LP.
