9 Section I: Mary Boole, String Art, and Modular Arithmetic

About Mary Everest Boole

String art, also known as curve stitching, was invented by mathematician Mary Everest Boole in the 19th century as a way to help students better understand various mathematical patterns. Before we learn a bit more about string art, let’s learn more about Mary Everest Boole.

Mary Everest Boole was born in 1832 in the village of Wickwar, Gloucestershire, England. She spent time in rural France as a child and returned to England in 1843. She met George Boole (a mathematician known for the creation of Boolean logic) at the age of 18 and they were married five years later. Together they had five daughters including mathematician Alice Boole Stott. Mary had many occupations during her lifetime including librarian, teacher, secretary, and published author. She died in 1916 at the age of 84.

Using the references listed at the end of Part I (or those of your choosing), answer the following questions about Mary Everest Boole:

Question 1. 

Question 2. 

Question 3.

About String Art

Now that we know a bit more about Mary Everest Boole, let’s explore string art. Our first example will involve working with modular arithmetic and polygons. Most of the arithmetic you have done to this point in your life has likely been based on the real number line.

When you add you move forward. When you subtract you move backwards. And you can keep adding and subtracting in both directions for as long as you like and you’ll never run out of numbers!

But, what happens if we were to limit the numbers we had available to us and turn that number line into a circle! Let’s say we only have the numbers from 1 to 12. We form a circle with these numbers and do arithmetic.

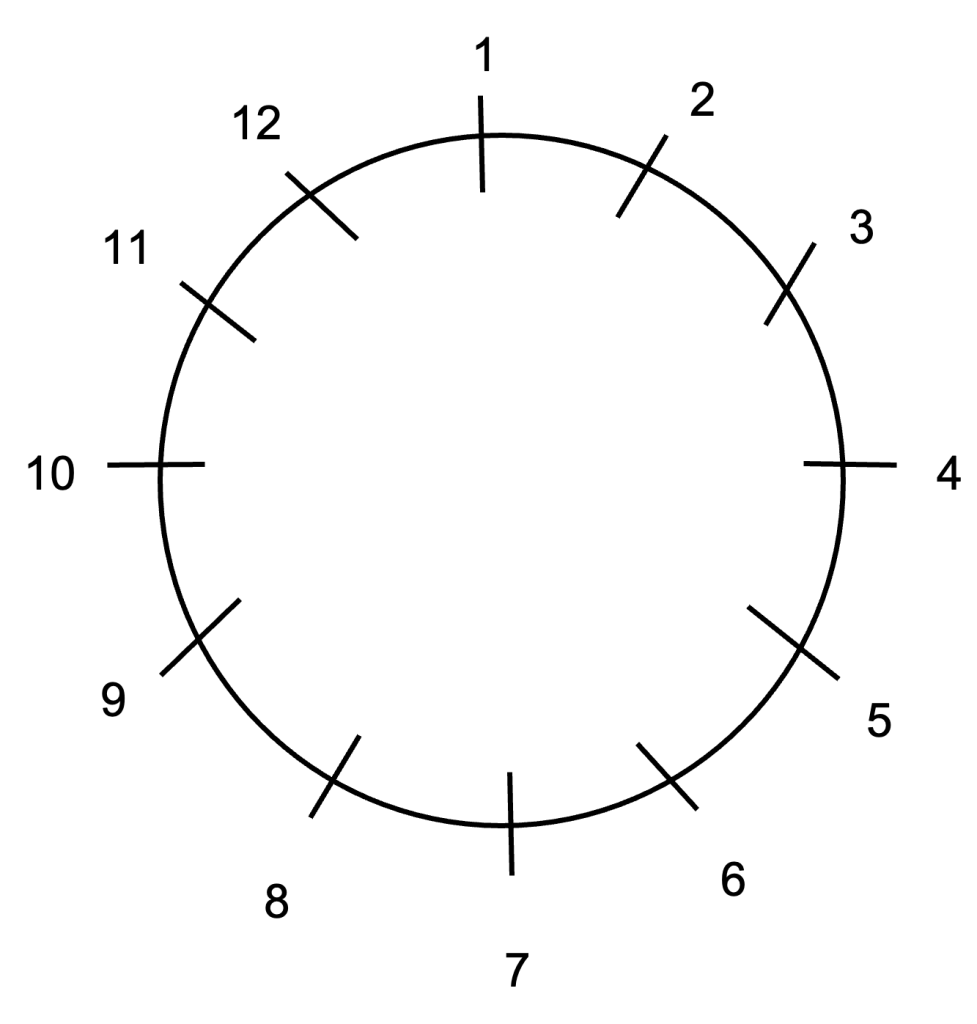
Let’s try some arithmetic.

Question 4.

Question 5.

Question 6.

Question 7.

Question 8.

This might even be familiar to you! This is how we do clock arithmetic! This number system is called the integers modulo 12 and is denoted by Z₁₂. The only subtle change we will make is we’ll turn 12 into 0 and use the numbers 0 up to 11 instead of 1 to 12. The clock arithmetic you were just doing is known as modular arithmetic and can be done with any modulus n where n is any positive integer.

We want to explore some of the really interesting patterns that exist in modular arithmetic and we are going to do that using string art.

Materials needed:

• Printed dot templates given in the Appendix (best if printed on cardstock)
• Large sewing needles
• Colorful yarn or string (the first example requires about 9 ft of string)

Continuing our work in Z₁₂, the Appendix has one template you can use to explore the features of Z₁₂.

First, we are going to connect every fourth dot. The amount we are adding modulo n to get to the next dot will be called the connection number.  In this case the connection number is four. So, in other words, we will have a string from 0 to 4, 1 to 5, 2 to 6, and so on.  In the set of steps below, the front side of your paper is the side with the printed dots, and the back side of your paper is blank.

1. Start by putting your needle through the 0 dot from the back side of the paper so that the needle (and almost all of the string) are now on the front side of your paper (the side with the dots). See picture (a). Tie a knot near the end of the string that is on the back side of the paper.
2. Put your needle down into the paper at the 4 dot. On the back side, send your needle through 1 and then you will be back on the front and you can do 1 to 5. See picture (b).
3. Once your needle is on the back side again send it over to 2.
4. Continue this until every dot has been used twice (and before you start to repeat lines). Pictures (c) and (d) show the front and back (respectively) after three connections.
   1. 
   2. 
   3. 
   4. 

Consider the following:

Question 9:

Now do this same process using the same dot pattern, but this time use a connection number of five.

Question 10:

Question 11:

A Guided Exploration

Now it is your turn to create string art. Note: there is one other template in the appendix that could be used for inspiration or a starting point. Some options for exploration:

• Change the modulus (the total number of dots)-consider primes versus composites.
• Change the starting shape (circle, square, polygon, etc.).
• Change the connection number. You can even use different connection numbers on the same dot pattern (maybe use different string colors).

Some questions to consider once you create new string art:

1. Which string art creations are most interesting and why are they so interesting?
2. What mathematical properties of the numbers/shapes you choose make these so interesting?

Glossary

Connection number

In a given Z_n, an integer value k between 1 and n-1 that tells us that every kth dot will be connected in our string art diagram

Modular arithmetic

Arithmetic that uses whole numbers where these numbers are replaced by their remainders after division by a fixed number known as the modulus

Modulus

The positive whole number used as the fixed divisor in modular arithmetic

Z_n

The set of integers modulo n, i.e. the set {0,1,2,…,n-1} where addition is performed using modular arithmetic.

References

Chas, M. The Extraordinary Case of the Boole Family. Notices of the American Mathematical Society 2019, 66 (11), 1853–1866 DOI: 10.1090/noti1996.

Michalowicz, K. D. Mary Everest Boole (1832-1916): An Erstwhile Pedagogist for Contemporary Times. MAA Notes 1996, 40 (40), 291–302.

Valente, K. G. Giving Wings to Logic: Mary Everest Boole’s Propagation and Fulfilment of a Legacy. The British Journal for the History of Science 2010, 43 (1), 49–74.