2 Legos Furniture Optimization
James Kupetz; Earl Lee; Allison Marr; and Daphne Skipper
Problem 1:
Imagine that you are running a manufacturing business that makes tables and chairs out of Legos. The tables can be sold for $16 each and the chairs are sold for $10 each. Each table requires 2 big blocks and 2 little blocks while each chair requires 1 big block and 2 little blocks, as shown below. There are 12 big and 18 small blocks available to build tables and chairs.
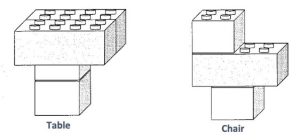
- What is the maximum revenue that you can achieve with these resources?
- How many tables would you build?
- How many chairs would you build?
- How do you know your solution is correct?
Solution
Students will likely begin by building 6 tables for a revenue of $96, because the revenue from a table is higher than the revenue from a chair. They will have some small blocks leftover and realize that they can take apart one table to build two chairs, increasing their revenue by $4. Doing this twice more leads to the optimal solution: 3 tables and 6 chairs for a revenue of $108.
Modeling the Legos Problem as a Linear Problem
The Legos problem can be modeled using a linear optimization model, or linear program, a name that is often shortened to “LP”. Linear programs have three main components: decision variables, an objective function, and constraints.
The decision variables in a linear program are variables that represent the decisions to be made. In this problem, we seek to determine how many tables and chairs to make. Thus, we define decision variables,
[latex]T=[/latex] the number of tables to make;
[latex]C=[/latex] the number of chairs to make.
Now we are ready to define our objective function: a function of the decision variables that represents the value that we wish to maximize or minimize. In this case, we wish to maximize revenue, which can be expressed as,
Maximize Revenue [latex]=16T+10C[/latex]
Finally, we must define the constraints, which are equations or inequalities that impose real world requirements on the values that the decision variables can take. In the Legos problem, we are restricted to using no more than 12 big and 18 small blocks. Each table requires 2 big blocks and each chair requires 1 big block, so we can express the number of big blocks that we use to make our furniture as . Thus, we can express the limit on the number of available big blocks as,
[latex]2T+C\le12[/latex]
Similarly, we can express the limit on the number of small blocks that are available for our furniture making as
[latex]2T+2C\le18[/latex]
The constraints limiting the number of available blocks are general constraints. Most linear programs also have variable bounds, which are a class of constraints that limit the range of the decision variables to a continuous interval of real numbers. In this case, it does not make sense to make a negative number of tables or chairs, so we add the so-called nonnegativity constraints,
T\ge0,C\ge0
Now we can write the linear program (LP) for the Legos problem:
Legos LP
Decision variables:
[latex]T=[/latex] the number of tables to make
[latex]C=[/latex] the number of chairs to make
Model
[latex]2T+2C\le18[/latex]
[latex]T\ge0[/latex]
[latex]C\ge0[/latex]
You may be thinking, “Don’t we also need to make whole numbers of tables and chairs?” This is true, of course. However, in addition to the objective function and constraints being linear, another requirement of a linear programming model is that the variables are allowed to take on any value in a continuous interval of real numbers (subject to the general constraints). A linear optimization model in which the variables are required to take on integer values is called an integer program (IP). Integer programs require a different, much more computationally expensive, algorithm. Thus, we allow fractional numbers of tables and chairs in our solutions.
The Legos model is a resource allocation linear program. Resource allocation problems typically seek to max-imize profit or revenue given limited production resources such as materials, manpower, or time. Resource allocation was one of the first applications of linear programming and is still commonly used in industry.
Here are a few resource allocation problems for modeling practice. Hint: Before writing the models for these problems, ask yourself the following questions:
- What are the decisions that need to be made in this problem? (Answering this question helps to define the decision variables.)
- What is the goal in the problem? (Answering this question helps to define the objective function.)
- What are the restricted resources? (This helps to define the constraints.)
Problem 2:
A manufacturing company can make devices using teams composed of 2 experienced engineers or 1 experienced engineer and three interns. Experienced teams build three devices every two hours, or 12 in an eight hour shift, while trainee teams build one device per hour, or eight in an eight hour shift. If the company has 12 engineers and 18 interns allocated to making devices, how many experienced teams and trainee teams should they use to maximize the number of devices constructed?
Solution
Let x be the number of engineer-only teams and let y be the number of training teams. The model is:
[latex]3y\le18[/latex]
[latex]x\ge0[/latex]
[latex]y\ge0[/latex]
Problem 3:
A company makes mp3 players to sell. They make two types of players, an economy player that sells for $45 and a higher-end player that sells for $65. The players are assembled from a battery and circuit components. One team creates the circuits and a second team makes the batteries and assembles the players. The economy model requires 1.5 worker hours for each battery and 2 worker hours for each circuit assembly. The higher end model requires 2 worker hours for each battery and 3 worker hours for each circuit assembly. In the battery assembly area there are 560 worker hours available and in the circuit assembly area there are 780 worker hours available. How many of each type of system should be built to maximize revenue?
Solution
Let x be the number of economy models produced and let y be the number of higher-end models produced. The model is:
[latex]2x+3y\le780[/latex]
[latex]x\ge0[/latex]
[latex]y\ge0[/latex]
