College of Science
109 Ant Empire: Mathematical Modeling of Supercolonial Invasions
Saya Zeleznik; Frederick R. Adler; and Patrick Talley
Faculty Mentor: Frederick R. Adler (School of Biological Sciences and Mathematics, University of Utah)
Background Information
Ant colonies are typically monodomous, composed of a single egg-laying queen and a labor force of sterile workers. Some species, however, are able to form supercolonies— interconnecting nests that maintain multiple queens— enabling them to spread across vast areas (“Supercolonies,” n.d.-d). This phenomenon is disproportionately represented among invasive ants, making them a major ecological threat by displacing native species (Holway et al. 2002, Ross et al. 1996). Understanding the mechanisms behind supercoloniality is therefore crucial for predicting and mitigating the spread of invasive species.
Supercoloniality is a common, but not universal strategy among invasive ants. For instance, Antwiki identifies only half of “highly invasive” species— those that are essentially or actually world-wide in distribution— as supercolonial. (“Invasive Ants,” n.d.-a; “Supercolonies,” n.d.-d; Table 1). This raises the question: what specific aspects of supercoloniality contribute to the success of invasive populations?
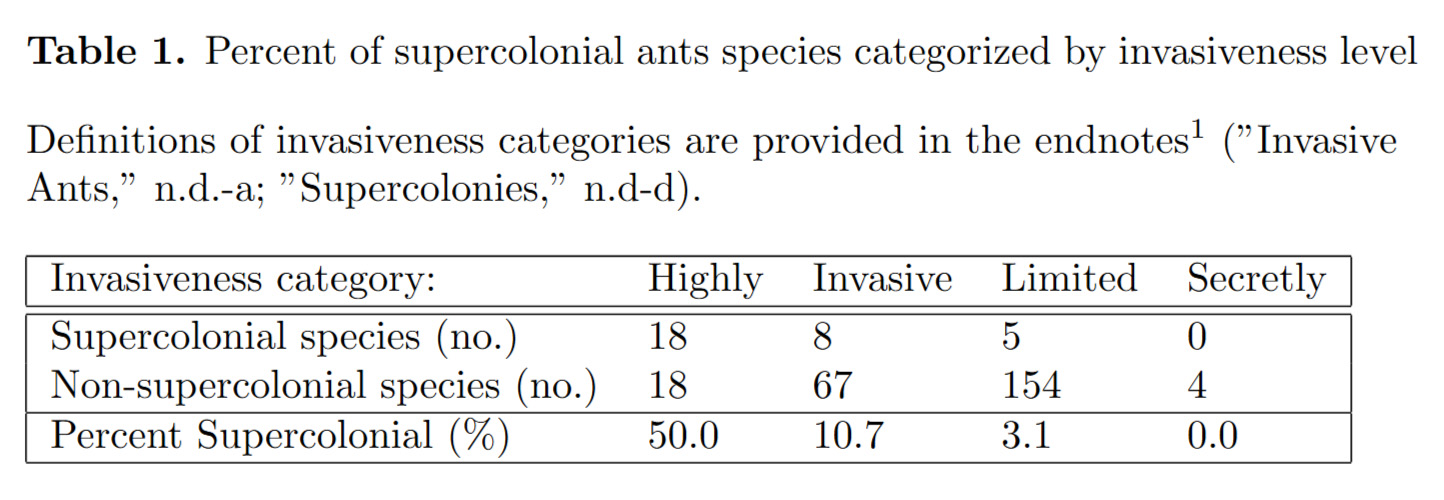
Supercoloniality hinges on polydomy— a colony structure in which two or more spatially separated nests function cooperatively, sharing resources and workers (“Polydomy,” n.d.-c; “Supercolonies,” n.d.-d). By examining the functional roles and evolutionary pressures that give rise to polydomy, we aim to better understand the basis of supercolonial organization. In this study, we examine how factors such as mass allocation, nest distribution, and the number and size of subnests influence the competitive advantage of polydomous ant colonies.
Addressing this question is scientifically, ecologically, and economically significant. Invasive ants rank among the most ecologically damaging species worldwide, with the red imported fire ant (Solenopsis invicta) alone costing the U.S. an estimated $1 billion in crop damage annually (Tsutsui & Suarez, 2003). Although controlling these species is both challenging and expensive, by understanding why invasive ants are able to succeed, we can aid ecologists in predicting, managing, and preventing their spread. Beyond conservation efforts, uncovering the organization of supercolonies also deepens our understanding of complex social organization and cooperation in biological systems. These insights even benefit cross-disciplinary research in areas such as computer science, where inspiration for algorithms is often drawn from ant behavior (Mullen et al., 2013).
Previous research proposes hypotheses that supercolonial behavior may arise in invasive ants due to increase in habitat saturation, genetic predisposition, or a decrease in intraspecies aggression at territory boundaries (Holway et al., 2002; Ross et al., 1996; Julian et al., 2002); our study investigates this third hypothesis, using mathematical modeling to simulate polydomous behavior.
We hypothesize that polydomous ant colonies tend to outcompete monodomous ants because of reduced allocation to colony defense, which may contribute to the success of invasive populations. Our study will test this by adapting Adler et al.’s (2018) mechanistic models of conflict to simulate territory disputes between a polydomous ant colony and monodomous competitors. By identifying when and why polydomy is beneficial, we hope to provide insight into the mechanisms that enable invasive ants to succeed in new environments.
Research methods
Our model is built on the “Scrum” model proposed in Adler et al. (2018); which measures the success of an ant colony via the shifts in territory boundaries at aras of conflict denoted the “scrum.” This model focuses on the ant allocation and the colony’s recruitment response to battles and territory gain, developed originally for the species Tetramorium (Adler et al., 2018). The model identifies seven different types of ants that occupy a given role in colony conflict dynamics. In our adaptation, we expanded this framework to allow ant types to travel bidirectionally from the nest, enabling a more realistic depiction of spatial dynamics (Figure 1).
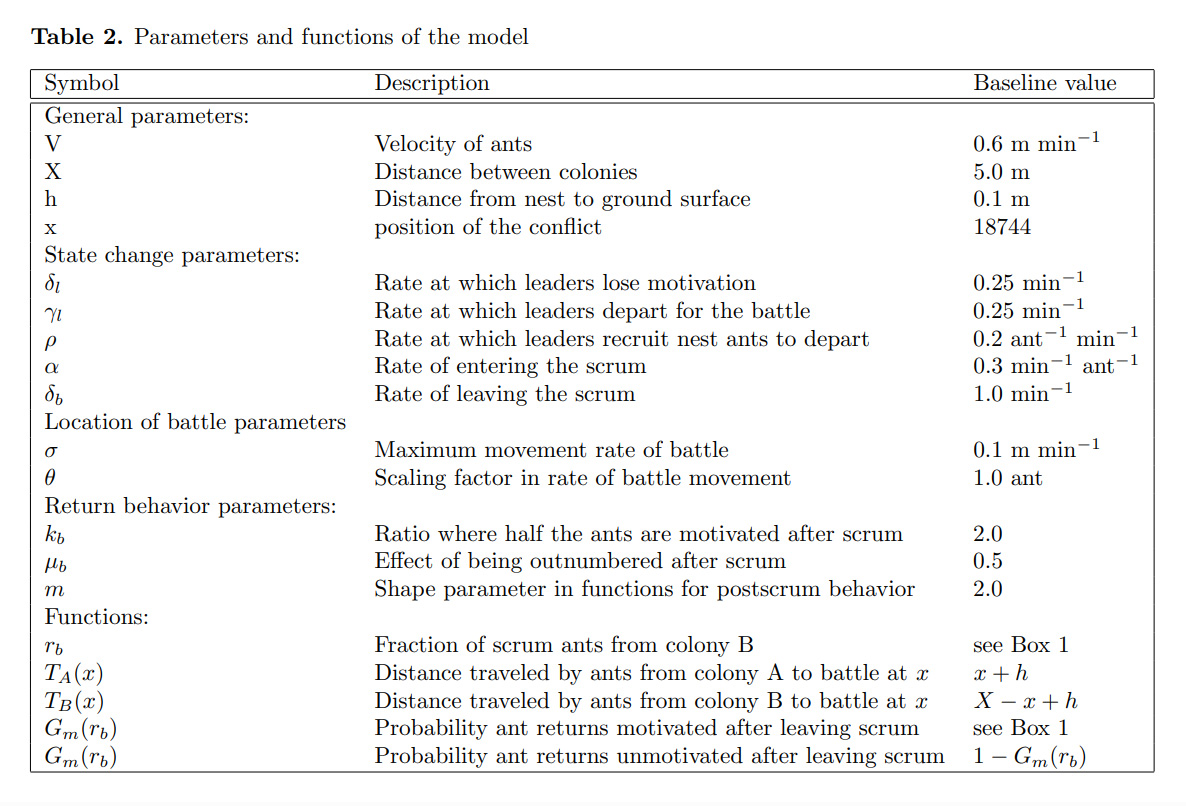
A system of differential equations is used to describe the movements and interactions of each ant type within a colony, as well as the movement of territory boundaries (Box 1). The third section of Box 1 describes the fraction of ants involved in the battle from an opposing colony, which is then used in the fourth section to calculate the likelihood that an ant returns to the nest either Motivated or Unmotivated. In our calculations, Colony A is placed at a reference point, x, while the other colonies are located at some distance on the landscape. The functions TA(x) and TB(x) are then used to calculate the distances colonies A and B must travel to reach the scrum, respectively (Box 1).
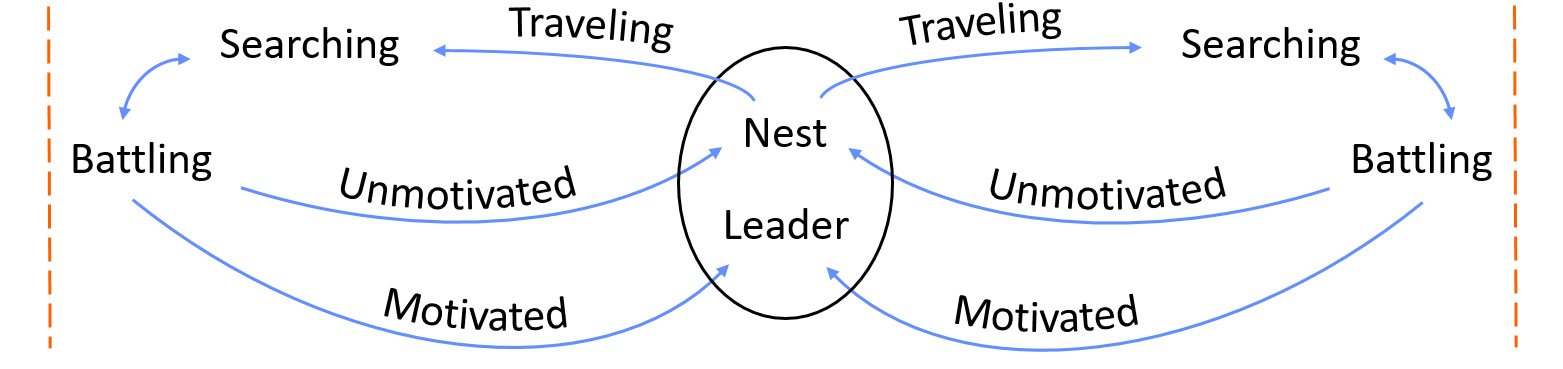
Figure 1. Ant types within a colony
oles within the colony are organized into different ant types. Nest ants spontaneously leave the nest and become Traveling ants that move towards the territory boundary, after which they become Searching ants that enter the scrum as Battling ants. The Battling ants then return to the nest in either a Motivated or Unmotivated state depending on the ratio of Battling ants from different colonies in the scrum (Box 1). The territory boundary then moves towards the nest with a smaller number of Battling ants (Adler et al., 2018).
We expanded the “Scrum” model further to encompass three ant colonies (A, B, and C) that inhabit a 1-D torus; this allowed for investigation of multi-directional conflicts (Figure 2). Our model, however, does not account for birth & death rates, food availability, or foraging behavior.
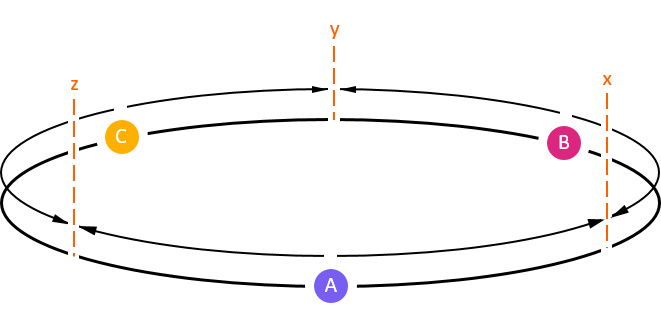
Figure 2. Colony placement on 1-D torus
Colony A (blue) fights with Colony B (pink) at territory boundary x, Colony B fights with Colony C (yellow) at territory boundary y, and Colony C fights with Colony A territory boundary z. Territory boundaries are denoted as vertical dashed lines.
In our experiment, the torus has a total length of 15 meters, with each of the three colonies assigned 5 meters of initial territory to control (Figure 2). Territory size for each colony is defined as the sum of the distances to the territory boundaries on either side.
To establish a control, we ran simulations in which all colonies exhibit monodomous behavior; each colony inhabited a single nest and was assigned the same biomass, measured in number of ants per colony. All colonies were placed in the center of their respective territories, with territory boundaries x, y, and z symmetrically located between them (Figure 2). As expected, the territory boundaries between the colonies remain static over time, indicating equilibrium under monodomous competition.
Next, we introduced polydomous behavior by dividing Colony A into N subnests such that total biomass was preserved: A1+A2+…+AN=B=C. In this model, the A subnests do not share nestmates or exchange information about the landscape. They do, however, recognize each other as members of the same colony and do not compete for territory among themselves. This colony structure represents a decrease in intraspecies aggression— a characteristic observed in many supercolonial species— and allows us to investigate how spatial organization affects territory size and control.
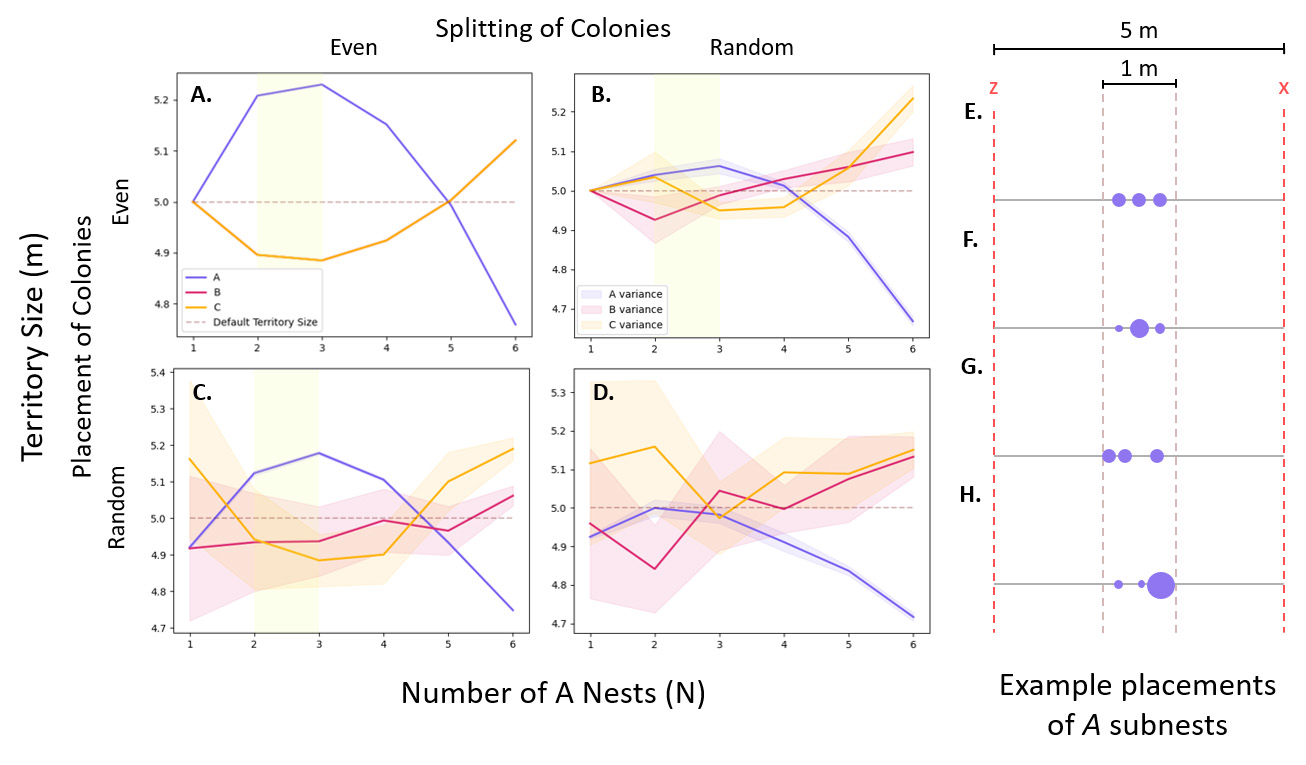
To investigate possible division strategies utilized by polydomous ants, we developed functions to split the biomass of A into randomly or evenly sized subnests, and functions to place these nests randomly or evenly within the A territory. We simulated each combination of splitting and placement strategies, and measured the effects on the territory size of Colonies A, B, and C as a function of the number of A subnests present (Figure 3A-D). For consistency, the A subnests were placed within 1 meter of the center of their territory for all strategies (Figure 3E-H).
For the even splitting and even placement of A nests (Figure 3A), the territory size of B and C are symmetric. This is a result of ordered placement on the 1-D torus— the changes in the territory size of A will have equal effects on the territory boundaries y and z, and therefore equal effects on colonies B and C, resulting in what appears to be only two lines in Figure 3A. For functions that involved randomness, we took the average over 20 trials to reduce noise (Figure 3B, C, and D). For the random splitting and even placement of A subnests in Figure 3B, biomass was distributed relatively uniformly across the landscape. In Figure 3D, however, random splitting and random placement led to uneven biomass distribution and increased variance in territory outcomes. Additionally, the variance in N=1 and N=2 in Figure 3D is attributed to random fluctuations and the inherent symmetry of the 1-D torus.
|
Results
We found that in most strategies, polydomous Colony A outcompetes monodomous colonies B and C when 2 ≤ N ≤ 3 (Figure 3A-C, highlighted in yellow). In contrast, Figure 3D shows that complete randomness does not result in territory gain for polydomous Colony A. This tells us that strategic organization, rather than multiple nests at random, contributes to the success of polydomy. With this in mind, we also see that when N > 4, polydomous Colony A does not show a competitive advantage against colonies B and C in any strategy (Figure 3A-D), indicating that sparsely spreading colony biomass over a large area does not incur an advantage to polydomous Colony A.
To further explore mechanisms that contribute to the success of A, we investigated the allocation of the different ant types when polydomous A is outcompeting monodomous colonies B and C. Specifically, we focused on the case of even splitting and even placement of A subnests when N=3 (Figure 4).
Figure 4 presents a matrix visualization of the allocation of each ant type within the three A subnests, and colonies B and C. Notably, when colonies B and C are losing territory to polydomous Colony A, they allocate substantially more biomass to Traveling ants at the shared y boundary (Figure 4, stars). This trend suggests that as A gains territory, it exerts territorial pressure on colonies B and C, forcing them to redirect their resources towards competing with each other.
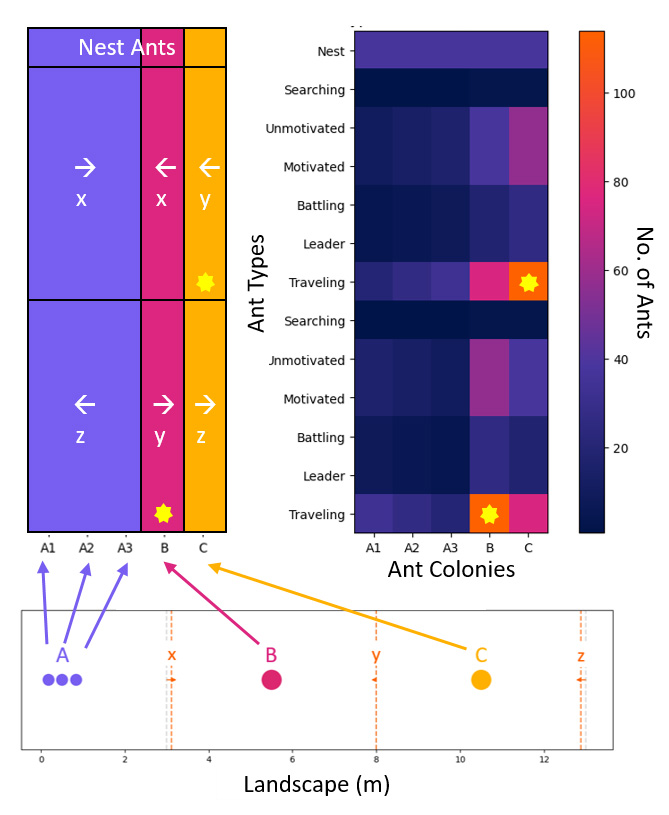
Figure 4. Ant type & allocation for N=3 When polydomous Colony A is gaining territory, monodomous colonies B and C are directing most of their biomass to the shared boundary, y, between them (yellow stars).
Interestingly, the number of Battling ants was lower than we had hypothesized. After revisiting the differential equations (Box 1), we identified two likely causes. First, from the values proposed in Adler et al. (2018) the rate of joining the scrum (ɑ) is notably less than the rate of leaving the scrum (δb), resulting in the net decrease in Battling ants over time (Table 2). Second, given the assigned velocity of ants, the distance to the battle results in a substantial delay in ant participation (Table 2). Together, these parameters likely account for the unexpectedly low number of ants in the Battling class
Following this, we explored the optimal ratio of dividing A subnests when polydomous Colony A outperforms monodomous colonies B and C. We first evaluated a strategy in which two A subnests were placed symmetrically within the A territory (Figure 5). In Figure 5, we see territory size of colonies A, B, and C, as a function of increasing splitting proportions (P). When P=0 all of A’s biomass is biased towards the x boundary, and when P=1, all of A’s biomass is biased towards the z boundary (right box). Our findings showed that when a small amount of biomass is allocated away from the main subnest (P≅0.15 or 0.95), A does not gain territory against colonies B or C. With two evenly divided A subnests, however, polydomous Colony A effectively outcompeted its monodomous competition.
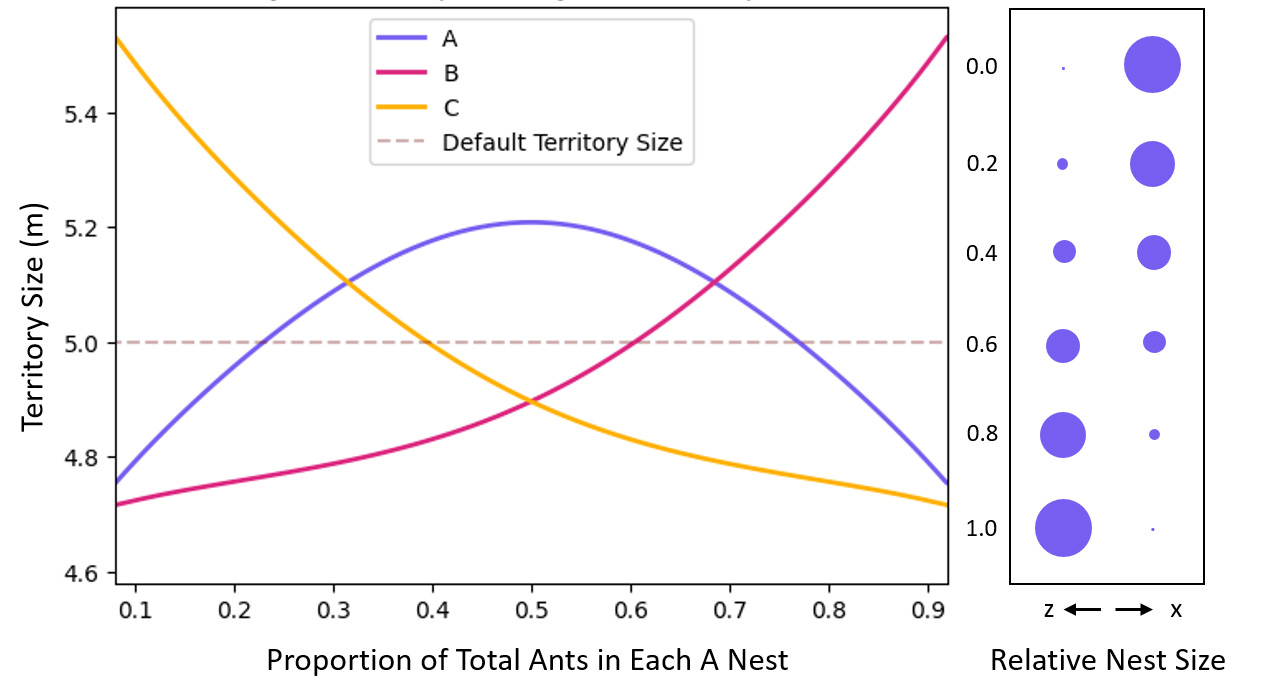
Figure 5. Territory size for different increasing proportions of A when N=2
When P=0.5 (A1 = A2), polydomous Colony A outcompetes monodomous colonies B and C.
We then examined the optimal placement of the two evenly divided A subnests within the territory and found that closer proximity to the x and z territory boundaries resulted in territorial gain against colonies B and C (results not shown).
Subsequently, we evaluated the optimal splitting of A subnests when N=3 (Figure 6). We observed that polydomous Colony A gained the most territory when the three subnests were nearly evenly split, or when the middle subnest received no biomass, concentrating resources towards the x and z territory boundaries.
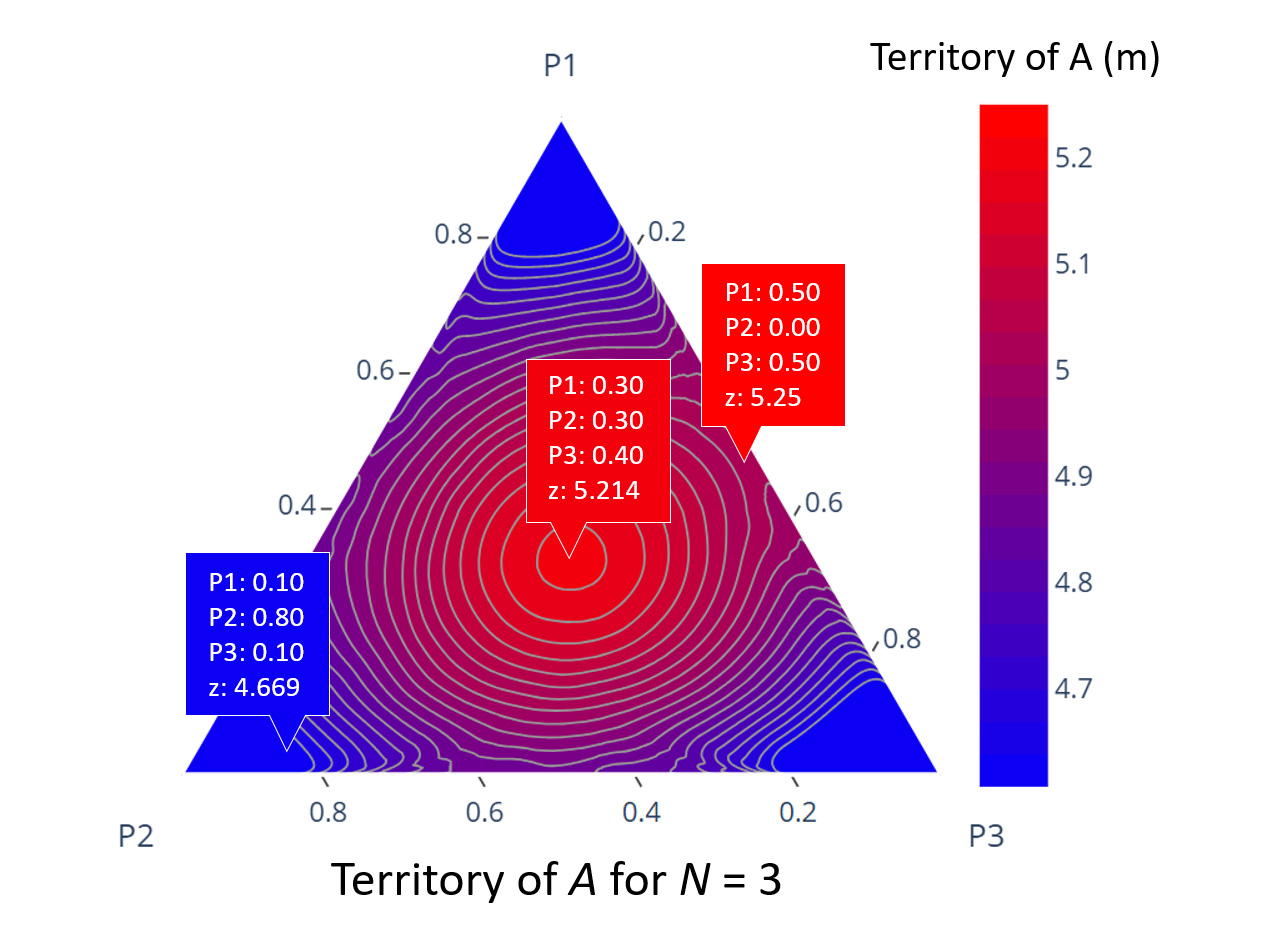
Figure 6. Territory of A when N=3
When polydomous Colony A is split into three evenly sized subnests, or two equally sized subnests placed close to competing colonies, they gained the most territory. P1 denotes the A subnest closest to the z boundary, while P3 denotes the A subnest closest to the x boundary. Territory size of polydomous Colony A is denoted as z.
These results suggest that polydomous Colony A does not benefit from allocating a small portion of biomass away from the main colony. In field studies of ant reproduction, this strategy aligns with dependent colony founding; specifically, reproduction by budding in L. humile, listed as one of the world’s top 100 most invasive species (“Linepithema humile”, n.d.-b). Furthermore, the advantageous placement of A subnests near the territory boundaries reflects behavior seen in invasive wood ants. In these species, certain nests are dedicated to foraging and are established close to resources, while other nests are located centrally and focused on reproduction (“Polydomy,” n.d.-c). Our model reflects these spatial and functional patterns of polydomy observed in real-world invasive ant species.
Polydomy is a key component of the strategy employed by supercolonial ant species. These ants maintain many interconnecting nests, each potentially housing multiple queens, which allows them to grow and spread quickly in new environments (“Supercolonies,” n.d.-d). By understanding the advantages of polydomy, we hope to shed light on why supercolonial ants are so effective as invasive ant species, and someday combat the effects they have on native environments.
Issues encountered
Initially, the model was implemented in R, which was sufficient for modeling monodomous conflict. When we tried to expand the model to include multiple subnets, however, we overwhelmed the computational capacity of the program. Although I was previously familiar with R in the context of coursework and research, transitioning to more advanced programming in a new language proved difficult. I noticed some similarities between R and Python, but the learning curve was steep given my limited programming background.
To continue the project, I also enrolled in additional math classes, including linear algebra, differential equations, and math biology. I applied the knowledge gained from these classes to the model in Python and although it slowed the project down initially, I now feel more prepared for real world analysis. While coding the model, the largest recurring issue was keeping matrix and vector shapes consistent between functions. This became especially challenging when calculating large sets of differential equations with various subfunctions. In the future, I will be more disciplined about noting the dimensions of each matrix & vector used in calculations in order to expedite troubleshooting in this area.
Main Findings
We found that polydomous colonies tend to do better than their monodomous counterparts when they evenly split into two or three groups within their territory, and establish their nests close to the territory boundaries. This pattern supports the idea that polydomy may contribute to the success of invasive supercolonial ant species.
Further Research
Simple additions to the current model would include adding noise or random perturbations in the initial placement of monodomous colonies B and C to more accurately simulate colony location. In the future, however, we would like to expand the model to two dimensions, add in foraging ants and food resources, add birth and death rates of the colony, and see how this affects ant allocation, territory size, and boundary movement.
Endnotes
1. Invasiveness categories are defined as follows:
- “Highly invasive” – species that are essentially or actually world-wide in distribution.
- “Invasive” – species that are very wide spread across multiple regions, but are not world-wide.
- “Limited Invasive” – species that occur at a limited number of sites outside their native range and often at low densities or with restricted distributions.
- “Secretly invasive” – species that occur outside their native range but in small numbers at low densities and often in non-disturbed habitats.
Bibliography
Adler, F. R., Quinonez, S., Plowes, N., & Adams, E. S. (2018). Mechanistic models of conflict between ant colonies and their consequences for territory scaling. The American Naturalist, 192(2), 204–216. https://doi.org/10.1086/698121
Holway, D. A., Lach, L., Suarez, A. V., Tsutsui, N. D., & Case, T. J. (2002). The causes and consequences of ant invasions. Annual Review of Ecology and Systematics, 33(1), 181–233. https://doi.org/10.1146/annurev.ecolsys.33.010802.150444
Invasive ants – antwiki. AntWiki. (n.d.-a). https://www.antwiki.org/wiki/Invasive_Ants
Julian, G. E., Fewell, J. H., Gadau, J., Johnson, R. A., & Larrabee, D. (2002). Genetic determination of the Queen caste in an ant hybrid zone. Proceedings of the National Academy of Sciences, 99(12),8157–8160. doi:10.1073/pnas.112222099
Linepithema humile – AntWiki. AntWiki. (n.d.-b). https://www.antwiki.org/wiki/Linepithema_humile
Mullen, R. J., Monekosso, D. N., & Remagnino, P. (2013). Ant algorithms for Image Feature
Extraction. Expert Systems with Applications, 40(11), 4315–4332. https://doi.org/10.1016/j.eswa.2013.01.020
Polydomy – AntWiki. AntWiki. (n.d.-c). https://www.antwiki.org/wiki/Polydomy
Ross, K. G., Vargo, E. L., & Keller, L. (1996). Social Evolution in a new environment: The case of introduced fire ants. Proceedings of the National Academy of Sciences, 93(7), 3021–3025.doi:10.1073/pnas.93.7.3021
Supercolonies. AntWiki. (n.d.-d). https://www.antwiki.org/wiki/Supercolonies
Tsutsui, N. D., & Suarez, A. V. (2003). The colony structure and population biology of invasive ants. Conservation Biology, 17(1), 48–58. doi:10.1046/j.1523-1739.2003.02018.x
