College of Science
103 Rationality of Spider Web Construction: Caloric Consideration
Madison Pearce; Andrej Cherkaev; Charles Godfrey; and Kaylee Pho
Faculty Mentor: Andrej Cherkaev (Mathematics, University of Utah)
Abstract
This paper offers insight into the delicate balance of spiders’ energy expense versus intake that their web achieves from a mathematical optimization perspective. Orb-weaver spiders build intricate and symmetrical webs that take a significant amount of energy to construct. This paper explores the caloric needs that a spider’s web demands and their effectiveness at catching prey under the physics and geometry constraints. By minimizing the caloric expense and maintaining effectiveness at catching prey one can optimize the ideal web for energy efficiency of a spider. We begin by exploring how an orb weaver constructs its web and the energy cost of each material in the web. Then we explore the caloric makeup that a spider has. Finally, we explore the calories spiders gain from catching prey. From there a mathematical model is created in two parts; calories out and calories in. The model incorporates constraints related to the nature of structural integrity and the biology of the spider. By using optimization techniques we are able to minimize the material cost and therefore energy of an orb weaver’s web.
Introduction
Spiders evolved from a species called trigonotarbids that roamed the earth nearly 400 million years ago [10]. Spiders did not always produce silk but through evolution evolved to produce silk to prevent eggs and prey from drying out. For roughly three hundred million years spiders were strictly ground living species, catching prey and living on the ground [10]. However, around 100 million years ago, insects started to evolve to have wings and this is when spiders evolved to build sticky webs higher up to catch prey. With this evolution came the earliest type of web to evolve called the orb webs [10]. The geometric design of the webs has not changed throughout much of evolution which shows its robust and optimized structure.
The previous research done on orb weaver spiders is limited in terms of energy calculations. There was some research done by zoologist Linden E. Higgins on weight gain of spiders and foraging habits [5]. Most of the research has to do with geometric properties of the web structure. This included research done in the Journal of Composites Science on angle between the radial threads and breakage patterns that occur when prey hits the web [8]. They found the angle to be between 11 and 14 degrees:
Figure 1. Unmeasured Spider Web (a) and Measured Spider Web (b) [8].
As well as the physical properties of spider silk have been studied extensively, and many of the factors, such as tensile strength, average density, and average weight have also been researched. Most parameters we used in the model were averaged out over large data sets, so they are seen to be representative of the real values.
The main purpose of this paper is to explore the caloric expense an orb weaver spider experiences while creating this orb web. The intention of investigating spider web optimization is to understand the effectiveness of spider webs while material and energy cost for the spider is minimal. As nature is economical and optimized this paper uses a reverse optimization technique. This means we assume spider web structure is already optimal and try to model the caloric needs it takes to build the web. With reverse optimization there can be multiple solutions depending on what is considered optimal and what constraints are applied to the system. Another thing to note is as this is a biological model it is by principle probabilistic. For this paper we assume prey size is hard to specify so it is assumed to be random.
Web-building Process of Orb Weaver Spiders
First, it is crucial to understand how a spider builds the web. The process of creating a web for an orb weaver species is very calculated and is done in the same process of steps each time. The first step in web making is to make the basic shape of the web starting with some anchor threads. As for the placement of these threads, it is still not fully understood how the spider decides where to put them. There are numerous hypotheses proposed by various researchers [12]. Once the anchors are in place the spider then makes the frame threads. The frame sets the size of the web and gives an idea of how wide the spider needs to go with their circular threads.
After the basic outline of the web is made with the anchor and frame the spider then goes in and starts creating radii threads. Radii threads are meant to give structure and rigidity and essentially anchor down the web. In addition to structure, these radii threads must be close enough so the spider can balance and walk on them to get to prey. The radii threads are created in a pattern that evens out the tension the structure experiences. For example, it will create a radial thread and then move to create the same radial thread in the opposite direction [12]. This way the tension is even in the web and there is not a point that is feeling more stress and potential to break at this stage in the process. After the spider creates this pair of radial threads it goes to the center of the web called the hub and tugs at all of the radial threads. By tugging the spider can tell where there is a lack of radii and fill in those gaps.
The last step is to create the capture threads. The spider moves in a spherical manner using all of its eight legs to hold onto the radii while moving along the web [12]. This creates a somewhat evenly spaced mesh-like structure. The silk used for spiral threads has a sticky adhesive applied to it while the spider is producing this section of the web [2].
This process is more or less the same for all orb weaver species, with some constraints and characteristics being unique to a species environment and evolutions [3], [4]. The basic structure for the spider web is shown in Figure 2.
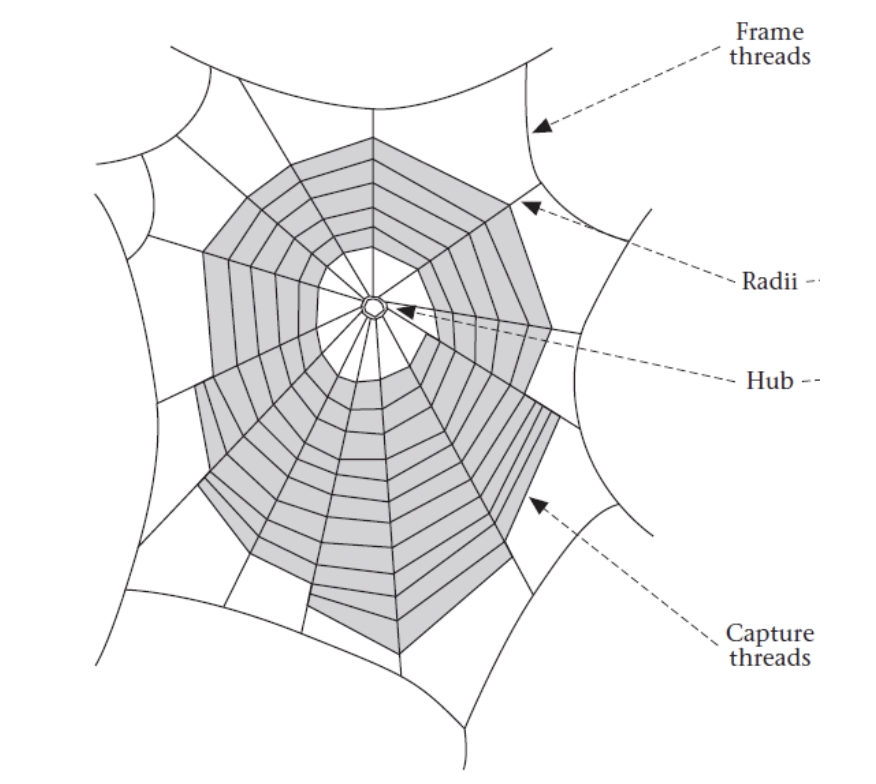
Figure 2. Typical orb weaver web showing types of threads and structure [11].
Assumptions in Model
Some generalizations such as average spider weight, weekly caloric intake, and certain environmental factors were assumed. These factors include inclement weather, availability of space to build the web, and a steady supply of possible prey. It was assumed because environmental factors influence webs equally and are subject to the principle of randomness, they may be discarded as constraints. Most orb weavers across different regions are subject to similar environmental constraints and all build web structures alike. This means that parameters like specific species, environment, weather, etc. were beyond the scope of the paper.
According to a source called Arachnoboards, the people who raise orbweavers in captivity claim the average orbweaver consumes an insect of similar size over the course of a week [1]. This amounts to anywhere between 10% and 25% of the spider’s body mass daily. In the calculations ahead, we use the same percentage of intake to body weight as a rough estimate of caloric intake required daily.
For example, an average orbweaver spider weighs around 80 mg, and has a caloric value of 50 calories [1], [6]. It therefore needs around 10 calories a week or 1.4 calories daily. Each gram of silk contains an average of 22.08 calories, and with the average web weight of .366 grams, each web contains about .02 calories. If we assume that it takes our spider five times the caloric capacity of the web to produce her web, we find the web requires 6-8% of it’s daily caloric intake to build. This means the spider needs to be consuming approximately .12 calories per day just to build a web.
Since all orb weaver spiders build similar web structures, and are of a similar size, we also took the parameter of spider size out of our model. Web size is proportional to the size of the spider so this parameter becomes a scalar value. With the basic model one can scale each equation to be larger or smaller to fit the type of spider they choose to focus on. This also makes constraining prey size easier as well, as there is a correlation between the size of the spider and the size of the prey it hunts.
From the research gathered, the main difference between radial threading and spiral threading is not a difference in silk type, more the adhesive material that covers the spiral threads. Because the main focus of this model is the radial angle between the radial threads, we’ve elected to add the extra caloric output required to produce the adhesive for the spiral threads to our list of assumptions. We think this is acceptable because it is a proportionality constant for each web, which is dependent on the total length of spiral webbing.
Other assumptions were made in narrowing down some parameters. Some of the bigger assumptions were:
- The spider will build its web in an area in which it will have a minimum population of prey.
- the caloric output needed to produce the silk for the radial threads.
- The caloric output needed to produce the adhesive for the spiral silk
- the daily caloric intake of an orbweaver
Model
We modeled energy in versus out accounting for calories. Our goal is not only to model minimized material cost of the web but also to capture the trade-offs involved in maintaining functionality for prey capture. This model considers both the energetic cost of silk production and the potential energy return from successful prey capture, providing a framework to evaluate different web designs in terms of efficiency.
To simplify the model of caloric expense of a spider web, we assumed a set of parameters. The
first two parameters being number of radial threads, 𝑛. By varying this parameter the web
becomes more or less dense. Similarly, the number of spiral threads, 𝑚, is another parameter affecting density. We also used two parameters 𝐶𝑠𝑝𝑖𝑟𝑎𝑙, 𝐶𝑟𝑎𝑑𝑖𝑎𝑙 for calories per silk type of spiral and radial threads respectively.
The first part of our model involves the energy required to build the spiral and radial threads in the web. We used the number of threads 𝑛 and took the length of those threads which is the
radius, 𝑟, of the web for the radial threads, and radial calories, 𝐶𝑟𝑎𝑑𝑖𝑎𝑙, required to produce the respective radial silk:
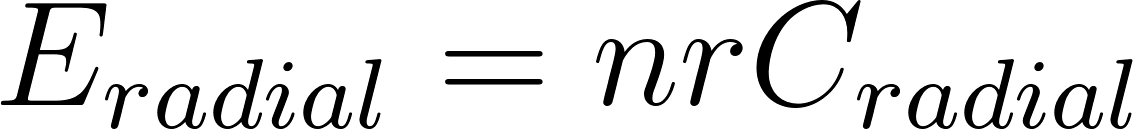
Then to find the energy required to make the spiral threads, we took the number of spiral threads 𝑚 and spiral calories, 𝐶𝑠𝑝𝑖𝑟𝑎𝑙, needed to produce the spiral type of silk. We represent the added calories required for the adhesive by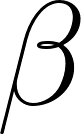 
. Note, this value will be some positive, non zero number. This becomes the first equations in the spider web energy model:
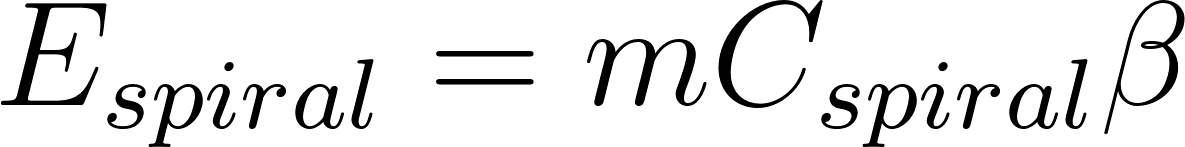
From here we can model the energy or calories needed to build the entire spider web:
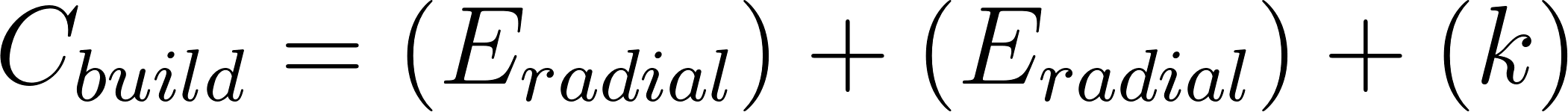
In this model, 𝑘 is some constant that represents the energy required to build frame, anchor
threads and the probability that the web will be destroyed and the spider will need to rebuild. For the purpose of simplification, we consider these amounts to be negligible as it is a smaller amount of energy compared to the total energy to build the web. Therefore, we neglect k because it is hard to determine due to the nature and randomness of building the frame and anchors.
Under the constraints listed below the effectiveness of the web is fixed meaning the web is optimal. This means the web uses minimal energy so should be modeled as:
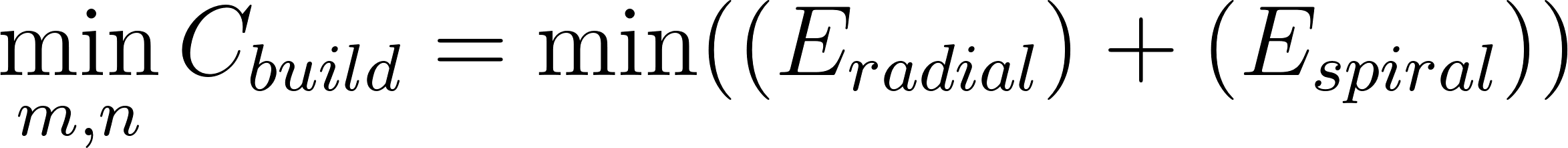
The second part of our model concerns the calories that the spider intakes from the web (ie. the prey caught in the web). Here we assume that with the increase in density, the web should be more effective as the mesh gets denser and flying insects have a higher likelihood of getting trapped in the web. To model the calories in, we used an area-based approximation. By this we can estimate the surface area that the threads take up in the total area of the web. First consider the silk length:
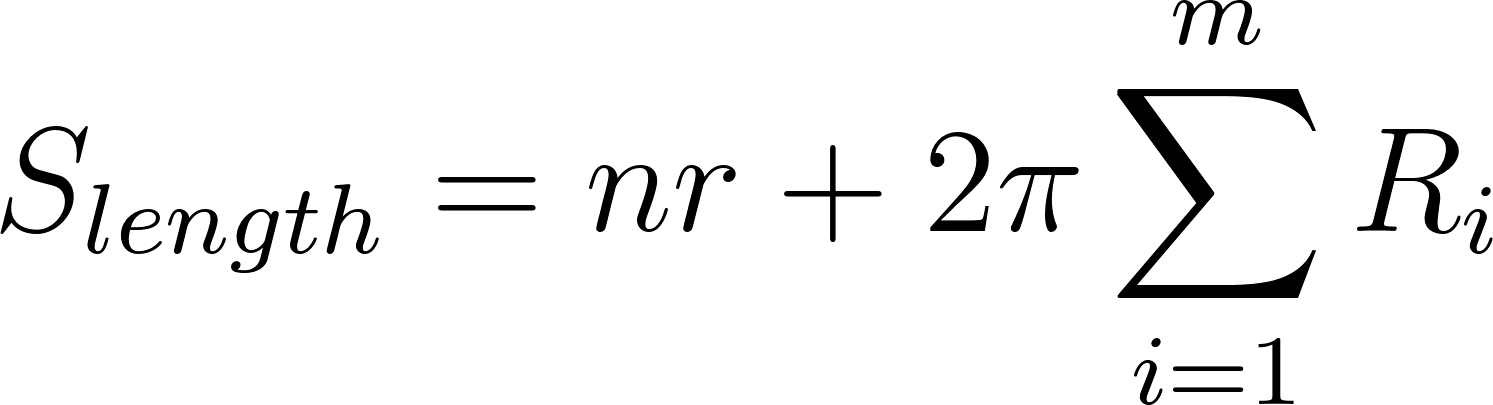
In this equation 𝑛 is the number of radial threads and the radius, 𝑟, of the spider web; resulting in the sum of the silk length used to make the radial threads. Then for the spiral threads, we take the number of spiral threads, 𝑚, and the circumference of the circle that the spiral threads create, 2π𝑅 where 𝑅 is the radius of the circle the spiral threads create.
From here we then model the entire area of the web if it were a dense disk:
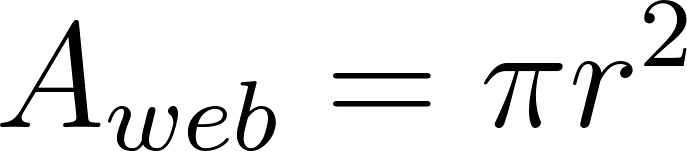
Using both of these equation we model the ratio of silk in the area of the web:
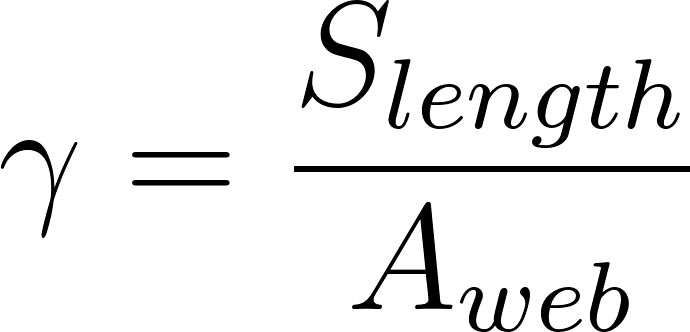
γ is essentially how much of the web is catching the prey. We also claim how many prey fly through the web and what the caloric value of that prey is. The number of prey that fly through a web depends on the environment. For the purpose of the model, we can represent this as a variable α. This α is a probabilistic value greater than 1, assuming the spider chooses a “prey rich” environment. The caloric value of prey depends on the size of the prey which is dependent on the size of the spider. We can represent this as 𝐶𝑝𝑟𝑒𝑦. Combining all of these aspects we can model the calories in as:
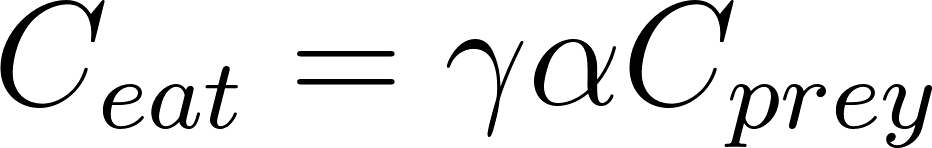
Now we have both calories in and calories out model so the total net energy is:
, 
The average orb weaver spider is about half an inch in size, and creates a web that’s 20 times its size in diameter, so the web is 10 inches in diameter. The area of the web is
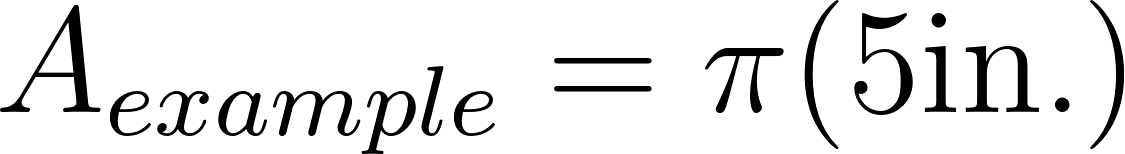
The length of silk that it produces, using n = 6, m = 4, and R = 2, 3, 4, 5 we find
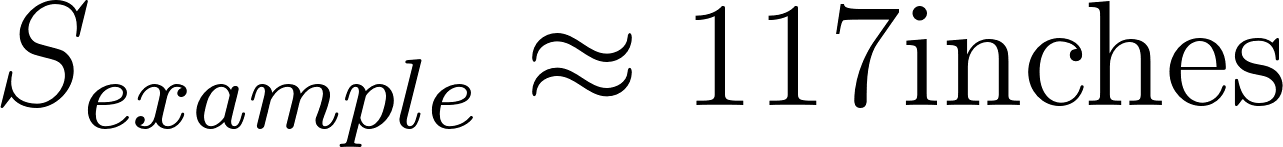
This leads to a gamma value of
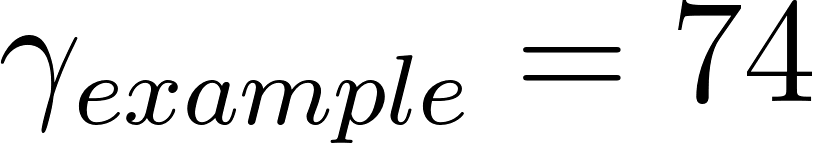
Physical Constraints
As a general rule we assume the spider keeps at least 20 percent of its total calories at all times. This accounts for keeping the spider alive and having the ability to reproduce. This net energyshould ideally be close to or greater than zero. This would mean that the spider is eating more than the calories they spent building the web. This would leave the spider in a position to have the energy to catch prey, fix the web in the case of damage or restart a new web. If the net energy were a negative number then this would mean the spider is spending more energy than it is intaking. This could mean the spider does not have enough energy to catch prey and therefore would not survive.
In order for the spider web to be functional and the model to be effective, we assumed a list of constraints. The constraints are in the form of inequalities as there is no set optimal number that is perfect for a spider web but rather certain thresholds or inequalities that need to hold when the web is minimized.
The first constraint to consider is:
This constraint makes sure that the energy gained from prey is greater than or equal to the calories spent to build the web. If this inequality is valued then the spider does not have enough energy to build the web or catch prey. This deems the web ineffective as it does not serve its purpose of catching prey to sustain the spider.
The next constraint follows that:
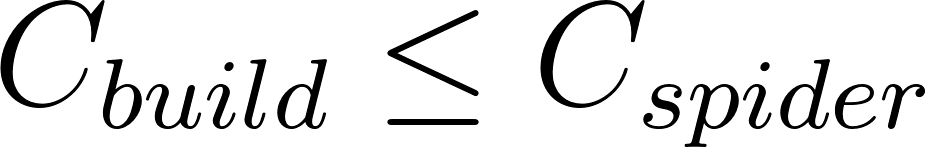
This constraint ensures that the spider has enough calories to begin with when the spider builds the web. If the calories required to build the web are bigger than what the spider can physically have, then the spider may die due to lack of energy. This constraint also controls the density of the web. If we strictly look at the effectiveness of a web to catch prey, then it makes sense that the more dense the web the more effective it is. However, this is not physically possible as the spider does not have enough energy to build a completely dense web with no gaps. This constraint controls the density of the web.
Geometric Constraints
The last constraints concern the structural integrity of the web. The structural constraints are:
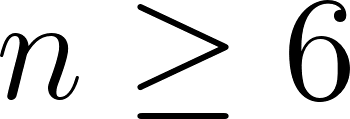
By having the number of radial threads be at least six, the web has structural stability and allows the spider to balance in the web. In reality, the number of radial threads is significantly higher but this is a lower bound to give structure to the web. It also should be an even number as the radial threads are created in equal and opposite direction to even out the tension in the web [12].
Lastly, if the web is too dense then the spider does not have the energy to build the web so it should not be so dense that it depletes the spider of all of its energy. On the other hand, if the web is not dense enough then prey can just fly through the gaps of the web between radial and spiral threads which means the web is not catching prey. This density condition means there can be a certain box of acceptable densities as there is not a set density that is the best. This range of density is dependent on prey size, the smaller prey the more dense the web should be and the bigger the prey the less dense it needs to be.
The Effectiveness of the Web
For our model, we want to preserve the effectiveness of the web with highly specialized structures designed to stop, trap, and hold prey. The web must absorb the kinetic energy of fast moving flying insects, such as flies and mosquitoes, without breaking or allowing the prey to escape [9]. Sticky spiral threads 𝑚 adhere to the insect on impact, while the radial threads 𝑛 provide structural support and absorb force. This dual function ensures the prey remains trapped until the spider arrives, enhancing the efficiency of the web without requiring the spider to expend additional energy in pursuit. From the energetic standpoint, a spider weighing 0.366 grams would spend approximately 112 calories to build a web which is about 18% of the energy it gained, corresponding to about 4-day building of a 20.6 cal/day [7]. However, for example, the average fly yields only 0.0067 cal upon consumption, so a spider must trap and consume approximately 14 such prey items to break even energetically. Given that orb-weavers often catch just 2-3 insects per web, they depend critically on the web’s mature spiral and radial threads to maximize capture success and minimize costly web replacements. Indeed, rebuilding an orb web can cost 7-15 times per spider’s daily maintenance energy, underscoring the value of durability. Resilient web architectures in optimizing net caloric gain.
To preserve the effectiveness of the orb web, our model integrates prey‐capture efficiency with mechanical resilience by explicitly accounting for silk material properties and architectural geometry. An orb web typically comprises 20–35 radial threads arranged at 10–15° intervals, overlaid by a spiral of capture threads spaced 2–10 mm apart to match local prey dimensions.
When an insect of mass 𝑀 and velocity 𝑣 collides with the web, its kinetic energy
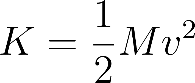
is converted into elastic potential energy
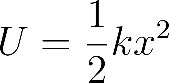
where k denotes the local stiffness of the silk (Young’s modulus ranging from 2 to 37 GPa) and 𝑥 the resulting deflection. Spider silk’s remarkable toughness, tensile strengths of 1,000–1,400 MPa and extensibility up to 30%, ensures that this energy transfer occurs without fiber failure. By optimizing the number and spacing of radial threads, spiders increase the stopping distance 𝑥, thereby reducing the average force on individual fibers
and preventing rupture. Anchor and frame threads further enhance compliance, effectively doubling the web’s overall energy absorption capacity under high‐impact conditions. The resulting radial–spiral network thus functions as a finely tuned safety net, sufficiently rigid to distribute and dissipate sudden loads, yet flexible enough to deform and recover, thereby maximizing prey retention, preserving the spider’s caloric investment in silk production, and minimizing the frequency of costly web reconstruction. This mixed with the physical and geometric constraints, the web is deemed effective.
Conclusion
This paper presents a mathematical model to explain the energy efficiency of the orb-weaver spider webs accounting for caloric expenditure and intake. By analyzing the process of web construction and the biological constraints of the spider, we saw that an orb weaver spider balances material use while preserving web effectiveness. Our model offers insight into the complex interplay between mathematics and physics that allows spiders to maximize their survival with minimal energy waste. Through defined constraints and key assumptions, we show how orb weavers can maintain structural integrity and prey capture efficiency within their limited caloric budget. Therefore, this work may help us deepen our understanding of natural “engineering” and model the energy a spider takes to build the web.
Future Research
There are some directions we would like to continue research, namely, expanding the model based on continuous membrane mechanics. This could include accounting for the kinetic and elastic potentials that the web experiences as a result of catching prey or similar issues with force dynamics. This is a valid avenue of research, although it is currently out of the scope of this paper.
Some other areas to look into are the environmental factors (weather, economical principle of nature, etc.) that affect web development, as this study made some generalizations regarding specific factors. One area of particular interest is to investigate whether the findings regarding web optimization carry over from different species of spider, or if the optimization changes mostly on environmental factors.
Acknowledgments
Special thanks to Andrej V. Cherkaev for the mentoring, and to the NSF for funding through the RTG award (NSF DMS-2136198).
References
[1] Arachnoboards, Orb Weaver feeding, n.d. [Online]. Available: https://arachnoboards.com/threads/orb-weaver-feeding.339663/
[2] Forest Preserve District of Will County, Nature Curiosity: Why Is Spider Silk Sticky?, Sep. 9, 2022. [Online]. Available: https://www.reconnectwithnature.org/news-events/the-buzz/nature-curiosity-why-is-spider-silk-sticky/
[3] Harmer, A. M. T., Blackledge, T. A., Madin, J. S., and Herberstein, M. E., “High-performance spider webs: integrating biomechanics, ecology and behaviour,” J. R. Soc. Interface, vol. 8, pp. 457–471, 2011. doi: 10.1098/rsif.2010.0454.
[4] Herberstein, M. E. and Tso, I.-M., “Evaluation of formulae to estimate the capture area and mesh height of orb webs (Araneoidea, Araneae),” J. Arachnol., vol. 28, no. 2, pp. 180–184, 2000. [Online]. Available: http://www.jstor.org/stable/3706020
[5] Higgins, L. E., “Direct evidence for trade-offs between foraging and growth in a juvenile spider,” J. Arachnol., vol. 23, no. 1, pp. 37–43, 1995. [Online]. Available: http://www.jstor.org/stable/3705908
[6] Porter, D., Vollrath, F., and Shao, Z., “Predicting the mechanical properties of spider silk as a model nanostructured polymer,” Eur. Phys. J. E, vol. 16, no. 2, pp. 199–206, 2005. doi: 10.1140/epje/e2005-00021-2.
[7] Prestwich, K. N., “The energetics of web-building in spiders,” Comp. Biochem. Physiol. A Physiol., vol. 57, no. 3, pp. 321–326, 1977.
[8] Regassa, Y., Lemu, H. G., Sirabizuh, B., and Rahimeto, S., “Studies on the geometrical design of spider webs for reinforced composite structures,” J. Compos. Sci., vol. 5, no. 2, p. 57, 2021. doi: 10.3390/jcs5020057.
[9] Walker, J., “What do orb webs catch?” Bull. Br. Arachnol. Soc., vol. 9, no. 3, pp. 95–98, 1992. [Online]. Available: https://britishspiders.org.uk/system/files/library/090303.pdf
[10] Welton, R. K., “Spider Evolution – 3d Trigonotarbid and the Spiders from Tars,” The Bristol Dinosaur Project, Nov. 17, 2020. [Online]. Available: https://dinoproject.blogs.bristol.ac.uk/2020/11/17/rachel-spiders/
[11] Wijerathna, T., “An investigation of the variations in morphometry and the web architecture of the giant wood spider (Nephila pilipes) in forest and non-forest habitats in the Wet Zone of Sri Lanka,” 2016. doi: 10.13140/RG.2.2.35074.27846.
[12] Zschokke, S., “Early stages of orb web construction in Araneus diadematus Clerck,” Rev. Suisse Zool., vol. 2, pp. 709–720, 1996. [Online]. Available: https://bio.staern.li/pdf/zschokke1996rsz.pdf
