John and Marcia Price College of Engineering
29 The Effect of Lung Tumor Outgrowth on Strain Distributions in Nearby Alveolar Walls
Sylvia Pack; Jeffrey Weiss; Michael Herron; and Steven Labelle
Faculty Mentor: Jeffrey Weiss (Biomedical Engineering, University of Utah)
Introduction
Lung cancer is the leading cause of cancerous death in the United States.1 New screening methods have been developed aiming to catch pre-cancer, but 23% of patients suffer a local recurrence within 5 years.2 Lung tumors are unique in that they develop within soft tissue that is under regular cyclical mechanical stretch due to normal respiration. Stretching of lung epithelial cells adjacent to the tumor tissue border has been connected to early-stage lung tumor growth.3 These cells fill the alveolar space and thicken alveolar walls, which causes the extracellular matrix (ECM) peripheral to the tumor to deform4. This ECM displacement is associated with tumor stiffening, an established tumor progression driver, but the contribution of strain to lung cancer is unknown.5 The contribution of strain to the growth of early lung cancer is difficult to study solely via experiments. Earlier reports have concluded that alveoli at the edge of lung tumors experience amplified strain during respiration.7
Therefore, this observation led to the investigation into strain inducing activation of tumor growth signaling at the tumor edge, thereby increasing the area of amplified strain during respiration. We tested the hypothesis that circumferential tensile strain at the edges of growing tumors may be large enough to cause alveolar wall failure and early tumor spread. Determining the contribution of strain to alveolar wall failure has the potential to uncover principles that predict adenoma progression to deadly cancer.
Methods
Material assignment
The foundation of the FE models was established in a preliminary study.7 These models consist of a hexagonal lattice, to represent the alveolar network, and solid tumor (Figure 1.A). The hexagonal lattice was made from a MATLAB (www.mathworks.com) script that created a mesh of uniform hexagonal shapes; then to account for variability in the lung, a randomized algorithm was applied to the idealized hexagonal lattice. The thickness of the walls was chosen to be 30 m.8
The material was classified as elastic neo-Hookean, which is typical for elastic biological tissue9. Based on experimental data, the lung lattice had a Young’s Modulus of 3.5*10-8 (Pa) and a Poisson ratio of 0.25. A tumor was constructed from this lattice through the selection of 20 alveolar spaces in a cluster with the material properties of a solid tumor. The tumor is classified as neo-Hookean with a Young’s Modulus of 3.5*10-8 (Pa) and a Poisson ratio of 0, indicating no lateral deformation in the tumor when stretched or compressed. All FE models were established and analyzed in FEBio (www.febio.org).
Prestrain
In order to simulate strain in the lung due to respiration, prestrain was implemented. Prestrain is the applied strain before the growth of the tumor, which was used to simulate the strain experienced in the alveolar walls during respiration. To represent inhalation, the lattice edges were displaced to produce 20% global elongation, while for exhalation, it was displaced 5%.10 The entire model was constrained to have zero displacement in the Z-direction, simulating plane strain conditions. A single row of nodes was selected from the top and bottom of the edge of the normal lung lattice, and a single column of nodes was selected from the left and the right sides at the edge of the normal lung lattice. These selections were given a prescribed displacement, representing inhalation and exhalation, in the y-direction and x-direction. Two models were made: one with a prestrain value of 5% (exhalation) and the other with a prestrain value of 20% (inhalation). FEBio is run according to a time scale, so this prestrain was applied from time 0-0.5 and the tumor growth was applied from time 0.5-1.
Tumor Growth
The tumor growth was simulated through a feature in FEBio known as active contraction, specifically transversely isotropic active contraction. This mechanism involves the parameter of prescribed stress, which in this research was tumor growth, a value of -1.6*10-9(Pa) was set. An active contraction value when negative will cause the material to expand instead of contract. The value set for tumor growth was established in an earlier model that allowed for complete convergence when running the simulation.
Postprocessing
Once the models ran to completion, a Python (www.python.org) script was developed that would deliver an output of two pieces of information from the plot file. The first was the average 1st principal Green-Lagrange strain found in each ring of alveolar wall after tumor growth. These ‘rings’ are concentric to the tumor and were calculated according to the tumor coordinate center. The script contained a search threshold of 45 degrees to avoid non-circumferentially oriented alveolar walls. Strain was calculated across 6 rings with 100 m spacing between each. Once the element set for each ring had been established, the strain value was averaged for each ring. The second output from the script was the distance of each ring according to the tumor edge. This was calculated by finding the radius of the tumor at the last timestep, as the script had already utilized the center of the tumor for ring calculation, and the distance to the center of the tumor to each ring. Therefore, the distance from each ring to the edge of the tumor was calculated by subtracting the two numbers.
Graphs were constructed in Origin Pro 2024 (www.originlab.com).
Results
The results clearly demonstrated rotation and stretching of alveolar walls near the tumor. The highest 1st principal strain values were found in the alveolar walls near the tumor (Figure 1.B).

AB
Figure 1.A. 2D Lung and Tumor Model. The tumor is located in the middle of the figure (grey) and consists of a cluster of 20 filled alveolar spaces. The lung lattice surrounds the tumor (blue) in a randomized hexagonal pattern. Figure 1.B. Post Tumor
Growth Strain Distribution
Model after 20% prestrain and tumor growth. There is an increase of the 1st principal strain in the alveolar walls near the tumor edge.
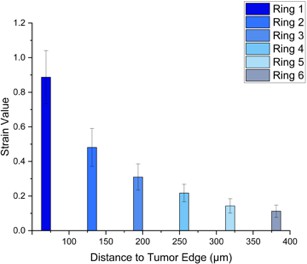
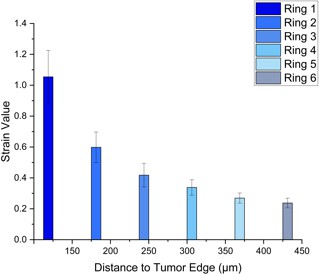
The model with 5% applied strain (Figure 2.A) had 6 rings. Ring 1 (5%) had an average strain value of 0.8871, and an average distance of 54.16 m to the tumor edge after growth. Ring 6 (5%) had an average strain value of 0.11276, and an average distance of 369.9 m to the edge of the tumor. The model with 20% applied strain (Figure 2.B) also had 6 rings. Ring 1 (20%) had an average strain value of 1.054 and an average distance of 50.02 m to the tumor edge. Ring 6 (20%) had an average strain value of 0.2374 and an average distance of 454.3 m to the tumor edge. Overall, as distance from the tumor after growth increased, the strain in the alveolar walls decreased. The tumor had a constant growth rate for both models but had different relative volumes in tumor size. The 5% model had an average volume change of 5.733 time the original tumor size, while the 20% model had an average relative volume change of 6.560.
A
B
C
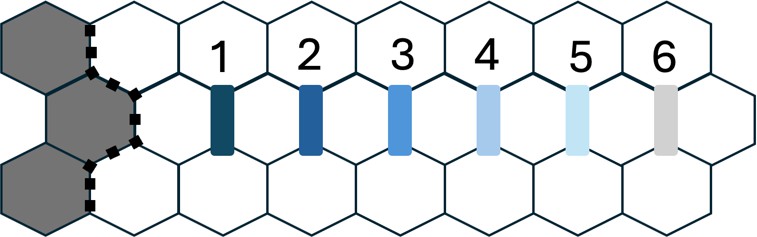
Figure 2.A. 5% Applied Strain. Depicts the average strain value, after 5% prestrain and tumor growth, in the alveolar network dictated through rings with an increase of 100 m from the tumor edge reaching a total of 6 rings. Figure 2.B. 20% Applied Strain. Depicts the average strain value, after 20% prestrain and tumor growth, in the alveolar network dictated through rings with an increase of 100 m from the tumor edge reaching a total of 6 rings. Figure 2.C. Ring Map. Schematic indicating the rings centric to the tumor in the alveolar network.
Discussion
There was an increased area of amplified strain during respiration, specifically inhalation. This is to be expected as the alveolar walls experience a greater change in length (strain) during inhalation compared to exhalation. The 1st principal strain values experienced by the alveolar walls due to simulated tumor outgrowth were as high as 100%, which based on data from the literature, are large enough to cause failure of the alveolar walls. This could lead to tumor outgrowth into adjacent alveolar spaces. The relative volume was greater in the 20%
Lung cancer remains the leading cause of cancerous death in the United States1, making lung cancer research essential for medical progression. A significant implication of this research is the potential for mechanical strain to serve as a biomarker for early lung cancer progression. These mechanics developed in the lung models could be used toward predictive modeling, involving the image of early lung tumors being modeled using these mechanisms to predict specific tumors likelihood of metastasis. This could offer a world altering method and would change the treatment of tumors.
Bibliography
- R. L. Siegel, et al., CA Cancer J Clin, vol. 74, no. 1, pp. 12–49, 2024.
- A. H. Krist, et al., JAMA, vol. 325, no. 10, pp. 962–970, 2021.
- C. M. Waters et al., Compr Physiol, vol. 2, pp. 1–29, 2012.
- I. Jorba et al., Acta Biomater, vol. 92, pp. 265–276, 2019.
- J. L. Leight, et al., Annu Rev Cancer Biol, vol. 1, pp. 313–334, 2017
- S. P. Reese, et al., Biomech Model Mechanobiol, vol. 12, no. 6, pp. 1195–1204, 2013.
- R. G. Zitnay et a., PLoS Comput Biol, vol. 18, no. 10, Oct. 2022.
- H. Fukaya, et al., J. Appl. Physiol., vol. 25, no. 6, pp. 689–695, 1968.
- A. M. Birzle, et al., J Mech Behav Biomed Mater, vol. 94, no. January, pp. 126–143, 2019.
- G. Burgstaller, et al., Euro Resp J, vol. 50, no. 1, 2017

