Faculty Mentor: Blair Sullivan (School of Computing, University of Utah)

Introduction

Robotics has become an essential tool for a diverse range of fields, enhancing the precision and efficiency of tasks in areas such as industrial automation, infrastructure monitoring, and medical procedures. A critical challenge to these applications is inspection planning, the development of a motion plan for sensing a series of points of interest, POIs. This problem, which holds an essential role in robotic automation, is computationally intensive, known to be PSPACE-hard [1], as the addition of points of interest results in the exponential growth of the search space. This growth constitutes an obstacle to real-time applications, especially in surgical situations where fast computations are crucial, making naive solutions, such as exhaustive search or sequential visits, unattainable. Furthermore, simply collecting the points is not sufficient, as constraints prioritize the most efficient path, where the shortest route is wielded while ensuring maximum coverage of the POIs in space. In this project, we introduce two algorithms for solving the inspection problem exactly and optimally, denoted ILP-IPA and DP-IPA [6].

Methods

We conceptualize inspection planning as a graph problem, modeling a robot’s motion plan as a closed walk in an edge-weighted graph. In this configuration, POIs are represented as color sets associated with vertices, and the goal is a walk that minimizes transition costs while maximizing the number of inspected POIs. Building on IRIS-CLI [2], which iteratively constructs a rapidly-exploring random graph (RRG) to represent robot configurations, with vertices labeled by inspectable POIs and edges weighted by transition costs, we enhance the computation of the inspection path by applying fixed-parameter tractability (FPT) [3] within a dynamic programming approach (DP), solving efficiently in both memory and space.

Additionally, we propose a novel Integer Linear Programming (ILP) formulation inspired by flow-based techniques for optimization [4]. To manage the exponential complexity of large instances, we employ two graph simplification strategies: color reduction and walk merging. In color reduction, a greedy max-dispersion algorithm [5] selects a smaller, diverse subset of representative POIs, reducing computational demands while preserving problem diversity.

Walk merging then addresses smaller, color-reduced subproblems, integrating the resulting paths into a single, coherent route to minimize overlaps and redundancies. These strategies enable our approach to scale effectively, maintaining high coverage and optimality while achieving practical efficiency for real-world applications.

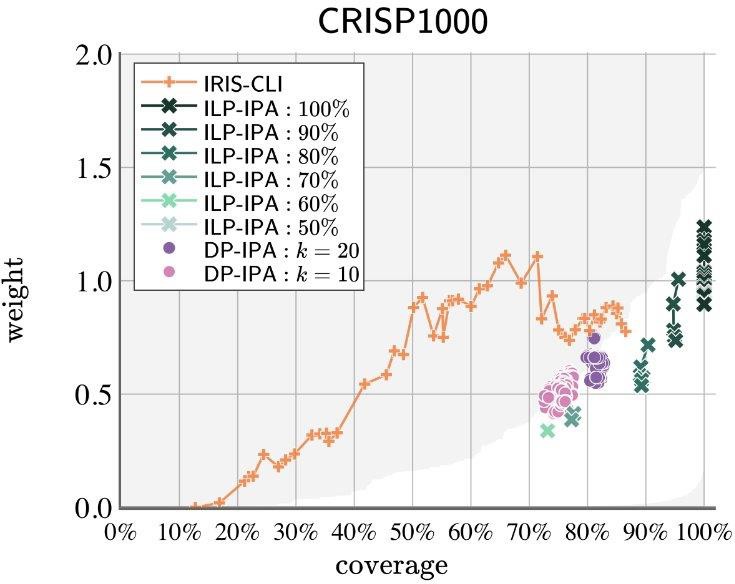
Figure 1. Performance of IRIS-CLI, ILP-IPA and DP-IPA on CRISP and DRONE datasets.

Results

To assess the practicality of our proposed algorithms, we ran extensive experiments on two real-world representative instances, CRISP and DRONE, originating from a pleural cavity inspection scenario and a bridge inspection plan, respectively. In terms of efficiency, ILP-IPA achieved a 30% reduction in path weight while maintaining or improving coverage compared to IRIS-CLI and provided solutions that inspected all POIs with only 16% more weight. In terms of coverage, DP-IPA outperformed IRIS-CLI, achieving 68% coverage compared to IRIS-CLI’s 64%, while also reducing path weight by more than 50%. ILP-IPA showed significant improvements in smaller instances, delivering higher coverage with lighter solutions. For larger graphs, DP-IPA outperformed IRIS-CLI with lower solution weights and strong coverage, remaining effective even when ILP-IPA timed out. While ILP-IPA excels in smaller instances with optimal, high-coverage solutions, it struggles with larger graphs due to complexity. Together, DP-IPA and ILP-IPA provide complementary strengths for different problem sizes, making them practical solvers for real-world inspection tasks.

Conclusion

In this project, we introduced two algorithms, ILP-IPA and DP-IPA, to address the computationally intensive problem of robotic inspection planning, leveraging fixed-parameter tractability and simplifications such as POI reduction and walk merging. These strategies enabled our algorithms to outperform the state-of-the-art IRIS-CLI, with ILP-IPA excelling in smaller instances with higher coverage and lower path weights, and DP-IPA demonstrating robust scalability for larger graphs. The integration of POI reduction techniques proved critical for improving efficiency while maintaining significant coverage. Our future work will focus on deploying these algorithms on prototype robots, exploring advanced reduction methods, and further research on novel algorithms for tackling robotics motion problems.

Bibliography

Halperin, D., Salzman, O., Sharir, M.: Algorithmic Motion Planning. In: Handbook of Discrete and Computational Geometry. Chapman and Hall/CRC, 3rd edn. (2017).

Fu, M., Salzman, O., Alterovitz, R.: Computationally-efficient roadmap-based inspection planning via incremental lazy search. In: 2021 IEEE International Conference on Robotics and Automation (ICRA), pp. 7449–7456. IEEE (2021).

Fomin, F.V., Golovach, P.A., Korhonen, T., Simonov, K., Stamoulis, G.: Fixed-Parameter Tractability of Maximum Colored Path and Beyond. In: Proceedings of the 2023 Annual ACM-SIAM Symposium on Discrete Algorithms (SODA), pp. 3700–3712. Society for Industrial and Applied Mathematics (Jan 2023).

Cohen, N.: Several Graph Problems and Their Linear Program Formulations. Research Report, INRIA (2019).

Gonzalez, T.F.: Clustering to Minimize the Maximum Intercluster Distance. Theoretical Computer Science 38, 293–306 (1985).

Mizutani, Y., Salomao, D.C., Crane, A., Bentert, M., Grønås Drange, P., Reidl, F., Kuntz, A., Sullivan, B.D.: Leveraging Fixed

Parameter Tractability for Robot Inspection Planning. In: The 16th International Workshop on the Algorithmic Foundations of Robotics (WAFR) (2024).