The Equilibrium (Nernst) Potential
Dentyn Sacre and Jim Hutchins
Chapter under construction. This is the first draft. If you have questions, or want to help in the writing or editing process, please contact hutchins.jim@gmail.com.
For ions to travel across the cell membrane and change the cell potential, either toward or away from the action potential threshold, two things must be present. First, ions must have access to an open channel; and second, there must be a force driving the movement of ions either into or out of the neuron.
One force is the natural diffusion of ions from places of high concentration to lower concentration. Similar to how a spray of perfume will eventually lead to those fragrant particles spreading throughout a room, so do aqueous ions dissipate throughout a solution. This dissipation, otherwise known as diffusional flux, is guided by a process identified in the second law of thermodynamics: that a difference in concentration causes a concentration gradient, driving particles to spread out and eliminate such differences and restore a state of equilibrium. If this state of equilibrium is reached, the result is no concentration gradient to drive particle movement.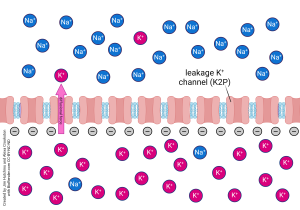
A cell only permeable to K+ is experiencing an efflux of potassium ions due to the presence of open potassium leakage channels and a concentration gradient driving movement outward.
The other force is electrostatic, based on the relationship of attraction between particles of opposite charges and repulsion between particles of like charges. The movement of particles due to these forces is called electrical flux, and can drive ions to move into or out of the cell, resulting in cell potential, which is measured by finding the difference between the voltage inside and outside of the cell.
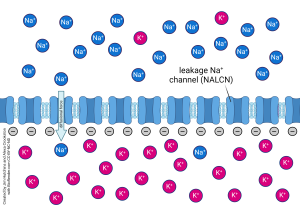 A cell only permeable to Na+ experiences an influx of sodium ions due to the presence of sodium leakage channels and electrostatic attraction of cations such as Na+ to the negatively charged cytosol.
A cell only permeable to Na+ experiences an influx of sodium ions due to the presence of sodium leakage channels and electrostatic attraction of cations such as Na+ to the negatively charged cytosol.
Diffusional and electrostatic forces work with or against each other to govern the movement of ions into or out of cells. When in opposition, there exists a point of equilibrium between cell potential and the concentration gradient where the movement of a particular ion into and out of the cell is equivalent.
Building on Fick’s first law, which is an equation describing the relationship between diffusion and the concentration gradient of a particle, and Einstein's relation equation, which connects the diffusion coefficient outlined in Fick's first law with particle mobility in the presence of electrical fields, the Nernst potential is used to better understand the nature of ionic movement across the neuronal membrane.
In Fick's first law, the diffusion coefficient is used to express the rate that particles can spread from places of higher to lower concentration in a medium. Einstein's relation uses mobility to refer to how easily particles can travel through a medium as facilitated by an electrical force, such as a charge. Combining these equations clarifies how a particle, such as an ion, moves in environments where both diffusional and electrical forces are present.
The Nernst (equilibrium) potential is used to calculate the difference in electrical potential across a cell membrane when the movement of a particular ion is in thermodynamic equilibrium, assuming the cell is only permeable to that ion. In other words, the cell potential needed to oppose the movement of an ion down its concentration gradient, leading to no net movement of that particular ion. The Nernst equation takes into account the concentration gradient ([latex]\frac{[ion]_{\text{outside}}}{[ion]_{\text{inside}}}[/latex]), electrical charge of ions ([latex]z[/latex]), as well as temperature ([latex]T[/latex]).
[latex]E_{ion} = \frac{RT}{zF} \ln\left(\frac{[ion]_{outside}}{[ion]_{inside}}\right)[/latex]
Which, when assuming standard body temperature of 37 degrees Celsius and converting ln to log, can be simplified to:
[latex]E_{ion} = \left(\frac{61.54 \, \text{mV}}{z}\right) \log_{10} \left(\frac{[ion]_{outside}}{[ion]_{inside}}\right)[/latex]
Symbol Meanings
[latex]E_{ion}[/latex]: Equilibrium potential (in volts); the membrane voltage necessary for the electrical flux and diffusional flux to oppose each other with equal force.
[latex]R[/latex]: universal gas constant: [latex]8.314 \, \frac{\text{J}}{\text{K$\cdot$mol}}[/latex]; this constant introduces energy into the equation by relating Joules with ion amount (moles) and temperature and is part of the diffusion coefficient used in Fick's first law.
[latex]T[/latex]: temperature in Kelvin; temperature affects kinetic movement of ions across membranes.
[latex]z[/latex]: valence of ion (number of charges). E.g., z = +2 for Ca2+; larger valences will cause the value of [latex]\frac{RT}{zF}[/latex] to drop, making the effect of [latex]\ln\left(\frac{[ion]_{\text{outside}}}{[ion]_{\text{inside}}}\right)[/latex] on Eion smaller, resulting in a smaller absolute value of Eion. This can be understood better by imagining the equilibrium potential of Na+, which is roughly 60 mV: the electrical potential the cell membrane increases to as sodium floods in before finding equilibrium (concentrations of Na are higher outside the cell at rest, creating a concentration gradient driving movement of the ion inward). If the valence of Na+ were to magically double to +2 with all else kept constant, the equilibrium potential would halve to roughly 30 mV. This is because the electrical potential difference across the membrane would only have to be half as strong for the influx of the ion to become balanced with the repulsive electrical forces driving it back out of the cell. On the other hand, if the charge of sodium were to be -1 instead, the concentration would still drive an influx of ions, only that the repulsion of ions back out of the cell would occur when the negative charges started repelling one another, instead of positive charge. The Eion in this case would be roughly -60 mV.
[latex]F[/latex]: Faraday's constant: [latex]96{,}485 \, \frac{\text{c}}{\text{mol}}[/latex]; This serves as a conversion factor between moles and the electrical charge they carry (represented with coulombs). One mole of a single charged ion, such as Na+ or Cl-, carries a charge equal to one Faraday, or 96,485 coulombs. Divalent ions, such as Ca2+, will have 2 Faradays, or 192,970 coulombs, for each mole. When solving for Eion, the units found in the numerator of [latex]\frac{RT}{zF}[/latex] will figure out to [latex]\frac{\text{j}}{\text{mol}}[/latex], and the denominator to [latex]\frac{\text{c}}{\text{mol}}[/latex], leaving us with volts after cancelling out the moles and dividing joules by coulombs ([latex]\text{volts} = \frac{\text{joules}}{\text{coulombs}}[/latex]).
[latex]ln[/latex]: natural logarithm; commonly used when solving equations related to concentrations in biological systems.
[latex][ion]_{\text{outside/inside}}[/latex]: concentration of ion inside/outside of cell in molarity, represented by M (moles of ion per liter of extracellular fluid). Dividing the concentration outside by the concentration inside will give us the concentration gradient.
When a cell membrane is more permeable to an ion, concentrations of that ion inside and outside of the cell are given the opportunity to pursue equilibrium—where there is no net movement of the ion into or out of the cell. This process occurs because of the enduring tendencies of matter outlined in the Minimum Potential Energy Principle and the Second Law of Thermodynamics, which state that systems tend toward equilibrium when given the opportunity. As a result, the cell potential begins to move toward the voltage of the equilibrium potential for that ion.
The Minimum Potential Energy Principle states that a system tends toward a configuration where the amount of potential energy present is low. Areas of high ion concentration have a lot of potential energy relative to those of of low concentration, meaning that the system of the cellular environment will seek to minimize the amount of potential energy through the diffusional flux of ions into the low concentration areas. The Second Law of Thermodynamics goes hand in hand with the minimum potential energy principle, stating that systems tend toward uniformity and equilibrium, where the dispersal of energy is disordered.
| Ion | [ion]outside (in mM) | [ion]inside (in mM) | Eion at 37° Celsius |
|---|---|---|---|
| K+ | 5 | 100 | -80 mV |
| Na+ | 150 | 15 | 62 mV |
| Ca2+ | 2 | 0.0002 | 123 mV |
| Cl- | 150 | 13 | -65 mV |
Typical ion concentrations inside and outside of the neuronal membrane and estimated equilibrium potentials at a typical body temperature of 37° Celsius.
The resting membrane potential for the average neuron is roughly -65 mV, though this varies between different types of neurons. This is primarily due to sodium-potassium pumps, which maintain high intracellular K+ concentration and low intracellular Na+ concentration, and open potassium channels, which allow the cell to be much more permeable to K than other ions at rest. The resulting cell potential during rest (Vm) is going to somewhat resemble the equilibrium potential of K+, which is -80 mV with normal levels of intra- and extracellular concentrations of potassium. Were potassium to be the only ion in the fluid within and outside of the cell, the Vm would be almost exactly -80mV. But because there are other ions present, and because some Na+ permeates into the cell, the resting potential is slightly above potassium’s equilibrium potential.
As potassium leaks out of the neuron due to electrochemical forces, the membrane potential becomes more negative, resembling the equilibrium potential of potassium. ‘Potassium Flow at Rest’ by Casey Henley is licensed under a Creative Commons Attribution Non-Commercial Share-Alike (CC BY-NC-SA) 4.0 International License. View static image of animation.
Maintaining this negative resting state by keeping potassium leak channels open is key to prevent the potential from erroneously reaching the threshold for an action potential in the absence of an excitatory postsynaptic potential.
During EPSPs, the membrane is temporarily altered to become more permeable to Na+ when voltage-gated sodium channels open. This increased permeability is reflected in the rising membrane potential, which starts to move toward the far more positive equilibrium potential of sodium. During IPSPs, a temporary influx of Cl- drives the cell potential downward and away from the potential needed to reach an action potential threshold[1]. The cell potential during inhibitory postsynaptic potentials starts to resemble—you guessed it—the equilibrium potential for chlorine.
Except during excitatory postsynaptic potentials, calcium ions are actively removed from neurons by calcium pumps, using ATP to keep the cell resting potential far away from the equilibrium potential of calcium, which is very positive. Abnormal calcium metabolism or failure to maintain the 10,000 to one ratio of extracellular calcium to intracellular calcium leads to profound neurological deficits as a result of cell depolarization, the downstream effects of which include neurological conditions such as confusion, dizziness, and even as serious as epilepsy[2].
Despite its conceptual utility in understanding the role of equilibrium potentials as it relates to fluctuations in ion permeability and the resulting changes in neuronal membrane potential, the functionality of the Nernst potential equation in practical application is limited as it only takes a single ion into consideration at a time. Using the Nernst equation as a foundation, the Goldman-Hodgkin-Katz voltage equation, simply known as the Goldman equation, takes into account the effect of multiple ions on cell membrane potential, allowing scientists to determine a neuron’s actual voltage potential using information about ion permeability, concentrations, and temperature.
Media Attributions
- Potassium only diffusion only resting membrane © Jim Hutchins and Alexa Crookston is licensed under a CC BY-NC-ND (Attribution NonCommercial NoDerivatives) license
- Sodium only diffusion only resting membrane © Jim Hutchins and Alexa Crookston is licensed under a CC BY-NC-ND (Attribution NonCommercial NoDerivatives) license

