Forces Acting on Ions | The Equilibrium Potential
Objective 3
Compare and contrast the two forces operating on an ion: the diffusion force and the electrical force. State what happens when these two forces are in balance.
The forces operating on charged ions is a complicated topic. You can’t expect to understand it without a bit of effort. But if you put forth that effort, you’ll be rewarded with a deep understanding of the workings of the nervous system.
On the other hand, if you ignore this objective or blow it off, you won’t understand the rest of the Unit. It’s impossible to understand the cellular and molecular biology of the nervous system without getting a good grip on this subject. And it’s not just this Unit: for example, when we cover the electrophysiology of the heart in Unit 16, you’ll need this information.
Let’s break our model down into digestible pieces, then put it back together into a complete understanding.
For this section, we’ll just focus on sodium ions (Na+) and potassium ions (K+). Both are cations, positively charged ions. Both are in Group 1 of the periodic table (Unit 2). Both have one excess proton and therefore one excess packet of positive charge, indicated by the superscript: sodium ions have 11 protons (p+) in the nucleus and 10 electrons (e–) in the electron cloud while potassium ions have 19 packets of positive charge in the nucleus and 18 packets of negative charge in the electron cloud.
Diffusional Forces on Ions
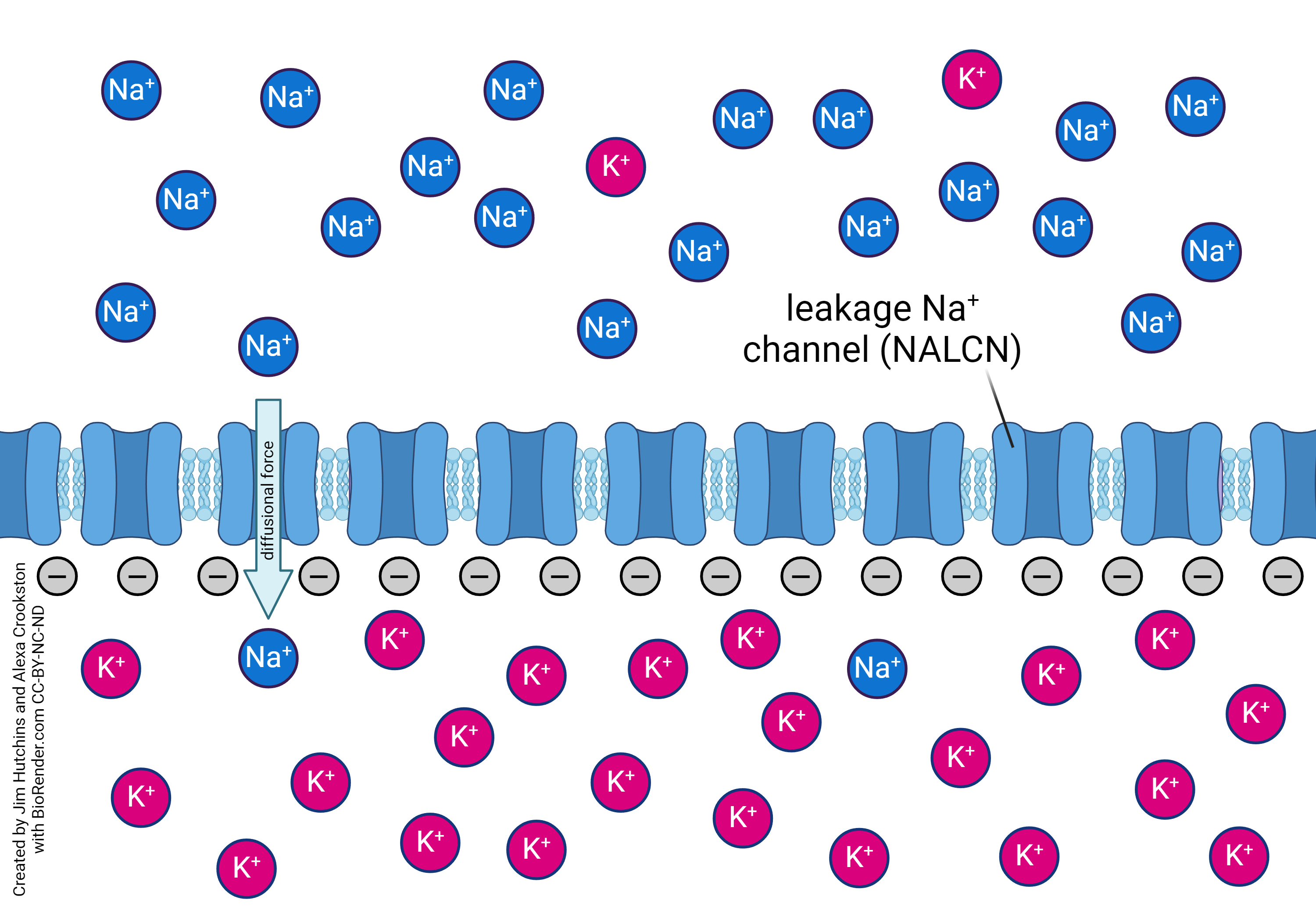
There is more sodium outside the neuron than inside. Therefore, if we just consider the diffusional force (which might also be called the concentration force or the chemical force), and we open a route for sodium to enter or leave, more sodium will enter the neuron than leave because any chemical substance moves from where it is at high concentration to where it is at low concentration, if it has a chance to move. You might remember from Unit 2 that this is a special case of the Second Law of Thermodynamics.
(As an aside, it’s important to note that ions are moving in both directions in all these descriptions, but we generally simplify the discussion by considering the net flux, that is, which direction of movement predominates. In real terms, a single electrical event in neurons represents an excess of 10,000 sodium or potassium ions moving in one direction or the other but that’s definitely not a number you need to know. Thus the net flux would represent 1,000,000 sodium ions moving inside and 990,000 sodium ions moving out.)
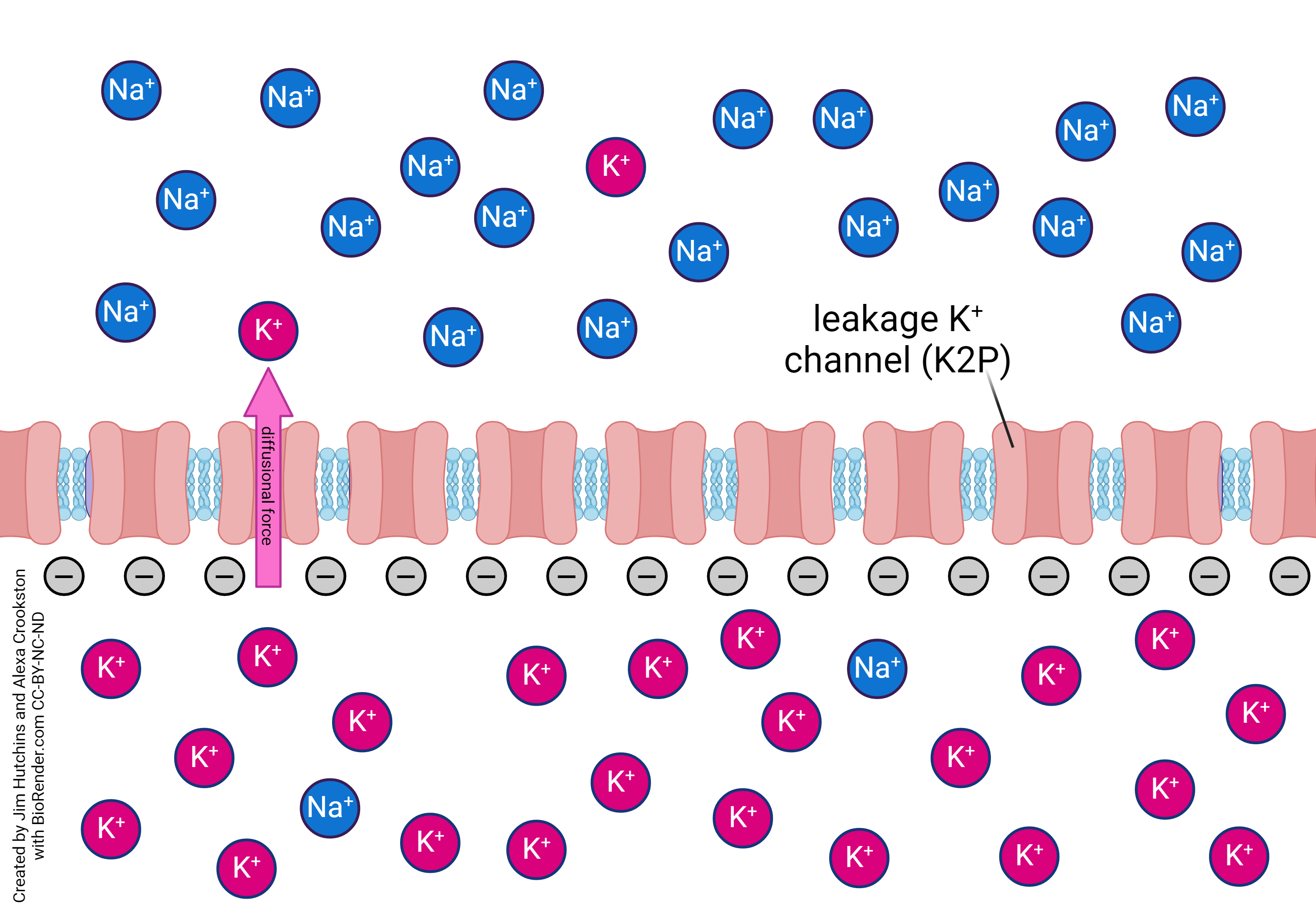
There is more potassium inside the neuron than outside. Therefore, if we just consider the diffusional force, and we open a route for potassium to enter or leave, more potassium will leave the neuron than enter because any chemical substance moves from where it is at high concentration to where it is at low concentration, if it has a chance to move.
To summarize, for the diffusional force considered in isolation,
Diffusional Force
sodium moves into the neuron
potassium moves out of the neuron
Electrical Forces on Ions
At the same time as there is a diffusional force, there is an electrical force, because the particles that are diffusing are ions: that is, they have an electrical charge.
Let’s consider the electrical force in isolation. This one is much easier, because either the inside of the neuron has an excess of negative charges, or it has an excess of positive charges. In both cases, the ions we’re considering (Na+ and K+) are cations, or positively charged.
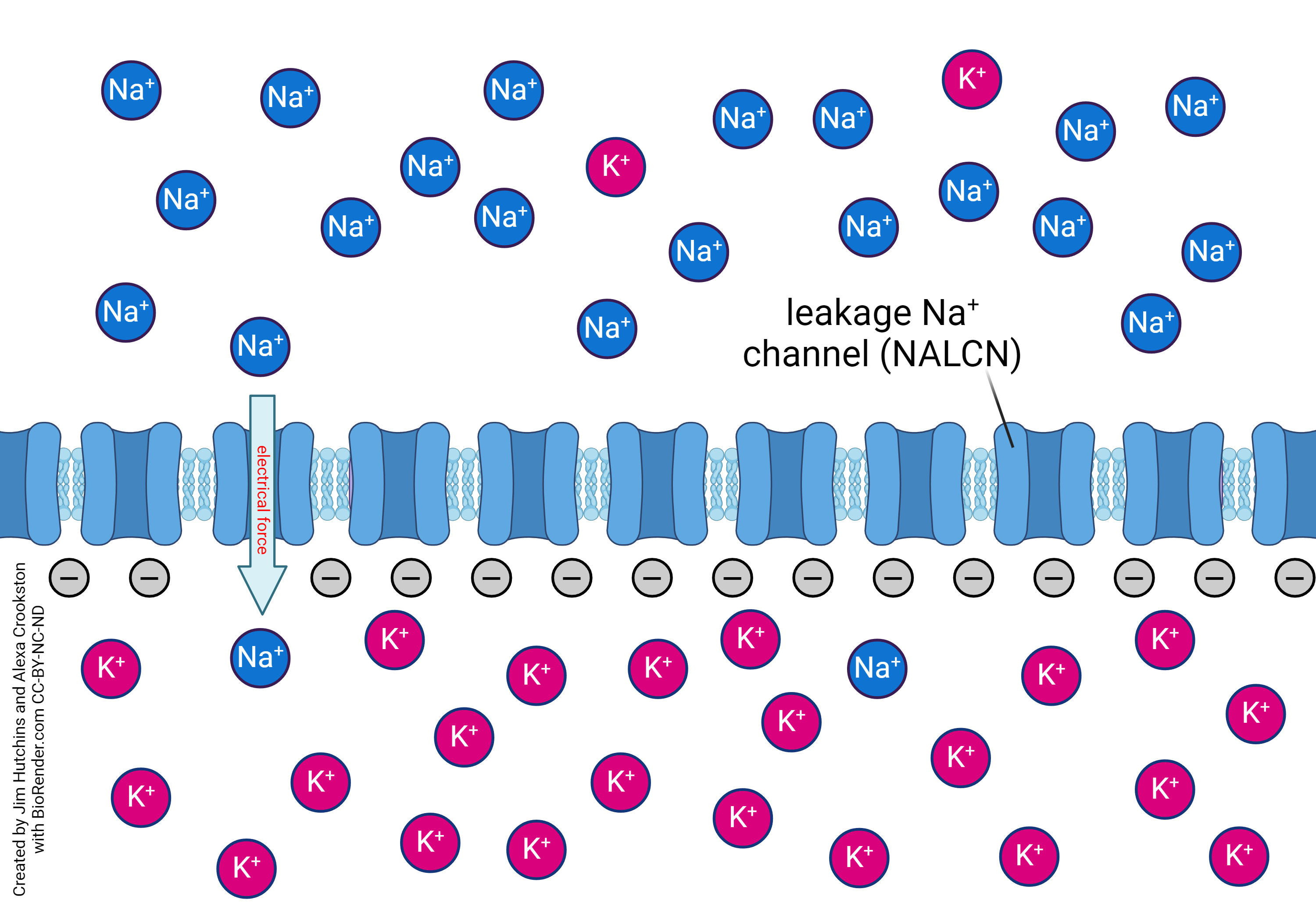
When the inside of the neuron is negatively charged, Na+ ions are attracted to the inside of the cell by the electrical force. The diffusional force is unchanged from the previous diagram, because the diffisional force is only a function of the concentrations of sodium outside and inside, not what’s going on with charges. K+ ions move the same way, so this is not shown in the diagram.
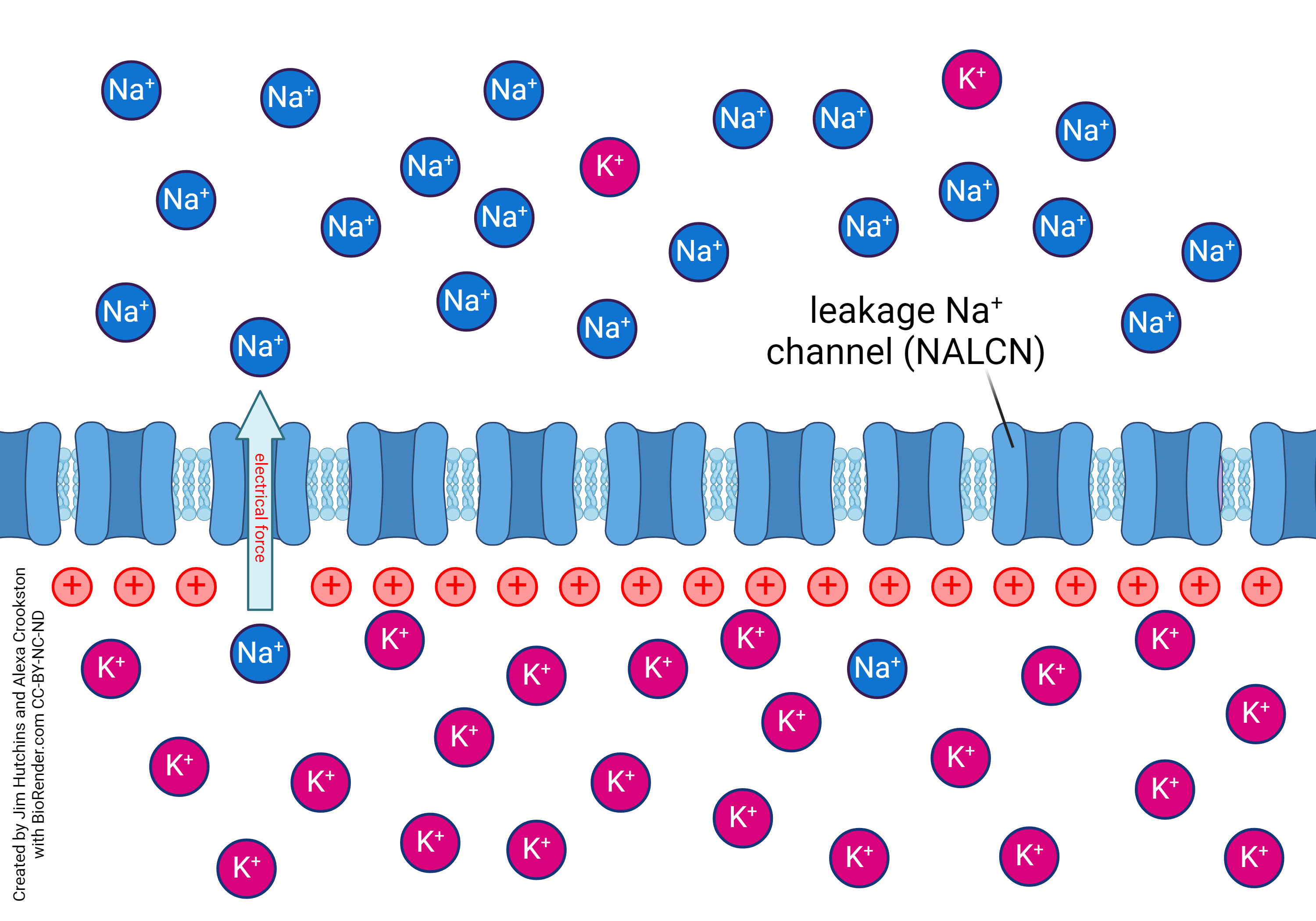
When the inside of the neuron is positively charged, Na+ ions are repelled from the inside of the cell by the electrical force. Note that only the electrical force “arrow” has changed direction. The diffusional force is not affected by electrical charge. K+ ions move the same way, so this is not shown in the diagram. When the inside of the neuron is positively charged, both Na+ and K+ are repelled by the excess positive charges inside the cell and the net flux of both ions is out of the cell.
To summarize, for the electrical force considered in isolation,
Electrical Force
sodium & potassium move into the neuron when it is negatively charged
sodium & potassium move out of the neuron when it is positively charged
We’ve thought about diffusion forces and electrical forces separately. Now let’s combine them, taking one ion at a time.
These two panels depict the forces on potassium ions under two different conditions. The inside of the neuron is at the bottom, so the only change in conditions is the excess negative charges inside the neuron in the left panel and the excess positive charges inside the neuron in the right panel.
When the inside of the neuron is negatively charged, the diffusion force and electrical force are in opposition. The diffusion force wants to push potassium out. The electrical force wants to pull potassium in.
Who “wins” depends on the voltage (or potential), which represents the size of the electrical force.
The Equilibrium Potential
Now do a thought experiment. Imagine that we can set the voltage (potential) so that these two forces exactly balance each other out. We will call this the equilibrium potential (E).
The word “equilibrium” is Latin: æqui, “equal” + libra, “balance” (from which we get the astrological sign Libra, or the abbreviation “lb.” for “pounds”). The equilibrium potential, then, is literally when we get an equal balance of forces at a specific voltage.
Let’s re-examine the sodium image we saw above, but now consider the balance of forces.
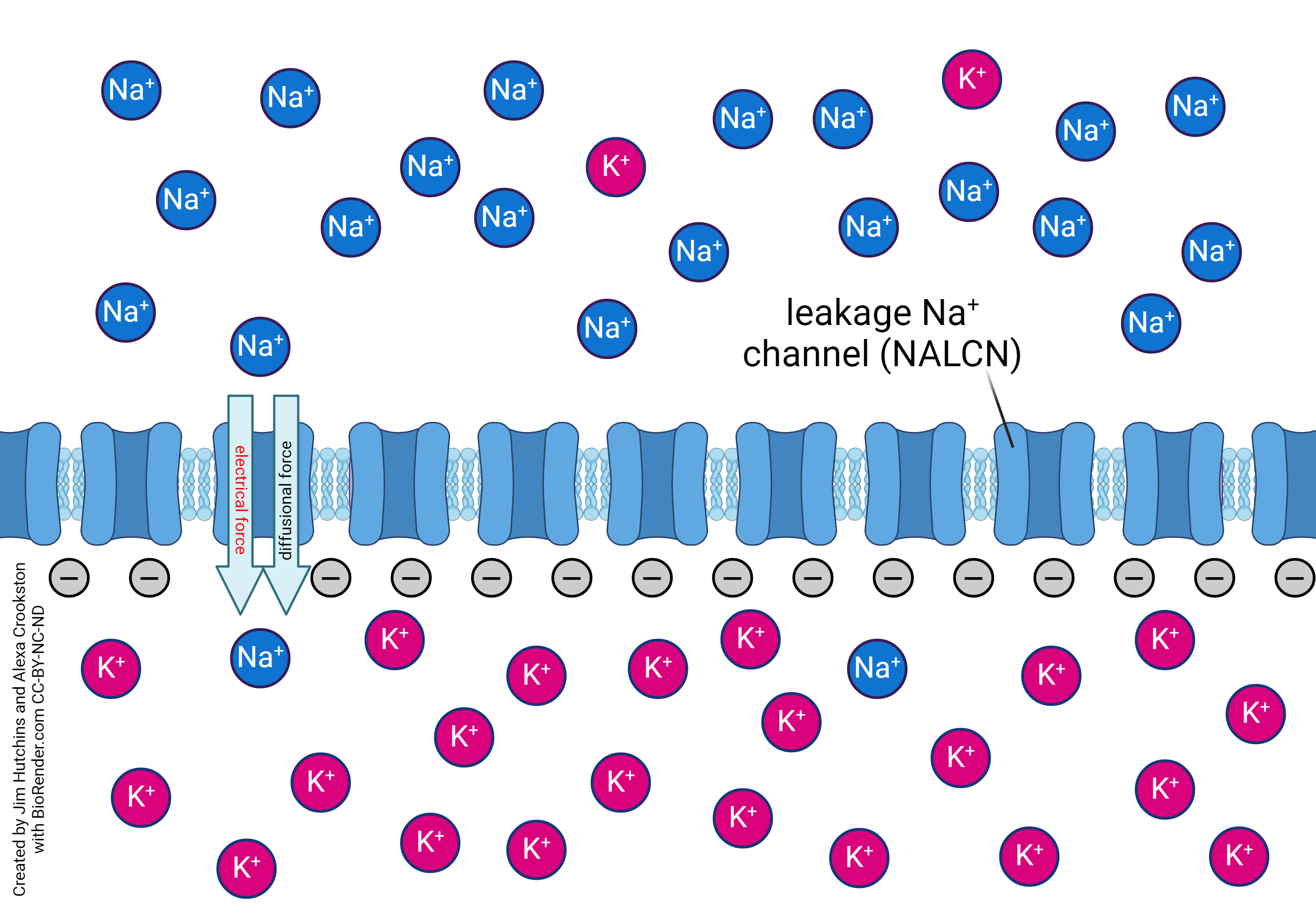
If the voltage inside the neuron is negative, then these forces can never be in balance. (Both arrows point in the same direction.) Sodium will want to enter the neuron based on the diffusion force. Sodium will want to enter the neuron even more based on the electrical force. No matter what, sodium is going to enter.
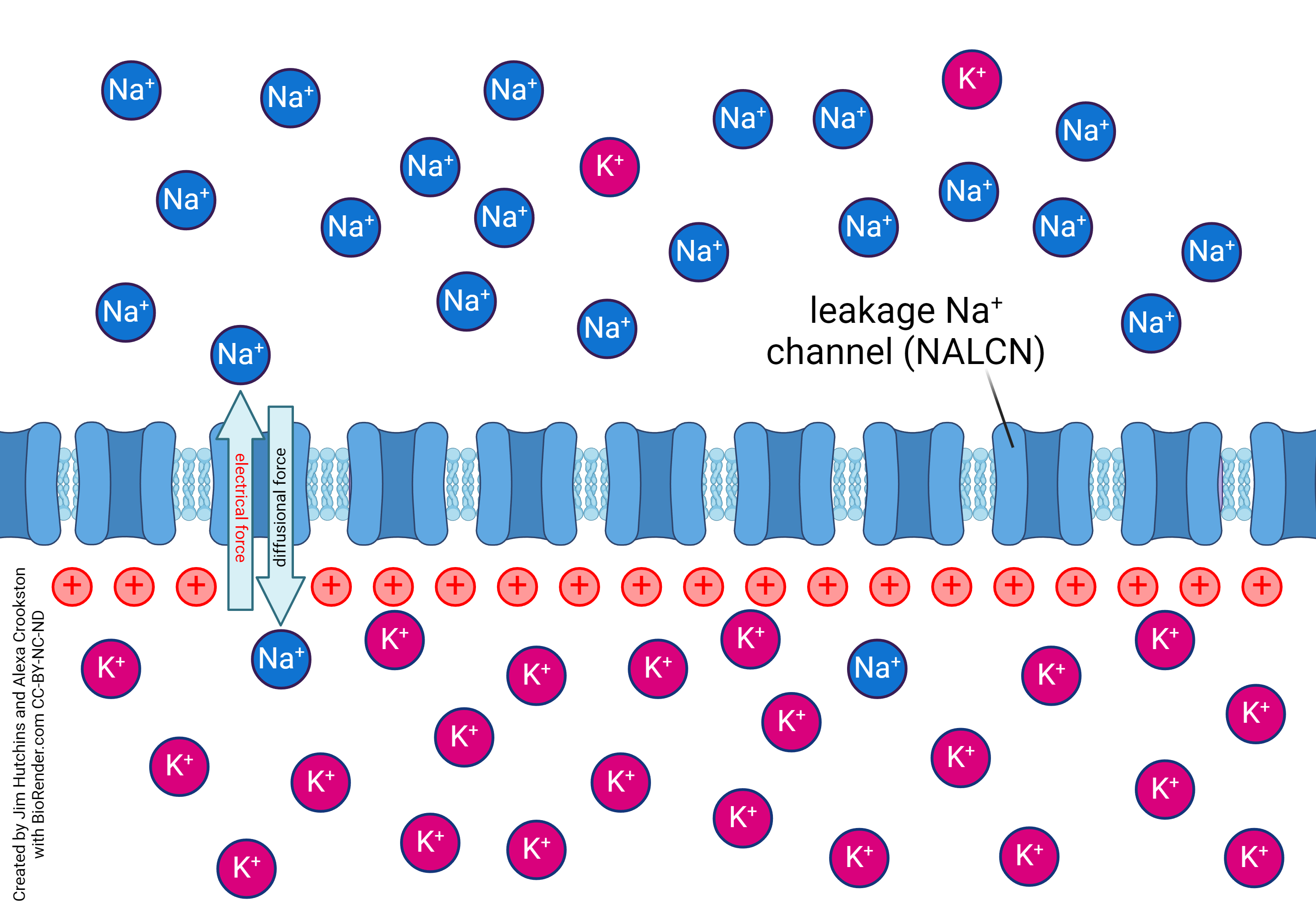
If the voltage inside the neuron is positive, then these forces can achieve a balance or equilibrium. (Arrows point in opposite directions.) The equilibrium potential for sodium (ENa) is typically about +60 mV. But don’t learn this number because very few neurons are typical. We just need a rough number to work with as we develop these ideas further.
Now let’s do the same thought experiment but with potassium ions.
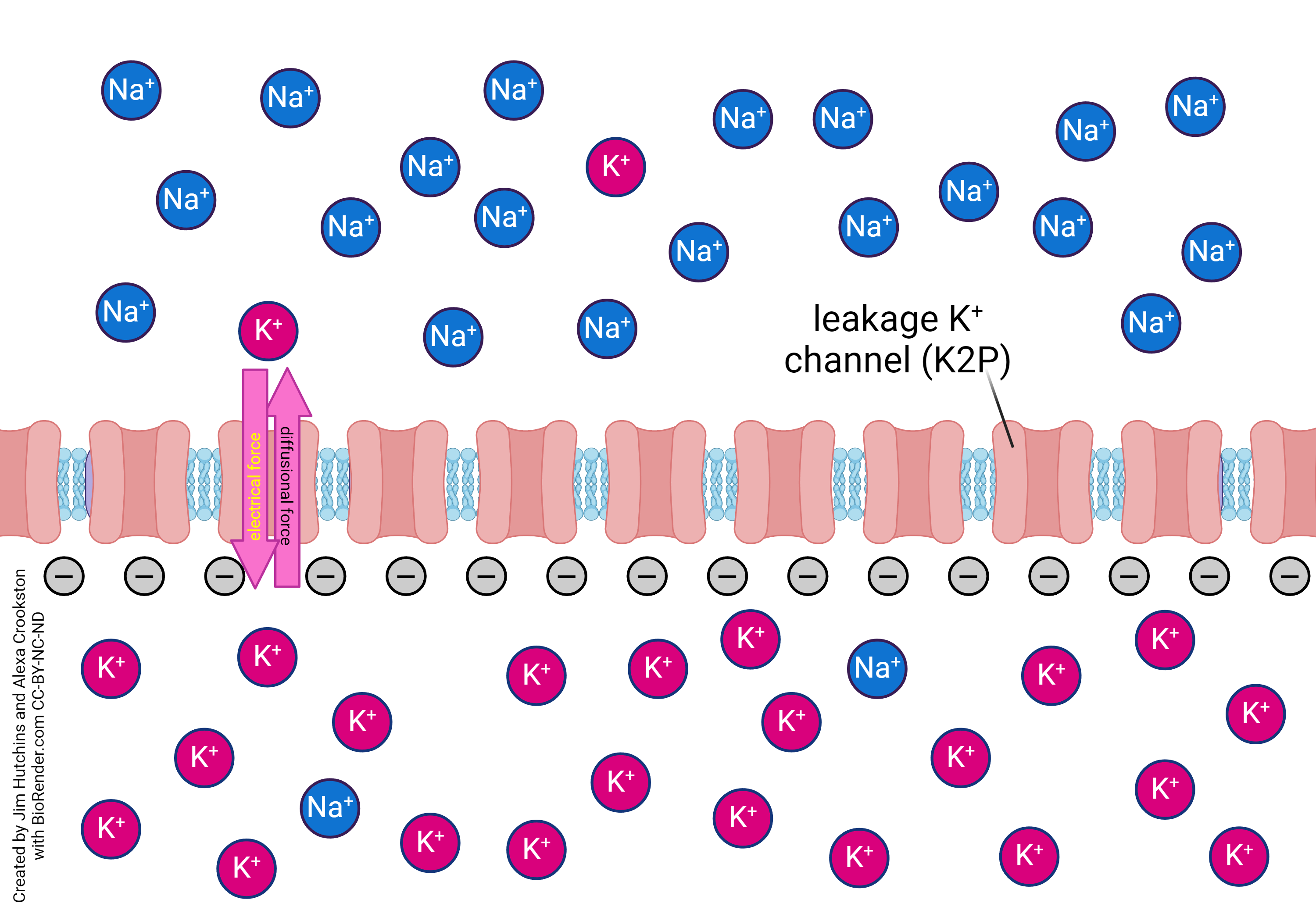
If the voltage inside the neuron is negative, then these forces can be in balance. Potassium will want to leave the neuron based on the diffusion force. Potassium will want to enter the neuron based on the electrical force. At some value of the membrane voltage, these forces are going to be balanced. The equilibrium potential for potassium (EK) is typically about –80 mV.
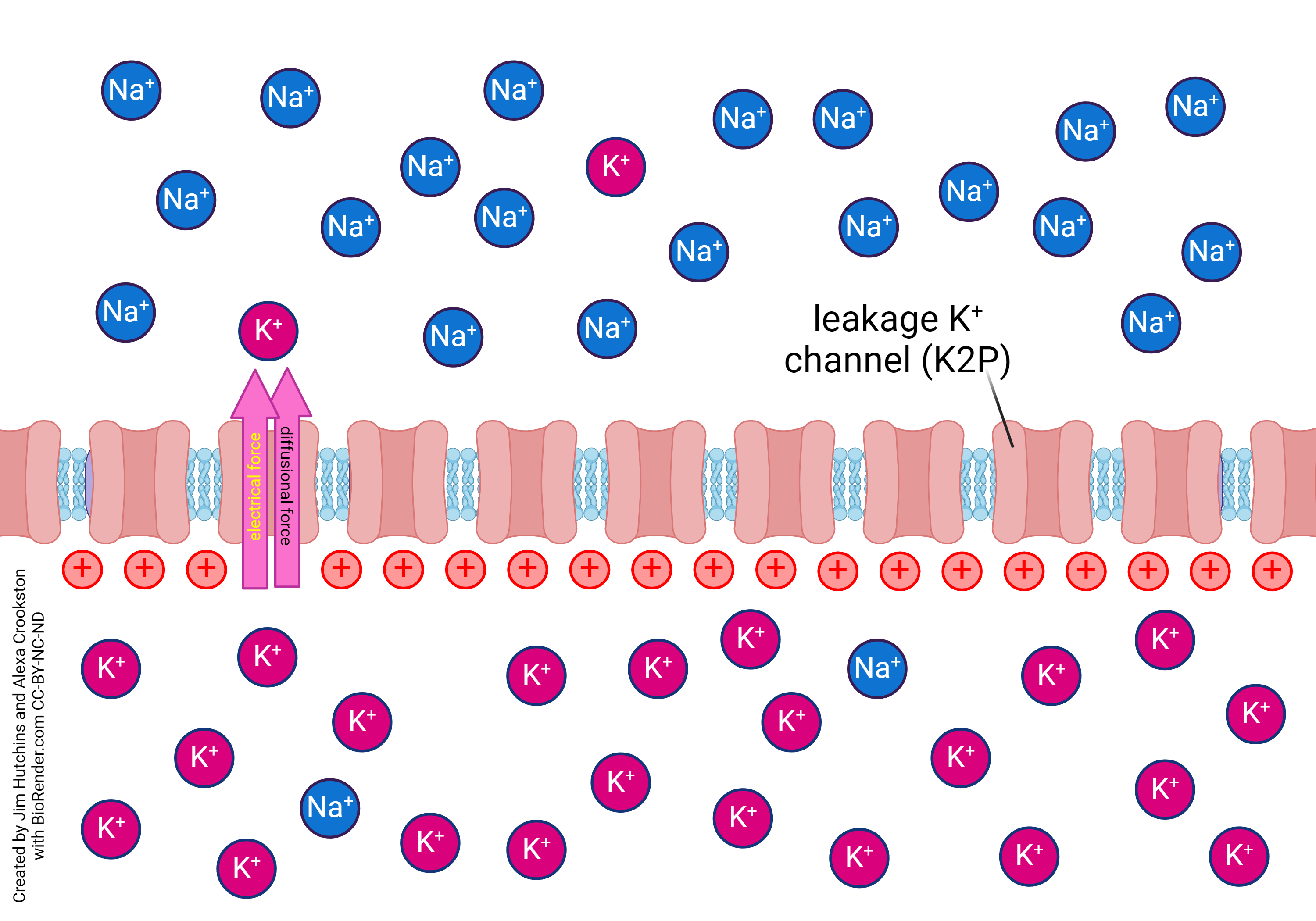
If the voltage inside the neuron is positive, then these forces can never be in balance. Potassium will want to leave the neuron based on the diffusion force. Potassium will want to leave the neuron based on the electrical force. No matter what, potassium is going to leave.
The Resting Potential
Because (almost) all cells have the same distribution of sodium and potassium ions, and (almost) all cells have leakage channels for sodium and potassium, all cells have a resting potential that is negative inside.
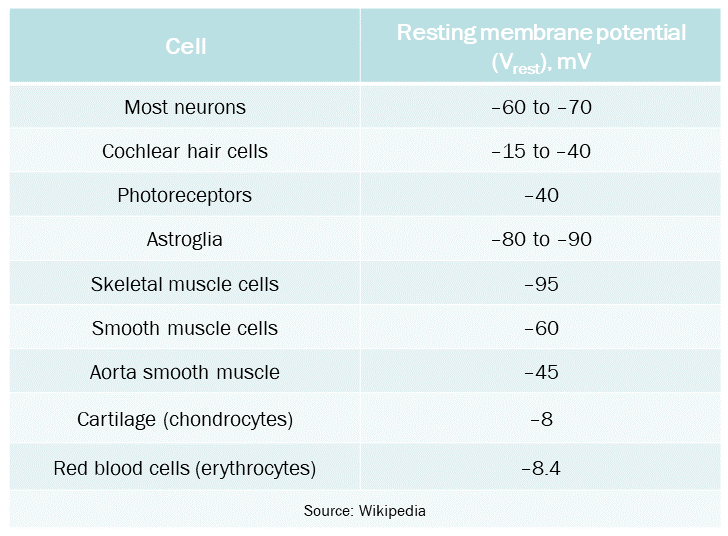
This table shows values for the resting potential for a variety of different cells. Almost all cells are slightly more negative inside than outside.
For a neuron, the resting potential (i.e. resting voltage) is the voltage that a neuron holds when it’s not doing anything especially neuron-ish. As you can see, the numbers vary for different kinds of neurons. Other excitable cells (e.g. muscle cells) also have large negative resting potentials. Non-excitable cells (cartilage, red blood cells) have a small but significant negative voltage inside.
Where does the resting potential come from? It’s a balance of the equilibrium potentials for potassium and sodium. You can think of it as a kind of “average” of the action of all the leakage channels for potassium and leakage channels for sodium.
If we only had leakage channels for potassium in the neuronal membrane, we’d rapidly reach equilibrium for potassium (say, –80 mV). If we only had leakage channels for sodium in the neuronal membrane, we’d rapidly reach equilibrium for sodium (say, +60 mV).
If we had both kinds of leakage channels in equal numbers, the resting potential would be close to the average of –80 mV and +60 mV or about –10 mV. That’s the case in non-excitable cells.
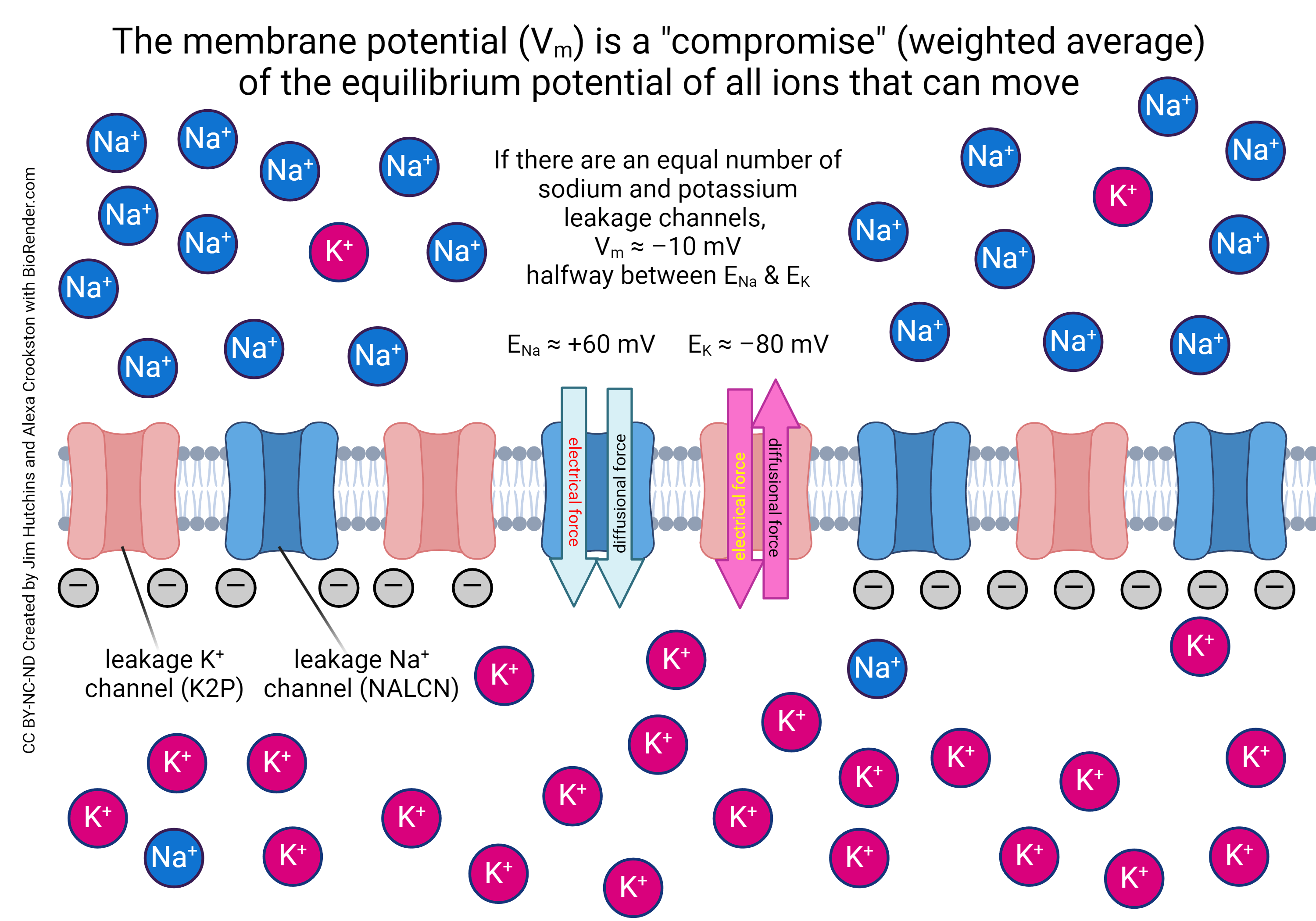
If, on the other hand, we had a lot more potassium leakage channels than sodium leakage channels in the neuronal membrane (NARRATOR: we do) then the resting membrane potential would be a lot closer to the potassium equilibrium potential.
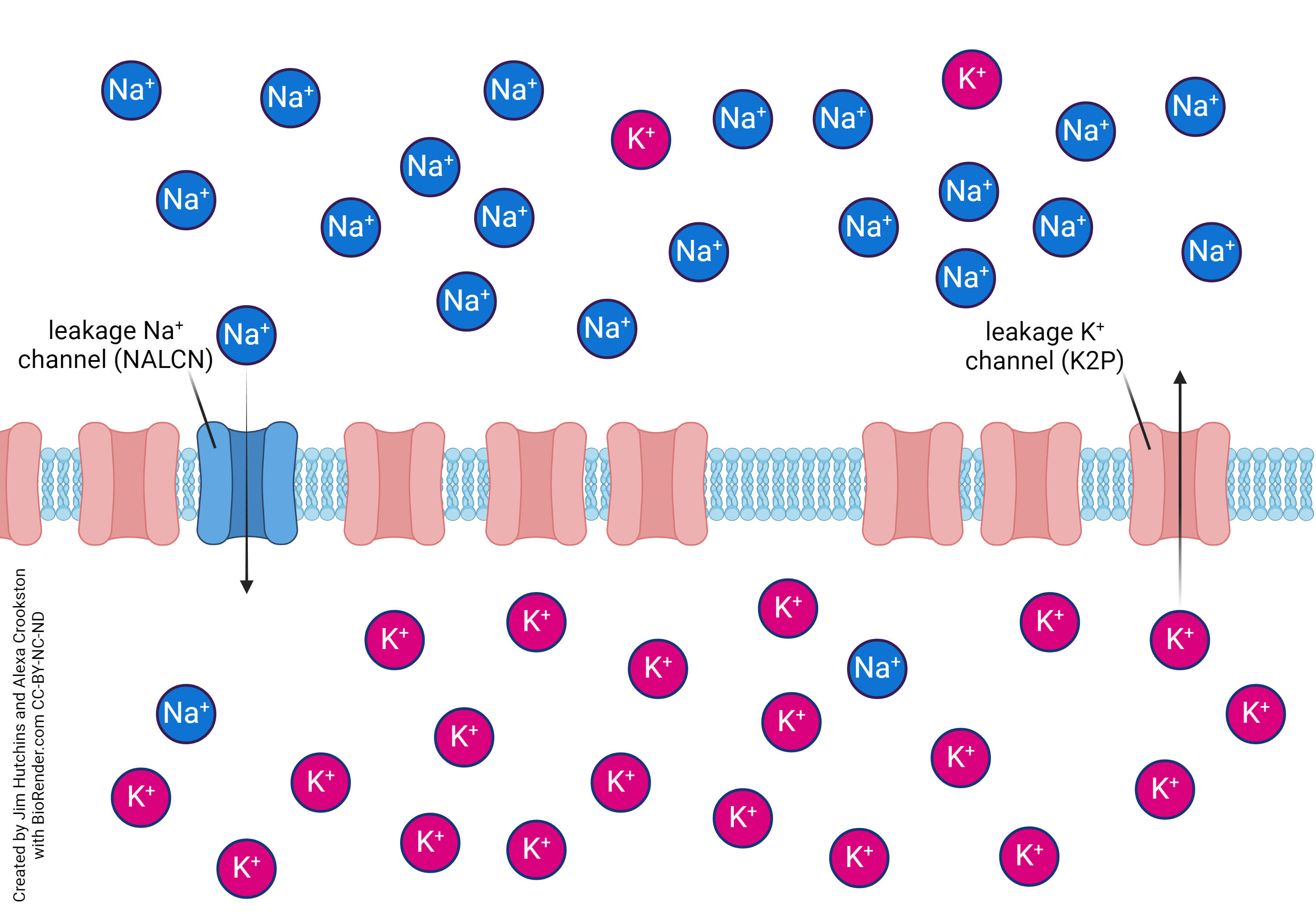
For a typical neuron, there are about 14 leakage potassium channels in the neuronal membrane for every 1 leakage sodium channel. As we would expect, then, the resting potential is much much more greatly influenced by the potassium equilibrium potential than the sodium equilibrium potential because the potassium “team” is 14 times stronger than the sodium “team”. Put another way, the equilibrium potential must lie between the sodium equilibrium potential (+60 mV) and the potassium equilibrium potential (–80 mV) but it’s very close to EK because of the preponderance of leakage potassium channels.
In formal terms, we say the permeability (ability to move) of the membrane to potassium ions is about 14 times the permeability of the membrane to sodium ions.
Media Attributions
- U13-019 Sodium only Diffusion only Resting Membrane © Hutchins, Jim and Crookston, Alexa is licensed under a CC BY-NC-ND (Attribution NonCommercial NoDerivatives) license
- U13-020 Potassium only Diffusion only Resting Membrane © Hutchins, Jim and Crookston, Alexa is licensed under a CC BY-NC-ND (Attribution NonCommercial NoDerivatives) license
- U13-020a Sodium only Electrical only Resting Membrane © Hutchins, Jim and Crookston, Alexa is licensed under a CC BY-NC-ND (Attribution NonCommercial NoDerivatives) license
- U13-020b Sodium only Electrical only Positive Inside © Hutchins, Jim and Crookston, Alexa is licensed under a CC BY-NC-ND (Attribution NonCommercial NoDerivatives) license
- U13-021 Sodium only Equilibrium Resting Membrane © Hutchins, Jim and Crookston, Alexa is licensed under a CC BY-NC-ND (Attribution NonCommercial NoDerivatives) license
- U13-022 Sodium only Equilibrium Positive Inside © Hutchins, Jim and Crookston, Alexa is licensed under a CC BY-NC-ND (Attribution NonCommercial NoDerivatives) license
- U13-023 Potassium only Equilibrium Resting Membrane © Hutchins, Jim and Crookston, Alexa is licensed under a CC BY-NC-ND (Attribution NonCommercial NoDerivatives) license
- U13-024 Potassium only Equilibrium Inside Positive © Hutchins, Jim and Crookston, Alexa is licensed under a CC BY-NC-ND (Attribution NonCommercial NoDerivatives) license
- U13-025 Resting Potential Table © Hutchins, Jim is licensed under a CC BY-SA (Attribution ShareAlike) license
- U13-026a Resting Membrane Sodium and Potassium Channels Equal (1) © Hutchins, Jim and Crookston, Alexa is licensed under a CC BY-NC-ND (Attribution NonCommercial NoDerivatives) license
- U13-026 Resting Neuronal Membrane Ion Distribution and Leakage Channels © Hutchins, Jim and Crookston, Alexa is licensed under a CC BY-NC-ND (Attribution NonCommercial NoDerivatives) license

