The Nernst Equation
Cody Zundel and Jim Hutchins
[latex]V_{m} := V_{in}- V_{out}[/latex]
[latex]E_{i}= V_{m}(I = 0)=_{def} V_{in}- V_{out} = \frac{RT}{zF}ln \frac{[C]_{out}}{[C]_{in}}[/latex]
[latex]E_{i} = 58 \, mV \, log_{10} \frac{[C]_{out}}{[C]_{in}}[/latex]
[latex]E_{i} = 62 \: mV \, log_{10} \frac{[C]_{out}}{[C]_{in}}[/latex]
[latex]I = J \cdot zF= -(uz^2 F[C] \frac{\partial V}{\partial x} + uzRT \frac{\partial [C]}{\partial x})[/latex]
[latex]I = -(uz^2 F[C] \frac{\partial V}{\partial x} + uzRT \frac{\partial [C]}{\partial x}) = 0[/latex]
[latex]\frac{\partial V}{\partial x} = \frac{-RT}{zF} \frac{1}{[C]} \frac{\partial [C]}{\partial x}\rightarrow \int_{x_{1}}^{x_{2}} \frac{dV}{dx}dx = \frac{-RT}{zF}\int_{x_{1}}^{x_{2}} \frac{d[C]}{[C]dx}dx[/latex]
[latex]\int_{V_{1}}^{V_{2}}dV = -\frac{RT}{zF}\int_{[C]_{1}}^{[C]_{2}} \frac{d[C]}{[C]dx}[/latex]
[latex]V_{2} - V_{1} = -\frac{RT}{zF}ln \frac{[C]_{2}}{[C]_{1}}[/latex]
[latex]E_{ion} = \frac{RT}{zF}ln \frac{[ion]_{out}}{[ion]_{in}}[/latex]



Media Attributions
- Slide13
- Slide12
- Slide20
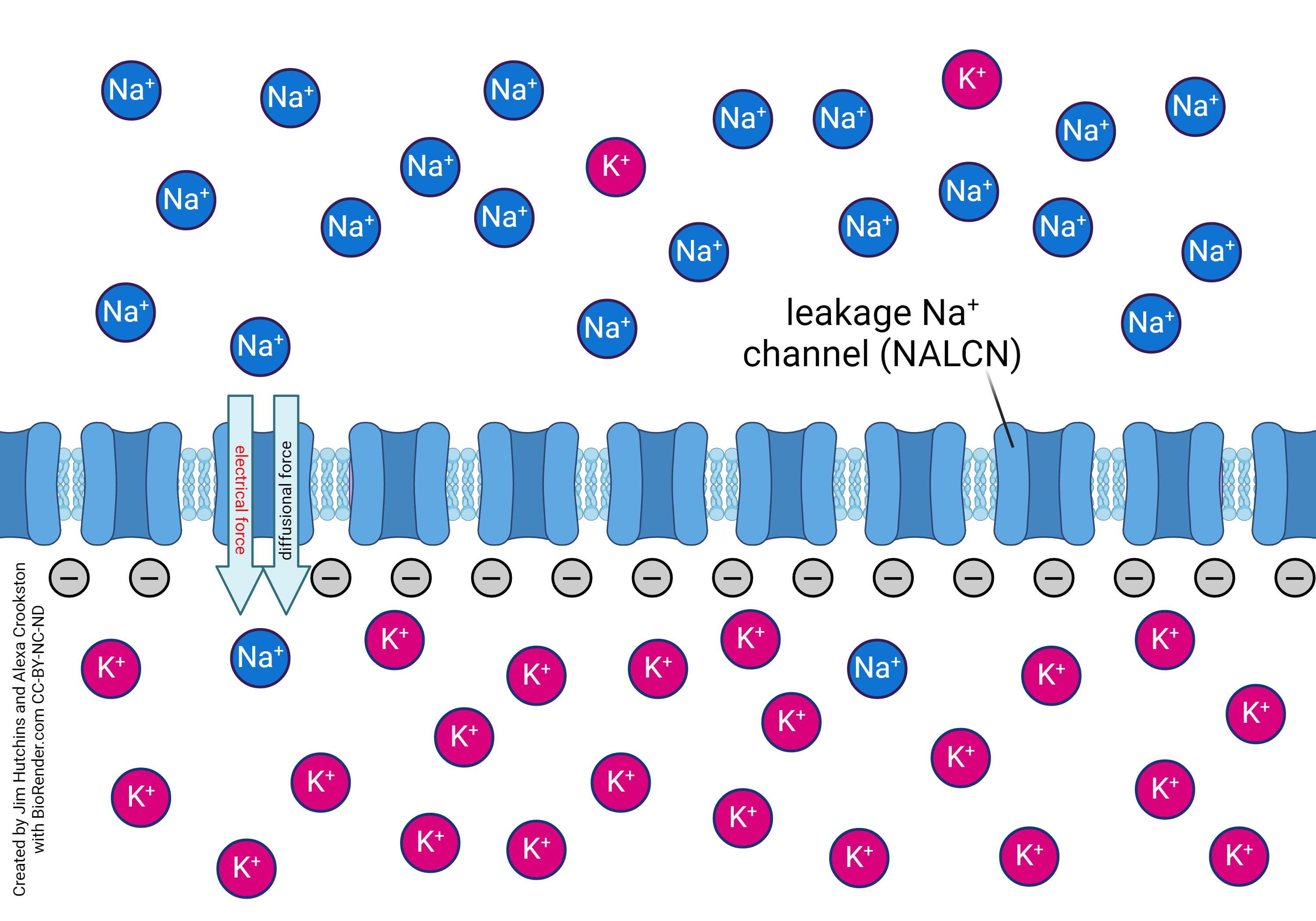
- Sodium only equilibrium resting membrane © Jim Hutchins is licensed under a CC BY-NC-ND (Attribution NonCommercial NoDerivatives) license
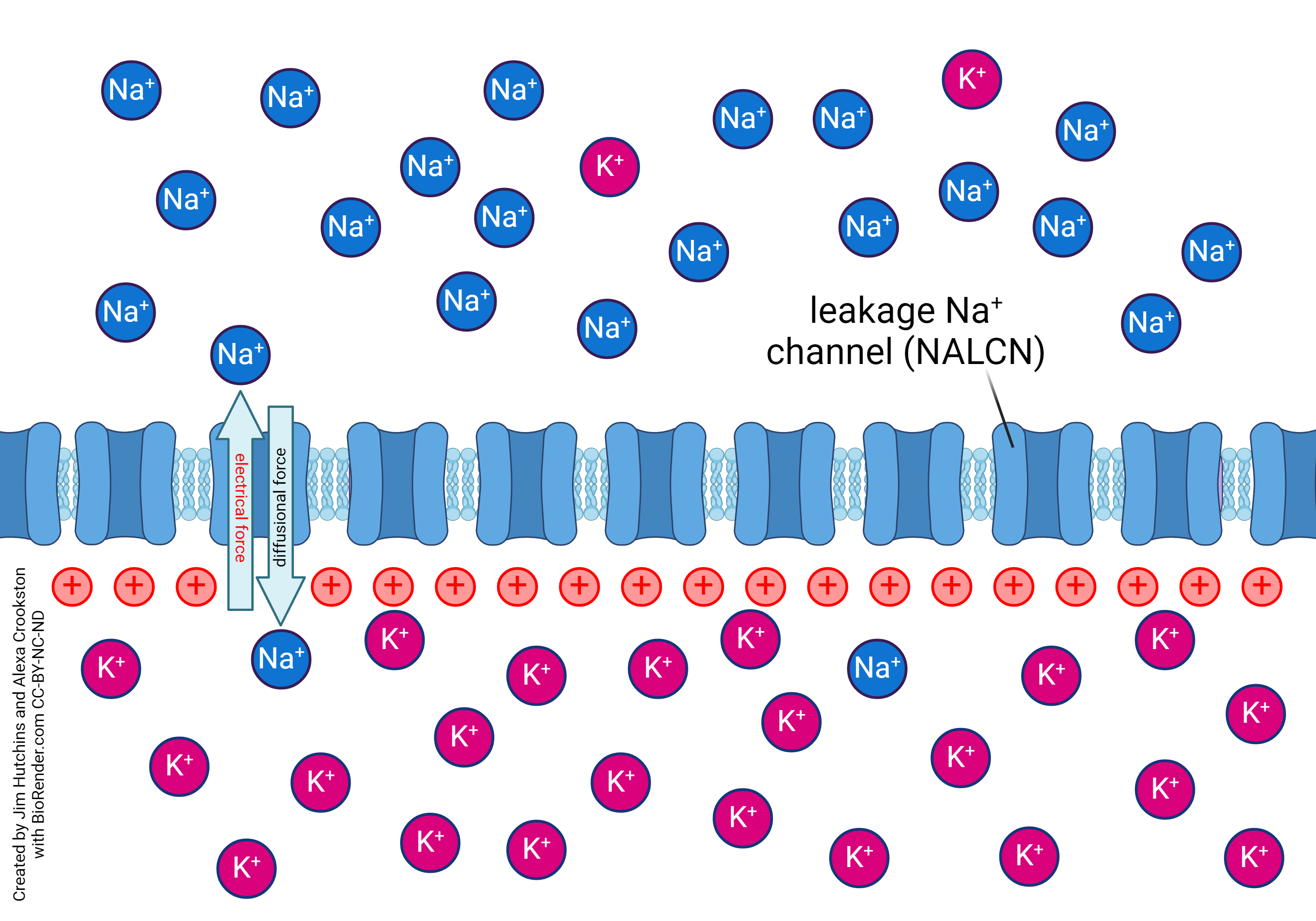
- Sodium only equilibrium positive inside © Jim Hutchins is licensed under a CC BY-NC-ND (Attribution NonCommercial NoDerivatives) license
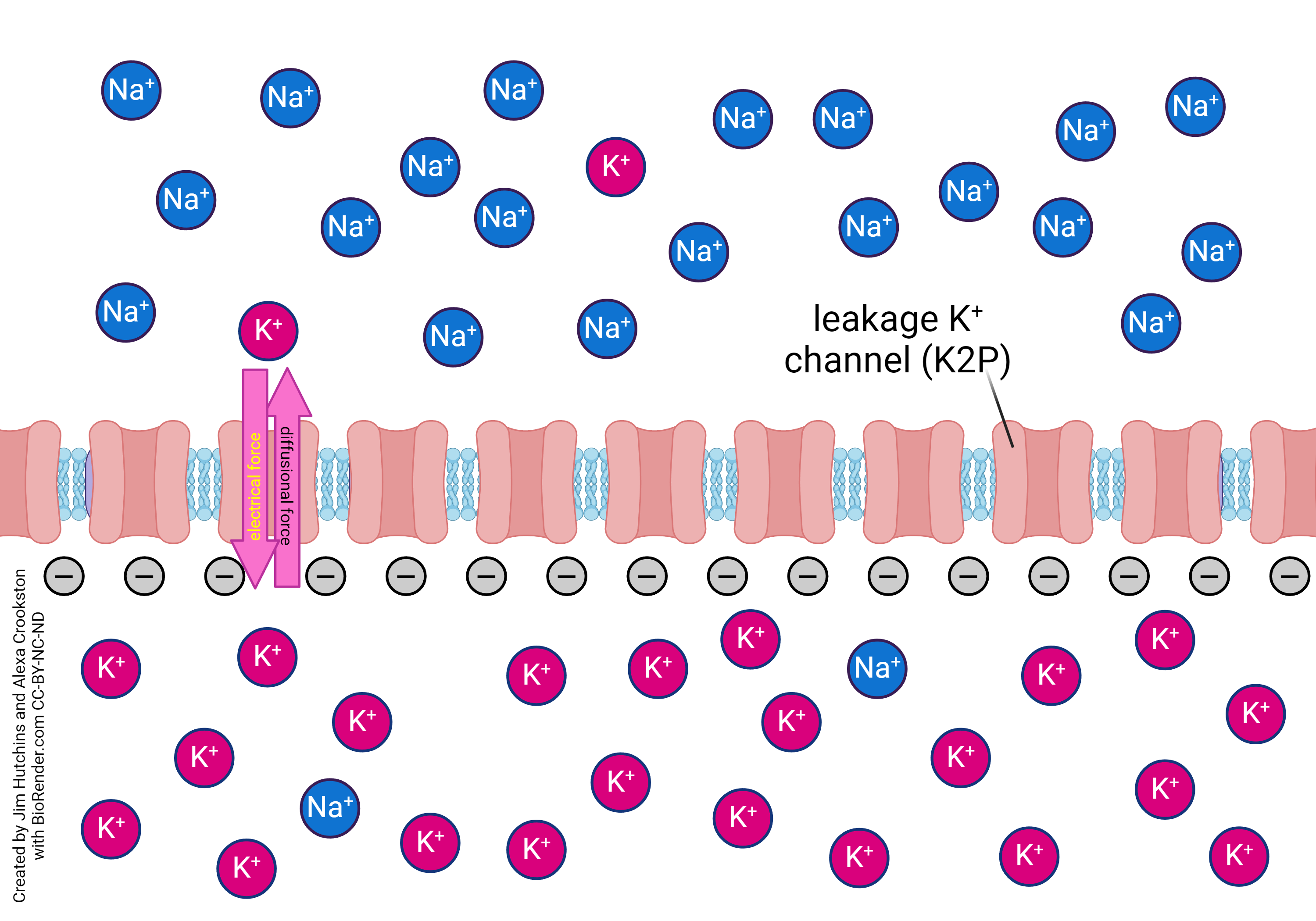
- Potassium only equilibrium resting membrane © Jim Hutchins is licensed under a CC BY-NC-ND (Attribution NonCommercial NoDerivatives) license
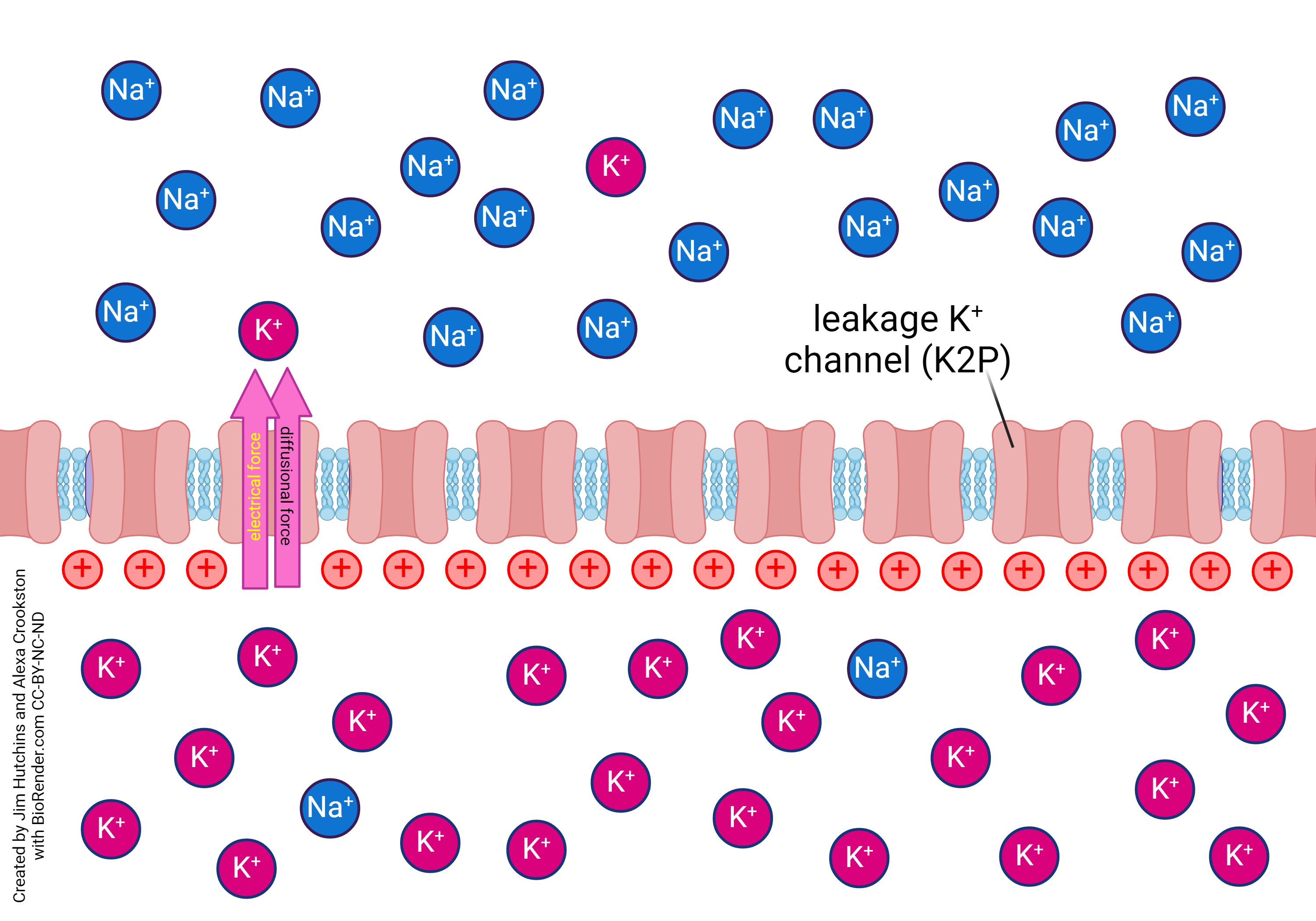
- Potassium only equilibrium inside positive © Jim Hutchins is licensed under a CC BY-NC-ND (Attribution NonCommercial NoDerivatives) license

