Cable Theory and Electrical Current Flow in Neurons
Jim Hutchins and Cody Zundel
This article explains cable theory in mathematical terms. For a non-mathematical treatment and historical background, see the Introduction to Neuroscience article on signal processing in neurons.
We will only touch on the very superficial mathematics related to cable theory in neurons, but the interested student who is not afraid of some seriously tough mathematics is directed to the book I used in graduate school: Jack JJB, Noble D, and Tsien RW, Electric Current Flow in Excitable Cells (1975), which is now available for free.
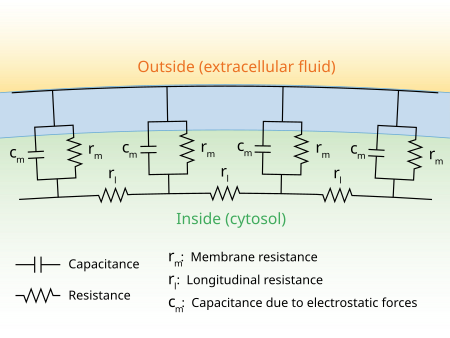 Remember that Hodgkin and Huxley modeled the neuronal membrane as an equivalent circuit, that is, a way of envisioning the neuronal cell membrane and cytoplasm as a set of electrical components wired together.
Remember that Hodgkin and Huxley modeled the neuronal membrane as an equivalent circuit, that is, a way of envisioning the neuronal cell membrane and cytoplasm as a set of electrical components wired together.
For our purposes, we only need to master two concepts. The first is the easier one: as an electric current travels in space, it gets smaller in a steady and mathematically predictable way. Neuroscientists say it decrements in space.
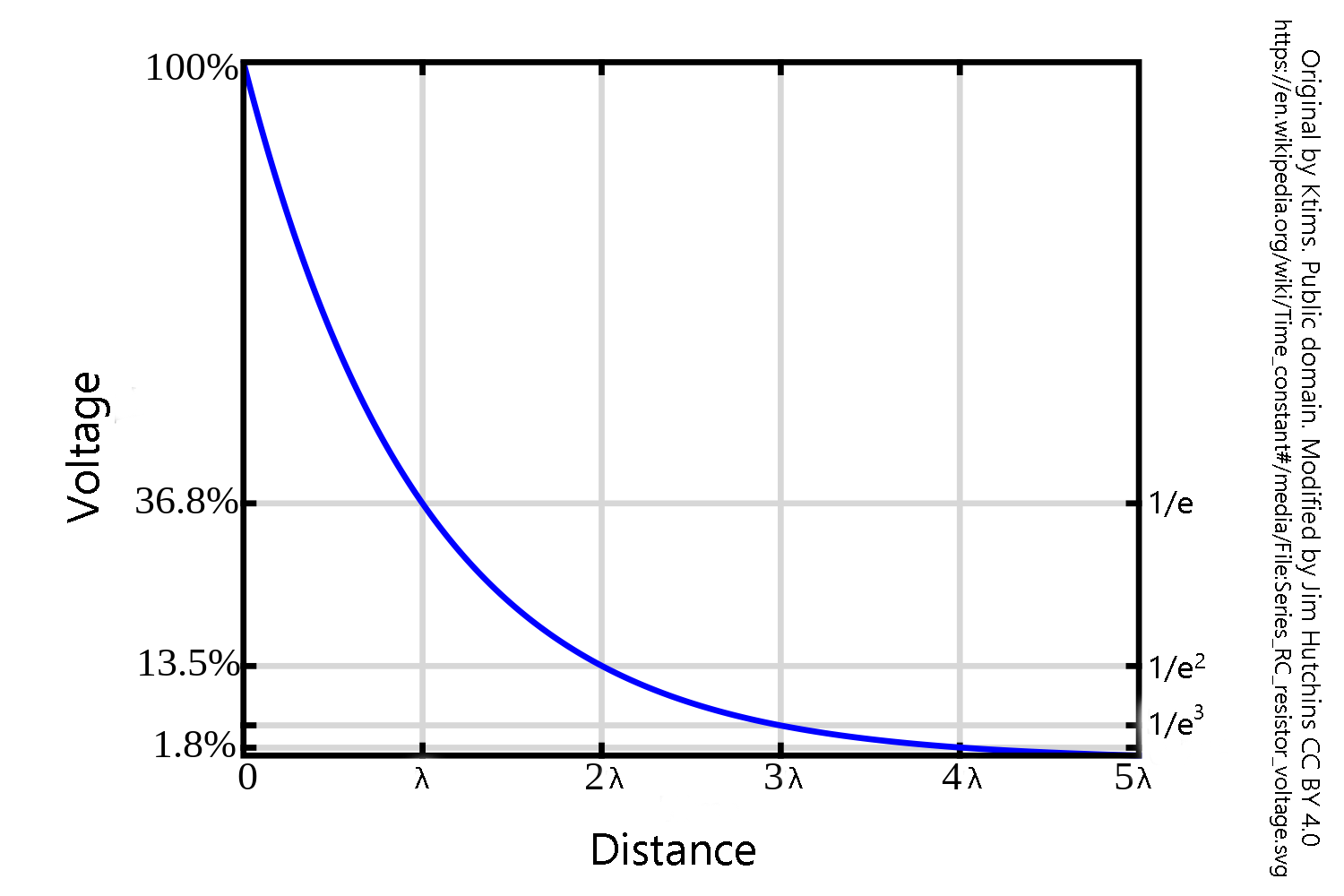
Let’s say lightning strikes a large lake where you are swimming. At a short distance from the place where the lightning strikes, you would be subjected to 300 million volts. Some distance away — for us, the distance doesn’t matter too much but the concept does — it would be at 110 million volts, or 36.8% of the original voltage. Twice that distance, and it would be at 40 million volts (13.5%); three times that distance, 15 million volts (5%); four times that distance, 5.4 million volts (1.8%), and five times that distance, 2 million volts (0.7%). To describe the mathematics, we use a constant you may have not seen before called e (Euler’s constant). It came up when we were discussing the Nernst equation, because it is the base used for the logarithm of the relative concentration (loge), but we tossed it out pretty quickly in favor of the log10 that is easier for most students to understand (but by no means easy, just easier). Like the more familiar π, e is an irrational, transcendental number (its digits go on forever).
To simplify things somewhat, there is a graph above that shows this concept. The distance over which the voltage decrements by 1/e (1/2.71828···) is called the length constant and symbolized by the Greek letter lambda (λ). At two length constants, the voltage is now the original voltage divided by e2; at three length constants, the original voltage divided by e3; and so forth. In our original example, after 20 length constants, the voltage of 300 million volts is divided by e20 or a manageable 0.6 V, less than a AA battery.
For neurons, the length constant varies from about 1 mm in large-caliber axons to about 0.1 mm in smaller axons. For example, an action potential is about 100 mV. In the largest axons in the human body, that voltage will decrement to 1.8 mV (100/e4 mV) just 4 mm away from the axon hillock where we initiated the action potential. This is well below threshold for firing a new action potential. Without some sort of periodic boost like that provided by the node of Ranvier, there would not be much voltage left even a short distance away from the cell body of a neuron. Another strategy would be continuous conduction of an action potential, but as we’ve seen, that has the disadvantage of slowing down action potential conduction because of the time taken to open and close voltage-gated Na+ and K+ channels.
Notably, in dendrites, a very small voltage change at the synapse (typically less that 1 mV) becomes very small indeed over a distance of several millimeters.
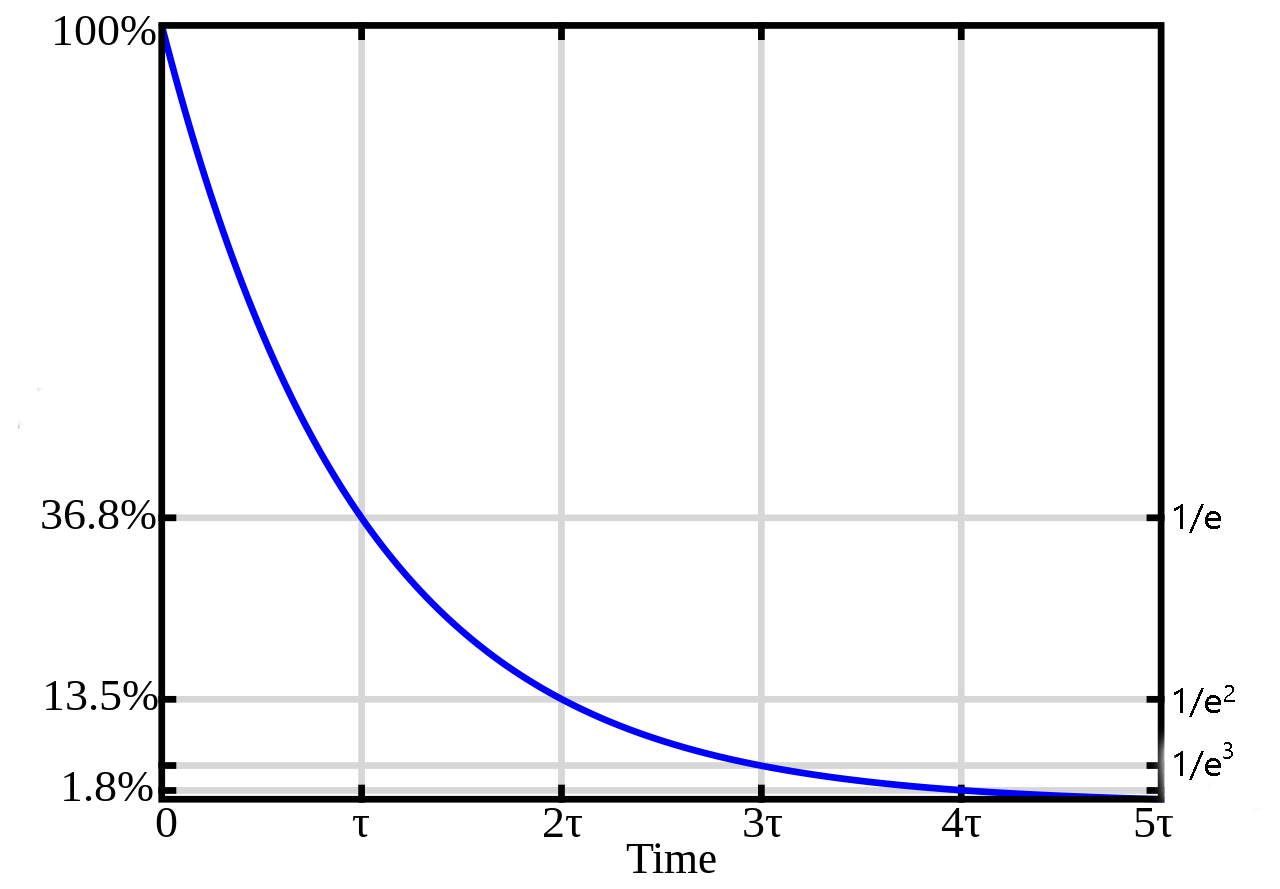
Now apply the same sort of analysis to time. Let’s say you’re wading in your favorite lake and lightning strikes in your exact location. You’re going to experience 300 million volts. But over a few seconds, that voltage change will have decremented and become near-zero fairly quickly. If you’re swimming in the exact spot where lightning struck yesterday, it is extremely unlikely that you will experience any change in voltage. Again, we describe a constant, now called the time constant (τ). Over time τ msec, the voltage in a neuron will decrease by 1/e.
In very general terms, τ is usually about 10-100 msec. Taking the larger of those, a 100 mV change in membrane potential will decrease to 37 mV just 0.1 sec later and to 14 mV just 0.2 sec later. Voltage changes in neurons don’t hang around for very long.
What seems like a bug in neurons will be a feature, as we will see: this drop in voltage over distance and time is used to process information, especially in dendrites and cell bodies. The placement and timing of synaptic inputs to a neuron is critical for information processing.
Media Attributions
- Cable Theory Neuron RC Circuit © Michael Klausen is licensed under a CC BY-SA (Attribution ShareAlike) license

